圆中易错点分析

文 耿恒考（特级教师）

“圆”是初中数学的重要内容之一，也是许多同学学习的难点。由于对“圆”的认识、理解和掌握难度较大，因此，同学们在学习中应及时汇总自己的常错问题，精心选择有代表性的题目，通过细心分析归纳来化解难点。

一、忽略了点与圆的不同位置关系

例1平面内有一个⊙O和一点P，若点P到⊙O上的点的最大距离为8cm，最小距离为2cm，求⊙O的半径长。

【错因分析】对于这个问题，同学们更多的关注点在“点到圆上的最大距离和最小距离”上，无暇顾及点与圆的不同位置关系，往往只会考虑点P在圆外的一种情况，而忽略了点P在圆内的情形。

【正确解答】当点P在⊙O外时（如图1），直线PO交⊙O于点A、B，点P到⊙O上的点的最大距离PB=8cm，最小距离PA=2cm，所以⊙O的半径r=3cm；当点P在⊙O内时（如图2），直线PO交⊙O于点A、B，点P到⊙O上的点的最大距离PB=8cm，最小距离PA=2cm，所以⊙O的半径r=5cm。

图1

图2

二、忽略了一条弦所对的弧有两条、所对的圆周角有两组

例2如图3，AB是直径为8cm 的⊙O的一条弦，如果AB=4cm，那么弦AB所对的弧长为______，弦AB所对的圆周角为______°。

图3

【错因分析】同学们关注较多的是劣弧，往往忽略一条弦所对的弧有两条，且两条弧的和为一个圆周长；一条弦所对的圆周角有两组，且它们是互补关系。

【正确解答】⊙O中弦AB所对的劣弧长为，弦AB所对的优弧长为。⊙O中弦AB所对的圆周角为30°或150°。

三、忽略了弦与圆心的不同位置关系

例3已知，内直径为100cm 的下水管道的横截面是圆，截面圆中水面的宽度为80cm，求管道内水面的深度。

【错因分析】同学们的思维常将水面定位于圆心的下方（如图4），忽视了水面在圆心上方的情形（如图5）。

【正确解答】如图4、图5，过点O作OD⊥AB，垂足为点C，交⊙O于点D，则AC=BC=40cm。连接OA，根据勾股定理，得OC=。

图4

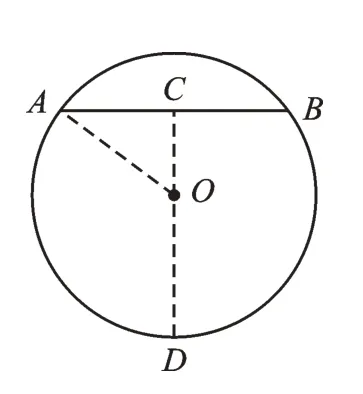
图5

当水面在圆心O的下方时，管道内水面的深度为50-30=20（cm）；

当水面在圆心O的上方时，管道内水面的深度为50+30=80（cm）。

例4已知，线段AB、CD是半径为5cm的⊙O中的两条弦，且AB∥CD，AB=6cm，CD=8cm，求两条弦AB、CD之间的距离。

【错因分析】对于这类问题，同学们习惯于关注两条平行弦在圆心同侧，忽略了两条平行弦在圆心异侧的情形，导致漏解。

【正确解答】如图6、图7，过点O作OE⊥AB，垂足为点E，交CD于点F，则OF⊥CD，则AE=3cm，CF=4cm。连接OA、OC，根据勾股定理，得3（cm）。

图6

图7

当平行弦AB、CD在圆心O的同侧时，弦AB、CD之间的距离为4-3=1（cm）；

当平行弦AB、CD在圆心O的异侧时，弦AB、CD之间的距离为4+3=7（cm）。

四、忽略了圆的轴对称性质

例5已知⊙O的半径为5cm，AB为直径，弦CD⊥AB，垂足为点E，CD=6，求AC的长。

【错因分析】对于这个问题，根据题意，同学们习惯于画出图8，而忽略了与之对称的图9。

图8

【正确解答】如图8，连接AC、OC。根据勾股定理，得OE=4cm，AE=5-4=1（cm）。在Rt△AEC中，由勾股定理得。如图9，连接AC、OC。根据勾股定理，得OE=4cm，AE=5+4=9（cm）。在Rt△AEC中，由勾股定理，得。

图9

本题也可以通过连接AC、OC、BC，利用相似三角形或射影定理来解决。