动中觅静 静中探解——四边形中动点问题的解题策略

文 谢丽丽

近几年，命题者常以四边形为背景，渗透点的运动，并对此点在运动变化过程中产生的等量、变量、图形间的关系进行考查。下面结合例题对四边形中的动点问题进行剖析，供同学们参考。

一、动点产生的分段函数

例1如图1，E为矩形ABCD的边AD上一点，点P从点B出发沿折线BE-D运动到点D停止，点Q从点B出发沿BC运动到点C停止，它们的运动速度都是1cm/s。现P、Q两点同时出发，设运动 时 间 为x（s），△BPQ的 面 积 为y（cm2），若y与x的对应关系如图2 所示，则矩形的面积是（ ）。

图1

A.96cm2B.84cm2

C.72cm2D.56cm2

【分析】我们先初步了解整个运动的过程，由于两点运动速度相同，那么可以厘清其中的三种情形：点P在线段BE上运动，点Q在线段BC上运动；点P在线段ED上运动，点Q在线段BC上运动；点P在线段ED上运动，点Q在点C处静止。明确三种情形的临界状态，再结合图像上的关键点进行分析，化动为静，便可将面积转化为线段长求解。

解：从函数的图像和点的运动过程可以得出，当点P运动到点E时，x=10，y=30。过点E作EH⊥BC，如图3。

图3

在Rt△BAE中，由勾股定理，得AE=8。

由图2知，当x=14时，点P与点D重合，即DE=14-10=4，

∴AD=AE+DE=8+4=12，

∴矩形的面积为12×6=72（cm2）。

故选C。

二、动点产生的图形

例2如图4，在矩形ABCD中，AB=1，，P为AD上一个动点，连接BP，线段BA与线段BQ关于BP所在的直线对称，连接PQ，当点P从点A运动到点D时，线段PQ在平面内扫过的面积为 。

图4

【分析】已知点P的运动轨迹是线段AD，因此，只需再确定点Q的运动轨迹即可。由轴对称得BQ=BA，而点B是定点，BA的长为定值1，所以点Q的运动轨迹是圆弧，其圆心角可结合已知数据求得。那么图5中的阴影面积即为所求，再利用分割法可求得面积。

解：∵线段BA与线段BQ关于BP所在的直线对称，

∴BQ=BA=1，△ABP≌△QBP。

∵点B是定点，

∴点Q的运动轨迹是以B为圆心的圆弧。

如图5，阴影部分即为当点P从点A运动到点D时，线段PQ在平面内扫过的图形。

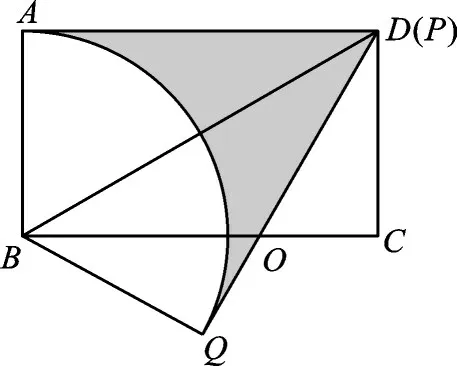
图5

三、动点产生的线段最值

例3如图6，在▱ABCD中，∠B=60°，AB=10，BC=8，点E为边AB上的一个动点，连接ED并延长至点F，使得DF，以EC、EF为邻边构造▱EFGC，连接EG，求EG的最小值。

图6

【分析】点E的运动带来▱EFGC的运动。▱EFGC中边的长度在变，但我们要抓住变化过程中不变的数量关系和位置关系，如EF=CG，EF∥CG。又由DF=。记CD与EG的交点是点O，由△DOE∽△COG，得。此时，问题转化为求线段EO长的最小值，即求两条平行线AB、CD之间的距离。

图7

四边形中的动点问题综合性强，常与圆、三角形等几何知识以及方程、函数等代数内容结合，要求较高。我们要抓住动点变化过程中不变的量，关注特殊四边形本身的数量关系和位置关系，必要时结合特殊状态或将相关线段代数化，通过动的现象寻觅静的本质，从动静间的转化出发剖析问题，实现动态问题静态化，最终实现问题的解决。