改进深度卷积神经网络及其在变工况滚动轴承故障诊断中的应用

张西宁,刘书语,余迪,雷建庚,李霖

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)

随着机械设备状态监测测量规模增大、测点数量的增多,机械设备状态监测和故障诊断进入了“大数据时代”[1]。传统的基于信号处理的故障诊断方法采用手动提取特征后输入分类模型进行故障识别[2],过程严重依赖人工经验和先验知识,这在数据规模大、获取速度快的今天显得捉襟见肘。如何从海量的机械大数据中自动提取有用特征,并精准地对轴承等零部件进行故障诊断成为当下研究热点。

深度学习因为处理数据和识别复杂问题能力强[3-4]受到了学术界和企业越来越多的关注。深度卷积神经网络(DCNN)是深度学习中最重要的模型之一,最早在20世纪80年代被提出,兴起于计算机视觉和自然语言处理等领域[5],如今被广泛应用在机械故障诊断领域。贾京龙等用卷积神经网络对变压器进行诊断并成功识别出故障[6];张伟等通过批量标准化和小批量训练的方法提高了卷积神经网络在多负载、强噪声环境下对轴承故障的识别能力[7];向宙等以卷积和池化后的特征为权值对反卷积核进行叠加,把信号逐层重构回原信号空间,通过观察重构信号,解释了卷积神经网络对信号提取的实质[8]。

深度卷积神经网络通过局部连接、权值共享和池化,不仅具有一定程度的平移不变性,还大大减少了网络的参数数量来避免过拟合[9]。常用的平均池化和最大池化都存在明显的缺点:平均池化是区域内每个活性值的权值相等,使得重要特征模糊化;最大池化只保留区域内的活性最大值,抛弃区域内其他神经元活性值的同时必然丢失大量的信息。针对这个问题,本文提出了一种用小尺度卷积核通过跳动的方式对特征进行降采样的方法。从神经元活性值与分布的角度[10],分析了提出的方法优于两种池化方式的原因,并在实验室变转速多轴承数据集上进行测试,对比了运用所提出池化方法的改进DCNN与其他两种DCNN在收敛速度、识别正确率和稳定性等方面的优势。

1 基础理论

1.1 深度卷积神经网络

深度卷积神经网络是参考生物学中感受野机制而提出的一种局部连接和权重共享的深度前馈神经网络[11]。典型深度卷积神经网络的结构如图1所示。卷积层的输入与输出关系的数学表达如下

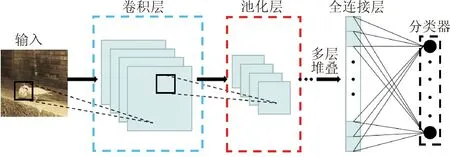
图1 典型深度卷积神经网络的结构Fig.1 Typical DCNN structure

Y=f(W*X+b)

(1)

式中:X∈RM×N×D和Y∈Rm×n×p分别为网络的输入和输出;W∈RU×V×P×D为卷积核;b为标量偏置;f(·)为非线性激活函数。池化层的作用是降低特征数量从而减少参数的数量,防止深度卷积神经网络过拟合。常用的池化层有最大池化层和平均池化层两种。

深度卷积神经网络通过误差反向传播对参数进行学习,计算卷积层和池化层的梯度后再通过链式求导法可以对整个网络的梯度传播进行计算。

损失函数L关于第l层的卷积核和偏置的偏导数为

(2)

(3)

式中:L为损失函数;W(l,p,d)为卷积核;Z(l,p)为第l层的第p个没经过非线性激活函数的净活性值;X(l-1,d)为第l-1层的输入;δ(l,p)为损失函数关于Z(l,p)的偏导数;b(l,p)为第l层的第p个偏置。

池化层由于没有权值,只需要计算损失函数关于池化层的输入神经元的导数。在进行最大池化时,正向传播只记录最大活性值所在的位置;反向传播只将梯度传递给记录下的神经元,其余神经元不参与传递。数学表达式如下

(4)

式中:al(i,t)为神经元;tm为正向传播时神经元最大活性值所在位置。

1.2 常用池化层的缺点分析

最大池化层是选择每个区域内所有神经元的最大活性值代表这个区域;平均池化层是对每个区域内所有神经元活性值取平均代表这个区域。最大池化和平均池化的数学表达式如下

(5)

(6)

式中:xi是区域Rk中每个神经元的活性值。

池化层虽然可以大幅度减少神经元的数量和参数量,但两种池化方式都存在比较明显的缺陷:平均池化是区域内每个活性值的权值相等,虽然综合考虑了区域内所有神经元活性值但会模糊重要的特征,效果通常不如最大池化好;最大池化操作假设越重要的特征活性值越大,因此只保留区域内神经元活性值的最大值,这种过于简单的选择方式,抛弃区域内其他神经元的活性值,必然会导致进行降采样的同时丢失图像大量的信息。

2 网络性能分析与改进

2.1 小尺度卷积池化

为了解决常用池化层的缺点,提出了用步长为2、激活函数为ReLU的小尺度卷积层代替最大池化层,对图片进行池化的策略。图像卷积层前后的输入、输出尺寸关系用数学公式可表示如下

N=[(Q-F+2P)/S]+1

(7)

式中:N为图像输出尺寸;Q为图像输入尺寸;F为卷积核尺寸;P为填充数量;S为卷积核滑动步长。

将卷积核的步长设置为2并不进行零补时,图像经过这样的卷积层后得到的输出尺寸变为输入尺寸的一半,起到和池化层一样的降采样效果。此外,这种池化方式可以使卷积核通过学习调整自身的权重,挑选有用的信息,既综合考虑区域内所有神经元的活性值,又能按每个神经元的重要程度分配不同的权重,使输出结果中蕴含着更多有用的信息,同时弥补了最大池化和平均池化的缺点。

小尺度卷积池化示意如图2所示。这种改进的池化方式因为含有激活函数增加了整个网络的非线性,提高了深度卷积神经网络的学习与表示能力。卷积操作会给网络引入更多需要学习的参数,对此引入3种策略平衡添加卷积操作导致参数大量增加的问题:首先选取引入参数相对较少的3×3小尺度卷积核;其次在最后用来池化的卷积层中使用深度可分离卷积核,对输入的每个通道分别执行空间卷积,然后通过逐点卷积将输出通道混合,需要的参数和计算量都少很多;最后用全局平均池化层代替平铺层和第一个全连接层。

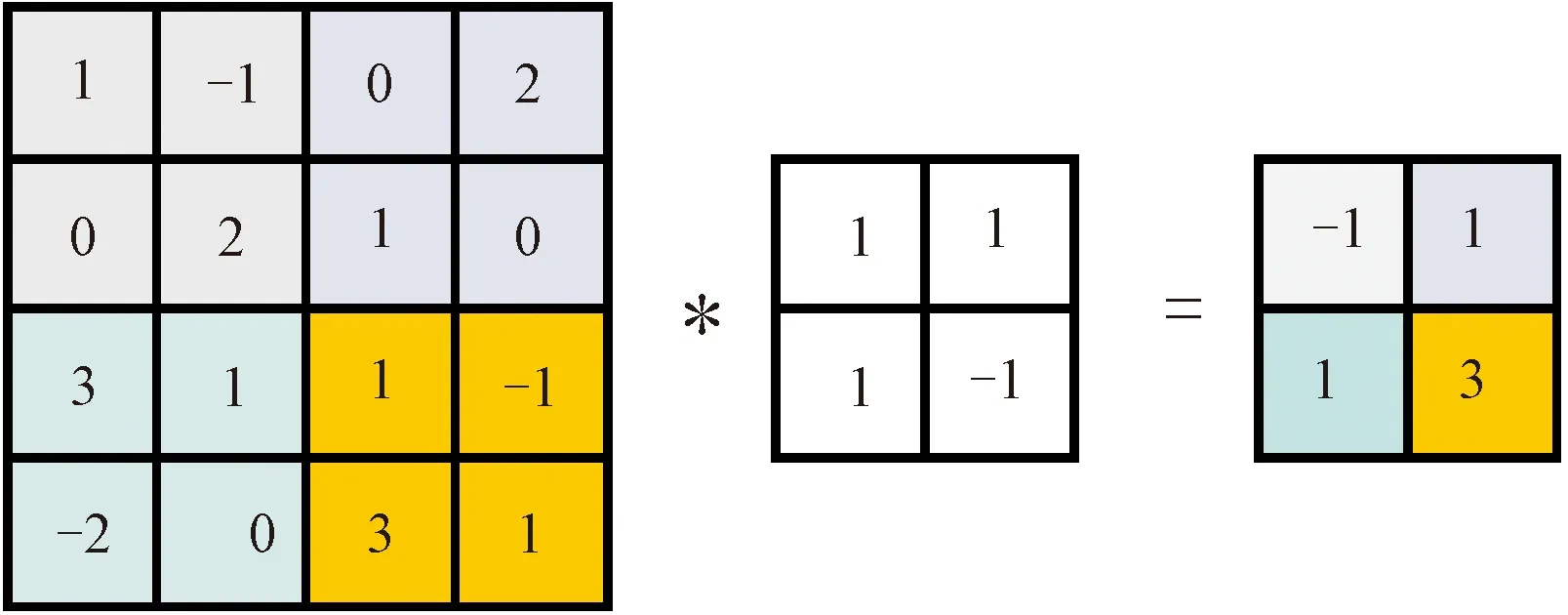
图2 小尺度卷积核池化示意图 Fig.2 Schematic diagram of small-scale convolutional pooling

2.2 小尺度卷积池化与最大池化分析与比较

为了分析提出的小尺度卷积池化性能优于最大池化的原因,将实验室中采集的变转速滚动轴承故障信号时频图输入到使用最大池化层的传统DCNN中,将网络中最大池化层可视化。经统计,传统DCNN每个最大池化层的通道总数与被激活通道的数量如表1所示。分析表1可以看出,输入传统DCNN中的图像在经过最大池化层时许多通道处于未激活的状态。

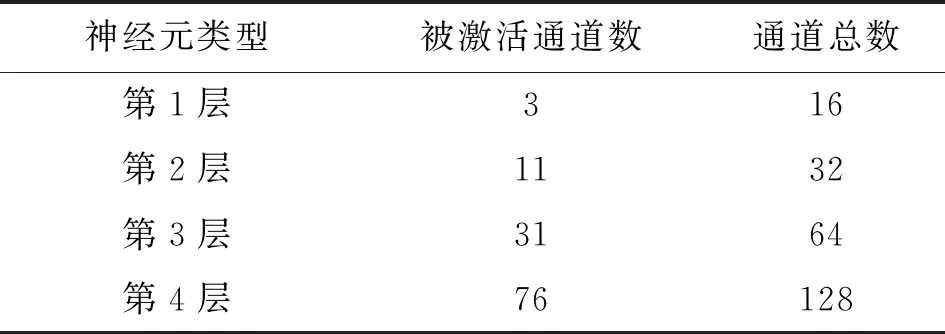
表1 传统DCNN最大池化层被激活通道数量Table 1 Number of activated channels in the maxpooling layers of traditional DCNN

对图像进行归一化,使像素缩放到[0,1]区间,然后输入到传统DCNN中统计最大池化层中神经元活性值的分布情况,如图3所示,以此分析最大池化层丢失大量信息的原因。从图中可以看出,最大池化层中神经元活性值大多集中在0附近,虽然活性值的分布随着网络深度的增加有扩展到[0,40]区间的趋势,但分布区间还是较小。把相同的时频图输入到使用小尺度卷积池化的改进DCNN中,对用来池化的卷积层进行可视化。统计改进DCNN各卷积池化层的总通道数与被激活通道的数量如表2所示。

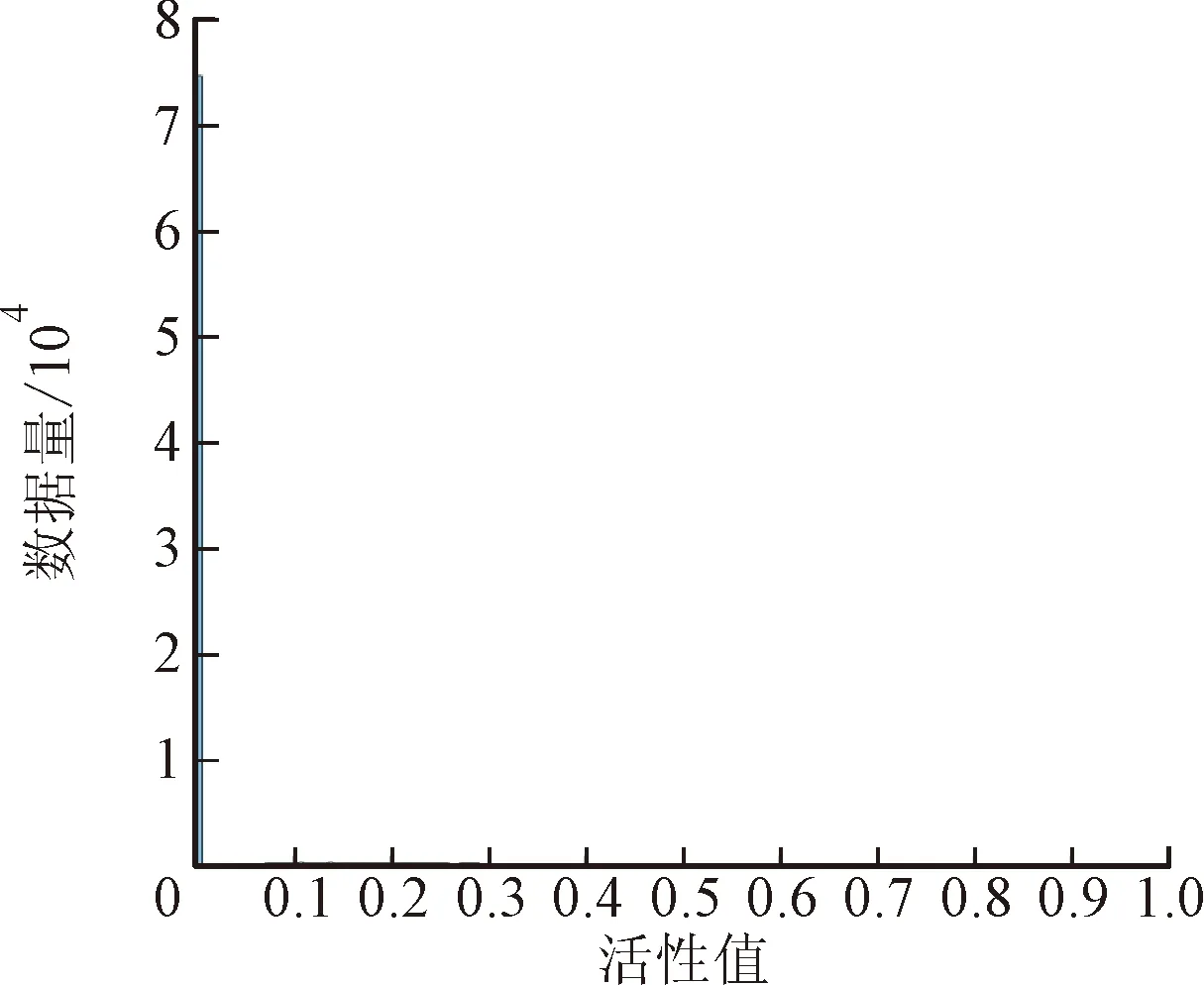
(a)第1层

对比表1和表2的数值可以看出,与传统DCNN相比,图像经过使用小尺度卷积池化的改进DCNN时,每个池化层中更多的通道处于激活状态,说明提出的池化方法更有效率。

表2 改进DCNN卷积池化层被激活通道数量Table 2 Number of activated channels in the convolutional pooling layers of improved DCNN

按照图3相同的方式,统计改进DCNN中卷积池化层神经元活性值的分布情况如图4所示。虽然多数神经元活性值仍集中在0附近,但活性值的分布区间更大,在第4层小尺度卷积池化层中,神经元活性值的范围扩展到了[0,120]。结合所用激活函数ReLU的图像可知,神经元活性值大于0时才处于激活状态。为证明提出的池化方法比最大池化在保留信息的数量与多样性上都存在优势,计算了两者激活的神经元占神经元总数的比例和神经元活性值的信息熵,计算结果如表3、表4所示。计算信息熵的公式如下所示

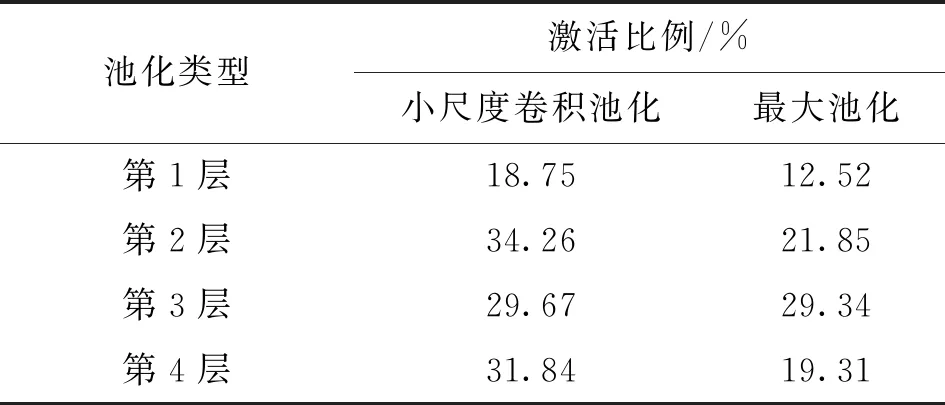
表3 两种池化方式神经元激活比例Table 3 Activation ratio of neurons in two pooling methods

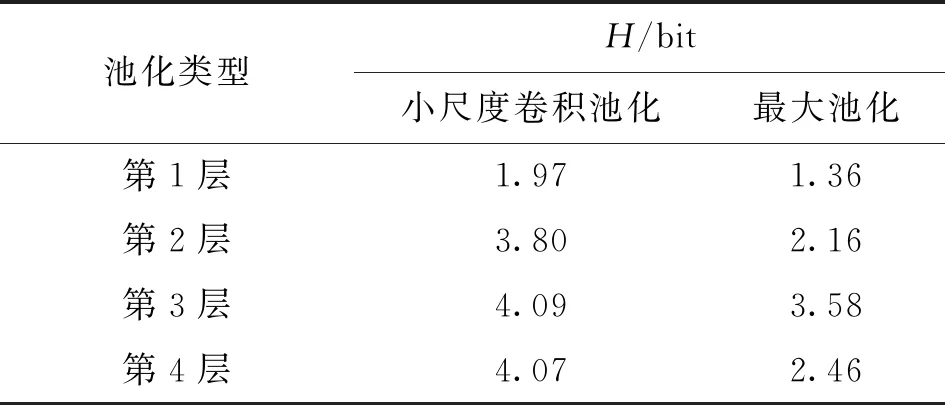
表4 两种池化方式神经元活性值的信息熵Table 4 Shannon entropy of the activity values of neurons in two pooling methods

(8)

式中:P(xi)为激活值xi的出现概率;n为不同激活值的数量。

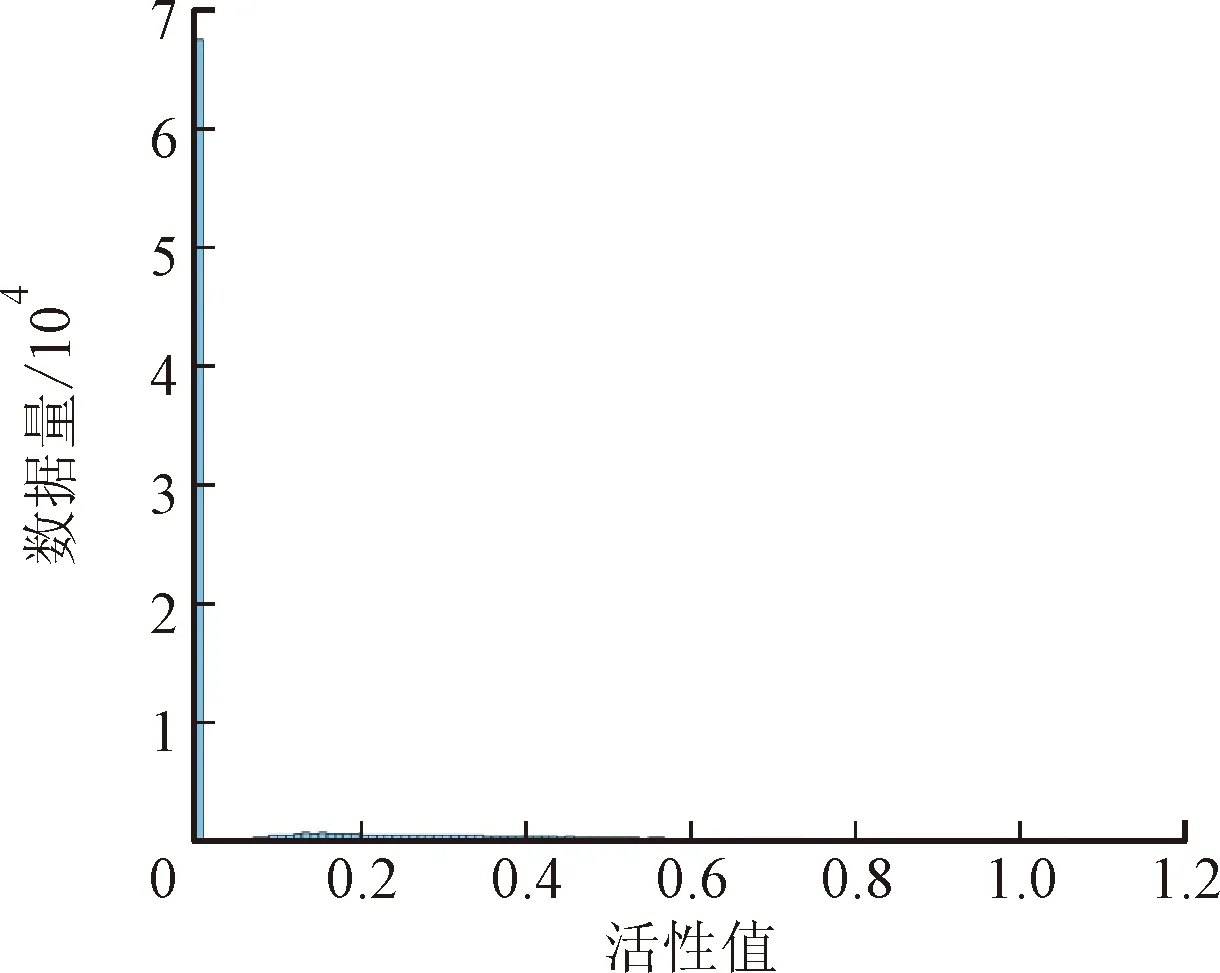
(a)第1层

分析表3、表4可以得知,每个小尺度卷积池化层被激活的神经元比例都比相应的最大池化层要高,而且神经元活性值的信息熵都有所增大。这种神经元活性值分布的多样性必然会蕴含着更丰富的信息,一定程度上解决了最大池化时丢失大量信息的缺点,有助于网络更全面的学习与表示。

3 改进DCNN变工况轴承故障诊断

为了验证提出的改进深度卷积神经网络的性能,在实验室采集了比较复杂的变转速滚动轴承故障信号。变转速下滚动轴承振动信号经常会发生调频、调幅和调相等现象[12],时域信号很难全面地反映信号中蕴含的复杂信息。时频分析可以把一维时域信号映射到二维时频平面上,全面反映出了变转速下采集到的非平稳信号时频联合特征。把采集的时域信号通过时频变换得到的时频图作为输入,通过深度卷积神经网络逐层进行特征提取与学习,可实现网络对变转速下轴承故障信号的识别与分类[13]。

如图6所示,实验室中的轴承实验台由直流电机、轴承安装座、加速度传感器、电涡流传感器、预紧装置、径向加载装置和数据采集卡UA300构成。加速度传感器灵敏度为8.8 pC/(m·s-2),频率测量范围是0.27～10 kHz;电涡流传感器灵敏度为8×10-3V/μm。

图5 轴承故障实验台实物图Fig.5 Picture of bearing experiment platform

3.1 实验室变转速数据集构成

实验中待测轴承为6308深沟球轴承,分为滚动体故障(B)、保持架故障(C)、内圈故障(I)、外圈故障(O)和正常(ZC)5种类别,每种类别包含4个轴承。实验过程中,手动调节直流电机的转速在200～2 400 r/min之间不均匀变化,径向加载7.7 kg的重物。每个类别的4个轴承各采2组信号,采样频率为10 240 Hz,采样时间为20 s,一共得到40组长度为204 800个点的信号。采集的40组信号中既包含升速过程也包含降速过程,通过相应的键向信号可以计算出轴承转速变化信息。由于深度学习需要大量的样本对网络进行训练,将40组信号分别从第1个点开始取连续的4 096个点作为一个样本,并且每隔2 048个点开始取下一个样本,样本的截取过程如图6所示。

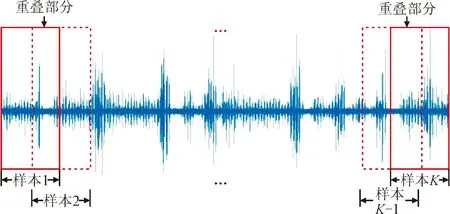
图6 截取时域信号示意图Fig.6 Schematic diagram of samples collection

每种类别获取了784个数据样本,总计3 920个数据样本。将数据样本分为训练集、验证集和测试集3个部分,其中数据样本数量分别为3 420、250、250。将数据样本进行连续小波变换,得到数据样本的时频图,不同小波基连续小波变换得到的时频图对于故障诊断结果存在一定的影响。根据文献[13-14]和实验结果对不同小波基连续小波变换进行对比,最终选择效果更佳的morlet小波基连续小波变换。保存时频图作为训练和测试深度卷积神经网络性能的数据集,数据集的组成情况如表5所示。

表5 实验室变转速数据集组成Table 5 Composition of variable speed datasets from laboratory

3.2 改进DCNN对变转速滚动轴承的故障诊断

将训练集的时频图像素归一化到区间[0,1]内,以输入150×150的初始尺寸搭建的改进DCNN进行训练,每经过一轮训练后用验证集来验证网络是否发生过拟合,待网络训练完成后将测试集输入网络中进行诊断和分类。实验使用的编程语言为Python 3.7.4,程序运行的环境为TensorFlow,使用计算机配置为Core i5-9500 CPU @ 3.00 GHz。改进DCNN的结构和详细参数如图7所示。

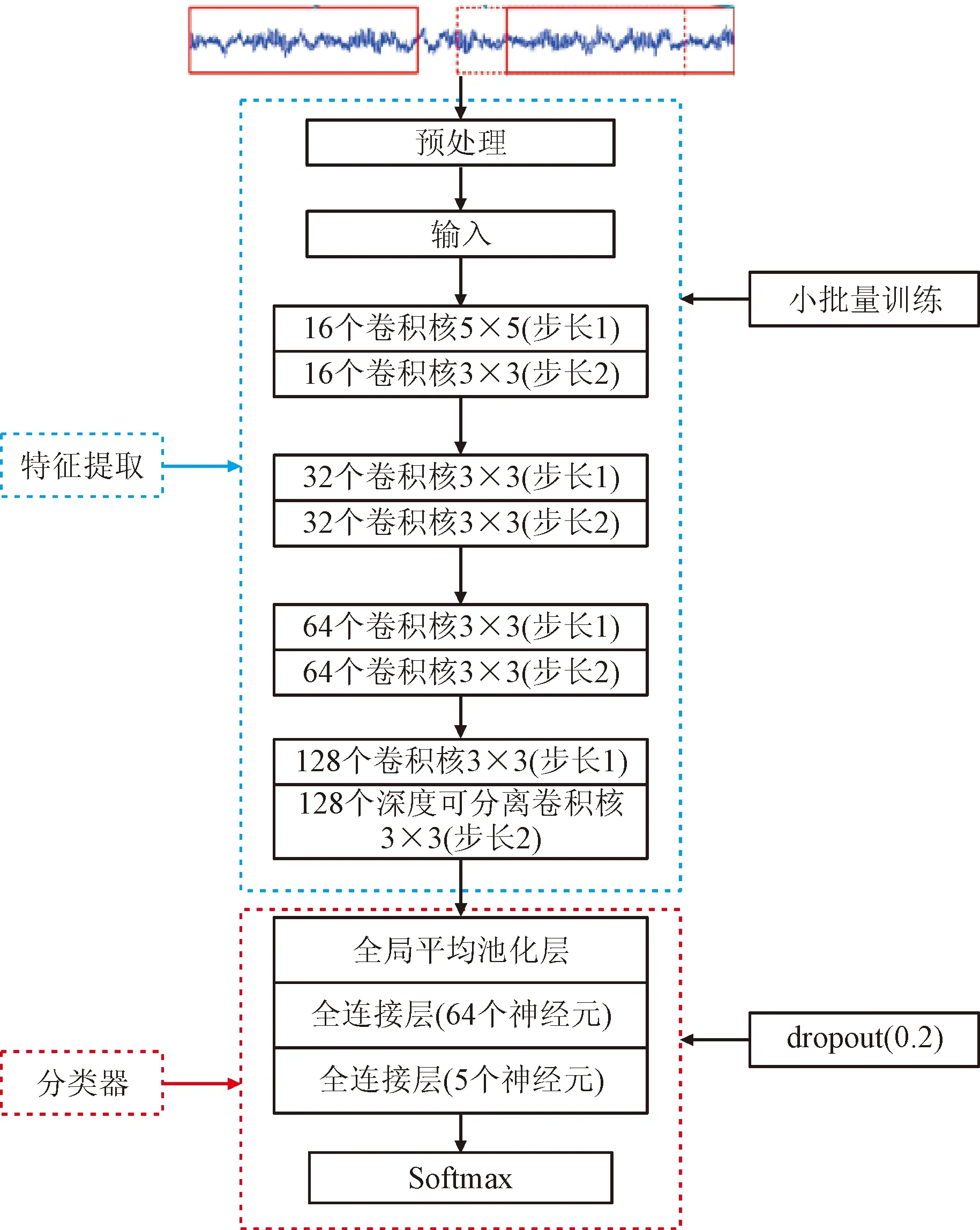
图7 改进DCNN结构和详细参数Fig.7 Improved DCNN structure and detailed parameters

网络第1层使用较大尺寸的卷积核可以提取时频图中较大视野的整体特征信息[7],后面的几层采用小卷积核可以提取时频图中较小的局部特征信息,也可以减少网络中需要训练的参数。为了减少网络中的过拟合现象,在训练网络时使用了小批量训练[7]和dropout技巧[15]。此外网络采用了分类交叉熵损失函数,并选择Adam[16]优化算法更新权值直到损失函数最小。将实验室变转速滚动轴承故障数据集分别输入没有改进的典型DCNN(DCNN-1)、使用最大池化的改进DCNN(DCNN-2)和使用小尺度卷积池化的改进DCNN(DCNN-3)。其中,DCNN-3的结构和详细参数和图7一致;DCNN-2是将DCNN-3所有小尺度卷积池化层改回传统的最大池化层,其余结构和参数完全一致;DCNN-1没有使用任何改进策略,是一个网络深度和参数与前面两个模型完全一致的典型DCNN模型。设置迭代次数为40进行20次实验,计算出3种网络测试集分类精度平均值和标准差如表6所示,各次实验测试集分类正确率变化曲线如图8所示。

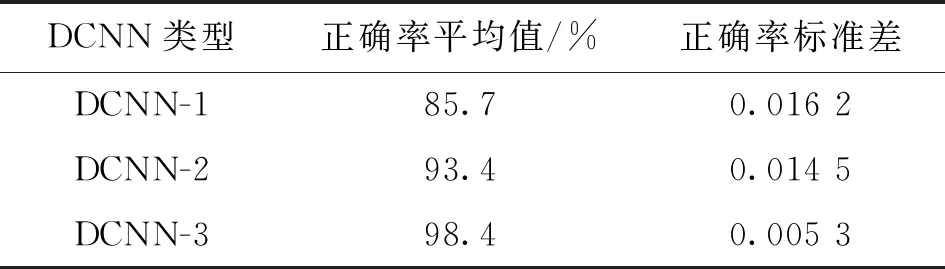
表6 测试集分类正确率的平均值与标准差Table 6 Mean and standard deviation of the recognition accuracy rates of the test set

结合表6与图8,对比DCNN-1和DCNN-2的结果可知,用全局平均池化层代替平铺层和第1个全连接层对DCNN进行改进后,网络的分类正确率从85.7%提升至93.4%,说明用全局平均池化代替平铺层和第1个全连接层改进的DCNN-2比典型DCNN-1具有更强的泛化能力,但网络的分类正确率和稳定性仍不够高。对比DCNN-2和DCNN-3的结果可知,在DCNN-2基础上使用小尺度卷积池化进行改进的DCNN-3将网络的分类正确率提升到了98.4%,标准差减小了63.4%,说明提出的池化方法使网络的性能和稳定性都进一步的提高。此外DCNN-2在第30次迭代时才开始收敛,而DCNN-3在第18次迭代时达到最大值并保持平稳。由于收敛速度快,DCNN-3的训练时间比DCNN-2减少了40%以上。为了定量验证使用小尺度卷积池化的DCNN-3比使用传统最大池化的DCNN-2提取特征的效果更好,计算网络最后一层的输出特征的类间距和类内距,结果如表7所示。类间距和类内距计算式如下

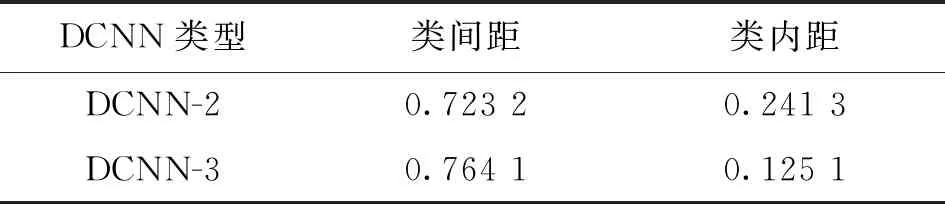
表7 DCNN-2和DCNN-3输出特征类间距和类内距Table 7 Intra-class distance and inter-class distance of output features of DCNN-2 and DCNN-3

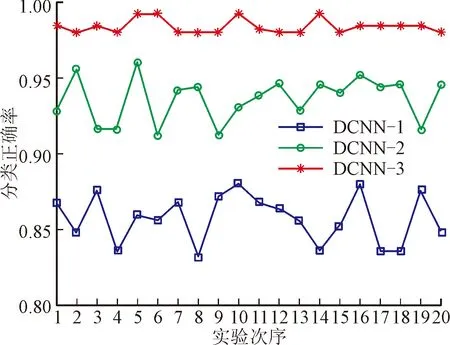
图8 3种网络测试集分类正确率对比 Fig.8 Comparison of recognition accuracy rates of 3 networks on the test set

(9)

(10)

式中:Ci为第i类样本的协方差矩阵;n为样本类别的数量;

tr为矩阵的迹;P(wi)为i类样本的数量占总体样本数量的比例;Mi和M0为第i类样本矩阵的均值和总体样本矩阵的均值。

从计算结果看出,使用小尺度卷积池化的DCNN-3提取的特征类间距比传统最大池化的DCNN-2大,类内距比DCNN-2小,再一次说明了使用小尺度卷积池化的DCNN-3性能更佳。

将使用小尺度卷积池化的DCNN-3对测试集故障分类结果表示成标准混淆矩阵,如图9所示。可以看出,5种类别的滚动轴承几乎无误地被分到正确的类别中,分类精度最低的内圈故障滚动轴承也能达到98%,说明本文提出的小尺度卷积池化DCNN-3在变转速滚动轴承故障被诊断中基本满足工程需求。

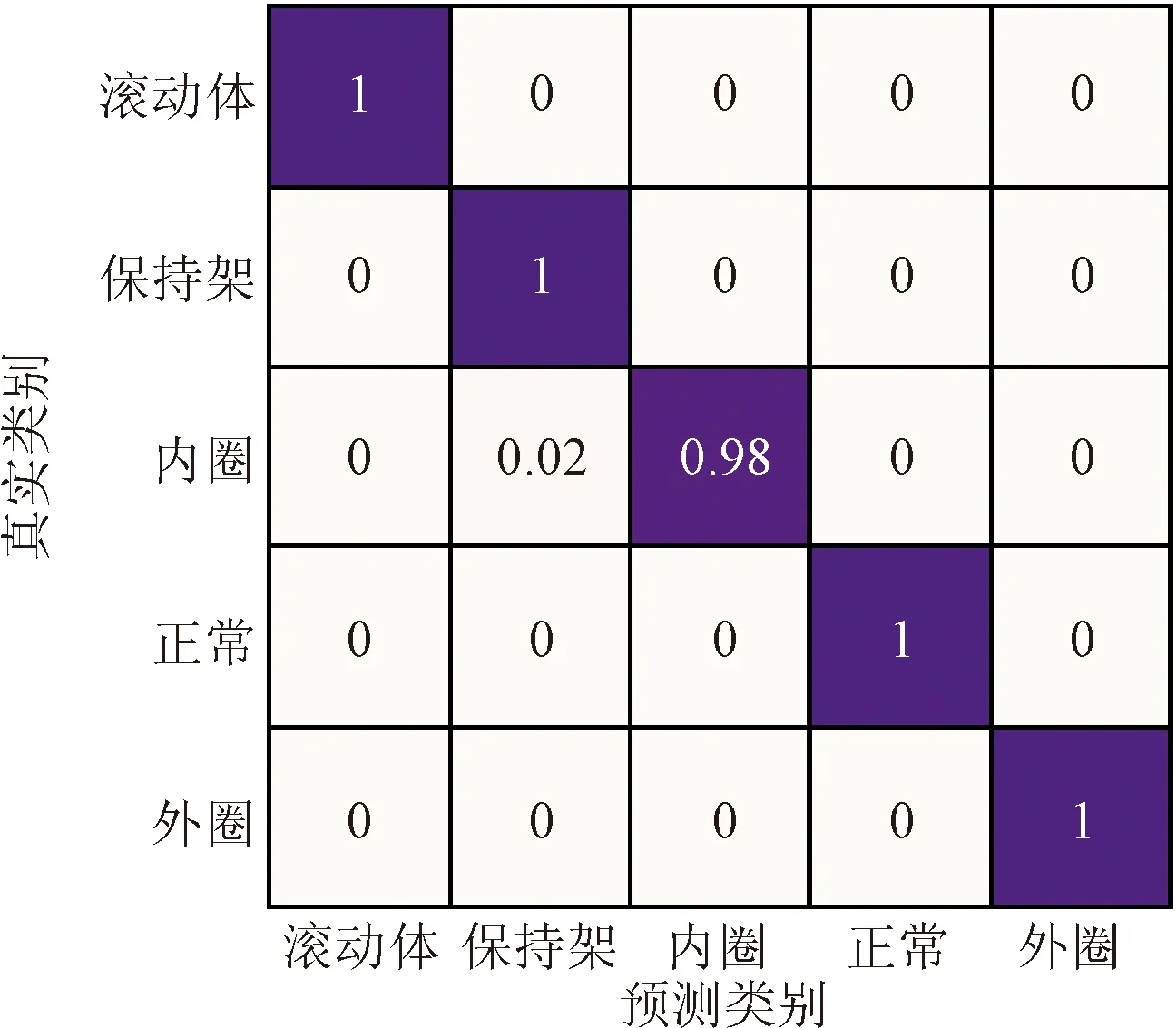
图9 故障分类结果标准混淆矩阵 Fig.9 Standard confusion matrix of fault classification results

4 结 论

为了解决两种常用池化方式的缺点,本文提出了一种用步长为2的小尺度卷积层代替常用池化层进行降采样的改进DCNN。运用改进DCNN和其他深度卷积神经网络在实验室变转速多轴承数据集上进行测试,得到结论如下。

(1)本文提出的方法相比最大池化有更多神经元处于激活状态,并且扩展了神经元活性值的区间。最后一个池化层神经元活性值的熵从2.46 bit提高到4.07 bit,增加了神经元活性值的多样性,完善了最大池化和平均池化的缺点。

(2)在变转速多轴承数据集上分别对使用了小尺度卷积池化的改进DCNN和其他深度卷积神经网络进行测试,结果表明,提出的改进DCNN不仅拥有更高的故障识别精度和稳定性,还将训练网络所用时间减少了40%以上。

(3)由提出的改进DCNN在测试集进行故障诊断的标准混淆矩阵观察到,5类滚动轴承均分到了正确的类别,说明提出的改进DCNN在变转速滚动轴承的故障诊断中基本满足工程需求。