基于高斯函数的池化算法

王宇航，周永霞，吴良武

（中国计量大学信息工程学院，杭州 310018）

0 引言

深度学习是Hinton 等［1］在2006 年提出的概念，指出深层网络训练采用无监督预训练初始化并用有监督训练微调网络权值的方法来解决梯度消失问题，在学术圈里引起了巨大的反响。自此深度学习进入高速发展阶段，并被应用到计算机视觉领域来处理图像分类、姿态估计、目标定位等问题。深度学习作为一类模式分析方法的统称，主要包括卷积神经网络（Convolutional Neural Network，CNN）、循环神经网络（Recurrent Neutral Network，RNN）和自动编码器（Auto Encoder，AE）三种方法，其中CNN 成为解决计算机视觉问题的主要方法。卷积神经网络主要由输入层、卷积层、池化层、全连接层、输出层等结构组成，由于网络结构设计的不同，不同的卷积神经网络的性能也有很大的差别。2012 年，Hinton和他的学 生Alex 设计出了AlexNet［2］，一举拿下了当年ImageNet 竞赛的冠 军。自此之后，诸如VGG（Visual Geometry Group）［3］、ResNet（Residual Network）［4］、GoogLeNet［5］、DenseNet（Densely Connected Networks）［6］等 更多更深的卷积神经网络模型被提出，极大推进了卷积神经网络的研究。

池化层在卷积神经网络中起到了至关重要的作用，它可以在一定程度上增加平移旋转的不变性。通过池化操作，卷积神经网络的感受野变大，这就有效降低了网络模型的优化难度［7］。常规的池化算法包括最大池化和平均池化，被广泛地运用到各种卷积神经网络之中，虽然发挥着很大的作用，但也有不足。为此，近年来科研人员提出了诸如随机池化、混合池化、光谱池化、模糊池化等池化算法。随机池化［8］根据池化域内每个元素的取值计算该点权重概率，并由此概率选取一个元素作为池化后的结果；混合池化［9］在最大池化和平均池化两种池化算法中随机选择一种作为当前池化层的池化算法，使得网络模型的泛化能力明显增强；光谱池化［10］运用离散傅里叶变换计算截断频域，进而实现降维操作，这种方法为每个参数保留了比其他池化算法更多的信息，因此效果显著；模糊池化［11］把模糊逻辑引入池化算法中，目的是解决传统池化算法中的选择不确定性，运用模糊逻辑中隶属度的计算方法，计算池化域的阈值，并由此确定池化结果；融合随机池化［12］在随机池化的基础上进行了改进，对池化域指定的范围使用随机池化算法，既考虑到了池化域内元素的平均值，又考虑到了池化域内元素的最大值。文献［13］中提出了一种基于信息熵的池化算法，首先介绍了熵池化的概念，然后根据熵池化提出分支熵加权算法，最后通过实验验证了该算法的有效性。soft 池化［14］以指数为基础，在池化算法中使用区域的激活函数softmax 的算子对池化域内每个元素进行权值运算，并加权求和作为算法计算结果，有效保留了特征图的细粒度信息，因此效果良好。

最大池化算法和平均池化算法由于计算方式简单，如果遇到池化域内元素值相差较大且不同元素点代表不同特征的情况时，很容易丢失部分特征信息。随机池化算法虽然引入概率计算的概念，但是最终仍然取池化域中一个元素为结果，这样可能会造成其他元素代表的特征被忽略。混合池化算法随机选择最大池化或平均池化作为池化方法，虽然增加了算法的泛化能力，但还是没有避免两种池化算法的弊端。光谱池化算法运用离散傅里叶变换把池化域里的元素从时域转换为频域进行处理，然后通过傅里叶反变换把结果转换到时域，虽然可以保留更多特征信息，但是运算过程繁琐复杂，大幅增加了算法的时间复杂度和空间复杂度。模糊池化算法依靠模糊逻辑解决池化域元素不确定性的问题，虽然有些效果，但是模糊逻辑过于依赖隶属度函数的选择，针对不同类型的卷积神经网络以及不同数据集可能需要使用不同的隶属度函数才能取得较好的效果，这就导致了该算法的泛化能力较差。融合随机池化算法对随机池化算法做了改进，对池化域内指定区域随机池化运算，但是本质上还是随机池化运算，倘若区域选择不当，位于两个区域边界的元素包含的特征信息依旧有可能被忽略，所以该方法只是一定程度上解决了特征信息丢失的问题，并没办法完全避免该问题。基于信息熵的池化算法选择信息熵作为度量方法，在池化域较大、元素信息较多时确实可以取得理想的结果，但是当池化域较小、元素信息较少时，该算法较其他算法在运算结果方面并无明显差别，运算效率却低下许多。soft 池化虽然可以保留特征图中大部分信息，但是由于该算法本身是可微的，反向传播时要进行梯度运算，所以较其他算法在性能方面会稍逊一筹。

1 基于高斯函数的池化算法

众所周知，池化操作本质其实是下采样，卷积神经网络中引入池化层是为了压缩输入的特征图，降低神经网络计算时的算法复杂度。但是在这个过程中，如果池化算法选择不当，有可能会造成原有输入的特征图里的部分特征信息丢失，进而影响整个卷积神经网络的效果。

由于池化域内所有元素的值本质上可以被看作是一组一维的数据，本文受机器学习中最近邻（K-Nearest Neighbors，KNN）算法中近邻（相似）程度概念的启发，提出池化域内各元素点与该池化域所含主要特征之间关联性的概念。所谓各元素点与该池化域所含特征之间的关联性，即同一池化域内不同元素点与该池化域内所包含的最突出的特征（一般认为是池化域内所有元素点的最大值）的相关密切程度。KNN 算法中以待决策样本与已知样本的距离作为依据来判断近邻程度，本文提出的各元素点与该池化域所含主要特征之间的密切程度的判断方法与其类似：首先找到该池化域内所有元素点的最大值作为已知样本；然后计算该池化域内所有元素点的值到该样本的距离；最后根据得到的距离衡量该元素点与该池化域所含主要特征之间的关联性。由此可知，同一池化域内，某个元素点的值与该池化域内所有元素点中的最大值距离越接近，则认为该元素点与该池化域内所包含的最突出的特征相关程度越密切，关联性越强，那么这个元素点越重要；反之，该元素点与该池化域内所包含的最突出的特征相关程度越疏远，关联性越弱，那么这个元素点越不重要。

在进行池化计算时，如果可以考虑到池化域内各元素点与该池化域所含主要特征之间的关联性，根据池化域内每个元素关联性的强弱来计算池化后的结果，便可以尽可能地保留输入特征图的特征信息，提高卷积神经网络的性能。诸如最大池化、平均池化、随机池化等大多数传统的池化算法虽然能起到一定的效果，但是由于算法本身较为简单，计算过程中并未很好地考虑到池化域内各元素点与该池化域所含特征之间的关联性，所以难免会在一定程度上丢失特征信息。鉴于这种情况，本文受概率学中高斯分布的相关知识启发，提出一种基于高斯函数的池化算法：通过借用高斯函数来计算和衡量池化域内各元素与其所含主要特征之间的关联性，并由此作为依据计算池化算法的结果。

1.1 高斯函数

高斯函数是德国数学家Johann Carl Friedrich Gauss 在1795 年提出的一种初等函数。高斯函数在自然科学中有着极大的影响力，被广泛地应用于数学、统计学、计算机学等多门学科之中。本文以高斯函数为基础，提出了一种新的池化算法。高斯函数的解析式如式（1）所示：

其中：参数a、b、c均为常数。

从式（1）可以看出参数a影响了高斯函数的峰值大小；参数b决定了高斯函数曲线对称轴的位置；参数c决定了高斯函数曲线的曲率，即c越大、曲线越平缓，c越小、曲线越陡峭。

1.2 算法原理

1.2.1 前向传播

本文算法通过引入高斯函数来表示池化域内各元素与该池化域所含特征之间的关联性。具体做法为：计算池化域内每一个元素的高斯函数值，并定义该函数值为该元素的高斯权重。由前文叙述可知，计算得出的高斯权重可以在一定程度上衡量池化域内各元素的关联性。

对于高斯函数的参数，本文定义参数a恒等于1；由前文叙述可知，本文使用高斯函数的目的是衡量池化域内各元素与其最突出特征的关联程度，高斯函数的计算结果正比于输入值到参数b的距离，所以定义参数b为池化域内特征最突出点的值，即所有元素的最大值；参数c为根据参数b计算得到的标准差。参数b和参数c具体计算公式如式（2）和式（3）所示：

其中：N为池化域内元素个数，xi为池化域内第i个元素。

如果池化域内所有元素都相同，即xi=b，虽然根据式（3）计算的参数c为0 使得式（1）毫无意义，但是此时池化域内所有元素相等，所有元素的高斯权重自然也相等，所以定义此时f(x；a，b，c)=1。因此，本文使用的高斯函数计算公式如式（4）所示：

根据高斯权重，对于池化域内各元素进行加权平均计算，并将最终计算结果作为本文算法的输出值，加权平均计算的公式如式（5）所示：

其中：N为池化域内元素的个数，fi为池化域内第i个元素的高斯权重，xi为池化域内第i个元素，y为加权平均计算的结果。

综上所述，基于高斯函数的池化算法的运算步骤如下：

1）取池化域内所有元素的最大值为参数b。

2）将池化域内元素代入式（3）计算，求得参数c。

3）将参数a、b和c代入式（4）求取每个元素的高斯权重。

4）根据各元素的高斯权重，由式（5）对各元素进行加权平均计算。

具体算法流程示例如图1 所示（图中池化域尺寸为2×2，步长为2，计算结果保留两位小数）。

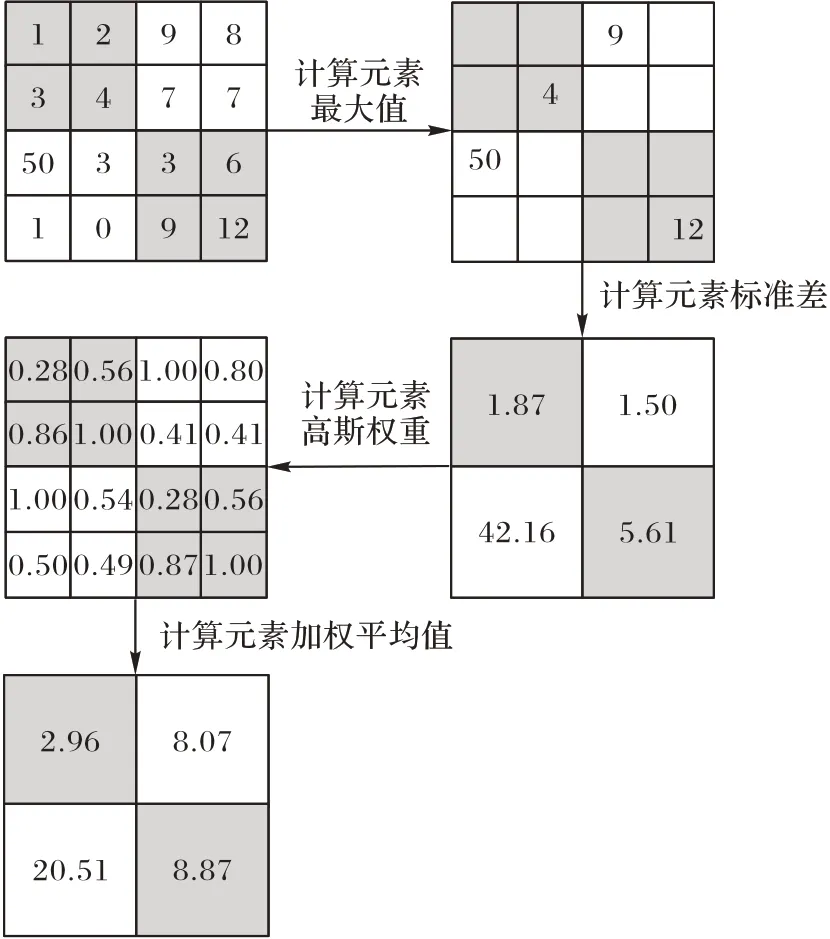
图1 算法流程示例图Fig.1 Example of algorithm flow

1.2.2 反向传播

反向传播是训练卷积神经网络最为常用的一种方法，其原理是根据由损失函数计算出的误差信息，运用某种优化算法对各神经元的权重进行优化。一般来说，反向传播分成计算各权重的偏导数和更新权重两步。由于池化层只是减少了输入矩阵的元素个数，并没有需要更新的权重，所以对于池化层来说，反向传播只需要将后一层计算得到的梯度数量扩大到前一层需要的梯度数量，然后将这些梯度传递给前一层网络即可。

本文提出的池化算法在常规算法的基础上通过在各元素里引入高斯权重，并且最后使用加权平均法减少池化域内元素的个数，所以反向传播时只需要根据高斯权重逆推导这个过程即可，计算公式如式（6）所示：

其中：fi为池化域内第i个元素的高斯权重，N为池化域内元素的个数，x为后一层网络计算得出的梯度值，yi为池化域内需要传递给前一层网络的第i个元素的值。该算法的流程如图2 所示。

图2 反向传播算法流程Fig.2 Flowchart of back propagation algorithm

1.2.3 时间复杂度

由前文叙述可知，本文算法计算步骤分为计算参数b、计算参数c、计算池化域内各元素高斯权重和计算加权平均值4 步。由式（2）可知，计算参数b实质上是求取池化域内元素的最大值，其时间复杂度为O(n)；由式（3）可知，计算参数c实质上是求取池化域内各元素与参数b的标准差，其时间复杂度为O(n)；由式（4）可知，计算池化域内各元素高斯权重的时间复杂度为O(n)；由式（5）可知，加权平均运算的时间复杂度为O(n)。由于本文算法的4 个计算步骤时间复杂度均为O(n)，且计算方式为串行计算，故算法的时间复杂度为O(n)。

2 实验及其结果与分析

2.1 实验模型

LeNet5 是Lecun 等［15］在1998 年提出的用于手写体字符识别的卷积神经网络模型。它共由8 层组成，分别为输入层、C1 卷积层、S2 池化层、C3 卷积层、S4 池化层、C5 卷积层、F6 全连接层和输出层。LeNet5 的模型结构如图3 所示。

图3 LeNet5模型结构Fig.3 Structure of LeNet5 model

VGG16 是牛津大学计算机视觉实验室2014 年提出的网络结构。它由13 层卷积层、5 层池化层以及3 层全连接层组成。VGG16 的网络模型结构如图4 所示。

图4 VGG16模型结构Fig.4 Structure of VGG16 model

ResNet［4］是由He 等在2015年提出的卷积神经网络模型。ResNet18 由1 层卷积层、1 层池化层、4 个残差块和1 层全连接层组成，其中每个残差块包含两层卷积和一条直连通道。残差块结构如图5 所示。

图5 残差块结构Fig.5 Structure of residual block

2019 年，谷歌通过继承前两代轻量级神经网络使用的深度可分离卷积技术和倒残差结构，并且结合资源受限的神经网络架构搜索技术和NetAdapt 算法提出第三代轻量级神经网络——MobileNet v3。MobileNet v3 分为Large 和Small 两个版本，两个版本的基本结构相似，区别仅在于网络大小不同。本文选取MobileNet v3 Small 为实验模型，该版本的网络结构如表1 所示。

表1 MobileNet v3 Small模型结构Tab.1 Structure of MobileNet v3 Small model

为验证基于高斯函数的池化算法的效果，本文将LeNet5、VGG16、ResNet18 和MobileNet v3 Small 中原有的池化算法分别替换为最大池化、平均池化、随机池化、混合池化、模糊池化、融合随机池化、soft 池化和基于高斯函数的池化，将替换得到的32 个模型作为实验模型。

2.2 实验数据集

本文选用CIFAR-10、Fer2013 和GTSRB（German Traffic Sign Recognition Benchmark）三个公开数据集进行实验。

CIFAR-10 数据集［16］是一个经典的图像分类数据集，包括60 000 幅像素为32×32 的彩色图像，其中50 000 幅图像用于训练，10 000 幅图像用于验证，无测试集。该数据集中的图像共分为airplane、automobile、bird 等10 个类别，每个类别6 000 幅图像，所有类别均是完全互斥的，且不同类别间特征大不相同，所以常常被用于验证图像分类算法的性能。

Fer2013 数据集由Carrier 和Courville 创建［17］，是国际机器学习会议2013 面部表情挑战赛所使用的数据集。它由35 887 幅48×48 像素的人脸表情灰度图构成，其中训练集、验证集和测试集的图像数量分别为28 709、3 589 和3 589。该数据集将表情分为愤怒、厌恶、害怕、高兴、悲伤、惊讶、中性7 类，每类表情对应图像数量并不均衡，并且每张图像的拍摄角度、背景、人物年龄等都不相同，这些因素极大增加了分类难度，要求图像分类算法具有很好的泛化性和鲁棒性才能取得较好的效果。

GTSRB 数据集是国际神经网络联合会议举办的多级图像分类挑战赛所使用的数据集之一［18］。该数据集中共有51 839 幅图像（其中训练集39 209 幅、验证集12 630 幅、无测试集），涵盖43 种不同的交通标识，每种标识为一种类别，不同类别包含图像数量不一，且图片质量参差不齐，识别难度要大于其他交通标识分类数据集。

2.3 实验结果与分析

2.3.1 CIFAR-10数据集实验结果

本节实验使用CIFAR-10 数据集，设置训练batch size 为256、学习率为0.001、优化器为Adam、损失函数为交叉熵损失函数、Epoch 为60，分别取第20、40 和60 个epoch 时的top-1（精确到小数点后三位）为模型性能评估指标。实验结果如表2 所示。

表2 各模型在CIFAR-10数据集上的top-1指标 单位：%Tab.2 Top-1 index of each model on CIFAR-10 dataset unit：%

从表2 中可以看出，在CIFAR-10 数据集上，本文提出的池化算法适用于各个模型上的top-1 较其他7 种池化算法的top-1 提高了0.5～6 个百分点。

2.3.2 Fer2013数据集实验结果

本节实验使用Fer2013 数据集，设置训练batch size 为256、学习率为0.001、优化器为Adam、损失函数为交叉熵损失函数、Epoch 为30，分别取第10、20 和30 个epoch 时的top-1（精确到小数点后三位）为模型性能评估指标。实验结果如表3 所示。

表3 各模型在Fer2013数据集上的top-1指标 单位：%Tab.3 Top-1 index of each model on Fer2013 dataset unit：%

从表3 中可以看出，在Fer2013 数据集上，本文提出的池化算法适用于各个模型上的top-1 较其他7 种池化算法的top-1 提高了1～5 个百分点。

2.3.3 GTSRB数据集实验结果

本节实验使用GTSRB 数据集，设置训练batch size 为256、学习率为0.001、优化器为Adam、损失函数为交叉熵损失函数、Epoch 为15，分别取第5、10 和15 个epoch 时的top-1（精确到小数点后三位）为模型性能评估指标。实验结果如表4 所示。

从表4 中可以看出，在GTSRB 数据集上，本文提出的池化算法适用于各个模型上的top-1 较其他7 种池化算法的top-1 提高了0.5～3 个百分点。

表4 各模型在GTSRB数据集上的top-1指标Tab.4 Top-1 index of each model on GTSRB dataset

2.3.4 运算时间对比实验结果

本节实验选取分辨率分别为100×100、1 000×1 000 和10 000×10 000，像素点为0～255 随机数的图片各10 幅，将这些图片作为最大池化、平均池化、随机池化、混合池化、模糊池化、融合随机池化、soft 池化和基于高斯函数的池化八种池化算法的输入，统计各池化算法的运行时间作为实验结果。

上述各池化算法的均池化域为2×2，步长为2。为避免实验结果具有偶然性，本节实验以各组图片10 次实验结果的平均值（单位为ms，保留3 位小数）作为最终实验结果，如表5 所示。

从表5 中可以看出，相比最大池化、平均池化和混合池化等传统池化算法，本文提出的池化算法由于计算量大一些，所以运算时间较长；本文算法虽然有一定的计算量，但是相比其他较为新颖的池化算法，本文算法的计算过程并没有特别复杂，所以运算效率方面优于这些算法。

表5 各算法在不同图片分辨率下的运行时间 单位：msTab.5 Running time of each algorithm under different image resolution unit：ms

2.3.5 实验结果分析

由表2～4 中的实验结果可知，无论是在LeNet5 模型、VGG16 模型、ResNet18 模型还是MobileNet v3 模型上，本文提出的基于高斯函数的池化算法对比最大池化、平均池化、随机池化、混合池化、模糊池化、融合随机池化和soft 池化七种池化算法在CIFAR-10、Fer2013 和GTSRB 三个数据集上精度方面都有不同程度的提升，这说明该算法在不同的模型和数据集上都具有一定的适用性。

由表5 中的实验结果可知，本文提出的基于高斯函数的池化算法相比最大池化在运算效率方面虽然不及一些传统算法，但相较于其余新颖算法也有所提升，这说明本文算法适用于可以适当降低对性能的要求，但对精度要求较高的场景。

3 结语

本文根据卷积神经网络池化算法研究现状，发现现有的池化算法大都没能很好地考虑池化域内各元素与该池化域所含特征之间的关联性，于是提出了一种基于高斯函数的池化算法，并且详细介绍了该算法的原理、前向传播和反向传播的流程。

本文选择LeNet5 模型、VGG16 模型、ResNet18 模型和MobileNet v3 模型作为实验模型，分别在CIFAR-10、Fer2013和GTSRB 三个公开数据集上进行实验，并且记录不同训练次数时模型的top-1 作为实验结果。实验结果表明：对比其他池化算法，本文提出的池化算法在不同的模型和数据集上均取得了不错的效果；本文还选择不同分辨率的图片对算法运行时间进行实验，实验结果表明：本文提出的池化算法在运算效率方面表现尚可。

综上所述，得出结论：文中提出的基于高斯函数的池化算法具有可行性和泛化能力，可以用于不同情况的理论研究和应用场景中。