电机伺服系统快速自适应抗扰控制
方靖荃,邓文翔,姚建勇,陈久辉,王鹏飞
(南京理工大学机械工程学院,210094,南京)
电机伺服系统在工业和国防领域有着广泛应用,因此其高精度运动控制问题一直是相关领域的研究热点[1-3]。然而,由于实际系统存在诸多模型不确定性,包括参数不确定性[4]和未建模干扰[5](如非线性摩擦等),严重制约系统控制性能的提升,给电机伺服系统的高精度运动控制带来巨大挑战[6]。
为解决上述问题,研究者们提出了各种不同的控制策略。Whitaker等人提出的自适应控制(AC)通过参数自适应律实现未知参数的在线更新,可以有效处理系统参数不确定性[7-8]。Yao等人提出的自适应鲁棒控制(ARC),能够同时处理系统参数不确定性与未建模干扰,在理论上保证了给定的瞬态跟踪性能和稳态跟踪精度,并且当仅存在参数不确定性时,还可以实现渐近跟踪[9-10]。当系统未建模干扰较强时,ARC只能通过高反馈增益保证良好的控制效果,然而过高的反馈增益可能激发系统高频动态进而引发系统失稳。Han等人提出的自抗扰控制(ADRC)利用扩张状态观测器(ESO)对广义扰动进行估计,实现在不需要太多系统模型信息的条件下的干扰补偿[11-13]。然而,ADRC未精确考虑系统的参数不确定性,当系统模型不确定性主要来自不确定参数时,其控制性能往往弱于传统自适应控制。文献[14-15]融合自适应控制和基于干扰观测的补偿控制的特点,提出了一种基于模型的自抗扰自适应控制方法(ADRAC)。ADRAC控制器在保留所融合的两种控制方法优势的同时,克服了它们各自的性能缺陷,但由于该控制策略中参数自适应律仅由跟踪误差和系统状态估计误差驱动,参数估计收敛速度较慢,进而导致了较差的系统瞬态跟踪性能。
基于以上考虑,本文针对实际电机伺服系统,提出了一种快速自适应抗扰控制(FADRC)方法。考虑到未知参数和其估值间的误差一般难以测量,通过引入一阶低通滤波运算和辅助中间变量提取参数估计误差,构造了一种由跟踪误差、参数估计误差及状态估计误差复合驱动的新型参数自适应律,并与扩张状态观测器有效融合,实现系统未知参数估计指数收敛的同时可主动补偿系统的未建模干扰。当系统存在时变干扰时,所提出的控制方法可保证一致最终有界的跟踪性能,当系统只存在常值干扰时,还可获得优异的渐近跟踪性能。此外,得益于新型快速参数自适应律,系统的瞬态性能可以获得有效提升。针对电机伺服系统的测试实验验证了本文所提出控制方法的有效性以及相比于现有方法的优越性。
1 数学建模
本文研究的伺服电机系统体系结构如图1所示:位移控制器接收参考位置信号x1d(t)并将控制输入u传递至电机驱动器,外部编码器向位移控制器反馈电机位置信号构成位置闭环;运行于转矩模式下的驱动器驱动永磁同步电机带动惯性负载,驱动器内部的PID控制器完成电流闭环。控制器设计目标为:给定x1d(t),设计一个有界且连续的u使得系统输出位移x1跟踪x1d(t)的误差尽可能地小。考虑到电机的电磁时间常数相较机械时间常数小得多,并且电流环的响应速度远大于位置环的响应速度,故可忽略电流环动态,将其近似为比例环节处理。可建立惯性负载的动力学方程如下

图1 电机伺服系统体系结构图Fig.1 Architecture diagram of motor servo system
(1)
式中:y和m分别表示角位移和负载惯量;Ki表示力矩常数;u表示控制输入;B表示黏性摩擦系数;f表示其他未建模干扰,如非线性摩擦、外干扰等。
(2)
为了便于控制器设计,作如下假设。
假设1系统参考位置信号x1d(t)二阶连续可微,且其各阶导数均有界。
假设2未知参数θ的范围已知,即
θ∈Ωθ≡{θ:θmin≤θ≤θmax}
(3)
式中:θmin=[θ1min,θ2min]T、θmax=[θ1max,θ2max]T分别表示未知参数的已知下界和上界。
2 快速自适应抗扰控制器设计
针对电机伺服系统,本文提出的快速自适应抗扰控制(FADRC)方法的原理如图2所示。一方面,通过设计参数自适应律降低系统参数不确定性;另一方面,通过构造扩张状态观测器估计系统未建模干扰。在此基础上综合考虑,设计控制输入u。

图2 快速自适应抗扰控制系统框图Fig.2 Block diagram of fast adaptive disturbance rejection control system
2.1 参数自适应律设计
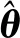
(4)
式中:Si代表向量S的第i个元素(i=1,2)。
采用如下参数自适应律
(5)
式中:Γ>0为对角自适应率矩阵;τ为自适应律函数。对于任意的自适应律函数τ,所使用的不连续投影映射均可以保证[9]
(6)
2.2 扩张状态观测器设计
根据文献[16],可构造系统扩张状态观测器(ESO)如下
(7)

情形1令x3≡d(x,t),则基于系统模型可构造系统扩张状态方程如下
(8)
式中:h(t)表示x3关于时间的导数。
系统状态估计误差动态可表示为
(9)

(10)

(11)
系统状态估计误差动态变为
(12)
由于矩阵A是Hurwitz矩阵,故一定存在正定矩阵J满足如下Lyapunov等式
ATJ+JA=-E
(13)
式中E表示单位矩阵。
通过计算不难求出矩阵J

(14)
经过分析可以发现,无论如何定义系统的扩张状态变量,所构造的ESO都是相同的,不同的只是状态估计误差动态的表达式。这一性质将有助于在不同情形下运用Lyapunov函数进行稳定性分析。此外,基于文献[17]的结论可以推断,所构造的线性ESO是稳定的,且理论上通过增大参数ωo,可以保证系统的状态估计误差任意小。
2.3 控制器设计
由反步法思想,设计快速自适应抗扰控制器的步骤如下。
步骤1定义如下误差变量
(15)
式中:z1为系统跟踪误差;α1为状态x2的虚拟控制律;z2为两者之间的偏差。
对z1求导,可得
(16)
设计虚拟控制律如下
(17)
式中增益系数k1>0。由式(15)~(17)可得
(18)
步骤2设计第二通道的自适应律。为了便于理论推导,在情形1(即x3≡d(x,t))的条件下,假设系统的未建模干扰为常值,即h(t)=0,将式(2)中的第2个公式变形为
(19)

(20)
式中,k>0表示滤波运算系数。
另外,注意到
(21)

进一步,可定义如下辅助中间变量P、Q
(22)
式中l为滤波系数,是一个正值常数。
对上式进行积分操作,可得P、Q表达式如下
(23)
由上式可推得
Q=Pθ
(24)
进而可定义包含参数估计误差信息的矩阵H
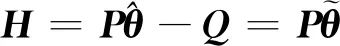
(25)
定义λmax(·)和λmin(·)分别表示相应矩阵的最大最小特征值,则有如下引理。
引理1如果回归矩阵φ满足持续激励条件(PE),则矩阵P是正定的,使得其最小特征值λmin(P(t))可以满足[18]
(26)
式中σ为常数。
在此基础上,可定义参数自适应函数τ为
(27)
式中C1>0、C2>0、C3>0表示自适应增益系数。
不同于传统控制方法的自适应律,式(27)提出的新型参数自适应律包含3项:第1项φTz2基于系统跟踪误差信息,第2项PTH/‖H‖基于参数估计误差信息,第3项εTJB1φ/ωo基于系统状态估计误差信息。当取定系数C2=0时,式(27)退化为自抗扰自适应控制所采用的自适应律;进一步取定C3=0,则退化为传统自适应控制对应的经典自适应律。
通过运用新型参数自适应律,可以在继承传统自适应律优点的基础上,克服其参数估计收敛速度较慢,系统瞬态跟踪性能较差等缺点,进而帮助改善控制性能。
基于获得的参数估计值,设计实际的控制输入u为
(28)
式中:k2>0为增益系数;ua是基于在线参数估计和系统状态估计进行调整的模型补偿项;us是线性鲁棒反馈项,用来保证系统鲁棒性。
3 稳定性分析及证明
对于由式(2)描述的电机伺服系统,所设计的快速自适应抗扰控制器(28)及参数自适应律(27)可保证如下有关系统稳定性的结论。
结论1当h(t)=0时,闭环系统所有信号均有界,且跟踪误差渐近收敛至0。
结论2当h(t)≠0时,闭环系统所有信号均有界。
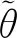
基于Lyapunov稳定性理论,结合所提出的电机伺服系统快速自适应抗扰控制(FADRC)方法,对以上稳定性结论逐条进行证明。
结论1证明在情形1的条件下,可定义Lyapunov函数如下
0.5C3εTJε
(29)
将式(8)、式(15)~(17)及式(27)代入上式,同时假设h(t)=0,对上式求导可得
0.5C3ωo‖ε‖2
(30)
定义
Z=[z1,z2,ε1,ε2,ε3]T
(31)
Λ1=
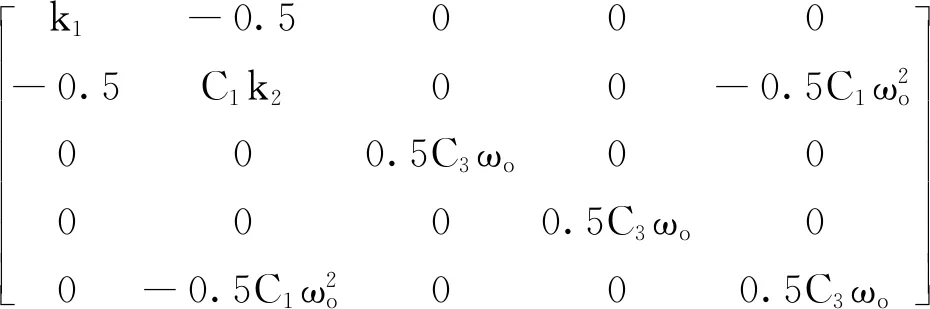
(32)
可通过调整参数k1、k2、C1、C2、C3、ωo使得对称矩阵Λ1正定,因此可得
(33)
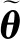
结论2证明当未建模干扰项d(x,t)为时变的函数时,运用情形2来进行分析。此时假设h(t)有界(即|h(t)|≤ζ,ζ>0),可定义Lyapunov函数如下
V2=0.5z12+0.5C1z22+0.5C3εTJε
(34)
类似于上文的处理,对上式求导可得
0.5C3(ωo-1)‖ε‖2+C3η
(35)
式中,η定义为
(36)
定义
(37)
可通过调整参数k1、k2、C1、C2、C3、ωo,使得对称矩阵Λ2为正定,则可得
(38)
对式(38)积分可得
(39)
由以上推导可知,对于该闭环系统而言,所有的信号都是有界的,系统的跟踪误差z1有界稳定,结论2得证。

(40)
对式(40)求导可得
(C1‖φ‖|z2|+C2‖ε‖‖JB1‖‖φ‖/ωo)]
(41)
由于z2→0且φ是有界的,所以存在某一时刻tf>0,当t>tf时有
(C1‖φ‖|z2|+C2‖ε‖‖JB1‖‖φ‖/ωo)<
0.5C3σ
(42)
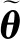

(1)k1、k2、ωo和C1、C2、C3偏小会影响控制效果且可能导致矩阵Λ1,Λ2的不正定,偏大又会因为测量噪声和高频动态等因素导致系统不稳定、控制效果恶化。因此,通常从较小的初值开始谨慎地增加以提高跟踪性能,直至达到满意的效果。

(3)自适应矩阵Γ、滤波运算增益系数l、k主要影响系统参数自适应过程的速度和效果。一般而言,较小的k和较大的Γ有助于使得参数估计值收敛得更快更平稳。在此基础上,通过反复试错法完成参数调试取值。
4 实验验证
4.1 电动伺服实验平台搭建
为了验证所设计的FADRC控制器的控制性能,搭建电动伺服实验平台以进行不同工况下的实验验证对比。该实验平台包含实验系统、测控系统两部分,实验系统主体由支座、伺服电机和负载惯量盘组成,电机主轴与负载之间通过联轴器连接,并配有角度编码器和扭矩传感器。测控系统由控制柜、显示屏和鼠标键盘组成,控制柜内包含一台搭载Ardence RTX7.0实时操作系统的工控机,A/D转换板卡和D/A转换板卡,光电编码器数据采集卡、电源以及电机驱动器等。下位机控制程序在实时操作系统的基础上由离散化的C++代码编写,并通过LabWindows CVI构建了相应的上位机可视化监控软件,系统的控制采样周期设定为0.5 ms。

图3 电动伺服实验平台Fig.3 Electric servo experiment platform
电动伺服实验平台各关键元件具体型号规格见表1。

表1 关键元件型号规格Table 1 Types of key components
4.2 对比实验及分析
通过在如下4种控制器间进行比较,验证所设计的控制器的有效性和优越性。
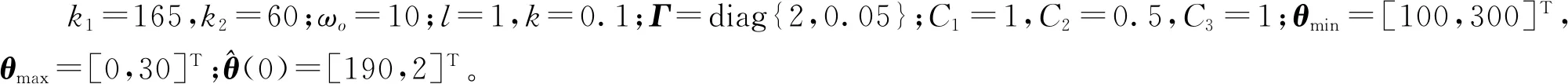
传统自抗扰自适应控制器ADRAC,其参数自适应律不包含参数估计误差信息,故调整C2=0,其他参数与FADRC一致。
经典自适应控制器ARC,其参数自适应律仅包含跟踪误差信息,且该算法不含扩张状态观测器。故取ωo=0,C2=0,C3=0,其他参数不变。
自抗扰鲁棒控制器RCESO与FADRC相比,该控制器不含参数自适应,故取控制输入u表达式内参数项为其名义值即可,其余不变。
为了充分验证控制器的控制性能,实验验证环节分为无干扰和有干扰两种工况。
(1)无干扰工况。参考位置信号为x1d(t)=10sin(0.5πt),此工况下不同控制器的跟踪误差对比如图4所示。

图4 4种控制器在无干扰工况下的跟踪误差对比Fig.4 Tracking errors under non-interference condition
为了量化实验数据,借鉴文献[15],在表2中选取跟踪误差的最大值Me、平均值μ和标准差σ这3项指标以衡量不同控制器的控制性能。

表2 无干扰工况下的性能指标Table 2 Performance indexes under non-interference condition
对比表2数据可知,由于ADRAC控制器有效融合参数自适应律和扩张状态观测器,相较于单纯的自抗扰控制器(RCESO)和自适应控制器(ARC),各项性能指标均有所提高;在此基础上,FADRC同时考虑了跟踪误差、系统状态估计误差和参数估计误差,优化了系统参数估计收敛速度和瞬态性能,跟踪精度进一步提升,稳态误差峰值缩小至0.033 2°,较ADRAC减小约13.8%。
图5为2种控制器在无干扰工况下的参数估计对比。由数据分析可知,ADRAC控制器参数估计收敛耗时约25 s,本文设计的FADRC控制器仅用时约5 s,这是由于引入包含参数估计误差信息的切换项,因而使得参数估计快速收敛,相较于ADRAC控制器参数估计速度提升约80%,充分证明了系统快速性的特点。
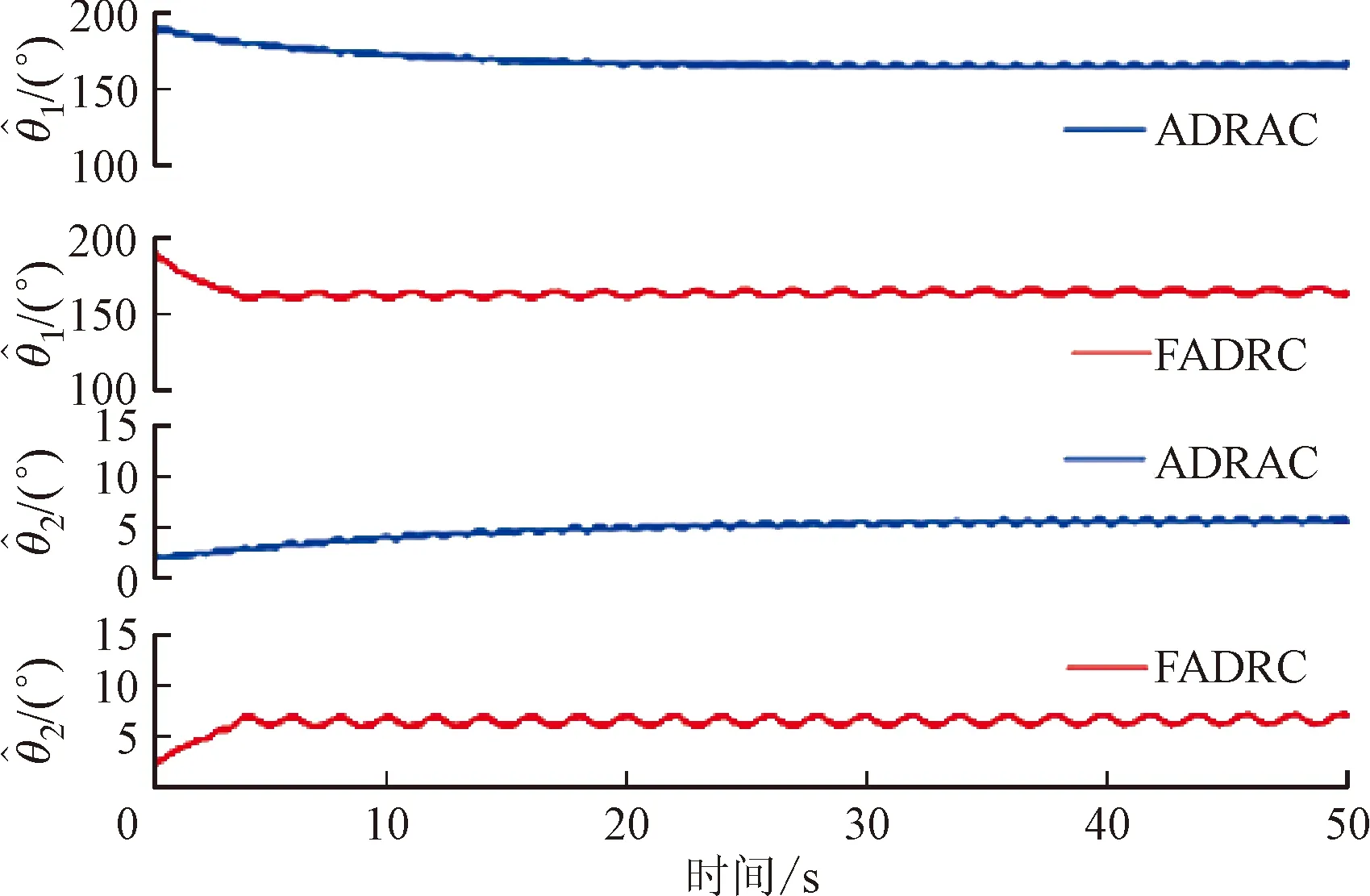
图5 无干扰工况下的参数估计Fig.5 Parameter estimation under non-interference condition
(2)有干扰工况。该工况下参考位置信号不变,干扰是通过修改D/A板卡的控制输出函数ur来模拟实现的。为了充分验证所设计控制方法的抗扰性能,将ur修改为ur=u-0.05x1-0.05x2,式中x1,x2分别为位置干扰项和速度干扰项。
各控制器在该工况下的跟踪误差对比如图6所示,量化数据列于表3中。

图6 4种控制器在有干扰工况下的跟踪误差对比Fig.6 Tracking errors under interference condition

表3 有干扰工况下的性能指标Table 3 Performance indexes under interference condition
分析数据可知,当存在位置-速度干扰时,FADRC控制器性能指标虽然较无干扰工况有退化,如图7所示。这是由于参数估计快速收敛,减轻了ESO的估计负担[14],与其他控制器相比仍具有较好的控制精度,证明了FADRC自身具有良好的抗扰性能。

图7 有干扰工况下扩张状态观测 Fig.7 Expanded state observation under interference conditions
综上所述,本文所设计的FADRC控制器,相较于其他传统控制器,在位置跟踪的稳态误差和在线参数估计的收敛速度等方面都有明显改善,具有更为理想的控制性能,充分验证了其有效性和相比于现有控制方法的优越性。
5 结 论
本文提出了一种电机伺服系统的快速自适应抗扰控制(FADRC)方法。所设计的控制器融合了自适应控制和基于干扰观测器的补偿控制,分别处理参数不确定性和未建模干扰,保留了两种控制方法的优势的同时,克服了它们的性能缺陷。所设计的参数自适应律中不仅包含跟踪误差项、系统状态估计误差项,还引入了与参数估计误差有关的切换项,显著提升了系统控制的稳态精度和在线参数估计的收敛速度,改善了系统控制性能。利用Lyapunov方法分析了闭环系统的稳定性,并通过实验结果对比验证了所提出的控制器的有效性和优越性。

