平行轴纯滚动内啮合线齿轮设计方法

何迪,何恩义,殷诗浩,吴海华,杜义贤,叶喜葱

(三峡大学机械与动力学院,443002,湖北宜昌)

传统工业齿轮由于齿廓形状复杂,微小化和微纳化应用都十分困难[1-2]。2007年,陈扬枝等提出了空间曲线啮合理论,通过空间曲线构造“简单实体”替代传统齿轮以空间复杂曲面构造的三维“复杂实体”,实现了齿轮占用空间的最小化设计[3-4]。如图1所示,早期线齿轮以钩杆和圆柱基体组成悬臂梁结构,应用于轻载条件下的传动装置。近年来,许多学者开展了基于空间曲线啮合的齿轮设计研究。陈扬枝等推导了斜交轴和交错轴线齿轮的基本设计公式并构建了线齿轮样本[5-6],在后续工作中,通过实验验证了传动的平稳性和连续性。陈兵奎等建立了沿任意接触角方向的啮合方程等式,并提出用等距包络法构建管状齿面[7-8]。姚莉等提出了一种满足常规动力传递的线齿轮设计方法,并研究了基于四轴加工中心的线齿轮加工技术[9-10]。陈祯等提出了根据啮合线函数来主动设计共轭曲线,并介绍了圆柱齿轮[11]、相交轴齿轮[12]和齿轮齿条[13]的几何设计、啮合性能和机械性能。上述的研究主要集中在外啮合传动领域,针对内啮合线齿轮的研究较少,导致现阶段线齿轮机构在轮系装置的应用受到限制。

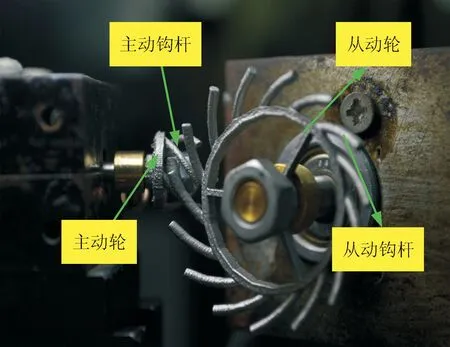
图1 线齿轮样件[4]Fig.1 Sample of line gear

在齿廓啮合时,由于接触点的速度大小和方向不同会导致齿廓之间存在相对滑动,造成齿面磨损、节点冲击和噪声等不利因素[14]。为了削弱相对滑动带来的负面影响,早在20世纪初,Grant提出使齿顶高趋近于0,仅通过轴向重合来确保传动的连续性,使两齿轮仅在节点处啮合以实现纯滚动啮合。由于传递动力微乎其微,中心距稍大便会脱啮,故未得到实际应用。黄锡恺团队提出,一对纯滚齿廓应只在节点接触、在齿轮的其他旋转位置均不接触,纯滚动齿廓应位于渐开线等共轭齿廓曲线内部,并找到多种简单实用的纯滚齿廓曲线,研制出了系统的纯滚齿轮[15-16]。宜亚丽等基于五次多项式类曲线的无刚、柔性冲击等特点,设计了激波器齿形,实现纯滚动活齿任意齿差等速共轭传动[17]。谭儒龙等研究了纯滚动接触的摆线锥齿轮,并通过现有面滚齿工艺加工样品进行实验,使用纯滚动摆线锥齿轮的齿轮箱可以实现更高的传输效率[18]。

为了扩展线齿轮的啮合传动形式,减小齿廓相对滑动的负面影响,本文基于空间曲线啮合理论,研究一种平行轴纯滚动内啮合线齿轮机构。分析了内啮合线齿轮纯滚动啮合的条件,并构建了3种接触形式的齿面数学模型。根据数学模型,构建线齿轮副实体模型,并验证线齿轮副的传动平稳性。

1 建立共轭接触线

建立空间右手坐标系,如图2所示。E为线齿轮副安装中心距,夹具坐标系O-x0y0z0、O-xpypzp记为S0和Sp。与小齿轮、齿圈固连的坐标系O-x1y1z1、O-x2y2z2记为S1和S2。啮合的初始时刻,与S0和Sp重合。小齿轮和齿圈分别以角速度ω1、ω2绕z0、zp轴匀速运动,其转向相同,经过t步长,转动角度为θ1和θ2。在啮合过程,空间曲线R1和R2的始终保持点接触。通过坐标变换和相关参数可得到S1到S2的变换矩阵

图2 空间坐标系Fig.2 Space coordinate system

M21=M2pMp0M01=

(1)

小齿轮接触线R1在坐标系S1下,参数方程为

(2)

式中:t为空间曲线的变参数;te、ts分别表示接触线进入啮合点和退出啮合点的变参数对应值。上标表示矢量所在的坐标系。

假设空间曲线R1和R2在任意啮合时刻的接触点为N(x1,y1,z1),则相对速度υ12在坐标系S1的表达式[19]为

(3)

式中:E为O1到O2的矢量,它的模为线齿轮副中心距E。方程中的各个矢量在S1中可表示为

(4)

由空间曲线啮合理论[3],可得一对共轭曲线在任意点的啮合方程为

(5)

式中:β为小齿轮、齿圈上接触线在接触点N的主法失,可通过下式计算

(6)

由式(5)可解得转角θ与t之间的关系

θ1=f(t);i21=θ2/θ1

(7)

根据式(1)(5)和(6),得到小齿轮接触线R2在坐标系S2下的参数方程为

(8)

为了可以得到在啮合过程没有相对滑动的一对共轭曲线,需要保证在啮合过程中任意啮合点的相对速度为0,即

(9)

由式(4)可知,在任意啮合时刻,啮合点N的相对速度在S1中可表示为

(10)

通过式(1)～(10),可以得到纯滚动内啮合平行轴线齿轮副的一对共轭曲线。

2 纯滚动齿面构建

2.1 齿面方程

以接触线R1、R2上的点做为坐标原点、夹具坐标系S、Sp的基矢量作为x、y、z轴,建立齿廓坐标系OS-xsecyseczsec、OS-xsec2ysec2zsec2(简写为δ1、δ2)。在啮合点N处,小齿轮和齿圈的齿廓截面如图3所示,r1、r2分别为小齿轮和齿圈的齿廓截面圆弧半径;γ是OSN与xsec轴形成的接触角,决定接触点N在圆弧上的位置。当接触点落于A、B处时,会存在边缘接触。为减少边缘接触,提高齿轮的接触强度,建议将接触点设置在圆弧AB中点附近。

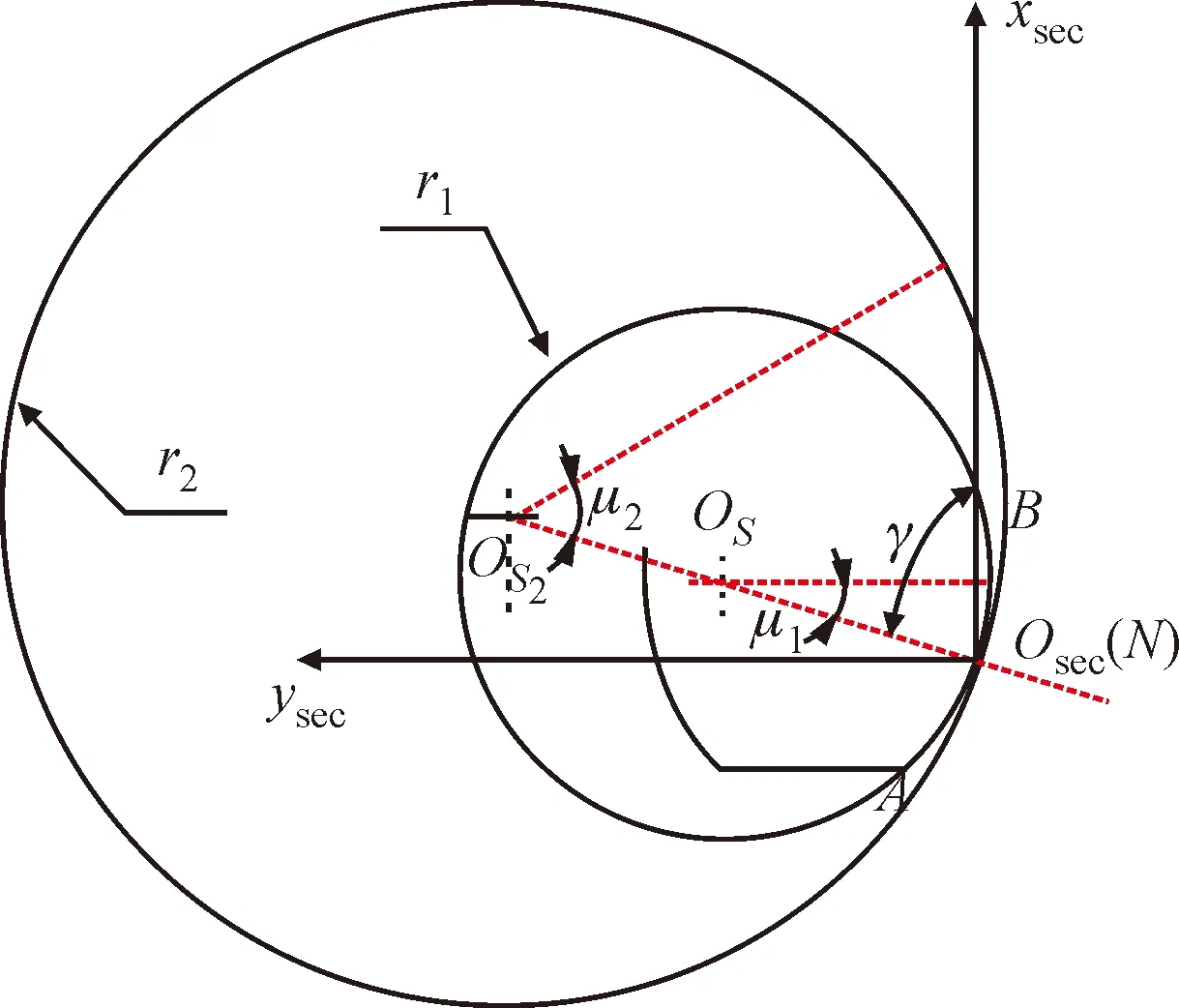
图3 齿廓截面圆弧Fig.3 The circular arc of profile cross-section

小齿轮、齿圈的齿廓截面曲线在坐标系δ1、δ2下的参数方程分别为

(11)

(12)

式中:μ1、μ2为齿廓截面曲线方程的变参数。以小齿轮齿廓截面曲线内侧为正方向,当齿圈齿廓截面曲线的圆心OS2在OS同侧时,式(12)取正号;反之,取负号。符号会影响构建齿面的凹凸性,下文将详细讨论。

如图4所示,圆弧齿面是由齿廓截面曲线沿轴向的螺旋运动形成,其齿面方程可表示为

图4 齿面接触线和圆弧截面关系示意图Fig.4 Schematic diagram of the relationship between contact curve on tooth surface and arc section

(13)

式中:i=1,2时,式(13)分别表示小齿轮齿面和齿圈齿面;MSi-δi是齿廓坐标系δi到坐标系Si的变换矩阵。

2.2 齿面构建

2.1节中,齿廓截面曲线方程中正负号的选择不同,会影响齿面凹凸性。根据小齿轮和齿圈齿廓截面曲线的圆心位置和圆弧半径r1、r2,可以构建出3种不同接触形式的啮合齿面:凸凹接触、凸凸接触和凸平接触。本文选取小齿轮齿廓截面曲线方程正号为例。

(1)凸凹接触。当式(11)取正号、式(12)取正号时,小齿轮和齿圈的齿廓截面圆弧的圆心OS、OS2位于同侧。此时,齿圈齿面为凹齿面,接触类型为凸凹接触,如图5所示。

图5 凸凹接触Fig.5 Convex-concave contact

(2)凸凸接触。当式(11)取正号、式(12)取负号时,小齿轮和齿圈的齿廓圆弧的圆心OS、OS2位于异侧。此时,齿圈齿面为凸齿面,接触类型为凸凸接触,如图6所示。

图6 凸凸接触Fig.6 Convex-convex contact

(3)凸平接触。当式(11)取正号、式(12)取负号且ρ2→∞时,圆弧AB演变为直线AB,齿圈齿面变为切平面,此时接触类型为凸平接触,如图7所示。

图7 凸平接触Fig.7 Convex-flat contact

对于3种接触形式的齿面,由于接触点的相对曲率半径不同,其齿面接触应力也不相同。由赫兹接触原理[20-21]可知,啮合点的接触应力计算公式为

(14)

式中:qmax为最大接触应力;Q为外力;E1、E2分别为小齿轮和齿圈材料的弹性模量;ν1、ν2为泊松比;Σr为相对曲率半径;“+”表示凸齿面对凸齿面的接触形式;“-”表示凸齿面对凹齿面的接触形式。

由式(14)可知,在相同载荷条件下,齿面接触应力与相对曲率半径成反比。凸凹接触的齿面相对曲率半径最大,接触应力最小。假设E1=E2=2×105MPa,ν1=ν2=0.3,Q=20 N,r1=1 mm,r2=4 mm,将相关参数代入式(14),可得到不同接触形式齿面的最大接触应力,如表1所示。由表1可知,凸凹接触形式的齿面接触应力相比于凸凸接触降低了28.95%,相比于凸平降低了19.17%。对于齿面为点接触的线齿轮而言,可以有效地提高齿面接触强度。因此,凸凹接触形式的内啮合线齿轮副最具研究价值,也是本文所研究的主要对象。

表1 不同接触形式的最大接触应力Table 1 Maximum contact stress of different contacts

3 实例分析

3.1 纯滚动内啮合线齿轮齿面构建

在坐标系S1中,小齿轮齿面接触线R1参数方程为

(15)

式中:m为圆柱螺旋线的螺旋半径;n为节距系数。圆柱螺旋线R1的螺旋升角为

φ1=arctan(n/m)

(16)

根据式(6),可得到R1在接触点的主法矢向量

(17)

根据式(5),可得到接触点的啮合方程

(18)

通过化简式(18),可以得到t与θ1的关系为

t=θ1

(19)

联合式(1)(7)(8)(19),可得齿圈接触线参数方程为

(20)

若令m2=m+E,T=t/i12,式(20)可转化为

(21)

式中:n2=i12n。

通过对比式(15)与(21)不难发现,接触线R1和接触线R2参数方程形式相同,都是圆柱接触线,并且同为右旋螺旋线,如图8所示。圆柱螺旋线R2螺旋升角为

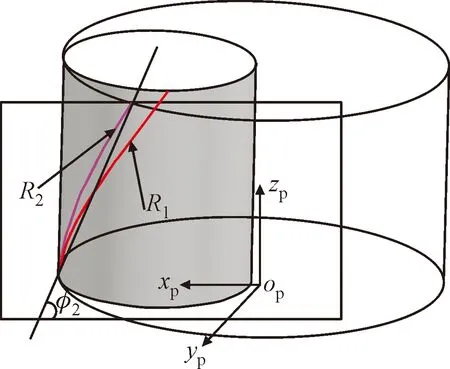
图8 圆柱螺旋线Fig.8 The cylindrical helix

φ2=arctan(n2/m2)

(22)

(23)

通过化简式(23),可得到

m=E/(i12-1)

(24)

结合式(22)和(24),接触线R2的螺旋升角可表示为

(25)

由式(24)可知,纯滚动平行轴内啮合线齿轮的中心距和传动比确定时,圆柱螺旋线的螺旋半径也随之确定。当中心距和螺旋半径满足式(24)时,主动螺旋线和从动螺旋线螺旋升角相等。

通过上述讨论,总结出选取圆柱螺旋线作为接触线的纯滚动啮合条件:

(1)接触线R1和R2螺旋升角相等且旋向相同;

(2)螺旋半径m和中心距E满足关系式(24)。

3.2 运动学仿真

根据平行轴内啮合线齿轮齿面生成方法以及纯滚动啮合条件,运用NX8.5构建精确的线齿轮副实体模型。本文建模的基本参数如表1所示,创建的线齿轮副三维实体模型如图9所示。

表2 设计线齿轮副相关参数Table 2 Relevant parameters of line gear pair design

(a)小齿轮

重合度大于或等于1是保证齿轮连续啮合传动并保证传动连续性和稳定性的必要条件。本文主动轮的齿数为6,根据文献[3]的重合度计算公式,可以得到线齿轮的重合度为

(26)

当重合度为1.5时,部分状态为2对齿参与啮合,2对齿都是基于纯滚动条件建立的齿面,所以线齿轮副连续传动过程都能保持纯滚动啮合状态。

对安装的线齿轮副进行运动学仿真,如图10所示。给定与小齿轮固联的输入轴角速度为ω1,设置小齿轮和齿圈的接触形式为3D接触,通过速度传感器测得齿圈的角速度曲线ω2,如图11所示。小齿轮角速度为10 rad/s,齿圈角速度在4.84～5.11 rad/s波动,平均传动比为2.00,均方差为5.1×10-4,最大变化值为0.07。实验结果表明:通过本文方法构建的纯滚动平行轴内啮合线齿轮机构可实现平稳、连续的速度传递,满足设计传动比需求,验证了齿面设计方法的可行性。相比于理论值,运动仿真误差的来源有:齿面变形导致了瞬时接触路径与理论接触路径的偏差[22];计算机储存数据长度有限引入误差,在求解时,误差随着迭代次数放大。

图10 运动学仿真模型Fig.10 Kinematic simulation model

图11 小齿轮和齿圈角速度曲线Fig.11 Angular velocity curves of pinion and gear ring

4 结 论

(1)基于空间曲线共轭啮合理论,研究了一种纯滚动内啮合线齿轮副的构建方法,建立了凸凸接触、凸凹接触和凸平接触的齿面数学模型。凸凹齿面曲率半径最大,相同载荷条件下齿面接触应力最小。

(2)以圆柱螺旋线为例,求解了一对共轭接触线,推导出了纯滚动啮合条件:小齿轮和齿圈接触线旋向相同、螺旋升角相等,且满足关系式E=m(i12-1)。

(3)根据齿面方程构建了线齿轮副模型,并进行运动学仿真,实验表明:通过本文方法构建的平行轴纯滚动内啮合线齿轮机构可以实现平稳、连续传动,满足设计传动比需求。