压电式力传感器的低频补偿技术及其验证

孙显达，夏吉天

（中国人民解放军63867部队，吉林 白城 137001）

1. 压电式力传感器低频补偿技术研究背景

在科学技术不断发展的今天，传感器技术已经得到了快速地普及和应用。也被成功应用到了航天、航空以及物联网等领域。在众多传感器当中，压电式力传感器也是使用范围相对广泛的类型，已经被人们所认可和接受。在压力测试系统当中，压力传感器可以对待测压力进行精准捕捉。压力传感器的特性可以分为静态和动态两种形式，在某些压力测试当中，需要对变化比较小或者不变的压力值进行测量，这里就是静态特点的呈现；也有时需要对变化形式比较剧烈的压力信号进行测量，这就是动态特点的表现。

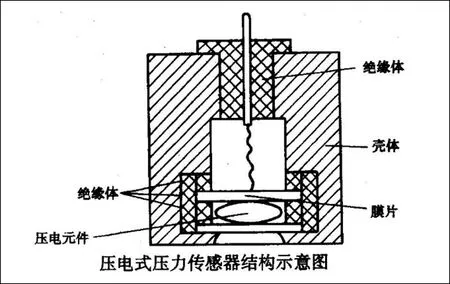
当前在国内外的已有研究结果当中，相关学者开展的研究也比较全面和深入。更多是关注到压力传感器的静态特点，一般的压力传感器技术资料也都会标注到其涉及到的属于静态指标。实际应用当中还是比较缺少动态校准设备，所以导致压力传感器当中的动态特点研究比较少，尤其是与低频动态特点相关的研究还比较少。尤其是这些年来，我国的新兴制造业加快了发展的步伐，对于动态压力测量的要求也越来越多。需要对多个瞬态过程当中压力所发生的变化规律进行深入定量的了解。这就对于压力测试系统当中的动态特点有了更高的需求。压电式力传感器本就代表着传感器技术的最前端水平，若连它都具有比较差的动态性，就无法对压力信号开展快速、准确的测试，也就无法为之后的模块测试提供更加准确的信息，也会让结果出现更为显著的动态误差。

随着越来越多的人关注到压电式力传感器的动态特点和低频补偿技术，也会有更多的人了解到传感器不同的动态指标。若传感器所具有的某些特点，无法让测试需求得到更好满足时，需要采取相应的方法来让测试提出的需求得到有效满足。这必然也会对该领域的发展产生更加深远和明显的影响，对于科学技术的发展也会产生更有力的推动作用。

2. 压电式力传感器补偿原理和方法

压电式力传感器不管外在的结构形式存在着多大的差别，内部的工作原理很多都是相似的。可以将不同外在形式的压电式力传感器工作原理进行简化，让其可以变成更加容易理解的形式。在结构当中包含了阻尼器、集中弹簧、集中质量以及二阶单自由度系统。如果传感器感受到了冲击加速度，就能够得到微分方程。

2.1 补偿原理

微振动六分量测试平台是当前国内外测试航天器活动部件微振动特点的关键平台。而压电式力传感器则是这一平台当中比较有效的传感器，主要是因为其具备了更高的分辨率和灵敏度，测量范围、频响也都更加优越。但压电式力传感器也有一定的缺点，比如具有比较差的低频响应特点，这样所得到的低频区测试数据就比较不可信。所以针对此类传感器在低频响应方面出现的问题，需要找到一定的补偿方法。

压电式力传感器低频响应，当前常见的补偿方法主要是：第一，对传感器的设计参数和结构进行改变；第二，针对传感器输出之后的信号开展进一步的处理。一般情况下，在这两种方法当中，第一种方法在具体应用的过程当中会受到比较多外部条件的制约，实现难度也比较大。所以在本次研究当中针对压电式力传感器的低频响应性差的问题，采取的是第二种补偿方法。还开展了具体的试验进行验证。

2.2 补偿方法

压电式力传感器所使用到的等效电路以及在实际应用当中所采用到的电路都有一些学者开展了相应的研究。此种传感器所受到的外部压力，采用F(t）来表示，和放大器输出电压，一起可以采用微分方程来表示：

在该公式当中，压电常数采用e表示，压电元件工作面积采用A表示，等效电阻、电容分别采用R和C表示。另外，根据这一公式，还可以得到压电式传感器所受到的外部压力和输出电压之间的相关性，也能采用公式来进行表示：

在这个公式当中，电压灵敏度采用K=eA/C来进行表示，所代表的是该传感器放电的时间常数。一般情况下，传感器所接受的外部压F，可以采用传感器的输出电压除以电压灵敏度得出结果。因为公式当中的k属于常数，所以需要将公式两端都开展傅里叶变换。

3. 压电式力传感器低频补偿技术应用实验验证方法

在本次所开展的关于压电式力传感器低频补偿技术应用的相关验证实验当中，所采用的方法是p5H压电陶瓷片方式。整个实验过程主要划分为两个部分：第一，需要先辨识清楚p5H压电陶瓷片对于电压的灵敏度情况，还有放电的时间常数值。这样可以得到补偿函数；第二，针对p5H压电陶瓷片，要确定其在已知的简谐外力以及阶跃外力情况下得到的测试结果，完成进一步的补偿。还要对比分析已经测得的外力结果和实验得到的补偿结果。对本次研究提出的补偿方法开展进一步的验证分析。

3.1 设定参数，完成辨识

在阶跃外力的作用情况下，所得到的压电式力传感器电压响应计算公式如下：

在本公式当中，阶跃外力的变化幅值用a表示，电压灵敏度以及放电时间常数分别采用k和来表示。还可以基于该公式，得到在阶跃外力整体环境的影响下，压电式力传感器的整体响应曲线。本次研究所测试的是在阶跃外力环境影响下，压电陶瓷片的响应变化结果。然后再采用曲线拟合的方式处理得到的结果，完成进一步的参数辨识。

在具体开展的实验当中，需要使用到特制的夹具，压紧并且在大质量刚性试验台上，将电陶瓷片固定好。夹具包含了受力和固定部分。在受力部分上需要固定专门的电磁铁。如果电磁铁成功通电后，就可以直接吸附标准砝码。等到电陶瓷片的放电逐渐减少到零，然后电磁铁忽然断电之后。由于受到重力的影响，砝码会直接和电磁铁脱离，这样就能够让压电陶瓷片接收到正阶跃外力。

为了让辨识参数的精准度不断提高，在本次研究当中，电陶瓷片所施加的砝码分别是1kg、2kg、3kg的砝码，还对这些砝码施加之后电陶瓷片的电压时域响应情况开展了分别测试。还对得出的结果，采用MATLB曲线拟合工具完成相应的拟合。得到的拟合优度结果为：

U1（t）和方差为0.01，确定系数为0.96，均方根为0.02；U2（t）的和方差为0.01，确定系数为0.99，均方根为0.01；U3（t）的和方差为0.03，确定系数为0.98，均方根为0.03.按照这些数据，还能够得到压电陶瓷片放电时间和电压灵敏度之间的关系结果。其中放电时间计算出的结果为0.09s，电压灵敏度得出的计算结果为0.018V/N。在计算得到这些数值之后，也能够得到本次研究的电陶瓷片补偿函数，如下：

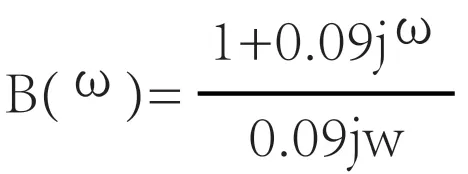
3.2 补偿方法的验证

在本研究当中提出针对压电式力传感器的低频问题，采用第二种补偿方式，即需要对传感器输出之后的信号开展相应的处理。为了验证提出这一补偿方法的可行性，也设计了实验进行专门的验证。所纳入的也是p5H压电陶瓷片。在简谐外力和阶跃外力条件都已知的情况下开展进一步的补偿。所选择的砝码质量为1.5kg，确定的阶跃外力变化幅度值是14.7N。按照计算结果所得，在补偿之前测试得出的结果为0.63F/N，补偿之后得到的结果为14.8F/N。

就简谐外力加载的具体方式主要是：需要在夹具受力的上方，悬挂一根质地相对比较柔软的弹簧。将质量块悬挂在弹簧的另外一端。在某初始条件下，当质量块处于上下不断运动的过程中时，压电陶瓷片就会受到简谐外力。而且所受到的此种简谐外力和质量块之间存在着密切的相关性，这两者呈现出正向变化关系，即随着质量块的变动，简谐外力正向变动。为了对质量块在不断振动当中产生的加速度开展相应的计算，需要将加速度传感器粘贴到质量块上。本次研究当中也使用到了加速度传感器，具体的类型为电容式传感器，之所以选择该类型，主要是因为其测试范围更加广泛一些，能够达到0Hz。实验实际开展的过程中，还需要采用LMS数据采集和测试系统来测量电陶瓷片输出电压的时域响应数据和软弹簧简谐振动过程当中质量块的不同加速度结果。

在分别得到加速度传感器的输出电压和时域测试结果之后，还要开展傅里叶变换。这样能够得出与简谐外力频域相关的计算结果。与此同时，将电压陶瓷片输出电压完成计算和傅里叶变换之后，也能得到在补偿之前压电陶瓷片的频域测试结果。

3.3 结果分析

根据上述一系列的计算过程，得到了相应的计算结果。研究发现：压电式电传感器在高频的响应方面整体上比较好，但是对于低频领域的响应效果却比较差。因此需要针对低频响应问题采取补偿措施。在分析了常见的低频补偿措施之后，发现对传感器的输出结果进行处理是更好的补偿方法。因此，研究当中就设计实验来验证这一补偿方法是否可行。实验当中让压电式力传感器处于阶跃外力作用下，补偿其低频响应特性。根据得出的结果发现，当压电式力传感器受到阶跃外力的作用，可以有效补偿低频响应问题。简谐外力的振动幅值和频率分别为3.82N和1.23Hz，这属于明显的低频区。另外，也能根据计算得出的结果发现在补偿之前的测试结果为2.33N。这一结果与处于简谐外力所得出的振动赋值存在着比较大的差别。在补偿，得出的结果为3.81N，而这一结果就和处于简谐外力作用下的振动幅值结果有比较强的一致性。

通过开展系列的计算过程，还能够发现当压电陶瓷片处于简谐外力作用下，补偿之前和补偿之后，在1.3HZ时，所得到的振动相位结果是：0.6，0.8,0.5.也就说明，补偿之前的和简谐外力作用下的振动相位存在着明显的差异；而在补偿之后和简谐外力下的振动相位结果就比较接近。说明采取的低频补偿措施的确起到了一定的作用。

4. 结语

尽管压电式力传感器当前的使用范围已经变得越来越广泛，也被成功应用在不少领域当中。但是我们发现过去的很多研究当中关注的都是传感器的高频应用特性，很少会关注到低频应用特性。由于压电式力传感器本身的特殊性，其低频响应存在着比较大的问题，导致在低频情况下得出的结果准确性差。基于这一背景，本次研究通过理论结合实验验证相结合的方法提出和验证了一种关于压电式力传感器低频补偿方法。研究当中发现对传感器输出的数据开展进一步的处理是一种较好的补充低频响应问题的方法，减少其存在弊端对于适用范围的限制。