机场的出租车问题研究

陈黎茜

（重庆邮电大学，重庆400065）

大多数乘客下飞机后要去市区的目的地，机场与城市之间的交通方式主要有[1]：轨道交通、直达巴士、常规公共交通、私人汽车以及出租车。国内大多数是机场将送客和载客通道分开的，送客到机场的出租车将面临两种方案选择：从出发区前往到达区排队等待载客返回市区；直接放空返回市区拉客。

根据中国民航飞机型号介绍国内机场常见的飞机机型[2]，波音747载客数在350-400人左右。机场出租车管理人员负责“分批定量”放行“蓄车池”内排队的出租车进入乘客停留的“乘车区”，同时安排一定数量的乘客上车。某段时间抵达机场的航班数量和“蓄车池”内排队的出租车数量是司机可观测的确定信息，通常司机根据个人经验做出判断，本文旨在通过数学分析给出司机的决策方案。

1. 模型I的建立与求解

设“蓄车池”内已有n辆出租车，机场到市区的距离为S米,出租车在第i时间内的起步价为元/千米、里程费为元/千米，出租车单位油耗费用为µ元/千米，机场高速限速米/秒，市区公路限速米/秒。

为综合考虑出租车潜在载客收益，将在第i时间内第n+1个司机选择A、B两种方案的收益差值作为模型的决策准则，则决策准则为：

根据出租车计价方式和油耗损失计算得：

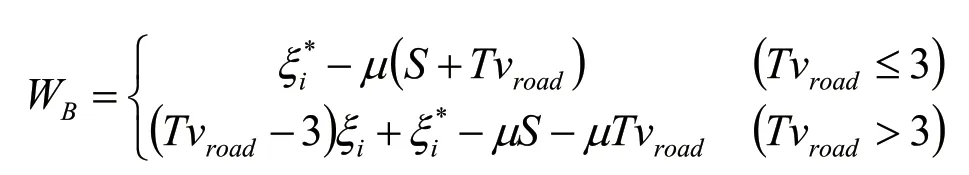
第n+1个出租车司机选择A方案时，在“蓄车池”内的出租车的等待时间与到达机场且可能乘坐出租车的乘客人数和前一小时机场出发且可能乘坐出租车的乘客人数有关，关系表达式为：

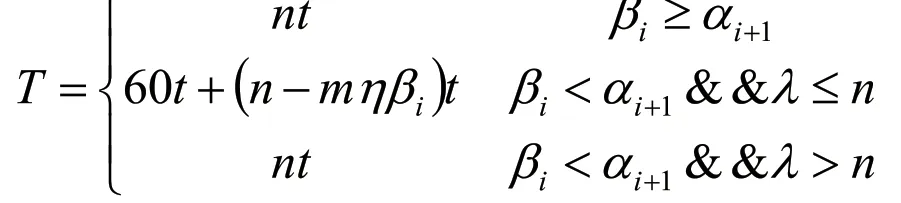
（其中m为每列航班的载客量，η为乘坐出租车出行的乘客的比率）

使用根据胡春华[3]的研究，天河机场现状交通方式结构为机场大巴占比23.53%，出租车占比28.21%，小汽车33.84%，其他方式14.42%。

（武汉天河机场[4]是为中国中部首家4F级民用国际机场、对外开放的一类航空口岸，故本文用武汉天河机场现状交通方式结构表示我国现状交通方式结构，本文中的值为η）。

由“蓄车池”出租车数量，机场到市区的距离,起步价，里程费以及限速值可建立计算方案收益差的模型Ⅰ。

通过建立模型I给出在第i时间内第n+1个出租车司机的决策策略为当：，选择方案A；当选择方案B。

2. 模型II的建立与求解

指数平滑法是布朗(Robert G..Brown)所提出，其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均[5]。

通过回归分析得到线性回归方程如下：

由此可知：决策准则对排队出租车数量的依赖性大于对航班差值的依赖性，且排队出租车的数量越大、航班差值越小司机越可能选择B方案。

由此本文给出上海浦东机场出租车司机选择方案为，当时间为23：00—5：00时，当n＞78时选择B方案，当n≤78时选择A方案，时间为5：00—23：00时，当n＞82时选择方案B，当n≤82时，选择方案A。

3. 模型III的建立与求解

高峰期的服从参数为：

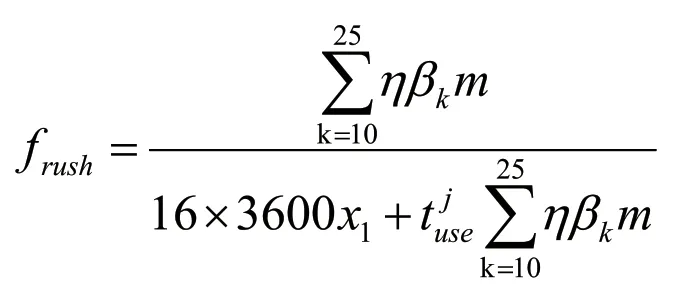
低峰期的服从参数为：

系统内乘客的服务时间服从负指数分布，其服从参数λ为单位时间平均服务的乘客凭此数即为，设：“乘车区”的停车位长为l，乘客步行速度为，乘客由“乘车区”入口进入到达上车点所用时间为，每批乘客的平均逗留时间为则客由“乘车区”入口进入到达上车点所用时间服从分以下两种情形。

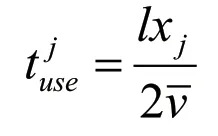
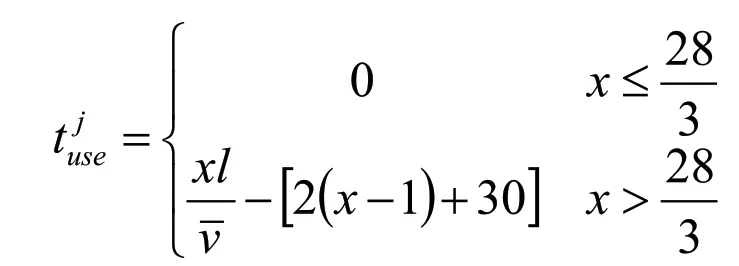
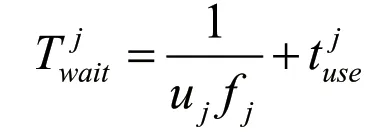
以上海浦东机场为例，经过MATLAB软件仿真得知，两种出租车排队服务系统的设置方案为对于多点并列式出租车排队服务系统，在高峰期设置上车点数量为28个，人均逗留时间为8.26；低峰期上车点数量设置为16，人均逗留时间7.72；对于多点单列式出租车排队服务系统，高峰期上车点数量设置为60，人均逗留时间8.81；低峰期上车点数量设置为28，人均逗留时间为6.95。

通过比较乘客的平均逗留时间得到为了提高总的乘车效率，管理部门应该在高峰期（9：00—1：00）开放并行车道设置并行28个上车点；在低峰期（1：00—9：00）开放单行车道设置并行28个上车点。

4. 结语

针对模型Ⅰ，本文考虑机场乘客数量的变化规律和出租车司机的收益，得到以车辆数、里程费、油耗等为影响因子，以收益差值作为决策准则建立出租车司机选择决策模型。

针对模型Ⅱ，本文通过winters可加性指数平滑法建立时间序列模型，得到浦东机场的吞吐量与时间的关系，给出浦东机场出租车司机的选择方案。通过处理数据进行模型统计量分析和回归分析，发现决策准则对排队出租车数量的依赖性大于对航班差值的依赖性，司机可根据时间以及车数选择去留方案。

针对模型Ⅲ，本文通过建立M/M/1型排队论模型讨论多点并（单）行出租车排队服务系统在高（低）峰期的上车点数量和每批乘客在“乘车区”的逗留时间，比较人均逗留时间的大小得到最优的上车点设置方案。

5. 模型改进

考虑排队论模型较为理想化，其结果不能做到深度分析，故采用元胞自动机模型对原有模型进行定量补充扩展。元胞自动机能够有效模拟交通流中车辆的微观运动,便于研究车辆间的相互作用机理[7]。

在M/M/1型排队论的基础上,定量分析出租车转向以及客流干扰造成的时间冲突，对交通现象进模拟，在交通系统中，车辆运动模拟采用Nasch模型[8]。

综合考虑左转车辆抢行,通过基于两股车流到达冲突点的时间差变化的Logisitic型抢行概率以及多左转路径选择,在此基础上加入行人干扰因素，建立了更加符合实际交通状况的两相位交叉口直行－左转机动车－行人冲突模型[9]。