复杂曲面屋盖脉动风压的非高斯特性及峰值因子研究

杨雄伟， 周 强,2， 李明水,2， 王沛源

(1. 西南交通大学 风工程试验研究中心，成都 610031; 2. 风工程四川省重点实验室，成都 611756)

随着设计建造技术的进步和人们对空间使用需要的提高，屋盖结构向大跨度、轻质量、复杂造型等方向快速发展，导致结构刚度变小、阻尼变低，对自然风的作用更加敏感。风荷载已成为大跨曲面屋盖结构设计的主要控制荷载，强风导致大跨曲面屋盖特别是其围护结构的破坏时有发生[1-2]。因此，针对大跨曲面屋盖风荷载及其风致振动的研究一直都是结构风工程界的研究热点之一。

在传统的结构抗风设计方法或规范中，通常认为屋盖表面脉动风压符合高斯分布，然后采用统一的峰值因子计算其极值风压[3-7]。然而，随着对大跨屋盖风荷载特性研究的逐步深入，国内外学者发现在屋盖迎风前缘及拐角附近等存在流动分离的区域，脉动风荷载呈现较显著的非高斯特性[8-10]。若仍采用高斯分布描述该区域的脉动风荷载，并按照规范给出的峰值因子进行结构特别是围护结构的抗风设计，将低估其极值风压，给结构设计带来安全隐患。Kumar等[11-12]认为任何屋盖结构的风荷载分布都存在高斯区和非高斯区，指出了非高斯区常常位于气流分离区域，并对低矮平屋盖和人字形屋盖的高斯和非高斯区域进行了划分。叶继红等[13]在研究大跨度柱壳屋盖结构的脉动风荷载时，发现非高斯区域往往集中在来流前缘，后部尾流区及高点角区附近，并指出应适当提高规范中的峰值因子以确保结构抗风安全。

为此，学者们建立和发展了脉动风压的非高斯分布模型，以获得较为精确的极值风压。Kareem等[14-15]将非高斯分布表示成高斯分布的Hermite级数形式，并建立了基于高阶统计量的峰值因子模型。Winterstein等[16]提出了将非高斯过程转换为高斯过程的方法，建立基于矩的随机振动Hermite模型。在此基础上，Ding等[17]针对硬非高斯过程建立了基于Hermite矩的转换模型。Yang等[18]采用多样本风压系数时程的偏度、峰度表示Hermite矩模型，并根据其形状参数和高斯分布峰值因子建立了非高斯峰值因子的概率密度模型。此外，还有学者基于极值理论进行结构风压极值分析[19-20]。

综上可见，针对屋盖脉动风压的非高斯特性研究多关注平屋盖、柱面或马鞍形屋盖，对复杂曲面屋盖脉动风压鲜有研究，然而此类曲面结构的风场绕流更加复杂，表面脉动风压分布特性也因此存在较大差异。其次针对脉动风压非高斯特性与峰值因子联系的研究，以及关于非高斯特性形成机理的研究也较少开展。此外，针对高斯与非高斯区域的划分标准多基于简单的偏度和峰度范围，缺乏明确的物理机理。

为此，本文以某大跨复杂曲面屋盖为研究对象，通过刚体模型风洞测压试验，研究表面脉动风压的概率分布规律，分析脉动风荷载的非高斯特性及其形成机理，首次提出以空间相关性作为划分高斯分布和非高斯分布的标准，然后基于Hermite矩模型构建非高斯分布与峰值因子间的联系，并给出此类屋面非高斯区域风荷载峰值因子的取值范围。

1 风洞试验概况

1.1 试验模型设计及工况设置

风洞试验对象为结构新颖、造型独特的大跨曲面屋盖。此屋盖长304 m，宽96 m，高约24 m，如图1所示。按照几何缩尺比为1∶100进行刚性模型设计，对应的试验阻塞比小于5%。模型采用有机玻璃与ABS塑料制成，以满足模型刚度和外形要求。

图1 屋盖效果图Fig.1 Roof renderings

为准确获取表面风荷载，在屋盖表面共布置406个测压点，同时鉴于屋盖边缘和曲面顶部流动分离显著及风荷载特性复杂，因此对上述区域进行了测点加密处理，如图2所示。在试验工况设置方面，在0°～360°风向角范围内每隔10°(如图2所示)进行测试并采集数据。压力测量与数据采集系统为Scanvalve电子扫描阀，采样频率为256 Hz，采样时长为60 s，满足试验相似比要求。

图2 屋盖测点布置和风向角设置Fig.2 Distributions of pressure taps on the roof and wind direction

1.2 紊流风场模拟

测压试验在西南交通大学XNJD-3风洞中进行。该风洞试验段尺寸为22.5 m(宽)×4.5 m(高)×36 m(长)，是目前世界最大的大气边界层风洞，风速范围为1.0～16.5 m/s。试验采用尖塔和粗糙元等被动措施模拟GB 50009—2012《建筑结构荷载规范》[21]规定的B类紊流风场。图3(a)给出了风洞模拟得到的平均风速和湍流强度剖面，其中，ZG，UG和IU分别为梯度风高度、梯度风速和湍流强度。由图3(a)可见，试验值与《建筑结构荷载规范》的规范值基本一致。图3(b)给出了试验实测的顺风向脉动风速谱，其中,k1为折减频率，可见试验值与Von Karman谱吻合较好。

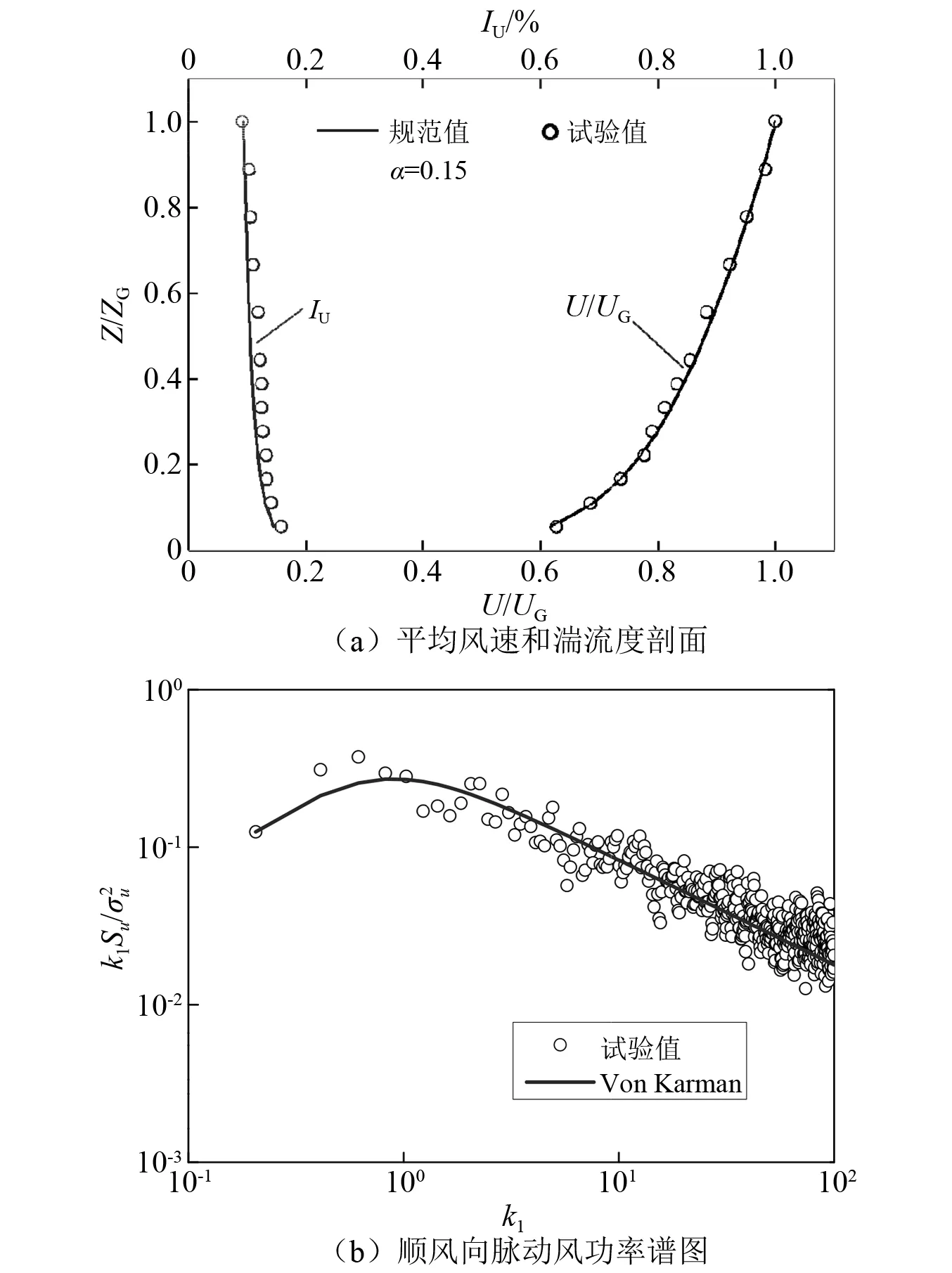
图3 风洞模拟的B类大气边界层Fig.3 Wind tunnel simulation for terrain B

2 结果与讨论

限于篇幅，本文只选取部分风向角下的风压分布结果作为典型情况做介绍。

2.1 脉动风荷载概率分布特性

高斯分布可以由前两阶统计量(均值及方差)完全表示。对于非高斯分布，则采用三阶统计量(偏度，γ3)和四阶统计量(峰度，γ4)来表述风压信号概率分布的偏离和凸起程度，即表示非高斯分布概率性质的重要指标。式(1)、式(2)分别给出了某一测点脉动风压的偏度和峰度计算公式

(1)

(2)

式中:γ3和γ4分别为该测点脉动风压的偏度和峰度；Cpi为该测点的风压系数；μ为该测点的平均风压系数；σ为该测点风压系数的均方根值；N为该测点风压的试验采样数量。

通过对测点脉动风压的偏度和峰度的分析，可定量判断其偏离高斯分布的程度。鉴于屋盖是对称结构，图4给出了0°，40°，90°和180°风向角下屋盖表面各测点脉动风压的偏度和峰度散点图，其中横坐标为测点风压的偏度值，纵坐标为相应的峰度值，并采用最小二乘法对0°风向角下的偏度与峰度关系进行了拟合。

图4 不同风向角下偏度-峰度散点图Fig.4 Scatter diagram of skewness and kurtosis with different wind directions

由图4可以发现，测点脉动风压的偏度与峰度间的分布较为离散，且不同风向角下存在一定的偏差，但两者大致呈现非线性关系，这与Gioffre等获得的高层建筑风压分布，以及孙瑛等获得的大跨平屋盖风压分布基本相似。大部分测点风压的偏度和峰度都在-0.6<γ3<0及3.0<γ4<4.0范围内，而其他测点风压的偏度和峰度相较于标准高斯分布出现了严重的偏离。还可以发现，不同风向角下测点风压的偏度大多为负值，长尾在负向，即在吸力一侧。由于屋盖大部分区域的平均风压为负压区(吸力作用)，因此屋盖脉动风压的负偏度使得其极值风压更加显著。

为进一步分析屋盖表面脉动风压的非高斯分布特性，图5给出了0°和180°风向角下屋盖上典型测点(测点位置及编号见图2)脉动风压概率密度函数，并与标准高斯分布曲线进行比较。图中横坐标为经标准化处理后的风压系数，即(Cp-μ)/σ，纵坐标为概率密度(probability density function，PDF)。由图5(a)～图5(c)可见，位于屋盖边缘A条带上测点的脉动风压概率分布函数均明显偏离高斯分布曲线，不满足高斯分布。通过与标准高斯分布曲线上相应值的比较可以发现，0°风向角下测点A7和A12的最大误差分别达到29.5%和21.0%，即呈现出强烈的非高斯分布特性。由图5(d)～图5(f)可见，当条带B上的测点B1和B14分别处于迎风侧时(即分别对应180°和0°风向角的迎风侧前缘)，其脉动风压的概率密度分布也明显与标准高斯分布存在偏离，呈现出显著风非高斯分布。位于屋盖中部测点B7脉动风压的概率分布与标准高斯分布比较吻合。与此类似，条带C上边缘测点的脉动风压概率分布与条带B存在相似的规律，但180°风向角下，中间测点C12的脉动风压具有较强的非高斯特性，其原因是曲面屋盖导致测点C12处于分离泡内。在其他风向角下，脉动风压概率密度存在类似的分布规律，限于篇幅不作详细介绍。

图5 0°和180°风向角下典型测点风压概率密度分布曲线Fig.5 Probability density function of fluctuating pressure of typical taps with wind directions of 0° and 180°

此外，与平屋盖和柱面屋盖不同，曲面屋盖在0°风向角下迎风侧前缘测点(如测点B14和C24)的非高斯特性不如180°风向角下迎风侧前缘测点(如测点B1和C1)，如图6所示。其原因在于：0°风向角下，屋盖迎风前缘为曲线，影响分离泡的形成，破坏了旋涡的展向相关性。

综合以上分析可见，曲面屋盖脉动风压呈现较强的非高斯特性，特别是迎风侧前缘和屋盖边缘区域的测点显著受到流动分离而形成大尺度旋涡的影响，其脉动风压的概率密度分布、偏度和峰度与高斯分布存在明显偏离和凸起，且长尾在负值一侧。

图6 不同风向角下迎风前缘测点脉动风压概率密度分布比较Fig.6 Comparison for the probability density function of fluctuating pressure on the leading edge with different wind directions

2.2 非高斯分布与流场结构的关系

屋盖绕流流场结构直接决定了其表面脉动风压的分布特性[22]，如当大尺度旋涡作用于屋盖结构表面时，处于旋涡区内测点的脉动风压具有较强的相关性，不满足独立同分布条件，呈现非高斯特性；当测点位于大尺度旋涡破裂形成的多个小尺度旋涡区域时，其脉动风压的相关性较弱，满足独立同分布条件，即基本符合高斯分布。为此，本文通过计算任意两测点间空间相关性，分析屋盖绕流的空间结构及旋涡发展形态，进而揭示屋面脉动风压非高斯分布特性的流场演化机理。式(3)给出了相关系数的表达式

(3)

式中:σCpi和σCpj分别为i和j测点风压系数时程的标准差；cov(Cpi,Cpj)为i和j测点风压系数时程的协方差。一般认为当ρ>0.5时，视为强相关；而当ρ<0.2时，则属于弱相关。

已有研究表明，脉动风荷载非高斯区域常出现于气流分流后的大尺度旋涡内，而旋涡结构与风压的空间相关性存在密切的逻辑联系。因此，这里主要研究各测点与第1个测点(即最靠近流动分离点)的相关性，并据此推测旋涡结构及风荷载的非高斯特性。图7给出了0°与180°风向角下分别沿条带A、条带B和条带C的测点脉动风压空间相关系数，图中：Li,j为两测点间的距离；H为条带长度。由图7可见，在0°风向角下靠近迎风侧边缘的测点脉动风压空间相关性较强，其原因是：气流经过迎风侧边缘时产生分离，从而形成大尺度旋涡，使得旋涡内的测点风压具有强空间相关性，且非高斯特性突显；而后随着测点远离屋盖迎风前缘，气流发生再附，大尺度旋涡逐渐衰减脱落为的较小尺度旋涡，其脉动风压的空间相关性迅速衰减，逐渐满足独立同分布条件。在180°风向角下测点的空间相关性与0°风向角存在相似的规律，但由于180°风向角下迎风侧前缘为近似直线型，故分离涡的展向同步性更好，更易形成尺度更大的分离涡，故其测点脉动风压的空间相关性较0°风向角更强。

2.3 风压非高斯分布区域划分

图8和图9分别给出了0°和180°风向角下屋盖表面风压信号的偏度和峰度等值线图。由图8可以得出，0°风向角下，位于屋盖的迎风前缘位置，因气流分离致使风压信号呈现负偏和上凸分布；而位于屋盖迎风侧后方的绝大部分区域，偏度值在0附近，峰度值在3左右，属于高斯区域。图9在180°风向角下测点的偏度和峰度的分布与0°风向角存在类似规律，但由于180°风向角下迎风侧前缘为近似直线型，故柱状涡的展向同步性更好，其影响范围也更广，故其风压信号的非高斯特性较0°风向角更明显。这与上小节空间相关性研究所得结论一致。

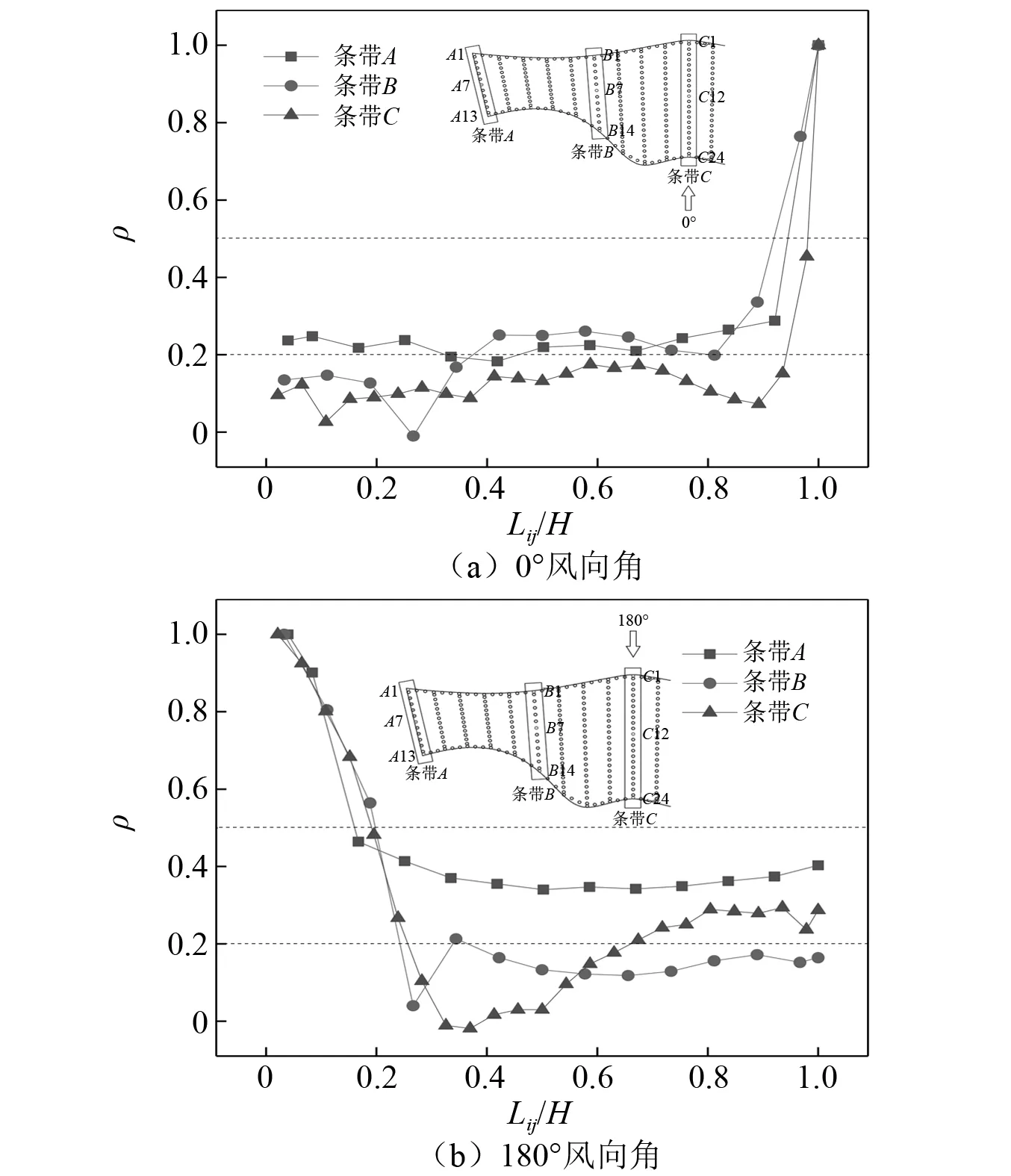
图7 屋盖表面典型测点的空间相关性Fig.7 Spatial correlation of pressure taps on roof

图8 0°风向角下脉动风压的偏度和峰度云图Fig.8 Contours of skewness and kurtosis on wind angle of 0°

图9 180°风向角下脉动风压的偏度和峰度云图Fig.9 Contours of skewness and kurtosis on wind angle of 180°

由于大跨屋盖形式复杂多样，因此目前针对大跨屋盖脉动风压的高斯分布与非高斯分布的划分标准还没有形成较为统一认识。Gioffre等[23]认为以偏度绝对值|γ3|>0.5且峰度值作为标准γ4>3.5，划分柱形高层建筑的非高斯分布是比较合理的。孙瑛等认为平屋盖表面风压分布若满足|γ3|>0.2且γ4>3.7，则可近似认为其满足非高斯分布。柯世堂等[24]建议冷却塔表面脉动风压的非高斯分布需满足以下条件之一：①γ3>0.2且γ4>3.2；②γ3>0.45；③γ4>4.0。李玉学等在对划分柱面屋盖的非高斯分布时，综合考虑偏度和峰度的影响，选取偏度和峰度的累积概率均达到80%作为划分标准。目前针对复杂曲面屋盖尚无相关划分标准研究。

基于简单的偏度和峰度范围进行判别难以具有较好的说服性。鉴于此，本文分别从风压时程特性和流动特性角度，采用风压分布的空间相关性、偏度和峰度的累积分布函数(cumulative distribution function,CDF)曲线两种标准，对屋盖风压进行高斯与非高斯分布的划分。

图10给出了0°和180°两个代表性风向角下表面脉动风压的偏度和峰度的累积分布函数。这里选取偏度和峰度的累积分布均达到90%为区别高斯分布与非高斯分布临界点。需要说明的是，测点风压的偏度值正负，表明其概率分布右偏或者左偏，均不符合高斯分布，因此，对于非高斯区的判断标准，偏度值应取绝对值。由图10可见，在不同风向角下临界点的出现位置差异明显，由此说明需要对全风向角下结构表面脉动风荷载非高斯分布区域范围进行分别划分。图10(a)表明在0°风向角下，当测点风压的偏度值和峰度值分别满足|γ3|>0.02和γ4>4.39时，则该测点表征的区域属于非高斯区。由图10(b)可知，在180°风向角下，当测点风压的偏度值和峰度值分别满足|γ3|>0.11和γ4>4.94时，此区域属于非高斯区。对于风压分布空间相关性的划分标准，将相关系数大于0.5(强相关)作为划分非高斯区的依据，即屋盖边缘测点风压的空间相关性较强则表明受同一大尺度分离涡影响，其非高斯特性显著。这里分别将前后两种标准分别定为标准I和标准II。

图11为依据标准I得到的划分结果，并给出了偏度和峰度的累积分布均达到80%的情况。图12为依据标准Ⅱ(相关系数>0.5)得到的划分结果，图中阴影部分表示非高斯区，其他为高斯区。对比两图可以发现，偏度和峰度的累积分布均达到80%划分的非高斯区域以及相关系数大于0.5划分的非高斯区域基本一致，且要比偏度和峰度的累积分布均达到90%划分的非高斯区域要大。考虑到标准I选取的偏度和峰度所达到的累积分布具有偶然性，并将图11、图12的结果与图8、图9进行比较分析，可以发现依据标准II(相关性大于>0.5)划分的非高斯区域更加合理，且标准II与流动分离及绕流结构关系密切，具有较明确的物理意义。此外，两图阴影部分的分布规律再次说明屋盖表面非高斯区域主要位于迎风前缘气流分离区域。

图10 不同风向角下偏度和峰度的累积分布Fig.10 Cumulative distribution function of skewness and kurtosis under different wind directions

图11 非高斯区域划分(标准 I)Fig.11 Division of non-Gaussian regions (standard I)

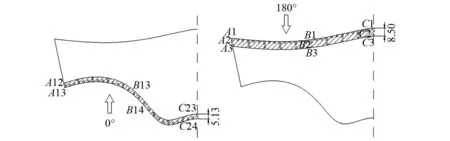
图12 图12非高斯区域划分(标准Ⅱ)Fig.12 Division of non-Gaussian regions(standard Ⅱ)

2.4 脉动风荷载非高斯峰值因子

峰值因子是确定屋盖极值风压的重要参数。本文基于风压时程的三阶矩和四阶矩，把非高斯过程转换成高斯过程的Hermite级数，其对应的峰值因子表达式为

(4)

(5)

(6)

(7)

式中，γ3,γ4分别为风压信号的三阶矩和四阶矩。

限于篇幅，这里选取非高斯区域的典型测点为对象，采用上述Hermite级数法计算其风压的非高斯峰值因子，如表1所示。表中同时给出了各测点风压的偏度值和峰度值。由表1可以看出，非高斯区的脉动风压峰值因子与风向角及测点位置密切相关，但绝大部分测点的脉动风压峰值因子都超过5，远高于《建筑结构荷载规范》的建议值。可见，若采用统一的高斯区峰值因子进行围护结构抗风设计，其结果将偏于不安全。因此，在曲面屋盖围护结构抗风设计时，其边缘和曲面拐角附近的脉动风荷载峰值因子应按照Hermite 矩模型理论确定。

表1 屋盖表面风压非高斯峰值因子

3 结 论

(1)复杂曲面屋盖表面部分区域的脉动风压呈现较强的非高斯特性，其脉动风压的概率密度分布、偏度和峰度与高斯分布存在明显偏离和凸起，且长尾在负向一侧。

(2)受流动分离而形成大尺度旋涡的影响，屋盖迎风侧边缘脉动风压的空间相关性较强，而远离屋盖边缘和曲面拐角的区域脉动风压相关性较弱，基本满足高斯分布。

(3)与基于偏度和峰度的累积分布函数的划分标准相比，基于脉动风压空间相关性的高斯区与非高斯区划分标准更加合理，其物理意义也更为明确。

(4)非高斯分布区域的脉动风压峰值因子基本大于5，远超规范建议值，因此若采用统一的高斯区峰值因子进行抗风设计有可能导致结构不安全。建议非高斯分布区域的脉动风荷载峰值因子应按照Hermite 矩模型理论确定。