基于自适应紧框架学习的轴承故障诊断

柏壮壮， 卢一相， 高清维， 孙 冬

(安徽大学 电气工程与自动化学院，合肥 230601)

滚动轴承在工业生产设备中占据重要的地位，它广泛应用于矿山、冶金和医疗等多个领域，它的运行状态将会直接影响整个系统的工作效率。与其他类型的机械部件相比，滚动轴承在摩擦损耗、装配和工作效率方面有很大的优势，因此它被广泛的用于旋转机械中。但是，如果轴承发生故障，将会引起连锁反应,如影响生产、造成财产损失、甚至危害生命。因此，对轴承运行状态的提前准确地监测和诊断，将会对生产系统的可靠安全运行有极大的帮助。

目前轴承故障检测常用的方法是振动检测法[1-2]，它可以很方便的获得轴承的运行数据。轴承的振动信号携带重要的特征，是可测量可区分的。但同时振动信号呈现的非线性和非平稳性且在噪声干扰情况下难以进行信号特征提取并诊断[3-4]。基于特征提取的故障诊断方法由三步实现：①信号预处理，如去噪；②提取振动信号的特征，这部分将振动信号转换为包含故障信息的多维特征向量；③利用分类器如神经网络[5-6]，随机森林[7]，支持向量机(support vector machine,SVM)[8]等算法实现对故障信号的自动诊断。

早期的轴承故障诊断使用时域统计信息如信号峰值、方差等，计算方便快速，在轴承故障信号特征提取方面应用较多，但故障程度的加深会导致时域特征变化较弱，从而不能较好地诊断故障，因此很多学者摒弃传统的时域特征，采用频域、时频域特征。文献[9]首先使用谱峭度分析振动信号的瞬态冲击分量所在的频带位置，然后利用双谱分析抑制噪声并突出特征频率，从而诊断轴承故障。Yang等利用经验模态(empirical mode decomposition, EMD)能量谱的方式检测故障，经验模态将复杂信号分解为有限个本征模函数(intrinsic mode function，IMF)，各IMF分量包含了原始信号不同时间尺度的局部特征信号。尽管EMD对于非平稳信号和非线性信号有时能很好的工作，但是它缺乏严格的数学证明，因此在实际应用中需要很强的经验指导[10]。文献[11]提出变分模态分解(variational mode decomposition，VMD)方法和SVM结合进行故障诊断，VMD通过迭代搜索变分模型最优解获取模态分量的频率中心和带宽，从而提取信号信息。Gilles[12]提出一种新的分解方式——经验小波变换(empirical wavelet transform，EWT)，它通过设计小波滤波器组提取信号的幅频调制分量，但它难以准确的分割非平稳信号和噪声信号的频率。为了克服EWT的缺点，Hu等[13]提出使用增强经验小波变换的方法分割非平稳信号和噪声。

小波分析法具有严格的数学推导和证明，已经成为信号分析和特征提取方法中的典型算法。Konar等采用连续小波变换提取特征，进一步采用支持向量机对故障种类进行分类，但这种方式很容易带来维数过高的风险，因为经过连续小波变换后得到的系数由许多复杂的二维信号构成。文献[14]首先使用Morlet小波进行信号小波分解，再将小波系数划分为多个子列，计算各子列协方差矩阵的特征值作为所需的故障模态的特征参数，然后使用连续隐马尔可夫模型在三种故障程度下分别实现轴承正常状态、滚珠故障、外圈故障和内圈故障的正确识别。同时为了有效提取信号的振动特性及周期性成分，该算法还使用最小香农熵准则和奇异值分解选择Morlet小波参数，实现参数优化。除了连续小波变换，小波包变换也被用来分析提取振动信号特征[15-17]。这些算法主要采用小波包能量来检测轴承故障[18-19]，如文献[20]采用小波包对振动信号进行三层分解，将振动信号分解为多个频带不同的信号，并提取各频带的相对能量特征，构建特征向量；再利用多核学习算法从训练样本中集中学习核函数与分类器；最后使用分类器进行故障分类。

小波变换之所以能够成功的应用于轴承的故障诊断，这得益于它能够完整的描述信号的特征子空间。然而，振动信号的形态多样化使得一个小波基在描述某种故障特征子空间时性能较好，对其他的故障特征子空间的描述效果却很差。因此，结构固定的小波基在描述故障特征时其性能就具有很大的不确定性，特别是当故障信号中包含多种故障时。为了解决对故障信号的自适应描述问题，有学者提出使用稀疏表达来对信号进行自适应描述，并将其应用于机械故障检测[21]。与传统的小波变换相比较，虽然这种基于数据训练出来的过完备字典在描述故障信号的特征时具有很大的灵活性，但是当参与训练的样本具有相似性的时候，会使得过完备字典原子具有明显的相关特性，将直接影响故障信号的重建效果。因此，构造一种既能够对故障信号特征进行有效自适应描述，又能够完全重建故障特征信号的紧框架是一种必然的选择。

模式识别算法是故障诊断的核心，它随着模式识别方法的发展而不断得到完善。传统的基于统计的模式识别方法和神经网络[22-23]已经被广泛地应用于故障识别领域，它通过对大量样本的学习建立故障特征到故障空间的映射关系，实现故障的诊断。虽然神经网络在实际的故障诊断中能够取得良好的效果，但是它需要大量的训练样本，在实际工程应用中，很难获得足够多的样本，尤其是故障样本，这使得在很多情况下神经网络的诊断效果都不理想。

支持向量机是由Vapnik等[24]在统计学习理论基础上发展的一种新的模式识别方法，它针对小样本条件下的机器学习问题建立的新型学习机制。它通过最小化经验风险的同时，最小化置信区间的上界，有效地解决了小样本及非线性问题。因此，它在小样本学习中拥有比神经网络更好的泛化能力，同时算法的收敛速度也很快。基于核函数的支持向量机，其性能受到事先选择的惩罚因子C和核函数(一般选择高斯核函数)参数γ的影响，这使得分类器性能无法自动达到最优状态。虽然传统网格遍历参数寻优算法能够实现参数的优化选择，但是计算量非常大，在实际的工程应用中具有很大的局限性。因此，文献[25]采用遗传算法寻优功能实现故障诊断。

针对小波基描述某种信号较好而对其他信号描述较差以及稀疏表示过完备字典原子的高冗余性，为了提高轴承故障诊断的自适应能力，本文提出了自适应紧框架学习方法用于故障诊断，这种紧框架由振动信号本身学习得到，因此可以很好地描述信号；然后通过训练得到的滤波器组对故障信号进行滤波，通过不同故障信号频率在不同滤波器下响应不同的原理构造特征；最后使用基于遗传算法优化的SVM分类器对故障信号进行分类。

1 故障信号分解的紧框架训练与信号去噪

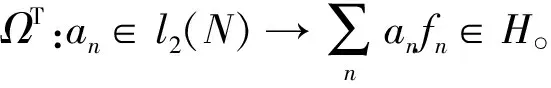
为了使紧框架能够对信号进行有效的描述和完全的重建，我们可以通过紧框架结构约束条件下的稀疏字典学习模型来实现[26],即通过求解如下最小化模型可以实现紧框架的构造

s.t.ΩTΩ=I

(1)

式中：y为振动信号；Ω(f1，f2,…,fr)为在紧框架下的分析算子；v为系数稀疏向量；上式第一项表示稀疏误差；第二项保证系数趋向稀疏；约束项ΩTΩ=I保证Ω是紧框架。由于这个最小化问题是高度非凸问题，且l0是一个NP难问题，因此采用l1范数最优近似l0范数，将非凸问题转化为凸问题：

s.t.ΩTΩ=I

(2)

1.1 优化方程求解

优化问题式(2)可以通过两个交替的子优化问题来实现。

步骤1稀疏编码

先用一个框架给Ω赋初值，则式(2)转化为

(3)

该问题可以通过阈值法求解

(4)

式中：HT为硬阈值算子;λ为事先确定的阈值。

步骤2字典更新

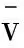
s.t.ΩTΩ=I

(5)

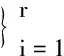
(6)

将系数向量均匀的分为r个向量，并将它们表示为vi∈RR×1,i=1,2,…,r。因此目标函数可以转化为

(7)

式中，yk,k=1,2,…，N取自信号y的r×1分量。

通过构造如下的矩阵

目标函数可进一步转化

(8)

式中，Tr(·)为矩阵的迹，则式(8)所表示的优化问题等价于

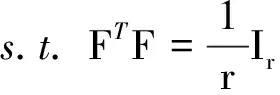
(9)

1.2 噪声去除与信号重建

在得到紧框架Ω之后就可以利用紧框架对原始信号进行分解，在每次迭代过程中将式(6)中的y换为阈值处理后的

为了说明紧框架的去噪效果，我们使用实测轴承振动信号(见图1)进行验实验证，实验信号来自于凯斯西储大学轴承数据中心。为了确保算法的适应性，实验选取四种状态信号，即正常信号、内圈故障信号、滚动体故障信号和外圈故障信号，信号长度为2 000点。从图可以看到正常信号幅值小，振动频率低；内圈故障信号和外圈故障表现出周期性、冲击性等特点；而滚动体故障幅值较小。经本文算法去噪后的信号，如图2所示。由于数据在采集过程中受到噪声等的干扰，导致信号去噪后会出现两种不良后果：一是不同故障信号在强噪声干扰下，去噪后故障状态难以区分；二是在弱噪声情况下，信号去噪后看不出去噪效果。针对第二情况，我们通过对去噪前后的信号分别做频谱图(见图3和图4)来观察去噪的效果。由于噪声是高频信号，因此考察去噪的效果，只要分析高频情况即可。对比图3和图4可以看出，去噪信号的高频成分已经含有很少的高频分量，同时幅度较大的故障特征频率及其谐频分量都很好地保留下来了，这说明本文的算法具有很好的去噪性能，即去噪效果明显。

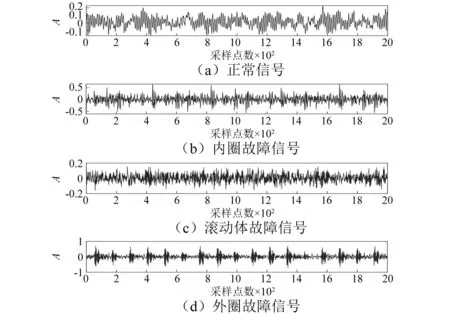
图1 四种不同状态的振动信号Fig.1 Vibration signals in four different states

图2 四种噪声滤除信号Fig.2 Four kinds of noise filter the signal

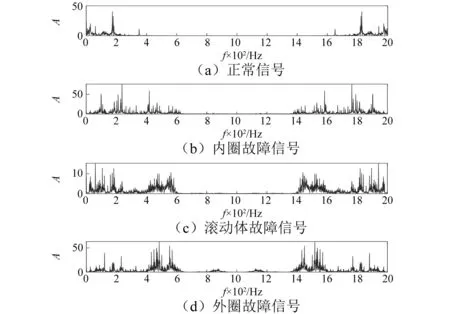
图3 振动信号去噪前频谱图Fig.3 Spectrum of vibration signal before denoising

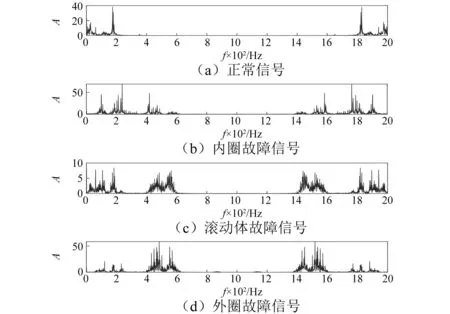
图4 振动信号去噪后频谱图Fig.4 Spectrum of vibration signal after denoising

2 故障模态的特征向量构造

2.1 故障特征构造

振动数据训练得到的紧框架Ω的每一列代表一个滤波器分量。因此如果将振动信号y携带的全部特征看成是分布在一个空间(Ω的列构成的空间)的话，那么每个滤波器就代表其中的一个子空间。因此Ω可以构成r个子空间，并且可以将y分解为r个子空间信号zq∈Rm×1,q=1,2,…，r，即

式中，m为信号分解后的长度。对卷积后的信号zq做变换,得到它的频谱DFT(zq)。由于紧框架的每个滤波器都是一个带通滤波器，且具有频率选择特性，所有的r个带通滤波器正好实现对振动信号整个频带的划分。每种故障都有一个故障频率fd，因此一定有一个zq信号的频谱所包含的频率分量fd的频谱幅值最大，而其余滤波器对该故障频率的幅频响应相对较小。利用不同子空间对相应故障频率的幅频响应不同的原理，使用滤波之后的频域能量信息就可以实现对各故障特征的构造。

2.2 故障特征描述

根据特征构造的原理，采用如下的策略来描述故障特征。考虑故障信号在谐波、噪声等扰动对振动信号幅频响应的影响，对故障信号特征设计如下的幅频响应函数

(10)

式中：A(i)为振动信号傅里叶变换之后的第i个点的幅频响应;M为计算幅频响应函数是所取的幅频点数范围(M的选取将在第4章给出)。图5是在每个滤波器滤波后求得幅频响应情况下对应的能量，振动信号在不同滤波器下的幅频响应呈现不同的幅值，例如正常信号在第1个滤波器滤波后保留了大部分的信号能量，因此可以认为第1个滤波器的信号代表了正常信号的特征；内圈故障信号在第7个滤波器下保留大部分能量，可以认为第7个滤波器的信号代表了内圈故障信号的特征；同样第20个和第18个滤波器信号分别代表了滚动体故障和外圈故障的特征。不同的特征信号对应的滤波器不一样，尽管有可能不同的故障信号对应某个滤波器的能量最大，但是，他们在其他滤波器上保留的能量是不一样的，因此特征向量还是不一样的。因此特征向量之间有着明显的区分度，从而可以通过分类器进行故障识别。

为了设计简洁而又具有故障区分度的特征向量，对每个故障信号，使用下式确定故障频率响应前几个最大值对应的子空间

(11)

为了描述可区分的故障特征，本文生成维数r的特征向量saq=[0,0,…,0]，初值为0，对于每个振动信号将前n个最大的Id分别放入saq对应位置上，此时实现了对故障模态特征的描述。

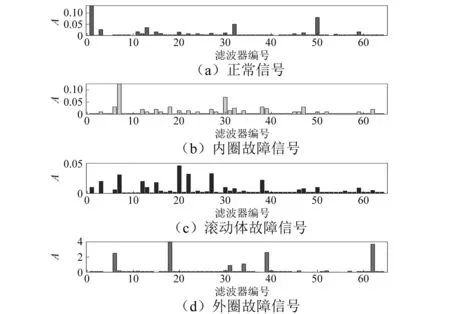
图5 不同滤波器对应Id值Fig.5 The corresponding Id value of different filters

3 基于遗传算法的SVM分类器参数优化

在得到振动信号的特征向量之后就可以用对其进行分类，但是SVM参数选取存在困难，因此本文采用遗传算法自动选取最优参数。将交叉验证下的个体错误率作为个体的适应度值,其具体表达式为

式中：yi为第i个样本的期望输出;Oi为分类器做出的预测分类输出；N为训练样本数。训练好数据后通过轮盘赌法来选择每次迭代中合适的个体即错误率低的个体，这一步骤要求选择个体的概率应该与个体的错误率成反比，这样每个个体被选择的概率为

式中：M为种群数；Fi为第i个个体的适应度。上式确保个体的适应度越大，被选择的概率会更高。为了产生新的个体，采用传统的实数交叉方式

式中：a为在[0,1]上的随机数；X1和X2为最初的两个个体；Y1和Y2为新的个体。变异操作是一种重要的产生新个体的操作，目的是影响算法的搜索方向。为了变异出新的个体，核函数参数变异采取如下方式

式中：f(g)=r2(1-g/gmax)，这里ri(i=1,2)是均匀分布在[0,1]内的随机数；amax和amin为个体上界和下界；g为目前迭代次数；gmax为最大迭代次数，即进化次数。

遗传算法优化参数C和γ的过程中，由于支持向量机进行分类的性能往往和惩罚因子C的选择有正相关关系，即C越大，分类器性能越好,变异操作让C趋向于变大的方向搜索。但并不是越大越好，在交叉操作中C也有可能变小，来平衡变异中C变大的趋势，这样可以让算法在总体上尽早收敛。

4 实验分析

本实验数据来自于凯斯西储大学轴承数据中心。选取滚动轴承的负载为0，轴承损伤直径为0.355 6 mm，轴承转速为1 797，采样率为12 kHz的正常状态、内圈故障、外圈故障和滚动体故障四种振动信号。在紧框架训练阶段，每种振动信号分别以滤波器个数为信号长度重叠截取足够多的样本，通过设置训练字典的参数(本文设置λ= 0.1)，得到较好的带通滤波器组。从每种振动信号中选取160个长度为2 048的信号作为测试数据，得到640个数据，其中480个用作训练集，160个用作测试集，测试样本顺序为：1～40为滚珠故障;41～80为内圈故障;81～120为正常状态;121～160为外圈故障。数据样本经第2章处理得到特征向量后使用遗传算法的优化分类器参数进行训练与预测。

4.1 滤波器数量对诊断率的影响

为了确定滤波器数量对诊断正确率的影响，首先将滤波器数量固定在较大值128个，来测试点数M和特征向量取前n个最大值对诊断率的影响，表1列出了不同M和n情况下的正确率，可以看出n在取2和3时已经达到很高的正确率，为了提高特征的区分度，选择n=8，考虑到故障信号的特征频率在60～200 Hz，且存在噪声及各种扰动，选择M=550，本文以下的实验均采用同样的数值。不同滤波器数量情况下的诊断正确率,如表2所示，可以看出在滤波器数量为32时，训练集和测试集的分类正确率已经很高，且在滤波器数量增加到64时，即信号频域子空间分解的更多更细的时候，信号特征频率的响应会更加突出，因此诊断率会继续增加。为确保诊断率和训练测试时间之间的平衡，选择滤器数量为64。

表1 不同M值和n值情况下诊断正确率(训练集/测试集)Tab.1 Diagnostic accuracy under different M values and n values(training set/test set) %

表2 不同滤波器数量诊断准确率Tab.2 Diagnostic accuracy of different filter numbers

4.2 遗传算法与SVM参数

图6为遗传算法迭代次数与正确率关系图，可见20次迭代后即可处于一定的稳定状态，参数C和γ参数如图6所示，迭代最高正确率接近100%。本文使用的遗传算法参数如表3所示。

图6 遗传算法优化SVM过程Fig.6 The genetic algorithm optimizes the SVM process

表3 遗传算法与SVM参数Tab.3 Genetic algorithm and SVM parameters

4.3 实验结果

图7展示了本文提出的自适应紧框架训练的方法对振动信号测试集的诊断正确率达到100%，说明本文方法可以很好地实现故障诊断。以同样的数据用连续小波尺度能量(continuous wavelet dimension energy,CWTDE)、小波包能量特征(wavelet package energy,WPE)方法、稀疏表示方法(sparse representation,SR)和经验模态分解方法(EMD)提取轴承振动信号特征。诊断结果如表4所示，可以看出本文方法比连续小波尺度能量方法和稀疏表示的方法对轴承振动信号的诊断正确率有较大的提高；本文方法相比于经验模态分解方法有一定的优势，本文构造的紧框架自适应能力较好；本文方法略优于小波包能量特征方法，但它可以根据振动信号本身构造紧框架从而自适应解决轴承故障的诊断问题。

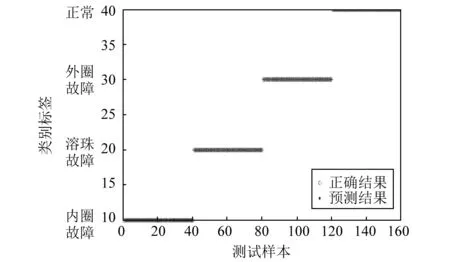
图7 四种类别测试集正确率Fig.7 The accuracy of the test set of four categories

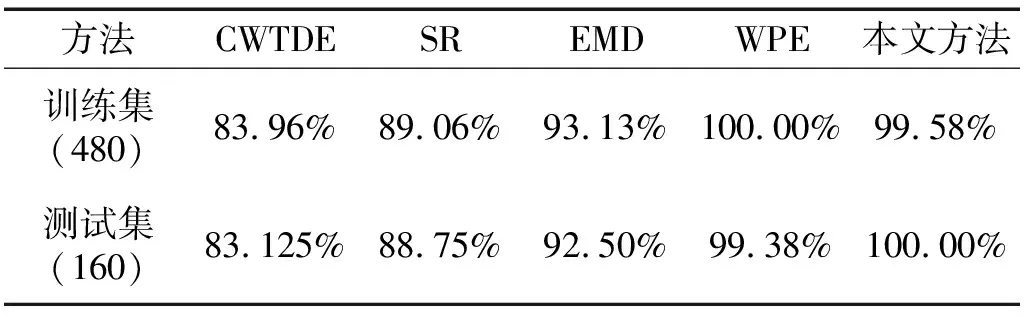
表4 不同方法在DE12000数据上诊断正确率Tab.4 The diagnostic accuracy of different methods on DE12000 data

本文另外使用西储大学数据库中采样率为48 kHz的驱动端数据(简称DE48000)说明本文方法的优势。其实验结果如表5所示。本文方法在DE48000数据表现出比其他方法的优势，而其余几种方法正确率有所下降，本文方法由于基于数据自身训练自适应能力较强获得了较好的结果。

表5 不同方法在DE48000数据上诊断正确率Tab.5 The diagnostic accuracy of different methods on DE48000 data

为了进一步说明本文方法可以很好地解决轴承故障诊断问题，将三种故障数据按照故障深度分别划分，来说明在识别了故障种类的情况下，本文提出的方法在识别同种故障的故障深度的有效性。得到内圈故障、滚珠故障和外圈故障的数据，其中每个类别每个故障深度的样本都为80个,即每组共有数据240个，训练和测试样本数占比为3∶1。在相同样本下与其他几种方法对比得到测试集正确率，如表6所示。在故障类型细分情况下，CWTDE、SR和EMD方法在识别滚动体故障深度时表现较差，而对于内圈故障深度和外圈故障深度的识别率有所提高。由表可以看出，本文方法和WPE方法在识别同种故障不同故障深度时，可以达到很高的正确率。因此本文提出的方法可以很好地确定轴承故障种类以及故障轴承具体损伤的直径。

表6 故障细分时不同方法诊断准确率Tab.6 The diagnosis accuracy of different methods is different in fault subdivision

5 结 论

本文提出了一种基于自适应紧框架学习的滚动轴承故障诊断算法，利用滚动轴承故障数据集进行紧框架训练，得到可以完全重建原始信号的紧框架，信号经紧框架分解后去除较小的稀疏系数达到去噪效果；振动信号通过紧框架滤波器组的滤波操作得到信号某些特定的频带信息，统计其频谱部分能量来构造振动信号特征向量，通过遗传算法分类器实现轴承振动信号的正确诊断。本文克服了小波方法无法自适应描述轴承故障信号的缺点。仿真实验表明，本文方法在振动信号诊断问题上具有很强的鲁棒性。