张力腿平台局部系泊失效下复杂运动响应机理研究

成司元， 余 杨， 余建星， 郝 帅， 吴静怡， 张春迎， 康煜媛

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.高新船舶与深海开发装备协同创新中心，上海 200240；3. 中国石油管道局工程有限公司 天津分公司，天津 300457)

张力腿平台(tension leg platform，TLP)是一种垂直系泊的顺应式平台，一般由平台主体(甲板、立柱、浮箱)、系泊系统和锚固基础三部分组成[1]。通过自身结构产生远大于重力的浮力，浮力除了抵消自质量外，剩余浮力与筋腱提供的预张力平衡。较大的筋腱预张力使平台平面外的运动(垂荡、橫摇和纵摇)较小，近似于刚性。同时，张力腿平台及其系泊系统是一个非线性系统，在某些极端海况作用下可能发生部分张力筋腱的失效，从而改变整个结构的固有频率，同时系统回复力也会受到较大影响，非线性部分作用会被放大，平台响应的幅值增大且改变运动规律，危及筋腱失效后平台生存能力。

张力腿平台主体与系泊系统是一个相互耦合的动力系统，国内外学者大部分都是通过时域分析研究TLP平台的运动响应。印度理工学院的Ahmada等[2]研究了TLP在随机波浪谱下的耦合响应，考虑了水动拖曳力、可变张力、可变浸水、长期偏移和波动风载荷耦合效果引起的各种非线性效应。印度理工学院的AK Jain[3]采用确定性的一阶波浪力来分析TLP的动态响应，考虑6自由度的耦合、非线性的张力变化及水动力的影响。Adrezin等[4]研究了单柱张力腿平台与张力腿的耦合动力响应,把张力腿简化为非线性梁结构,并仅考虑平台纵荡和垂荡两个自由度。Low等[5]利用集中质量法，在时域内研究浮式生产船与其系泊系统的耦合关系。刘应中等[6]计算了风浪流联合作用下系泊系统的响应特性。黄祥鹿等[7]通过建立二阶摄动方程，求解出考虑与系泊系统动力耦合的平台主体结构的二阶慢漂运动。

上述都是针对完整系泊系统分析的，但深海作业环境复杂，由于疲劳损伤、人为错误操作、意外碰撞等原因导致系泊系统部分筋腱失效。国内外学者对筋腱失效的响应也展开了研究，Mansour等[8]分析了典型TLP平台在筋腱完整、筋腱移去和筋腱破裂后在100年、1 000年和10 000年极端海况下的生存能力。Kim等[9]通过比较筋腱失效后运动轨迹和剩余筋腱的张力，研究了一根和多根筋腱失效后在中等海况下的TLP动态稳定性和生存能力。Yang等[10]分析筋腱失效对运动响应、筋腱和立管张力的影响，并且对比了筋腱底部失效和顶部失效的影响。Yu等[11]对比在极端海况下不同数量筋腱同时失效和多根筋腱连续性失效对平台运动响应和筋腱张力的影响。上述学者主要观点是筋腱失效后，平台瞬态响应的特点，然而，对于不同数量筋腱失效后对运动响应的影响及筋腱失效后的结构的复杂运动响应机理很少涉及到。

本文通过数值模拟的方法，建立了平台主体-筋腱非线性耦合模型，在一阶规则波下研究单根和两根筋腱初始时刻失效的时域响应全过程，对筋腱失效位置、失效组合对平台系统固有特性及运动响应的影响进行研究；并分析筋腱失效对平台复杂运动响应的影响，探究其发生机理。

1 数值模型

本文基于ANSYS®AQWATM软件进行张力腿平台的水动力建模分析。一个完整的TLP数值计算模型包括面元模型、莫里森模型和筋腱模型三部分，平台参数见表1。

1.1 面元模型

面元模型用来描述平台的湿表面，通过水线面将平台划分为水上和水下两个部分，然后对平台进行网格划分。本文共划分了8 878个面单元，其中包括绕射单元3 623个，见图1。在频域分析中，通过基于面元模型的计算可获得入射力、绕射力以及附加质量和辐射阻尼等。

表1 TLP平台的主要参数

图1 面元模型Fig.1 Panel model

1.2 莫里森模型

面元模型在参与水动力计算时忽略了水的黏性，为了补偿数值模型水的拖曳力，8个莫里森模型分别应用到TLP的4个立柱和4个浮箱上，见图2中结构内部的黑线。

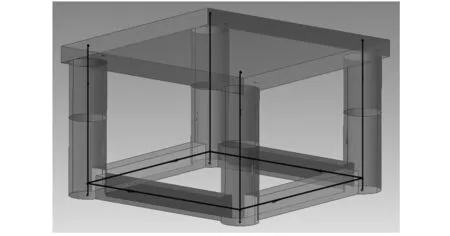
图2 莫里森模型Fig.2 Morision model

1.3 筋腱模型

本文采用Tether单元模拟TLP系泊系统，见图3中的8根筋腱。该筋腱模型是柔性细长杆件且直径与波长的比值很小。Tether模型两端设置为端部固定，允许Tether模型有轴向的拉伸，不允许有绕轴向的扭转运动。

图3 筋腱模型Fig.3 Tendon model

2 理论方法

2.1 三维势流理论

本文采用的海洋环境了一阶规则波(Airy波)，它基于以下假设：流体均质不可压缩且无黏无旋、波幅与波长和水深相比是小量。因此，由于入射、绕射和辐射波产生的势可以写成

(1)

式中：φI为单位波幅下的一阶入射波浪势；φd为与之对应的绕射波浪势；φrj为第j个自由度由于单位幅值运动产生的辐射波浪势。

已知波浪速度势，一阶流体动压力分布可以通过线性化的伯努利方程求得

(2)

根据压力分布对平台湿表面的积分，可以得到各种流体力。

由于入射波产生的第j自由度上的Froude-Krylov力为

(3)

由于绕射波产生的第j自由度上的绕射力为

(4)

由于第k个自由度的单位幅值的刚体运动产生的辐射波在第j个自由度上产生的辐射力为

(5)

所以，总的一阶水动力可以写成

(6)

式(6)是基于势流理论计算出的流体水动力，它主要针对的是大型浮体，忽略了水的黏性效应。

2.2 筋腱模型理论

本文采用Tether模型来模拟筋腱，一个Tether单元受到的合力Fe包括

Fe=Fk+Fs+Fi+Fm

(7)

式中：Fk为由于结构弯曲刚度引起的内力；Fs为由端部节点处的弹簧施加的外部力；Fi为由重力、流体静力、拖曳力、波浪惯性力、Froude-Krylov力和抨击力组成的积分合力；Fm为固结在筋腱单元上的随动坐标系的惯性力。

筋腱的拖曳力和波浪惯性力是基于莫里森理论计算而得的，莫里森理论广泛应用于直径小于1/5最短波长的细长杆件。

(8)

式中：拖曳力系数Cd为1.1；惯性力系数Cm为2.0；uf为水质点的水平速度；us为结构的水平速度。

2.3 时域运动方程

浮体在时域中的运动方程可以通过卷积的形式来表示

(9)

式中：m为结构的质量矩阵；A∞为在无限频率下的流体附加质量矩阵；C为由于绕射单元产生的除了线性辐射阻尼在内的阻尼矩阵；K为总的刚度矩阵；h为加速度脉冲函数矩阵，其表达式为

(10)

式中，Aω和Bω分别为与频率有关的附加质量矩阵和水动力辐射阻尼系数矩阵。一般地，附加质量系数在零频率和无穷频率下的值为零，所以使用式(10)中的附加阻尼系数矩阵来获得的脉冲响应函数矩阵更为实际。

3 模型验证

本文研究的张力腿平台来源于Gie和Boom做的缩尺比实验，另有17家研究机构对此平台进行了频域分析。时域结果是由频域分析结果直接决定的，因此本文对频域分析结果进行了比对。为了保证数值算法的准确性，通过AQWA中的Additional Hydrostatic Stiffness功能，将8根系泊系统对平台的影响放进了频域计算结果当中，结果见图4～图6，由于内容有限，只放了部分对比图片[12]。

从图中可以看出，在筋腱完整的情况下，无论是平台运动的RAOs和附加质量、辐射阻尼，还是平台承受的波浪载荷，都与17所研究单位的试验结果吻合得很好，从而证明数值算法的正确性。因为筋腱完整时的数值算法的准确性通过了验证，通过AQWA自带的Suppress的功能，抑制住一根或两根筋腱，从而达到筋腱失效的数值算法也是正确的。

筋腱失效的具体步骤为：①先在时域内计算8根筋腱完整时的平台水动力计算；②提取上一步中失效筋腱对平台的作用力历程；③保持其余筋腱的情况不变，抑制住失效筋腱的作用，施加失效筋腱从开始到失效时刻这段时间内对平台的作用力历程；④进行水动力计算，得到瞬态和稳态的时间历程响应。

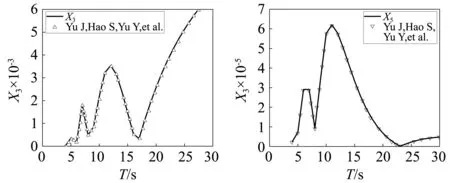
图4 垂荡、纵摇在0°浪向下的RAOsFig.4 Heave and pitch RAOs for wave at 0°

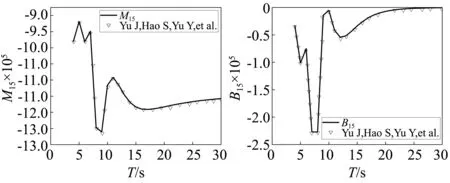
图5 纵摇的附加质量系数和辐射阻尼系数Fig.5 Add mass pitch coefficient, damping

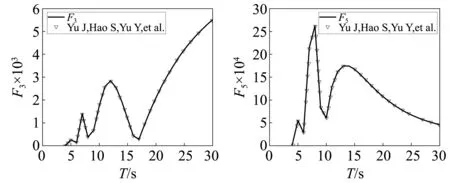
图6 垂荡、纵摇在0°浪向下的波浪力Fig.6 Heave and pitch wave force for wave at 0°

4 计算结果及分析

根据以往研究可知，一根筋腱断裂，相连的筋腱在很短的时间内也可能断裂，当发生连续断裂时，由于时间差很小，可以认为两根筋腱是同时断裂的。因此，本文选取#1筋腱失效和#1#2筋腱同时失效，分别对筋腱失效后的复杂运动响应进行分析。

在施加波浪载荷进行时域分析之前，先对筋腱完整和筋腱失效情况下平台自身的振动特征进行研究，图7给出平台筋腱的示意图。

图7 筋腱分布图Fig.7 Layout of tendons

4.1 固有振动特性分析

4.1.1 固有频率和阻尼比

为了得到筋腱完整和失效后的平台固有振动特性，需要对平台进行自由衰减测试，本文在分析的过程中发现(见图8和图9)：筋腱失效后，虽然在纵荡方向上会有一个瞬态位移的改变，但由于其位移改变量相对于筋腱长度来说是一个极小量；筋腱失效的瞬间，系泊系统对平台的纵向分量虽然会有瞬态的增大，但对纵荡的影响不大，纵荡会根据平台及其系泊系统的布局重新到达新的平衡位置，而且系泊力的纵向分量比垂向分量小了3个数量级。因此，本文重点是针对筋腱失效后垂荡运动响应的分析，所以对垂荡运动特性进行了一系列的测试，根据衰减曲线得出响应的固有振动频率和阻尼比，表2给出测试结果。

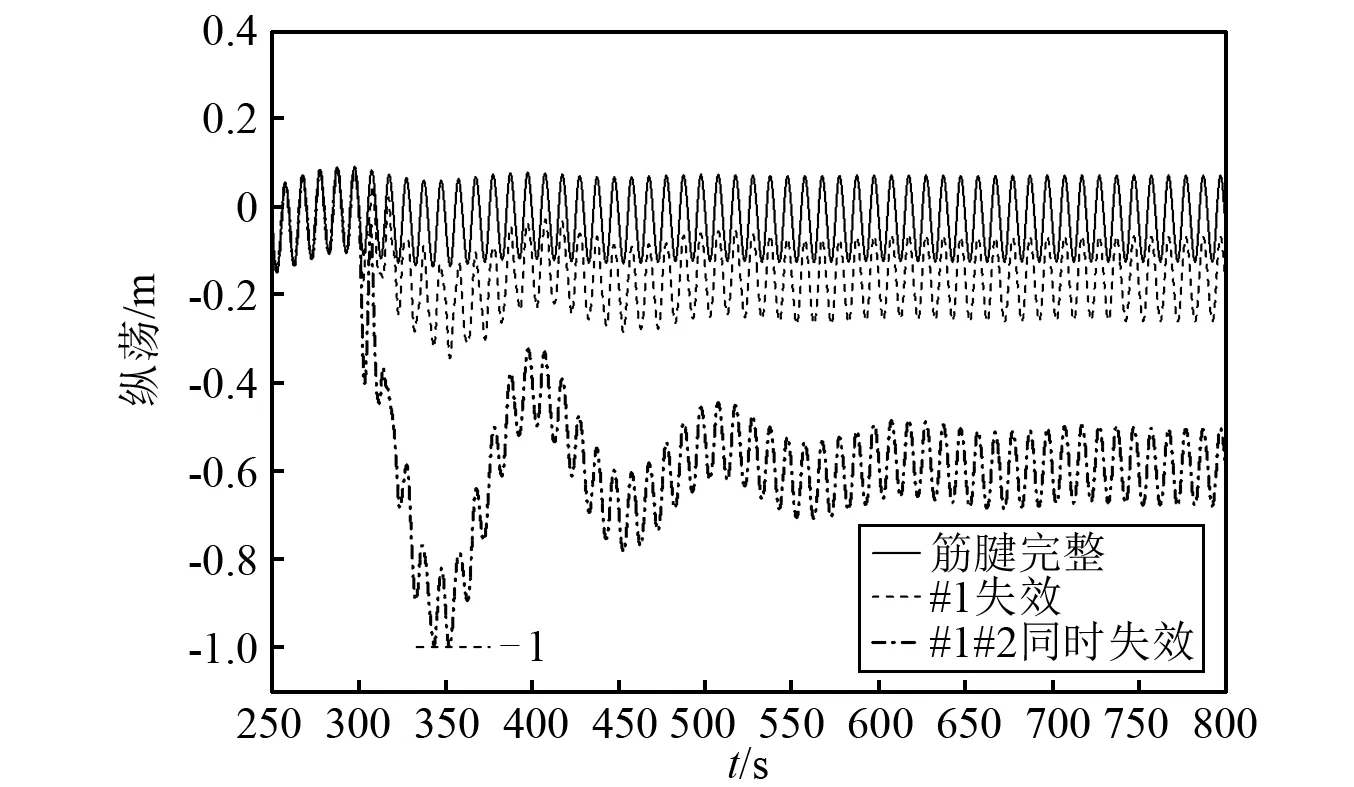
图8 筋腱失效后的纵荡瞬态响应Fig.8 The surge transient response after tendon failure

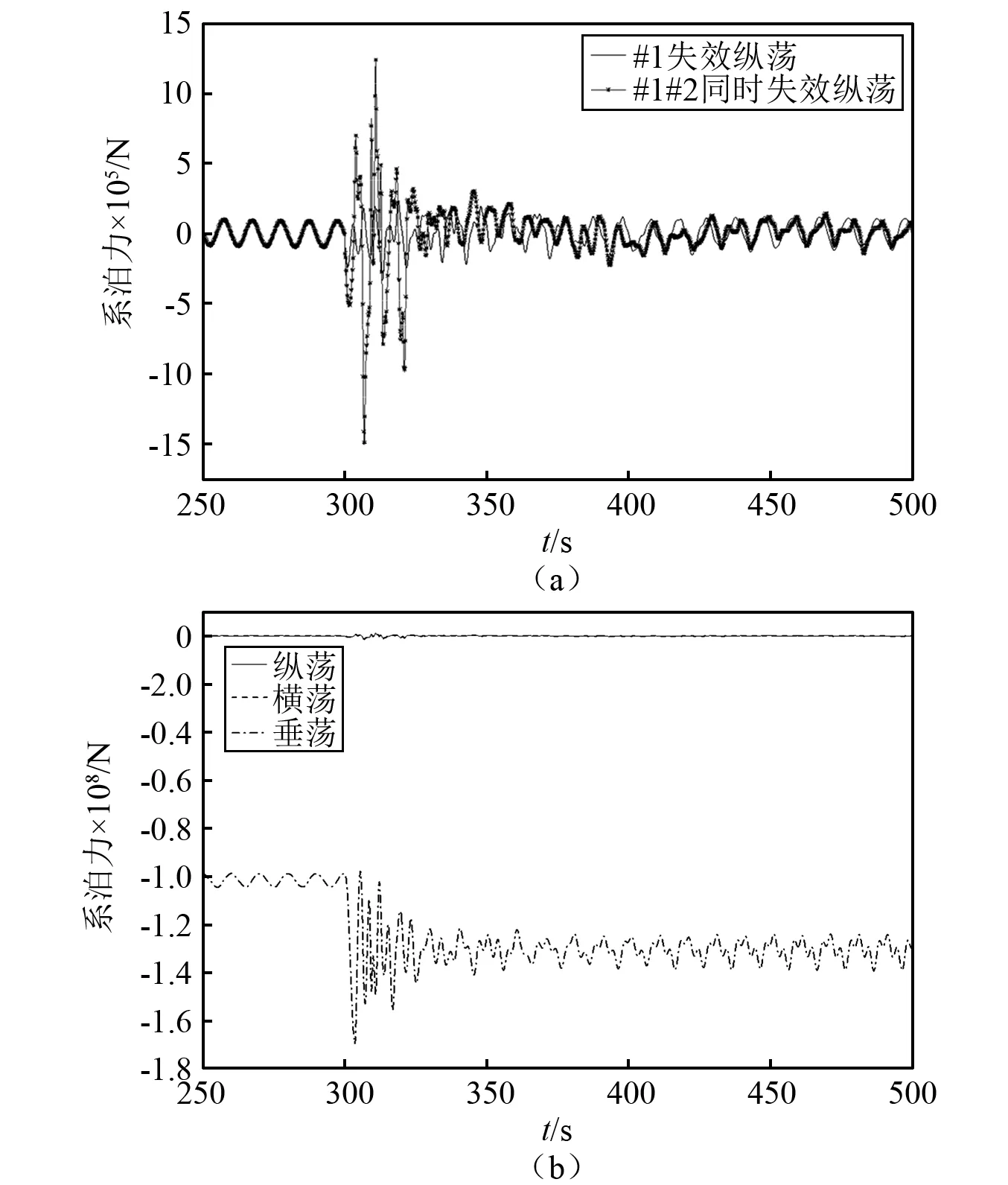
图9 筋腱失效后纵荡和垂荡系泊力响应Fig.9 The surge/heave mooring force response after tendon failure

表2 平台垂荡固有频率和阻尼比

从表2可知，虽然筋腱失效数量不同，但平台垂荡固有频率较筋腱完整时都有所下降，#1#2筋腱同时失效的垂荡固有频率下降了约45%，#1筋腱失效的垂荡固有频率下降了约16%。

表2中还可以发现阻尼比呈现先下降后上升的趋势，究其原因为：当只有#1筋腱失效时，稳态的运动幅值与筋腱完整时运动的稳态幅值相近，但单根筋腱的缺失会导致莫里森拖曳力减小，从而降低阻尼比；当#1#2同时失效时，虽然莫里森拖曳力减小，但整个平台的运动幅值大幅度上升，使得势流阻尼大幅度提高，且势流阻尼的增加量大于莫里森拖曳力的减小量，最终使整个平台的阻尼比上升。

4.1.2 刚 度

影响平台运动的另外一个重要因素就是刚度，因此对筋腱失效后刚度的测量很有必要，图10展示了筋腱不同状态下的刚度曲线。

刚度的改变与固有频率类似，#1#2筋腱同时失效的刚度较筋腱完整时下降了约45%；#1筋腱失效较筋腱完整时刚度下降了约16%。

从平台固有特性分析中可看出结构刚度与固有频率的变化幅度保持一致。究其原因是由于剩余筋腱的预张力重新分布，平台吃水减小，静水力下降，再加上筋腱数量的减少，最终导致刚度下降，直接影响平台的固有频率。局部系泊失效后不同立柱下筋腱张力分布不同，平台也可能发生小角度倾斜，因此需要对不同失效状态下平台的平衡位置展开进一步分析。

图10 筋腱分布图Fig.10 Curves of stiffness

4.1.3 静水分析

本文采用一阶规则波作为环境载荷，忽略了包括漂移力在内的所有二阶力的影响，因此分析平台在环境载荷中的平衡位置可以转化为分析平台在静水中的平衡位置，图11给出了筋腱失效后平台垂荡的平衡位置。

图11 垂荡平衡位置对比Fig.11 Comparison of heave balance position

从图11中可知，#1筋腱失效后平台垂荡的平衡位置较筋腱完整时提高了20.2%，#1#2筋腱同时失效时垂荡平衡位置提高了93.6%。将垂荡平衡位置改变与刚度对比可以发现：平衡位置的改变明显大于刚度的改变；通过对筋腱张力的分析可以发现(见图12)，虽然平台总预张力下降了一小部分，但因为平台静水力减少，使平台整体吃水变小，再加上某些立柱上的筋腱张力改变较大，导致平台旋转产生不可忽略的倾斜角，由于旋转中心并不在重心位置，所以重心会绕旋转点产生额外的垂向位移。

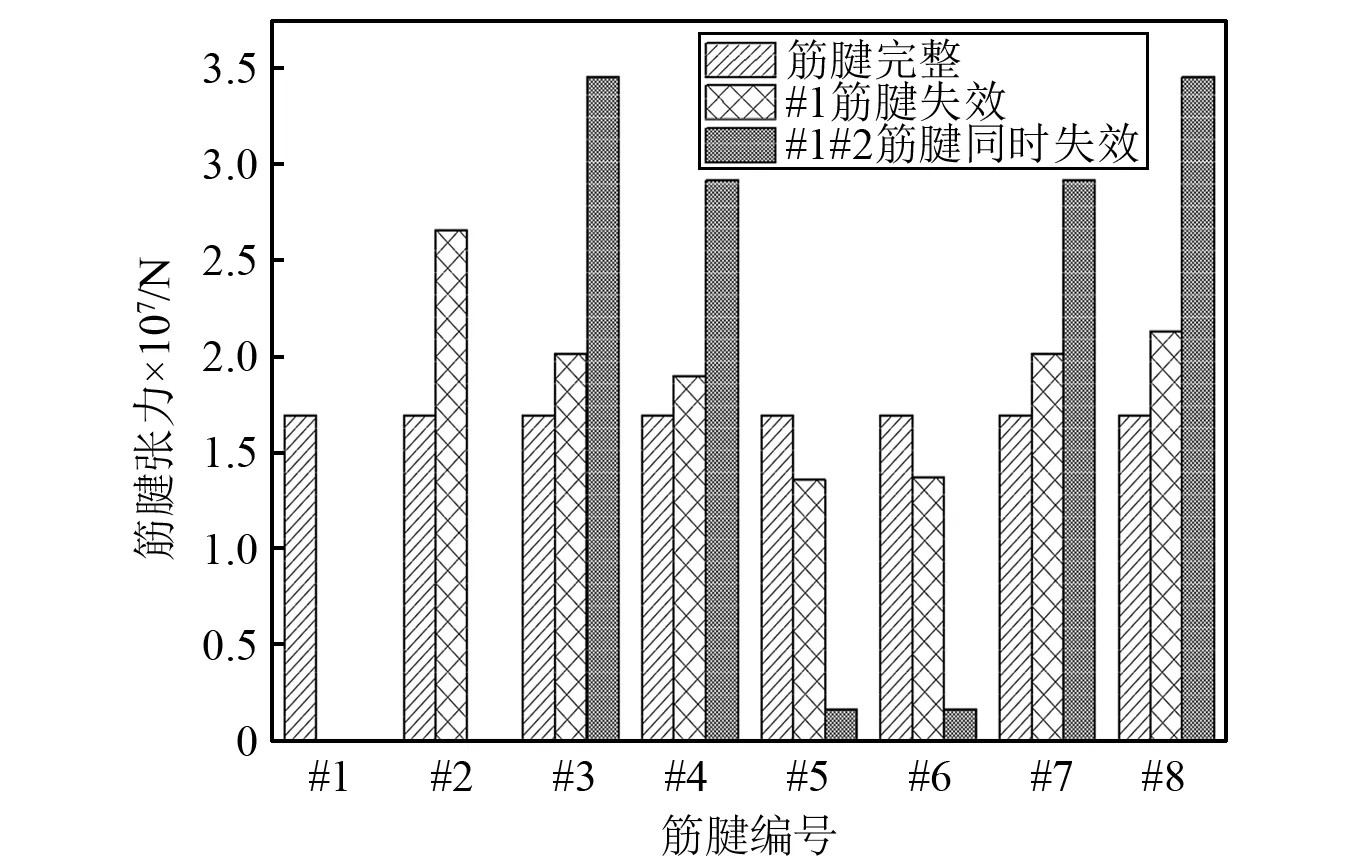
图12 各筋腱张力Fig.12 Tension of each tendon

根据对张力的分析，可以认为平台在筋腱失效后经历了两个过程：第一个过程是筋腱失效后，损失的预张力平均分配给剩余筋腱，是平台产生垂向的平移；第二个过程是由于筋腱张力不对称，会产生力矩，是平台绕某个轴转动，在这个过程重心也会有垂向运动，见图13。经过计算，#1筋腱失效的情况下，转动引起的重心垂向位置的改变约占垂向总位移的3%；#1#2筋腱同时失效的情况下，转动引起的重心垂向位置的改变约占垂向总位移的20%。

图13 平台静水平衡图Fig.13 Balance position of TLP in calm sea

4.2 运动响应分析

4.2.1 振幅分析

本小节将会基于静水分析研究波浪载荷下平台的运动响应，涉及运动的平衡位置、幅值以及结构非线性。平衡位置在4.1节中已进行充分的分析，本节不做过多赘述。

首先介绍本文采用的环境载荷为周期10 s波高4 m的Airy波，浪向为0°(与X轴正向夹角为0°)，之所以选取此环境载荷，是因为在此环境载荷下剩余筋腱依然能保持良好的工作能力，不会使剩余筋腱出现负张力，进而发生屈曲现象。筋腱失效后的静水平衡位置作为平台水动力分析的初始位置，计算出的运动响应见图14。

图14 垂荡运动响应图Fig.14 Motion response of heave

从图14中可以清晰的发现，在环境载荷作用下，平台垂荡平衡位置和静水中基本相同；#1筋腱失效的平台垂荡幅度较筋腱完整时增大了约30%，#1#2筋腱同时失效的平台垂荡幅度较筋腱完整时增大了约2.7倍。图14中显示了筋腱完整和#1筋腱失效两种情况下的垂荡运动响应呈线性特点(简谐振动)，而当#1#2筋腱同时失效后垂荡运动响应中出现了大量高频成分。

对于筋腱完整和#1筋腱失效的情况，其稳态振幅可以根据有阻尼强迫振动稳态幅值计算方法得出

A=ystαd

(11)

式中：A为运动的振幅；yst为动载荷幅值作用下引起的静位移；αd为动力放大系数。

虽然#1#2筋腱同时失效后的垂荡响应呈现非线性，但是其运动响应可以认为是多种频率不同的规则响应的叠加，因此，其波频下的运动幅值仍然可以根据上述公式进行计算，计算结果见表3。

从表3中可以看出，对于三种不同系泊状态，根据线性动力学计算出的理论幅值和数值求解波频幅值基本吻合。TLP平台及其系泊系统本身是一个复杂的非线性系统，但对于筋腱完整和#1筋腱失效两种系泊状态，线性部分在垂荡运动响应中占主导作用，非线性并不明显，因此大多数情况下把该弱非线性系统作为线性系统考虑。然而，当#1#2筋腱同时失效后，环境载荷激发出结构自身非线性部分的响应，使实际垂荡幅值远大于线性部分产生的幅值。从图15中可以看出，垂荡响应中出现了二倍频和三陪频的响应，分别为波频响应的25.9%和30.9%。

表3 计算出的理论波频幅值

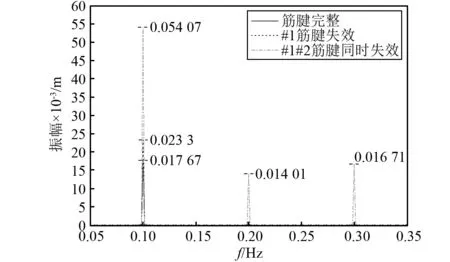
图15 垂荡频谱分析Fig.15 Heave spectrum analysis

4.2.2 非线性分析

本小节主要针对#1#2筋腱同时失效后运动响应的非线性展开分析。非线性振动系统的主要特点：系统的回复力是系统空间位置的非线性函数，而阻尼力是系统运动或振动速度的非线性函数，研究非线性主要是找出运动方程中的非线性成分。张力腿平台的回复力由静水回复力和系泊力共同提供，但由于平台自身的回复刚度与系泊线的刚度差了两个数量级，所以系泊系统提供的回复力是平台回复力的主要来源；系统的阻尼力由辐射力和莫里森拖曳力提供，图16给出了运动过程中受到的部分力的时间历程。

从图16的计算结果可知，相较于其它两种力，莫里森拖曳力的量级较小，对平台运动影响较小；图16(a)可以看出垂荡运动响与辐射力同步，垂荡响应的峰值与谷值和辐射力的峰值与谷值一一对应；系泊系统作为外力作用，从图16(c)可以看出，虽然运动响应和系泊力同步，但运动的幅值与系泊力的谷值一一对应；从系泊力时间历程曲线可以发现，虽然结构的静刚度(静水中分析出的刚度)呈现线性的特点，但由于外部载荷的影响，使系泊系统中各筋腱受到随时间不同变化的外力，最终导致结构的动刚度呈现非线性。

为了更直观的观察张力腿平台在筋腱失效前后的非线性影响，图17和图18展示了平台运动的相图和庞加莱映射图。

两幅图中可知，当筋腱处于完好的情况下，庞加莱截面上只有一个点，因此平台垂荡为周期运动；当#1筋腱失效的情况下，相图分析表明平台垂荡依然为周期运动，线性部分处于支配地位，非线性因素看作对线性振动的干扰；当#1#2筋腱同时失效的情况下，从庞加莱截面上可以发现有3个相点，因此平台垂荡为3周期运动。

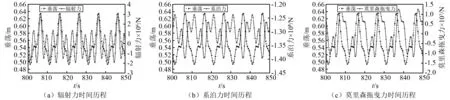
图16 平台各力时间历程Fig.16 Response of different forces

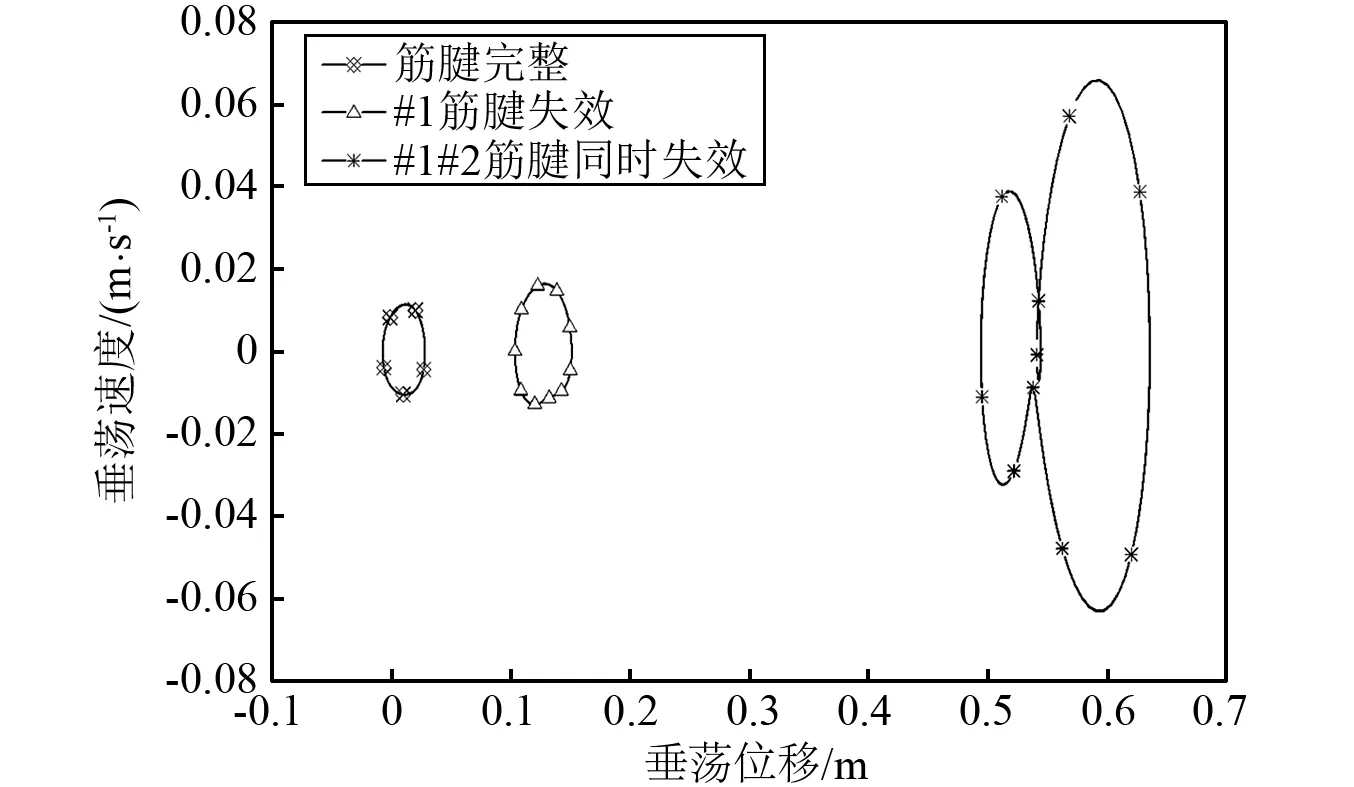
图17 波高4 m下的垂荡相图Fig.17 The heave phase diagram at a wave height of 4 m

为了更深入的理解平台在#1#2筋腱同时失效下的非线性特点，本文通过改变波高(用H表示)来观察平台高频响应的变化规律，见图19和图20。

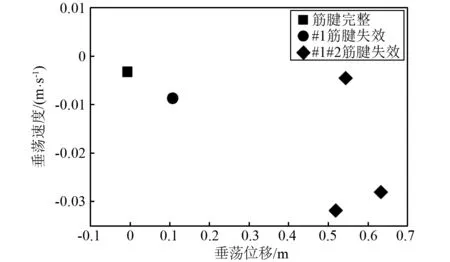
图18 波高4 m下的垂荡庞加莱映射图Fig.18 The heave Poincare mapat a wave height of 4 m

图19可知，当波高为1 m时，平台垂荡相图为一个圆圈，平台的垂荡运动表现为线性特点；当波高为2 m时，平台垂荡相图出现了局部凹陷的现象，二倍频响应出现，但垂荡运动依然为周期运动，非线性部分只能作为对线性响应的微小干扰，原因为当波高为1 m或2 m时，波浪能量较小，不足以完全激发出平台的高频响应；当波高为3 m时，平台垂荡相图发生了较大变化，非线性部分开始明显，二倍频成分增加，三倍频成分激增，垂荡响应曲线明显出现非线性部分，平台开始做多周期运动；当波高为5m时，平台垂荡相图较波高为4 m时非线性部分更加明显，非线性部分的轨迹线对线性部分轨迹线的影响加强，平台做3周期运动，原因为垂荡运动方程稳定解中的高频分量为波高的高次方，随之波高的增加，高频响应的幅值会呈现幂次增长。

图19 不同波高下的相图Fig.19 Phase diagrams at different wave heights

图20为不同波高下垂荡运动的频谱分析，本图再次说明，当波高较小时，二倍频和三倍频的振幅较波频振幅可以忽略不计；从图中还可以定量地分析平台高频响应的变化规律,根据Lagrange插值法，拟合出二倍频和三倍频幅值与波高的函数关系

A(2)=2.275 62×10-4H2+

0.002 69H-5.415 3×10-4

(12)

A(3)=-4.563 45×10-4H3+

0.004 69H2-0.008 61H+0.005 12

(13)

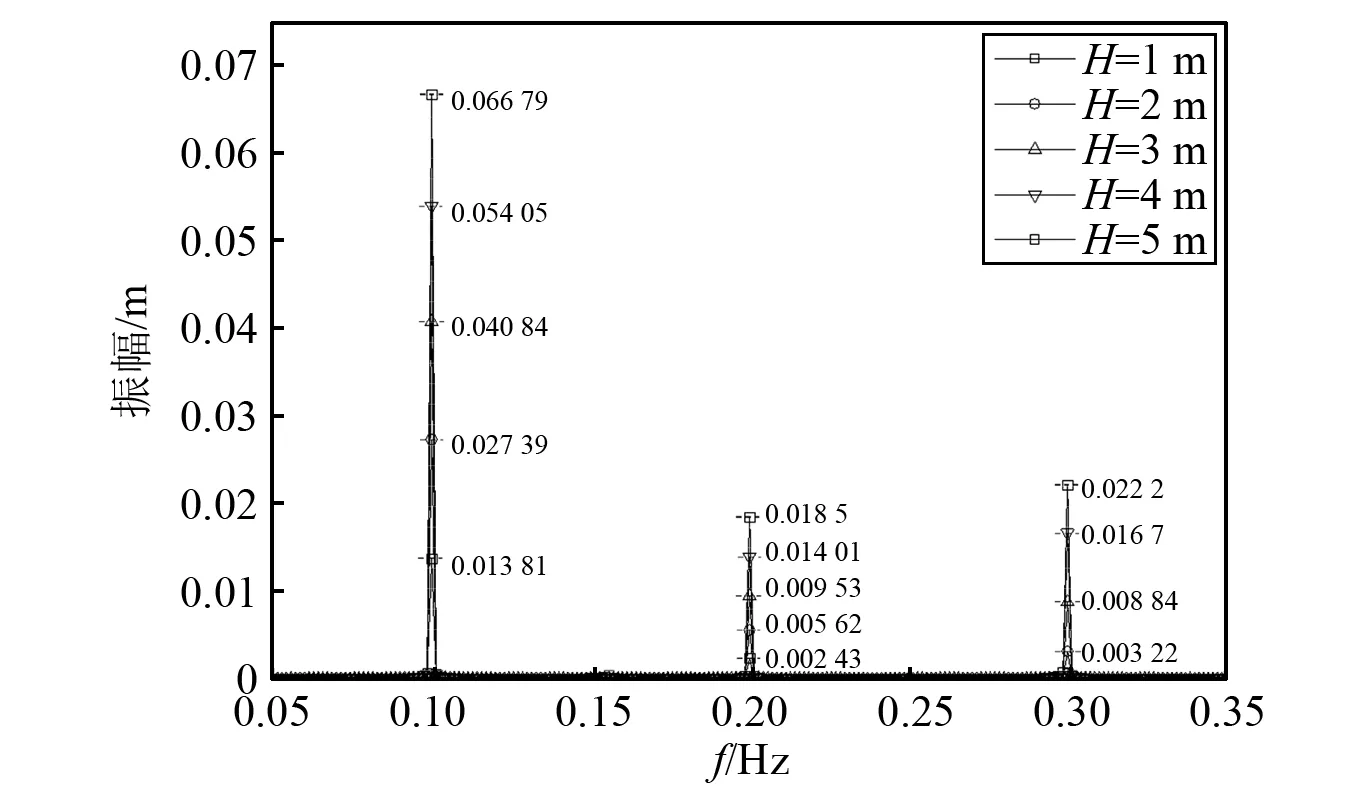
图20 不同波高下的运动频谱分析Fig.20 Analysis of motion spectrum at different wave heights

从方程式中可以直观的了解到，二倍频振幅含有波高的二次方，三倍频振幅含有波高的三次方，但由于系数比较小，只有波高足够大时，高频成分才能体现出来。从图中也能发现随着波高的增长，三倍频增长的速度明显快于二倍频增长的速度。

下面将对不同波高下该平台系统的回复力进行研究。图21为不同波高下辐射力和系泊力的频谱分析。由图可知，当波高为1 m时，辐射力和系泊力以波频幅值为主，二倍频和三倍频幅值较小，对波频运动的影响可以忽略；当波高为2 m时，辐射力的三倍频幅值超过波频和二倍频幅值，系泊力的三倍频成分开始占主导地位，但由于系泊力的波频幅值比辐射力的高频幅值大了一个量级，使平台依然表现为波频响应；当波高为3 m时，辐射力的三倍频幅值约为波频和二倍频幅值的2倍，系泊力的三倍频幅值与波频幅值接近，因此平台垂荡响应中三倍频成分出现；当波高为4 m，辐射力的三倍频幅值分别约为波频和二倍频幅值的3倍和2.5倍，系泊力的三倍幅值约为二倍频的3倍，导致平台的三倍频响应幅值超过二倍频。从频谱分析的整体走势可以发现，系泊力的波频幅值比辐射力的波频幅值大了一个数量级，两者的二倍频的幅值大约呈现二分之一的关系，系泊力的三倍频幅值大约为辐射力三倍频幅值的2.4倍。因此，本文认为平台的波频运动受系泊系统的影响较大，高频运动由辐射力和系泊力共同作用。

图21 不同波高下辐射力和系泊力的频谱分析Fig.21 Spectrum nalysis of radiation forces and mooring forces at different wave height

5 结 论

本文以一座带8根筋腱的典型张力腿平台为研究对象，通过数值模拟的方法，对局部系泊失效后的张力腿平台在规则波下的复杂运动进行了分析，主要结论如下：

(1)在一阶规则波作用下，平台的平衡位置与静水中大致相同，平衡位置的改变主要由预张力和刚度的减小量共同决定；平台固有频率随着筋腱失效数量的增加而降低。

(2)当筋腱完整或#1筋腱失效时，在0°浪向下的垂荡响应可视为线性响应；当#1#2筋腱同时失效时，平台的运动响应中出现了二倍频和三倍频非线性成分。

(3)在#1#2筋腱失效的情况下，当波高较小时，平台做近似简谐运动，非线性部分作为对线性运动的干扰，相图中只有一个极限环；当波高较大时，相图出现多个极限环，平台做多周期运动，二倍频幅值与波高存在二次方的关系，三倍频幅值与波高存在三次方的关系。

(4)辐射力和系泊力对平台的非线性响应影响最大，辐射力和系泊力的非线性决定了平台运动的非线性，从数量级来看，辐射力主要影响平台的三倍频响应，系泊力影响波频和三倍频响应，二倍频响应受到辐射力和系泊力的共同作用。