张力腿平台局部系泊失效模式下动力响应分析

余建星，高晓东，余 杨，郝 帅，徐立新



张力腿平台局部系泊失效模式下动力响应分析

余建星1, 2，高晓东1, 2，余 杨1, 2，郝 帅1, 2，徐立新1, 2

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300350；2. 高新船舶与深海开发装备协同创新中心，上海 200240)

针对浮体-张力筋腱非线性耦合系统，采用时域分析方法对局部系泊失效下的张力腿平台进行动力响应分析，重点研究两根筋腱失效时筋腱失效位置、波浪载荷参数与平台各自由度动力响应的关系．结果表明：局部系泊失效对平台横荡、纵荡、艏摇自由度的动力响应影响远小于横摇、纵摇、垂荡自由度；失效位置与平台动力响应关系密切，失效筋腱位置越集中，平台响应越大，反之亦然；筋腱失效后平台在不同波浪载荷参数下的运动特性及顶端张力表现各异．垂荡瞬态阶段响应对波高和波周期敏感性较强，垂荡稳态阶段响应对浪向、波高和波周期敏感性较强；纵摇(横摇)瞬态和稳态阶段响应对浪向、波高和波周期敏感性均较强；波浪载荷参数对筋腱顶端张力的影响较小．

浮体-张力筋腱耦合动动力学分析；局部系泊失效；失效位置；波浪载荷参数；动力响应；时域分析

张力腿平台(tension leg platform，TLP)是一种垂直系泊的半顺应性半刚性平台，是由刚性系统(平台上部结构、立柱与浮箱)和弹性系统(张力筋腱与立管)组成的复杂非线性动力耦合系统[1]．随着TLP作业水深的不断增加，筋腱载荷显著提高，结构系统运动的不稳定性增大，极端环境载荷易导致平台大幅升沉运动，甚至产生共振，这些都容易使筋腱张力超过结构承受极限，发生瞬态失效．同时，由于累积疲劳、腐蚀缺陷、意外碰撞等产生的局部结构损伤也可能会造成张力筋腱的失效，进而通过平台主体与张力筋腱的耦合作用影响整个系统的性能，最终导致平台倾覆、人员伤亡、环境污染等特大灾难性事故的发生．

为了准确预测TLP与其系泊系统的耦合动力响应，国内外学者开展了大量研究[2-5]，多数采用时域方法．Tahar等[6]根据非线性梁理论对系缆进行简化，开发出一种可以模拟浮体-系缆-立管系统非线性动力响应的时域耦合分析方法，并进行了截断模型实验验证.Ahmad等[7]和Siddiqui等[8]考虑了不同浸水、浮力和垂直方向波浪力引起的张力变化等各种非线性效应，对筋腱张力变化引起的次谐波共振以及浸水效果引起的次谐波共振进行了分析．Yang等[9-10]运用高阶边界元方法处理波浪与结构的关系，基于细长杆理论对系缆、立管进行简化，建立了深水浮式结构-系泊系统的耦合分析方法，并研究了各结构间的动力耦合效应．谷家扬[11]对多工况下TLP的运动耦合响应、张力筋腱和立管的张力特性进行了数值求解，并进行了模型实验验证(1∶40)．Jayalekshmi等[12]考虑了舱体-筋腱的耦合动态响应，针对一类单柱TLP开展实验研究，研究表明舱体-筋腱的耦合会产生显著的动力放大效应，从而进一步说明耦合分析在深水工程中的重要性．

深海作业环境异常复杂，TLP系统往往存在着发生各种失效的风险，学者们对于筋腱失效的瞬态响应也逐渐展开研究，Mansour等[13]分析了筋腱松弛、筋腱突然破裂以及移去单根筋腱后TLP在恶劣环境条件下的自存能力．Kim等[14]和Yang等[15]的研究主要是针对极端飓风载荷导致张力筋腱连接失效之后的平台系统瞬态响应特性，并初步分析了平台的生存性与完整性．Kim研究了筋腱在初始时刻失效和时域分析过程中失效对TLP瞬态响应的影响，并证明筋腱端部失效较底部脱落更加危险[15]．然而，对于筋腱失效位置、波浪载荷参数与筋腱失效后平台动力响应的规律性探究很少被提及．

针对传统TLP平台，在两根筋腱失效后剩余筋腱连续破坏的可能性激增，平台处于危险状态，且工业界要求两根筋腱失效后平台仍能保证自存，因此对两根筋腱失效后平台的动力响应研究有重要的现实意义．基于此，本文建立了浮体-筋腱非线性耦合模型，计及6个自由度之间的耦合作用，在规则波下模拟两根筋腱失效的时域响应全过程，对筋腱失效位置、组合形式与平台动力响应的关系进行了规律性探究；并分析了平台各阶段响应的运动特性(如响应幅值、平衡位置等)及筋腱顶端张力与入射波角度、波高和波周期参数的敏感性关系．

1 数值模型

1.1 几何模型

本研究选取一个典型的四立柱式张力腿平台“ISSC TLP”作为计算模型[16]，模型由浮体结构(立柱以及旁通)、张力腿筋腱以及海底基础装置构成，如图1所示．

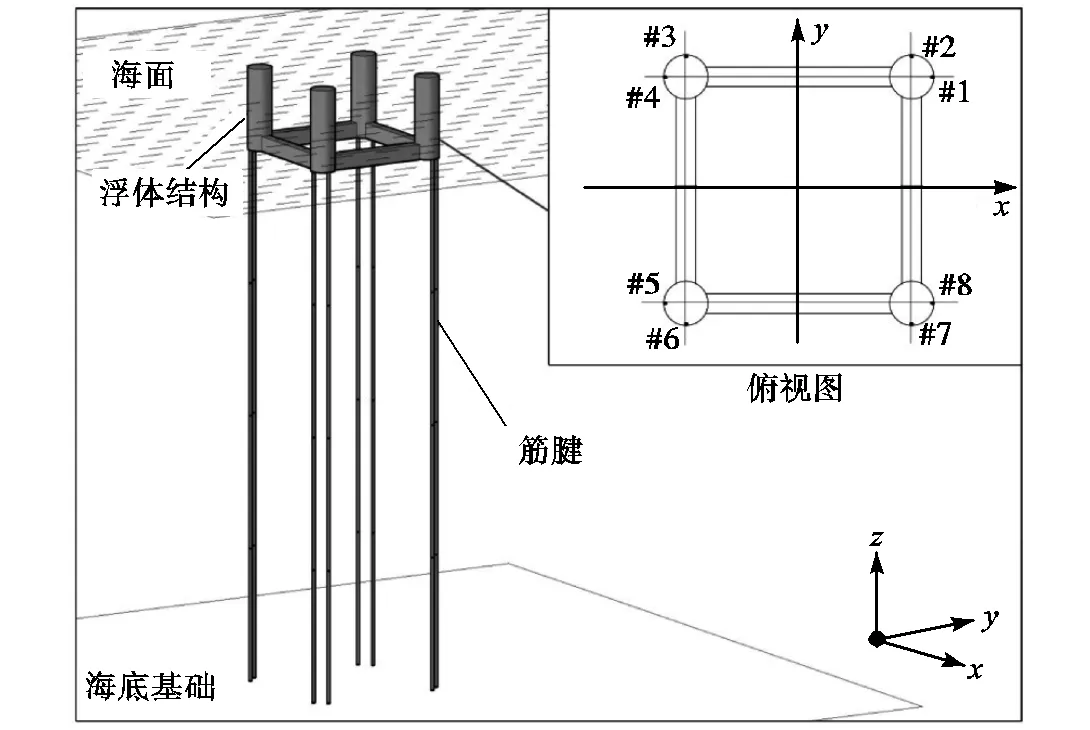
图1 张力腿平台浮体-筋腱布置

张力腿平台上部浮体结构以及张力筋腱的具体参数如表1所示．

表1 ISSCTLP主要参数

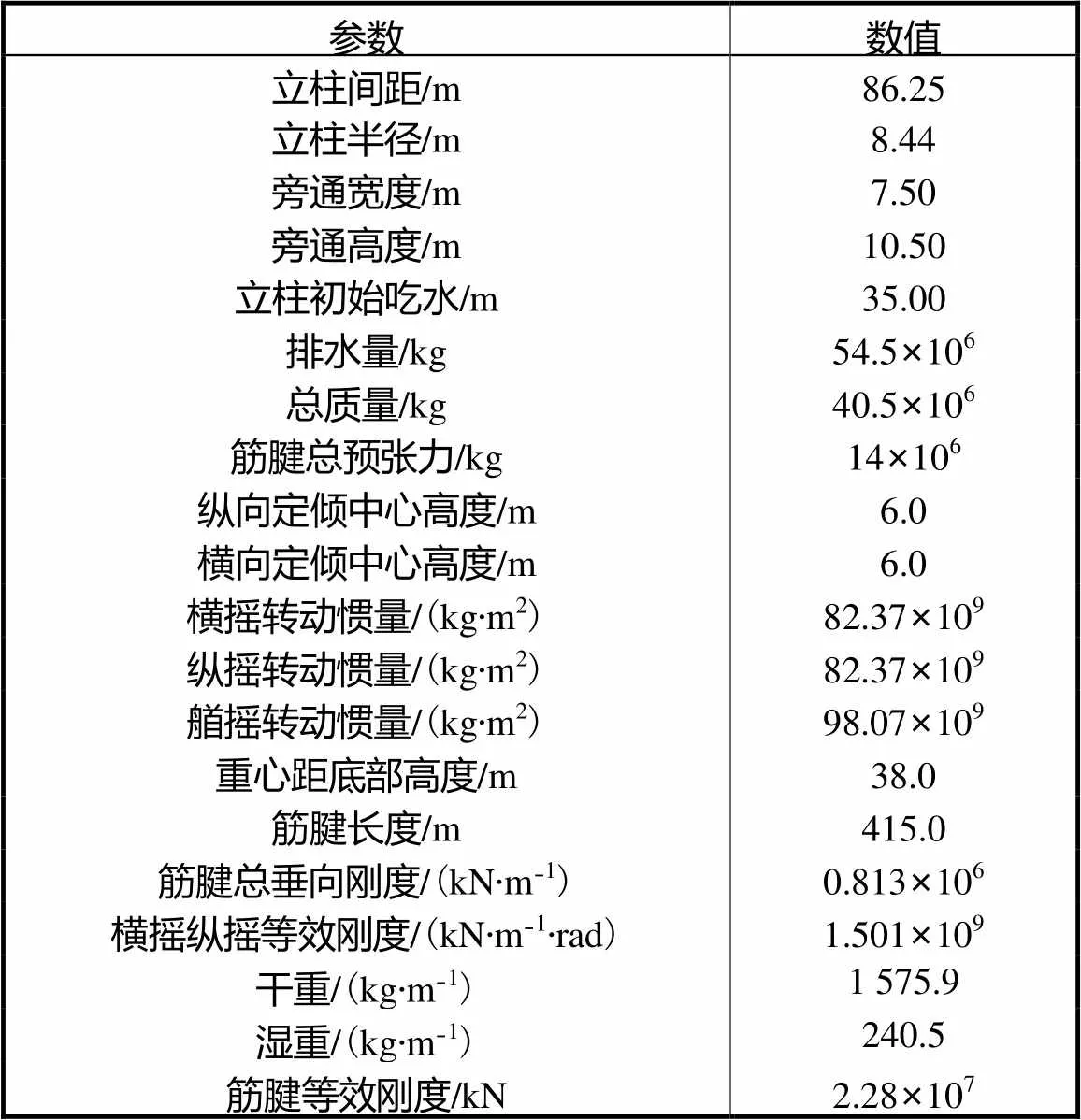
Tab.1 Parameters of ISSC TLP

1.2 网格划分

利用ANSYS®AQWATM软件进行有限元计算，对TLP浮体结构进行网格划分时，一个波浪长度至少覆盖5～8个最大尺寸单元[17]，划分网格时要根据需要计算的最大波浪频率设定网格的控制尺寸，网格越细，可计算的波浪载荷频率越大，同时对应着计算耗时的增加．本研究在保证精度的前提下选择效率最高的划分方式：整个浮体结构被划分为6,029个六面体单元，单元尺寸最大为5,m，最小为3,m．张力筋腱采用长径比较大的柔性圆柱形管模型进行模拟，使用tether单元，每根筋腱被划分为25个单元．

1.3 数值分析过程

数值分析过程如图2所示，首先，在几何模块中建立浮体和系泊系统的几何模型，浮体结构由面元模型和莫里森模型组成，筋腱用tether单元进行模拟；然后，通过接触模块设置结构之间的系泊属性，在水动力辐射模块进行频域计算，得到附加质量系数、附加阻尼系数、一阶波浪力以及传递函数等，为时域分析提供基础水动力数据；最后，在水动力响应模块中进行波浪载荷参数设置并完成局部筋腱失效后的时域计算．

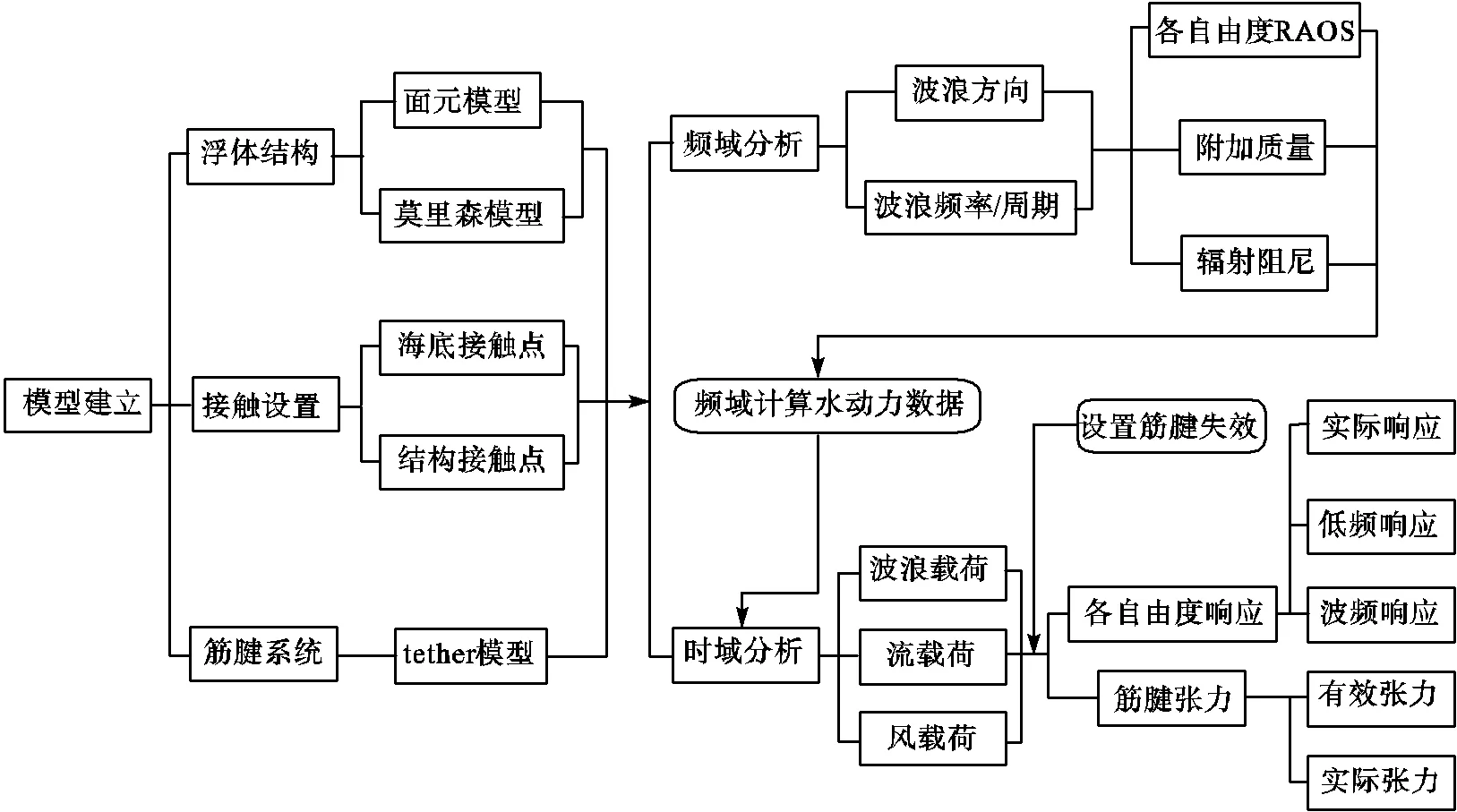
图2 数值分析流程

2 理论方法

2.1 三维势流理论

基于三维势流理论进行TLP水动力分析，假设TLP附近的流场理想，即无黏、无旋、有势，波浪场速度势是空间位置及时间的函数，其应满足如下边界 条件．

控制方程

线性化自由面条件

水底条件

物面条件

在直角坐标系中，沿波传播方向，沿静止水面法向；是水深参数；是物体的运动速度；是物面上的单位外法向矢量．

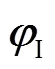
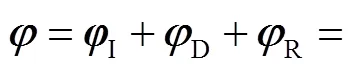
求出速度势之后，根据Bernoulli方程计算平台湿表面上的压力分布．

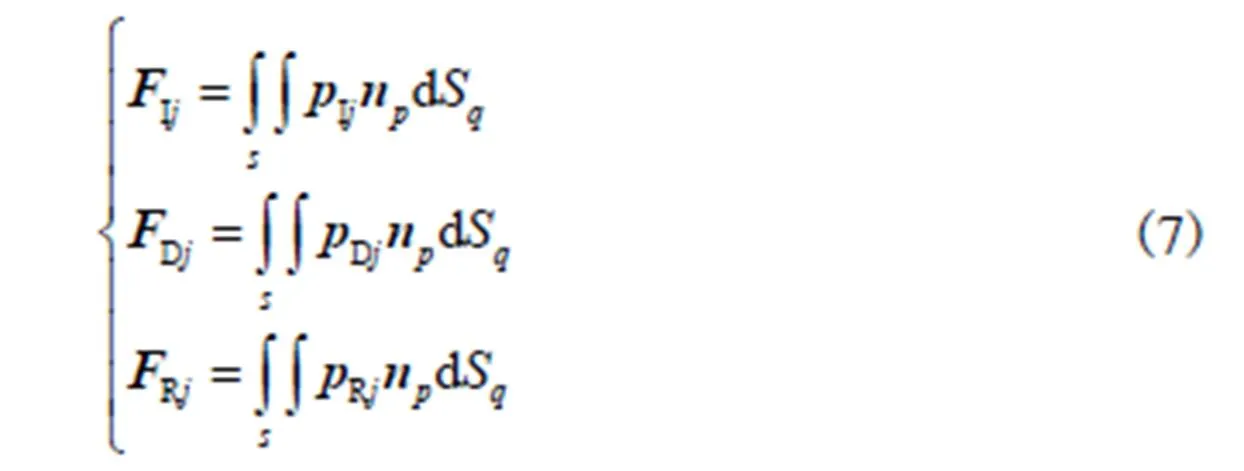
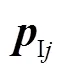
2.2 时域运动方程

在时域分析中，张力腿平台的运动方程为

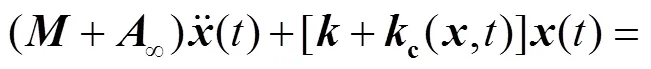
2.3 筋腱模型

本研究采用tether模型模拟实际作业中的TLP筋腱，每个单元受力包括3部分．

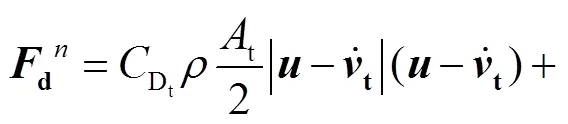
3 模型验证

本研究使用的张力腿平台模型来源于Gie和Boom的张力腿平台缩尺比实验[16]．包括英国海事技术有限公司、布朗根(英国)有限公司、英国伦敦大学学院等在内的17家组织机构对该TLP做过频域分析，计算得到的水动力参数与本文数值模拟得到的结果几乎相同．频域计算得到的水动力数据是时域计算的基础，因此充分证明了本次数值模拟的准确性．此前17家组织计算的水动力参数包括0°、22.5°、45°浪向下各自由度的RAO(幅值响应算子)、附加质量、辐射阻尼以及平均漂移力等[16]．因篇幅有限，选取部分对比数据如图3和图4所示．

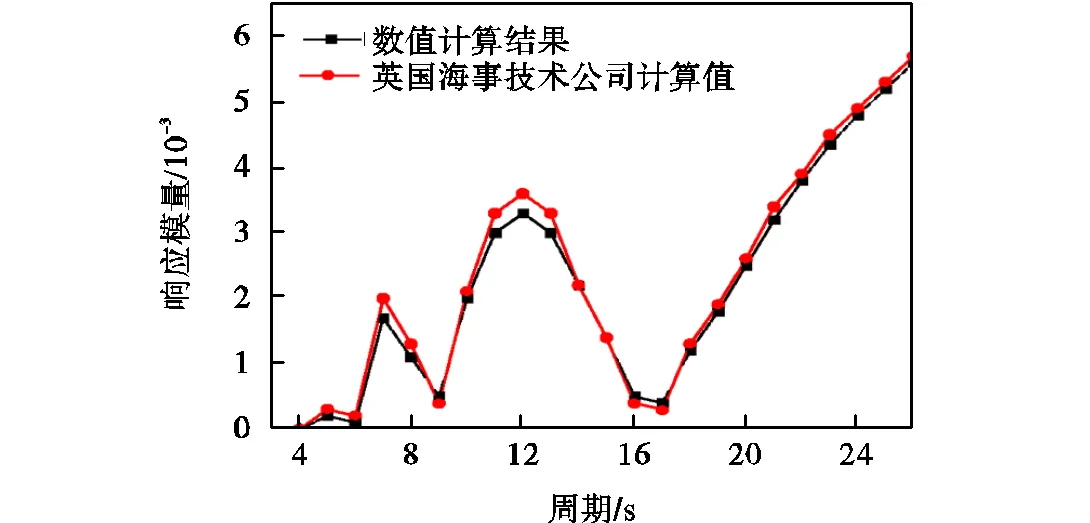
图3 22.5°浪向下垂荡响应模量

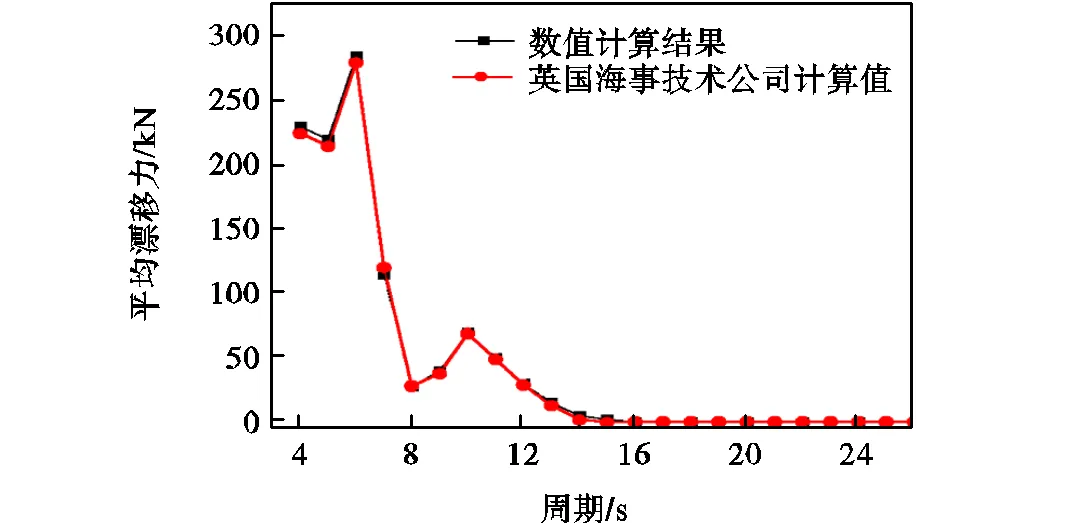
图4 0°浪向下纵荡平均漂移力

4 计算结果及讨论

4.1 不同数量筋腱失效后平台动力响应分析

平台筋腱位置编号及波浪方向如图5所示，定义波浪首先接触的位置为迎浪位置，反之为背浪位置．针对本典型张力腿平台，分别建立1根、2根、3根筋腱失效模型，在规则波下进行时域计算分析，取规则波波高6,m、周期10,s、浪向0°，设置筋腱在297.2,s同时失效(筋腱张力达到最大时)，以垂荡响应为例，对3种失效工况进行对比分析，如图6所示.

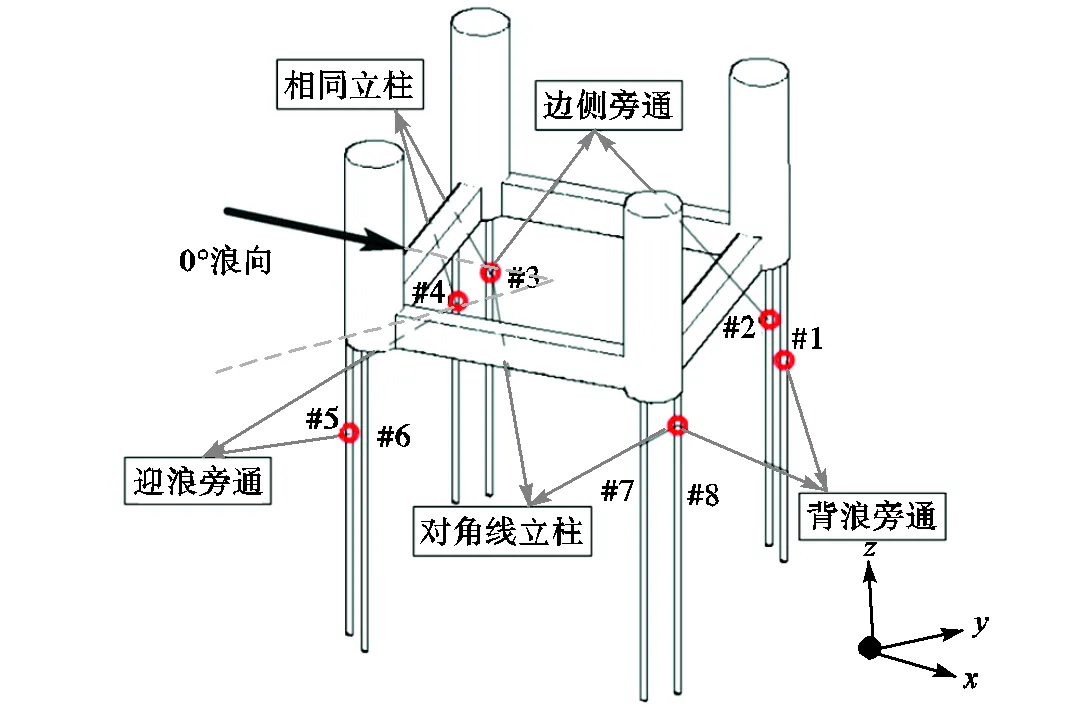
图5 0°浪向下筋腱失效位置示意

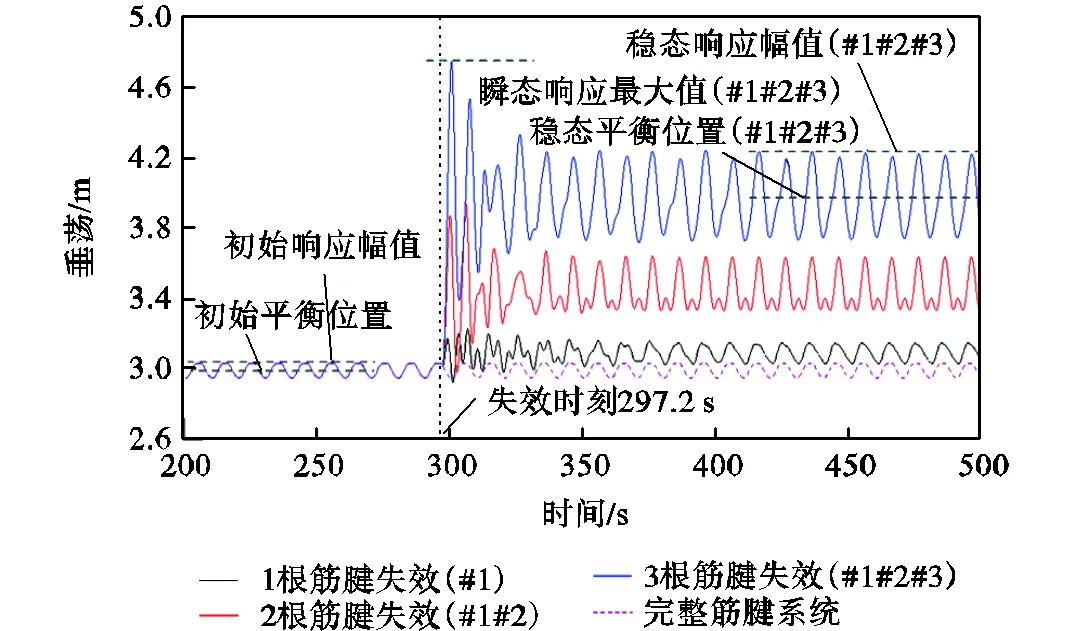
图6 不同数量筋腱失效后平台垂荡时历曲线

当1根筋腱失效后，平台瞬态响应最大值为3.22,m，较初始响应幅值仅增大了5.57%,．在整个时域响应过程中，剩余筋腱张力值均远小于极限张力值，故不会发生连续失效，平台仍处于安全状态．当2根筋腱失效后，系统垂荡自由度刚度严重缺失，平台产生了较大的瞬态响应，响应最大值较初始幅值增大了30.2%,；瞬态响应之后的稳态平衡位置和响应幅值都有明显提高，靠近失效位置的筋腱张力激增，接近其极限破断张力，平台处于临界危险状态．当3根筋腱失效后，平台垂荡自由度产生剧烈响应，瞬态响应幅值较初始幅值增大了56.4%,，且紧邻失效位置的#4筋腱顶端张力在筋腱失效瞬间激增，远超过极限张力值，将会引发连续失效，平台终将失去自存能力．综上所述，1根筋腱失效后平台处于较安全状态，2根筋腱失效后平台处于临界危险状态，3根筋腱失效后平台将连续破坏直至倾覆．通常工业界要求平台设计时需具备2根筋腱失效之后TLP仍能自存的能力，因此本文重点讨论临近危险状态即2根筋腱失效后平台的动力响应特征．

4.2 筋腱失效位置与平台动力响应的关系

由于长期作业，实际在位的TLP某些筋腱处于疲劳损伤状态，储备张力值远低于设计张力．在极端环境载荷下，筋腱失效会导致剩余筋腱张力水平在短时间内迅速增加，诱发连续失效．当2根筋腱连续失效的过程极其短暂时，可以认为失效同时发生，这具有很大的危险性．本节将不同位置的2根筋腱组合，对TLP进行局部失效后的时域分析，研究筋腱失效位置与张力腿平台各自由度动力响应的关系．6组不同位置的失效组合具体工况分类见表2．

表2 筋腱失效组合位置

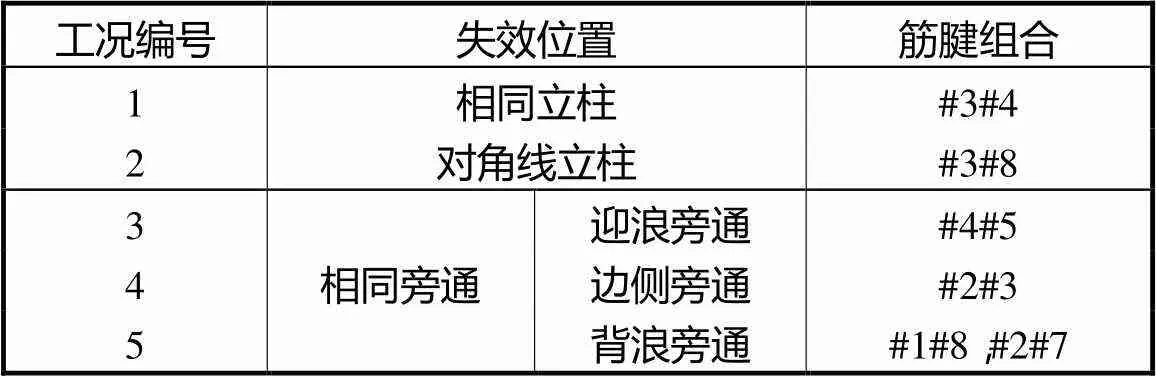
Tab.2 Classification of tendon failure position

4.2.1 规则波下局部筋腱失效后平台动力响应分析

张力腿平台在平面内的运动响应(纵荡、横荡和艏摇)具有柔性特点，即顺应性．由于TLP结构的对称性，局部筋腱失效后，平台横荡和纵荡瞬态响应规律一致，只需考虑其一即可．

计算选取规则波波高为8,m、周期为12,s，经试算选择时域时长1,000,s，计算步长0.1,s，筋腱失效时刻为295,s(筋腱张力达到最大时)．图7是部分筋腱组合失效后TLP横荡自由度的时历响应曲线，将各种工况下的最大响应值变化量统计如表3所示．

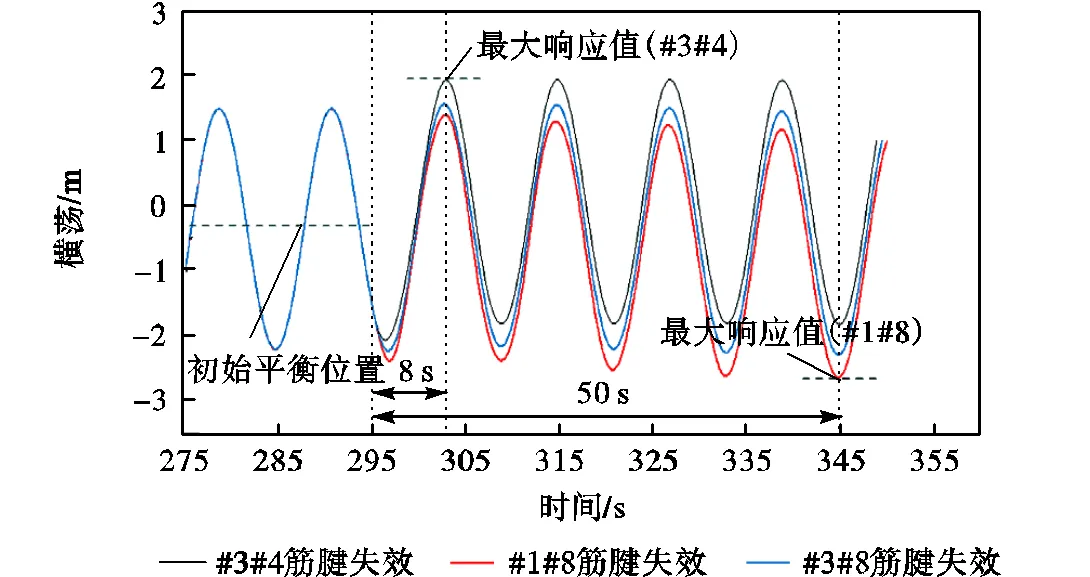
图7 局部系泊失效过程TLP横荡时历曲线

由表3可知，筋腱失效后TLP横荡响应最大值较初始响应幅值的最大偏移量为0.5,m(工况1)，仅占作业水深的0.11%,．结合横荡自由度顺应性特征，该瞬态效应引起的位移变化可以忽略不计．值得注意的是，#3#4筋腱失效后，TLP横荡最大响应出现在303,s，距离失效时刻仅8,s；但#1#8筋腱失效后，TLP横荡最大响应并没有在失效瞬间发生，而是出现在距离失效时刻约50,s的时间节点处．因此对于横荡自由度，TLP在局部失效后的瞬态响应不明显，且部分失效组合引起的瞬态效果在时间上具有一定滞后性.

表3 横荡和艏摇响应统计值

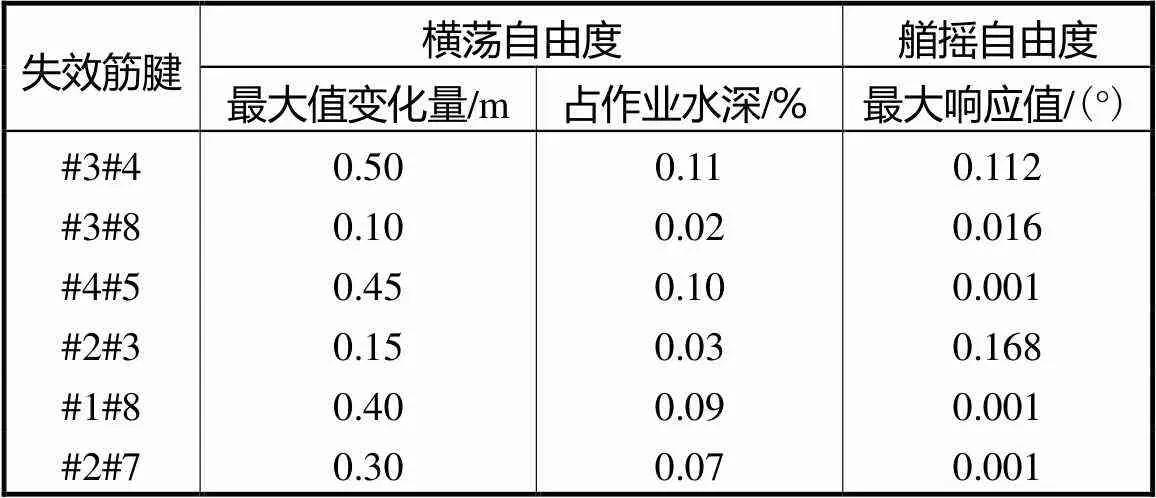
Tab.3 Statistics of sway and yaw responses

图8是部分筋腱组合失效后TLP艏摇时历响应曲线，各种失效工况下的艏摇最大响应值见表3．对比各失效工况下的艏摇响应，发现#3#4、#2#3筋腱组合失效后TLP艏摇响应发生激增，响应值远大于其他失效组合．原因为当上述筋腱组合失效后，在筋腱失效位置、波浪作用方向等一系列非对称因素作用下，平台在横荡和纵荡自由度产生了非对称响应，而艏摇与纵荡、横荡有明显的耦合效应，间接导致艏摇响应产生跨量级的激增．与横荡自由度类似，#3#4筋腱失效后，艏摇响应最大值出现在350,s左右，说明部分失效组合引起的瞬态效果具有一定滞后性．

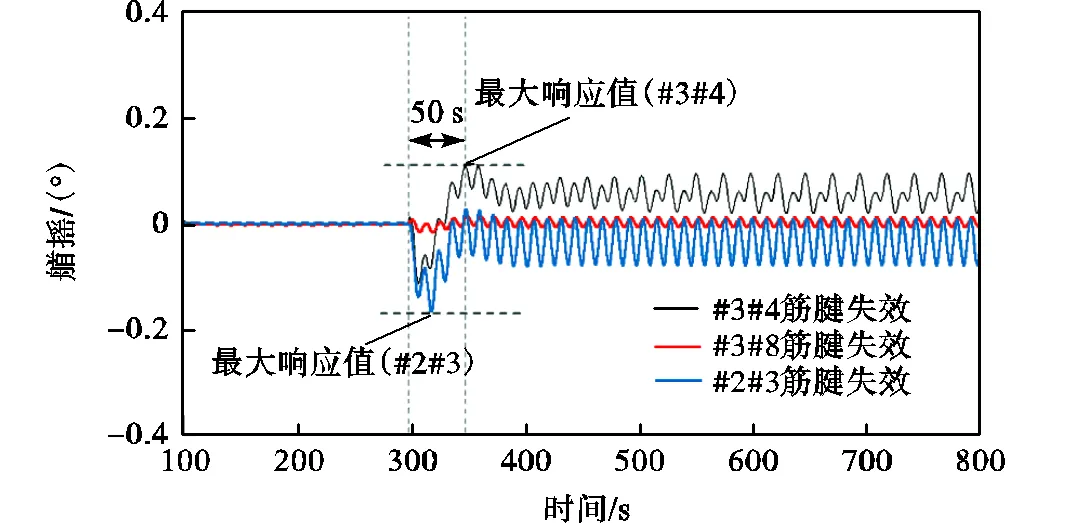
图8 局部系泊失效过程TLP艏摇时历曲线

张力腿平台的筋腱系统往往在预张力作用下时刻处于张紧状态，巨大的张力使平台竖直面上运动响应较小，几乎近似于刚性．因为筋腱为刚性自由度提供了直接约束，所以筋腱失效会直接影响横摇、纵摇和垂荡的动力响应，这将是本文的研究重点．

图9、图10是在0°浪向规则波下不同筋腱组合失效后TLP垂荡、纵摇响应时历曲线．

现将时域响应过程进行划分，以#3#4筋腱失效后垂荡响应为例：0～295,s为筋腱系统完好的初始响应阶段；295～315,s为筋腱失效后的瞬态响应阶段，在此期间响应发生较大波动；315,s以后为稳态响应阶段，响应趋于稳定平衡．通过研究对比不同响应阶段的运动特性(如响应幅值、平衡位置等)来更全面地分析响应规律．

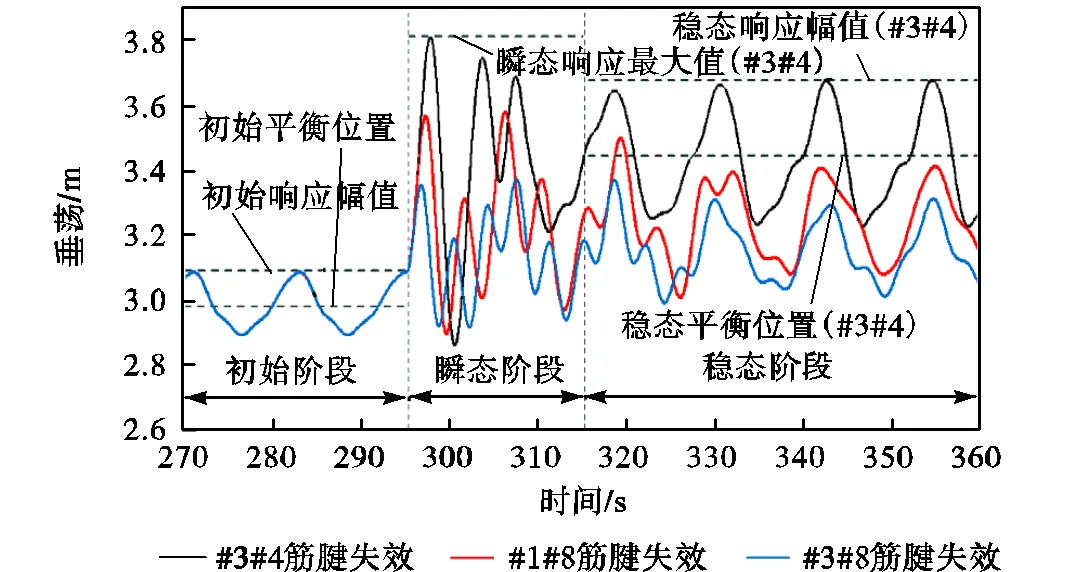
图9 局部系泊失效过程TLP垂荡时历曲线

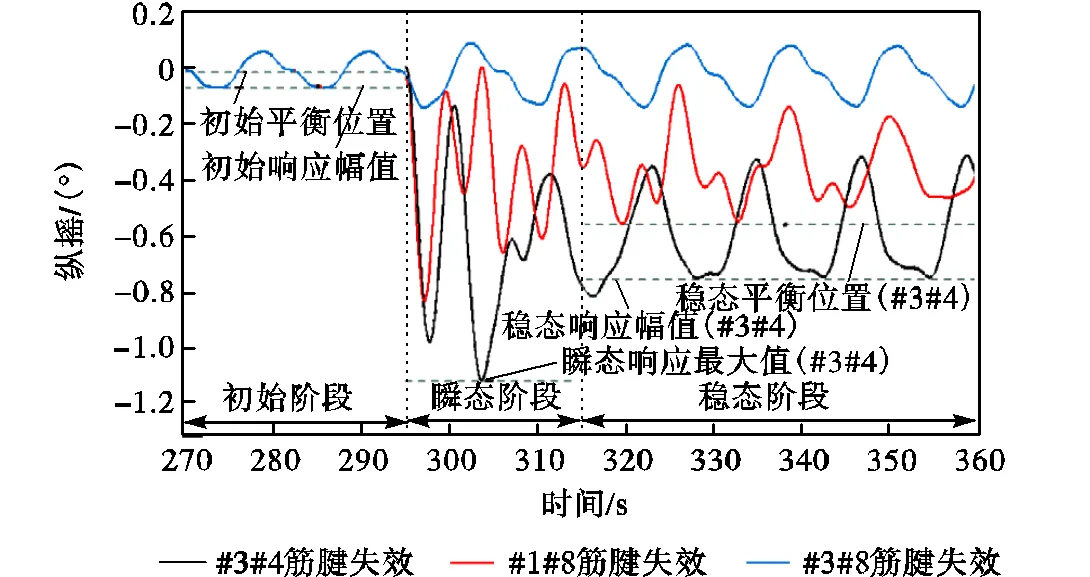
图10 局部系泊失效过程TLP纵摇时历曲线

为了清晰全面地表现出局部筋腱失效后平台动力响应大小，设置如下无量纲参数：

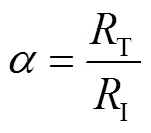
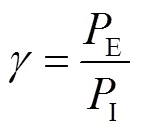
就垂荡和纵摇自由度而言，同一立柱下的2根筋腱失效响应参数最大，同一旁通上的2根筋腱失效响应参数次之，对角线立柱下的筋腱失效响应参数最小．原因为当不同筋腱组合失效后平台垂荡刚度相近，但纵摇刚度差别迥异，其中同一立柱下筋腱组合失效使平台一角约束缺失，纵摇刚度产生严重折减，因此在波浪载荷作用下平台产生较强的纵摇响应．垂荡与纵摇有强耦合作用，所以也表现出明显的动力响应，使TLP处于最危险状态．

表4 垂荡和纵摇响应参数统计

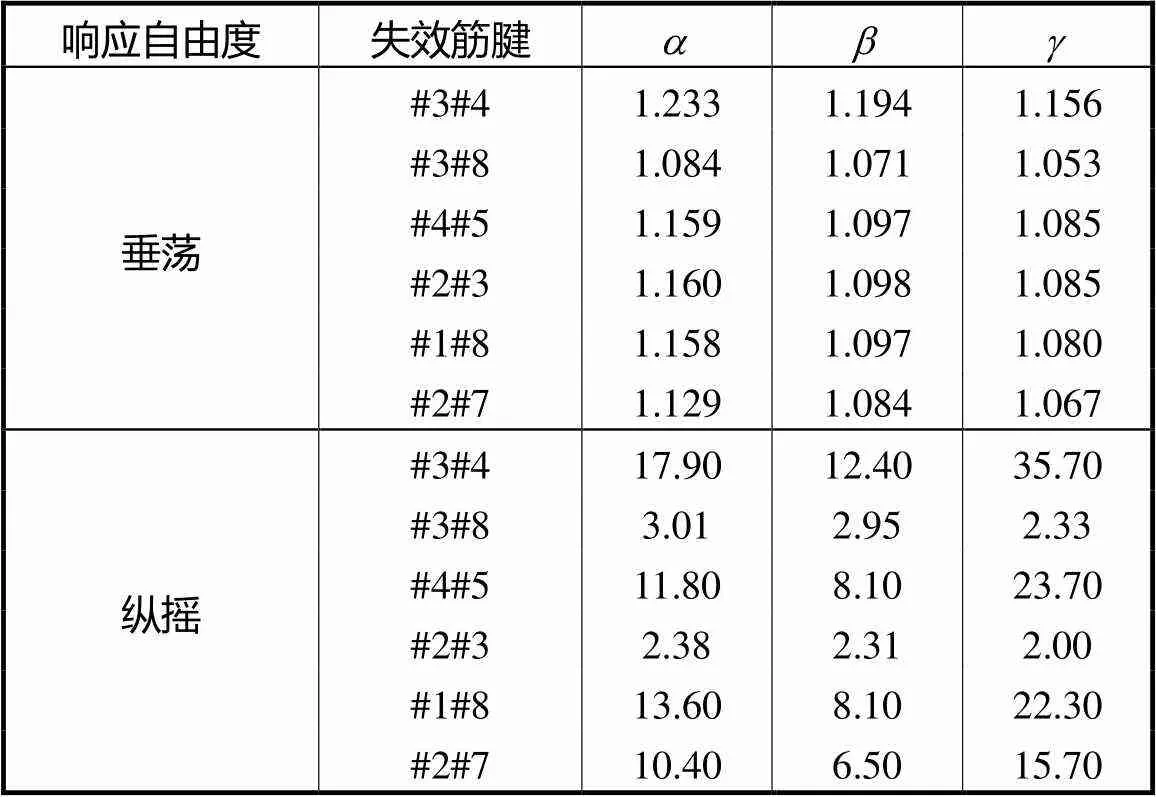
Tab.4 Parameters of heave and pitch responses

#1#8失效工况的垂荡响应参数均大于#2#7失效工况，说明同一旁通的外侧筋腱较内侧筋腱对TLP垂荡响应的影响更大．原因为#1#8筋腱失效之后，TLP会绕着次转轴(次转轴平行且更靠近迎浪旁通)转动，#2#7筋腱失效亦然，但#2#7筋腱到次转轴的距离较#1#8筋腱更近，所以局部失效之后，#2#7筋腱张力水平高于#1#8筋腱．基于小变形前提，考虑筋腱的轴向刚度相同，#2#7筋腱的伸长量大于#1#8筋腱，也就是说#1#8筋腱组合失效引起的垂荡响应幅值大于#2#7筋腱组合失效．

#1#8失效后的响应参数和#4#5失效后的响应参数相差均在0.03%,之内，说明失效筋腱所处迎浪位置和背浪位置对TLP垂荡响应影响不大．

由于垂荡和纵摇、横摇的耦合关系，筋腱失效位置和TLP纵摇响应参数变化规律与垂荡相似，但存在特殊情况，从表4可知#2#3失效后纵摇响应参数很小，因为#2#3筋腱失效后暂存筋腱组成的系泊系统仍关于轴对称，结构对称性未被破坏，整个系统纵摇刚度较大，所以TLP纵摇响应不明显．因此，同一旁通下筋腱失效，若筋腱失效位置关于纵(横)荡自由度对称，则TLP纵(横)摇响应很小．

4.2.2 不规则波下局部筋腱失效后平台的动力响应分析

考虑中国南海百年一遇的海况(表5)，设置系泊系统两根筋腱在为清晰量化平台响应大小，综合对比不同阶段运动特性参数：瞬态响应最大值，稳态响应幅值以及稳态平衡位置．由图11(a)可知，#3#4筋腱(相同立柱)失效后，垂荡响应参数最大，其中瞬态响应最大值较初始响应幅值增大了27%,，TLP处于最危险状态；#4#5筋腱(相同旁通)失效后，垂荡响应居中；#1#6筋腱(对角线立柱)失效后，垂荡响应最小．由图11(b)可知，在不规则波下，#1#8筋腱失效后的垂荡响应参数均大于#2#7筋腱失效，可知在不规则波作用下外侧筋腱较内侧筋腱对TLP垂荡影响更大．

表5 中国南海百年一遇海况参数

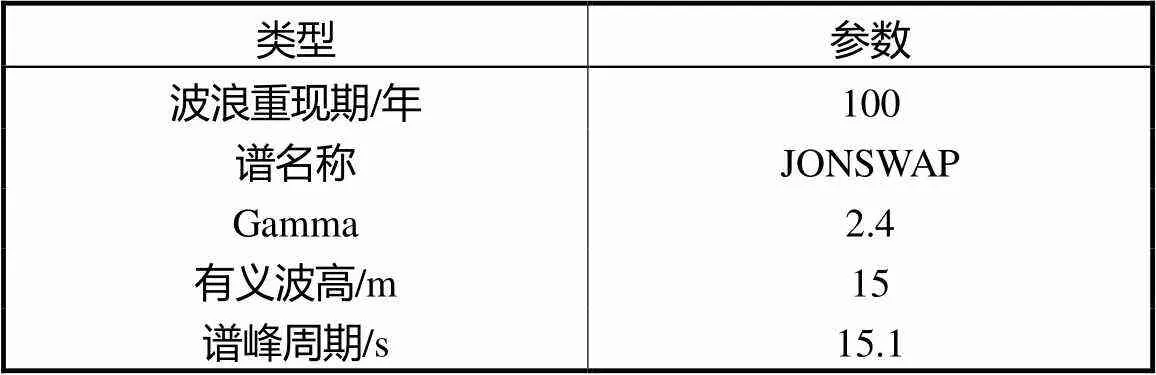
Tab.5 Parameters of 100-year sea conditions in South China Sea

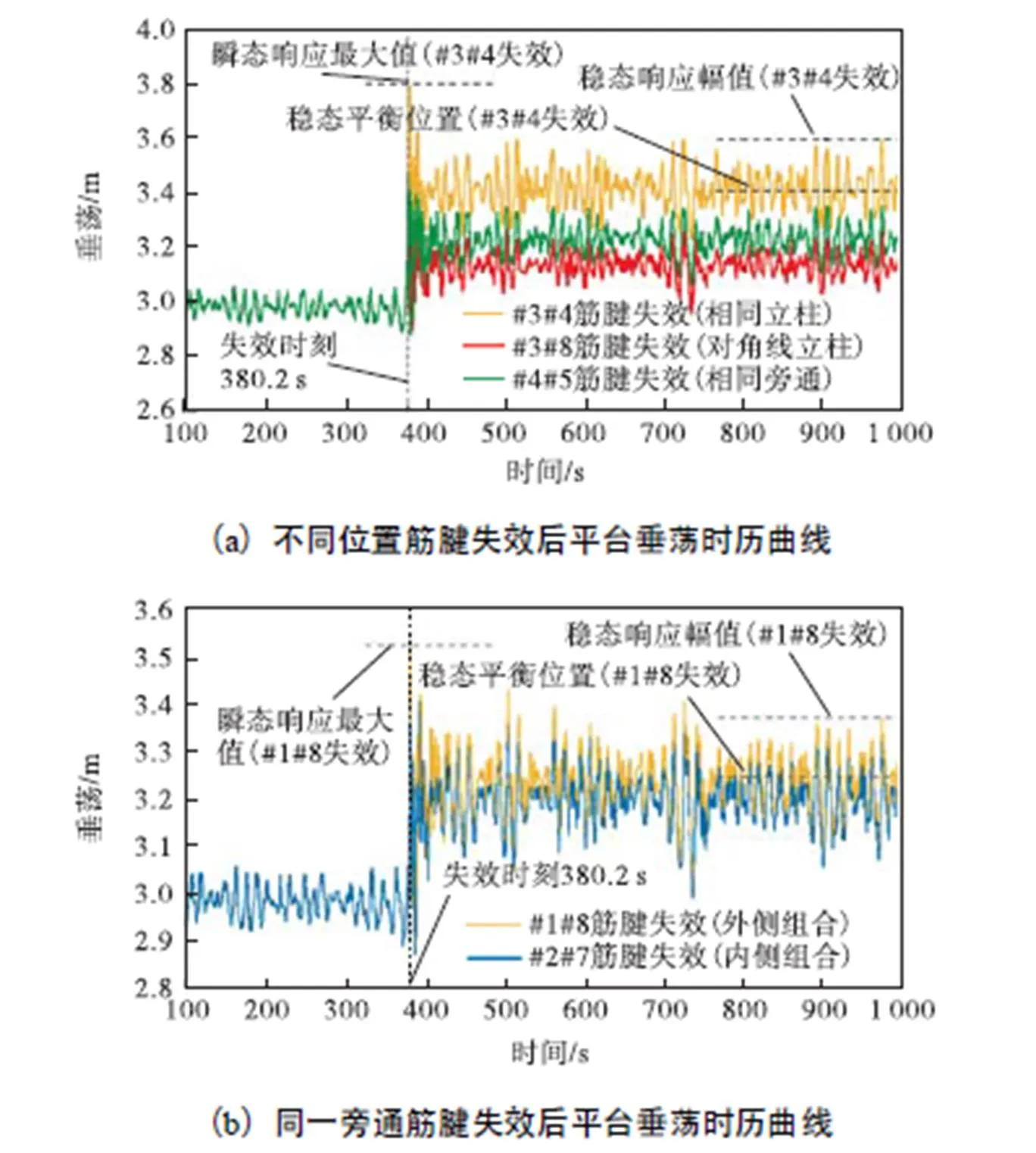
图11不规则波下局部筋腱失效后TLP垂荡时历曲线

由于垂荡和纵摇的耦合作用，局部失效后平台纵摇响应规律与垂荡类似．由图12(a)可知，对于纵摇，#3#4筋腱失效后，TLP纵摇响应最大；#4#5筋腱失效后，纵摇响应居中；#1#6筋腱失效后，TLP纵摇响应与完整筋腱系统响应相差无几，影响较小．由图12(b)可知，#1#8筋腱失效后，纵摇响应大于#2#7筋腱失效；#2#3筋腱失效后，平台纵摇响应很小，因为失效后平台纵摇刚度较大，响应不明显．

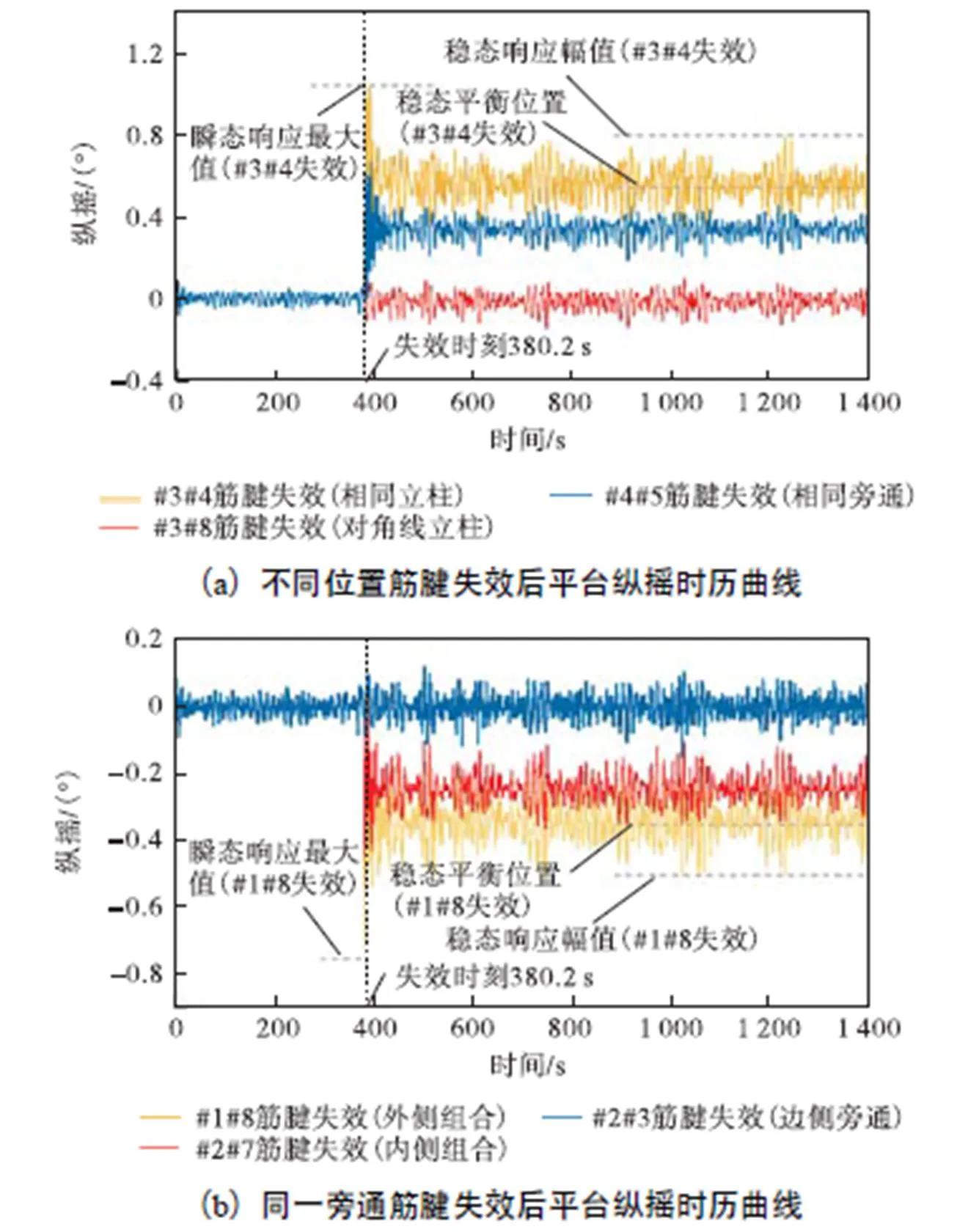
图12 不规则波下局部筋腱失效后TLP纵摇时历曲线

综上对比可知，规则波下得到的筋腱失效位置与TLP平台垂荡和纵摇(横摇)的瞬态响应规律在不规则波作用下同样适用．

4.3 波浪载荷参数与筋腱失效后平台动力响应关系

通过研究筋腱失效位置与平台动力响应的关系，发现筋腱失效后平台横荡、纵荡、艏摇自由度的瞬态响应效果远小于垂荡、横摇、纵摇自由度，因此，在研究波浪载荷参数与筋腱失效后平台动力响应的关系时，重点考虑垂荡、横摇和纵摇自由度，并将其作为主控自由度．

计算工况由不同波高(＝6,m，8,m，10,m)、不同波周期(＝10,s，12,s，14,s)及不同入射波角度 (＝0°，10°，20°)组合而成，如A0H6T10表示入射波角度0°、波高6,m、波周期10,s的波浪载荷；筋腱失效组合选择最危险的失效模式，相同立柱下的两根筋腱同时失效．本文对不同入射波角度、波高和波周期展开讨论．

4.3.1 不同浪向对筋腱失效后平台动力响应的影响

选取规则波的波高为6,m，波周期为10,s，入射角度分别取0°、10°、20°；设置#1#2筋腱在297.2,s失效．

因为张力腿平台结构的对称性，平台横摇和纵摇响应有相似的变化规律，所以只需分析固定浪向下主控自由度的响应规律即可．在不同浪向下，对局部失效后平台进行时域响应求解，并通过快速傅里叶变换(FFT)对稳态响应阶段进行频谱分析，平台垂荡和纵摇的动力响应结果如图13和图14所示．

根据局部系泊失效后平台时域响应过程的划分，重点对比不同响应阶段的运动参数：瞬态响应阶段的最大值、稳态响应阶段的幅值以及平衡位置．

图13的计算结果表明：在筋腱完好的初始阶段，不同浪向下平台的垂荡响应幅值和平衡位置几乎相同．局部筋腱失效后，在瞬态响应阶段，平台运动最大值相同，均为3.92,m；在稳态响应阶段，随着浪向的增大，平台的响应幅值逐渐增大，最大相差约75.1%,；平台在稳态响应阶段的平衡位置保持不变；通过快速傅里叶变换对稳态响应阶段进行频谱分析，发现存在较强的2倍频成分以及微弱的3倍、4倍频成分，局部系泊失效后TLP运动稳定性下降．随着入射波角度的增加，2倍频分量幅值增长明显．综上可知，浪向对局部筋腱失效后平台稳态阶段响应有影响，对瞬态阶段响应影响较小．

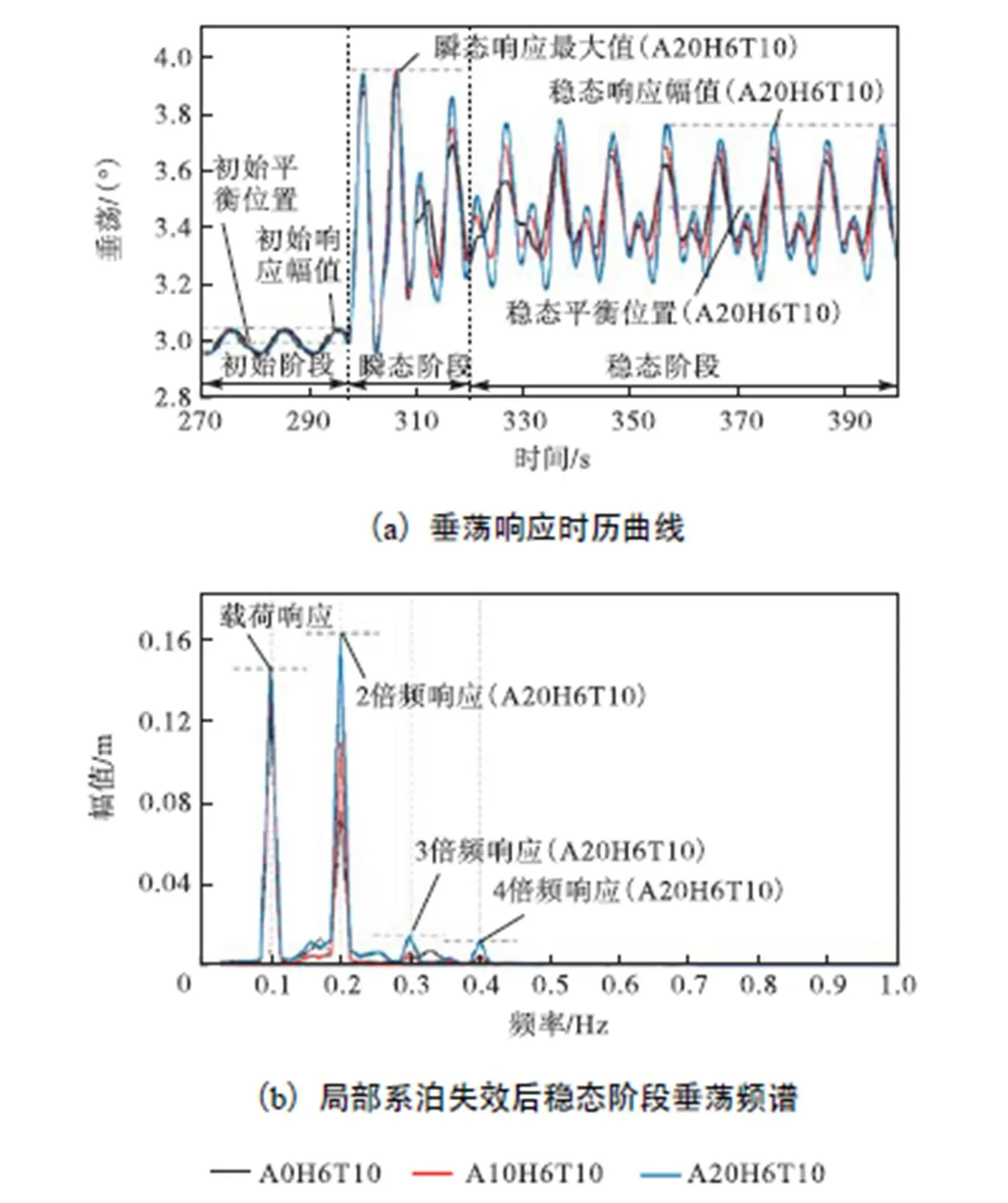
图13 不同浪向下筋腱失效过程TLP垂荡动力响应

从图14可知，筋腱未失效时，入射波角对纵摇的影响甚微．局部筋腱失效后，随着入射波角度的增大，瞬态响应阶段最大响应值逐渐增大；在稳态响应阶段中外激励频率分量随着入射角度增加而不断增加，幅值最大相差87.7%,．虽出现一定量的二倍频成分，但其与入射波角度相关性较小．因此，局部失效后平台纵摇各阶段响应对浪向参数的敏感度较强，且与垂荡响应变化规律又不尽相同．

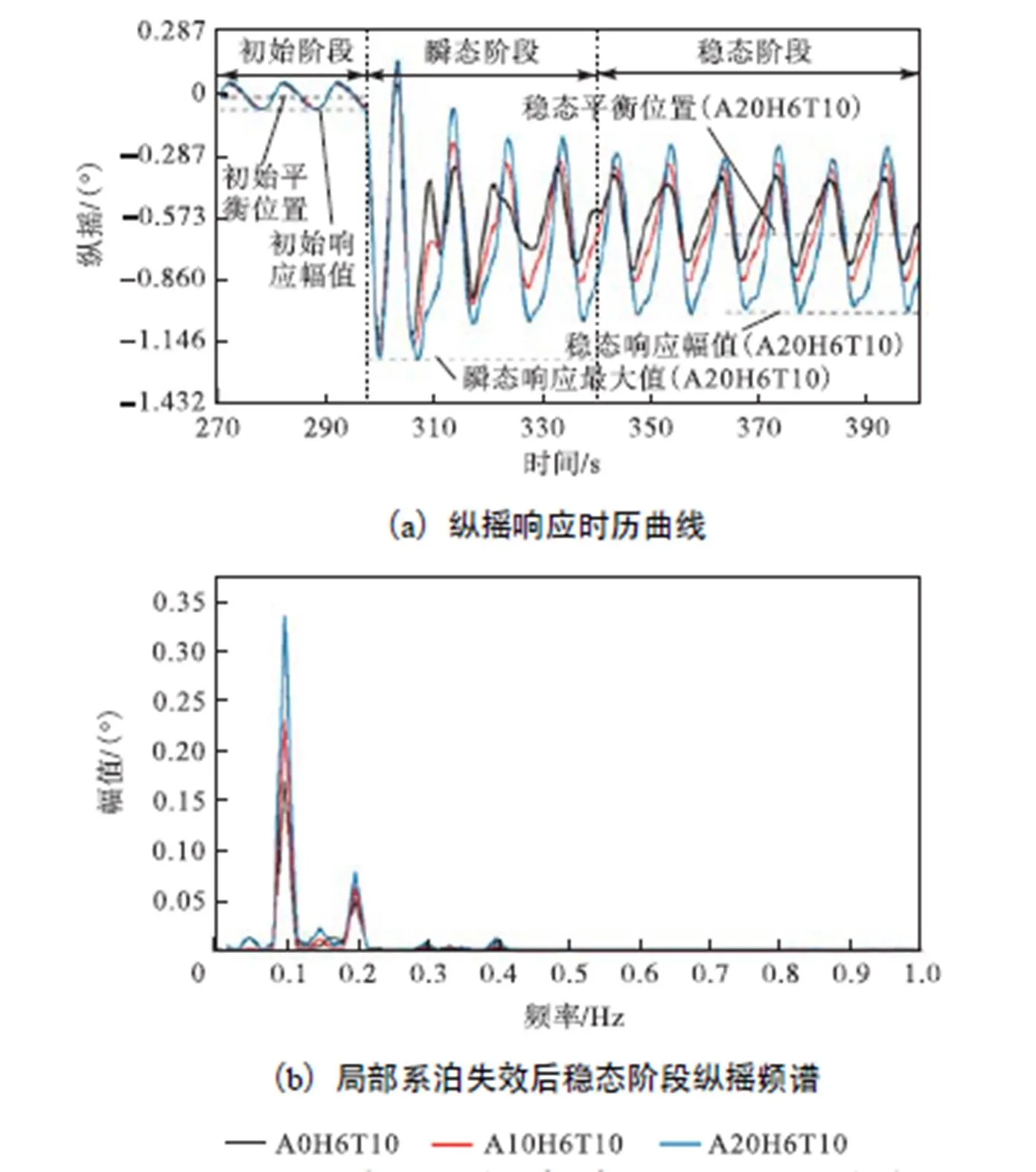
图14 不同浪向下筋腱失效过程TLP纵摇动力响应

因为TLP系泊系统为垂荡、纵(横)摇自由度提供较强的刚性约束，所以当局部筋腱失效后，垂荡和纵(横)摇自由度刚度较初始刚度均大幅减小．当浪向改变时，波浪力沿垂向分量变化不大，所以垂荡响应对浪向参数敏感性较弱；而波浪力的水平分量随着浪向的改变而产生明显改变，所以纵摇响应对浪向表现出较强的敏感性．

4.3.2 不同波高对筋腱失效后平台动力响应的影响

选取规则波的浪向为0°，波周期为10,s，波高分别取6,m、8,m、10,m．在0°浪向下，垂荡与纵摇是主控摇动自由度．不同波高下，平台在局部系泊失效后垂荡和纵摇动力响应结果如图15和图16所示．

从图15可知，在筋腱完好的初始阶段，随着波高的增大，垂荡幅值逐渐增大，垂荡平衡位置逐渐减小．局部筋腱失效后，在瞬态响应阶段，随着波高的增大，运动最大值逐渐增大．在稳态响应阶段出现的2倍频成分较明显，外激励频率分量与2倍频分量随着波高提升，均不断增长，稳态响应幅值最大相差93.3%,．稳态平衡位置保持不变，且存在一定的相位差，这是由于不同波高产生不同垂向分力造成的．波高越大，稳态阶段响应幅值较初始阶段幅值的增加量越大，这是由于系泊系统破坏使得垂向约束减小所致．因此，局部筋腱失效后垂荡各阶段响应对波高敏感度均较强．

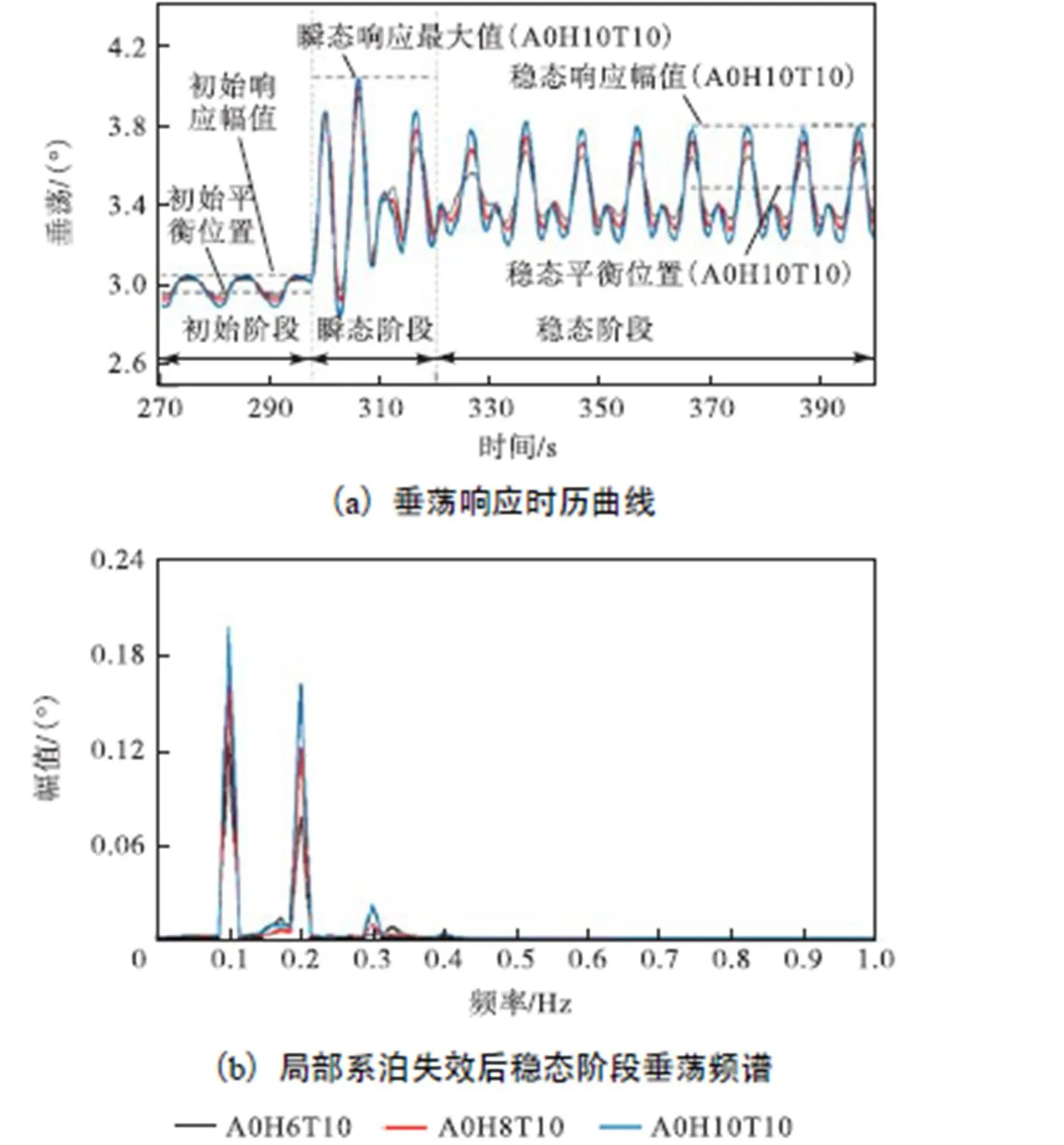
图15 不同波高下筋腱失效过程TLP垂荡动力响应

如图16所示，在初始阶段，不同波高下的纵摇平衡位置几乎不变，但响应幅值随着波高增大而增大．在局部筋腱失效之后，随着波高的增大，瞬态响应最大值增大．稳态响应幅值增大，最多相差72.7%,，但平衡位置几乎不变．与垂荡响应类似，稳态响应也出现较强的2倍频成分，且外载荷频率分量与2倍频分量均与波高有一定的相关性．由于纵摇和垂荡自由度的强耦合性，波高对局部失效后平台各阶段纵摇响应的影响与垂荡相似，但敏感性比垂荡稍微弱一些．

出现上述规律原因为局部系泊失效会使平台各自由度的刚度有不同程度的折损．针对本次研究的典型TLP模型，当#1#2筋腱失效后，平台垂荡自由度的刚度较初始刚度减小比重大于纵摇自由度，即平台垂荡自由度的回复能力损失较纵摇更严重，导致平台垂荡响应更剧烈，因此垂荡对波高参数的敏感性略强于纵摇．

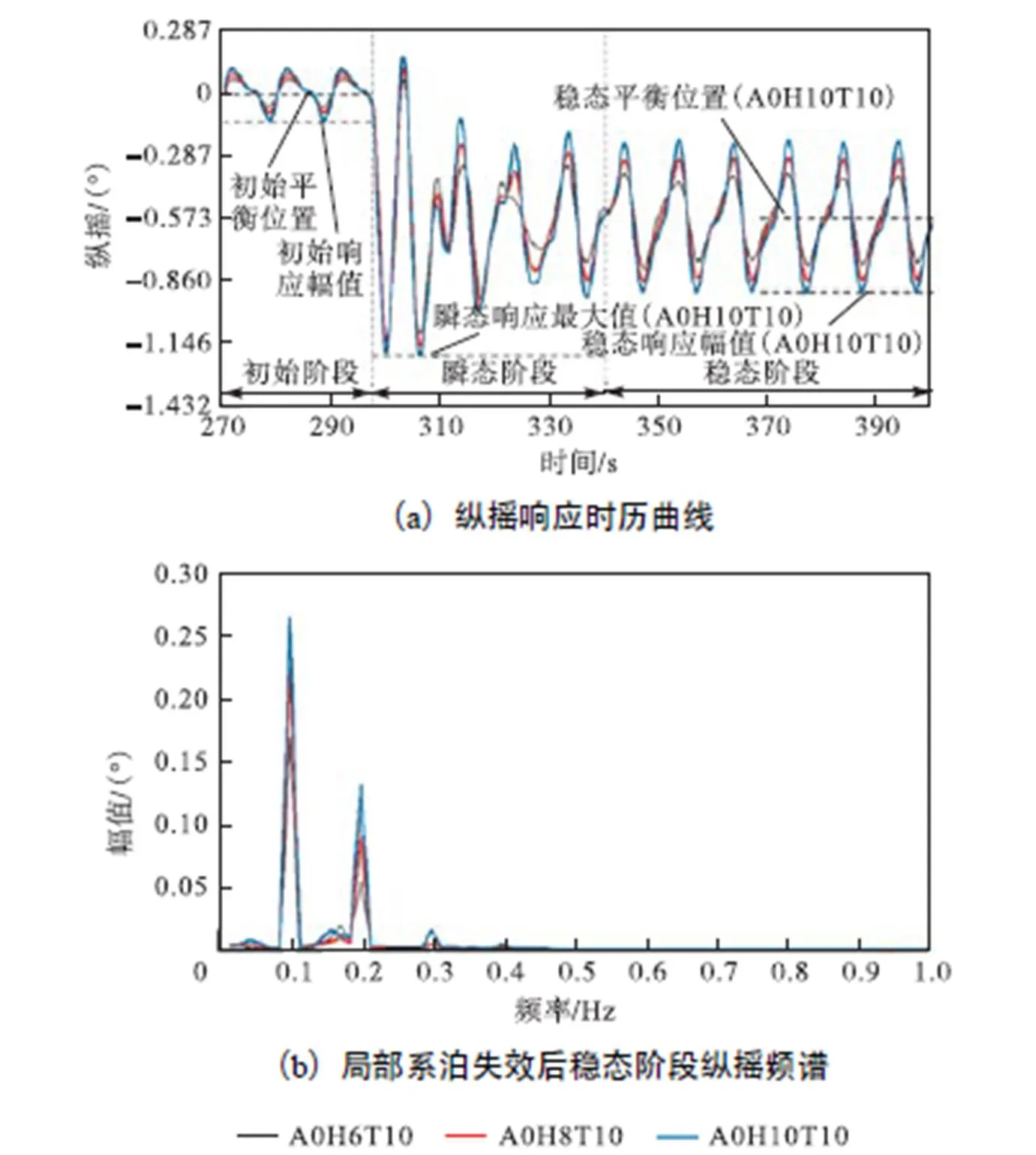
图16 不同波高下筋腱失效过程TLP纵摇动力响应

4.3.3 不同波浪周期对筋腱失效后平台动力响应的影响

选取规则波的浪向为0°，波高为6,m，波浪周期分别取10,s、12,s、14,s．不同波浪周期下，平台在局部筋腱失效后垂荡和纵摇动力响应结果如图17和图18所示．

不同波浪周期下，在初始阶段平台垂荡与纵摇的变化极为相似：时历曲线都存在相位差；平衡位置都基本不变．如图17所示，局部筋腱失效后，随着波浪周期的增大，瞬态阶段垂荡响应最大值越来越小．进入稳态阶段，垂荡平衡位置几乎保持不变，稳态幅值最大相差114.3%,，且与波浪周期并不是线性递变，3种工况中周期为12,s的波浪载荷对应的响应幅值最大，平台响应出现了较强的2倍频成分，周期为10,s载荷的影响次之，周期为14,s载荷的影响最小．与完整平台的在不同波周期下的运动幅值变化(如图3)相比，周期为10,s的波浪载荷下运动幅值上升明显．原因为：完整筋腱系统下平台的垂荡固有周期约为3.4,s，两根筋腱失效后，垂荡自由度的刚度减小，对与其周期接近的波浪载荷会产生一定的动力放大效果．综上所述，局部筋腱失效后平台垂荡各阶段响应对波浪周期的敏感度较强，且接近失效系统垂荡固有周期的波浪载荷在稳态阶段更容易产生较大的响应幅值．

就纵摇自由度而言，筋腱失效后，随着波浪周期增大，纵摇瞬态响应最大值减小，最大相差20.3%,；不同波浪周期的稳态响应幅值不同，最大相差79.3%,，平衡位置相差无几；在频谱分析中，不同波浪周期载荷参数下平台纵摇运动均出现了不同程度的二倍频成分，其规律与垂荡基本一致．因此，波浪周期对局部失效后纵摇各阶段响应也有较大的影响．

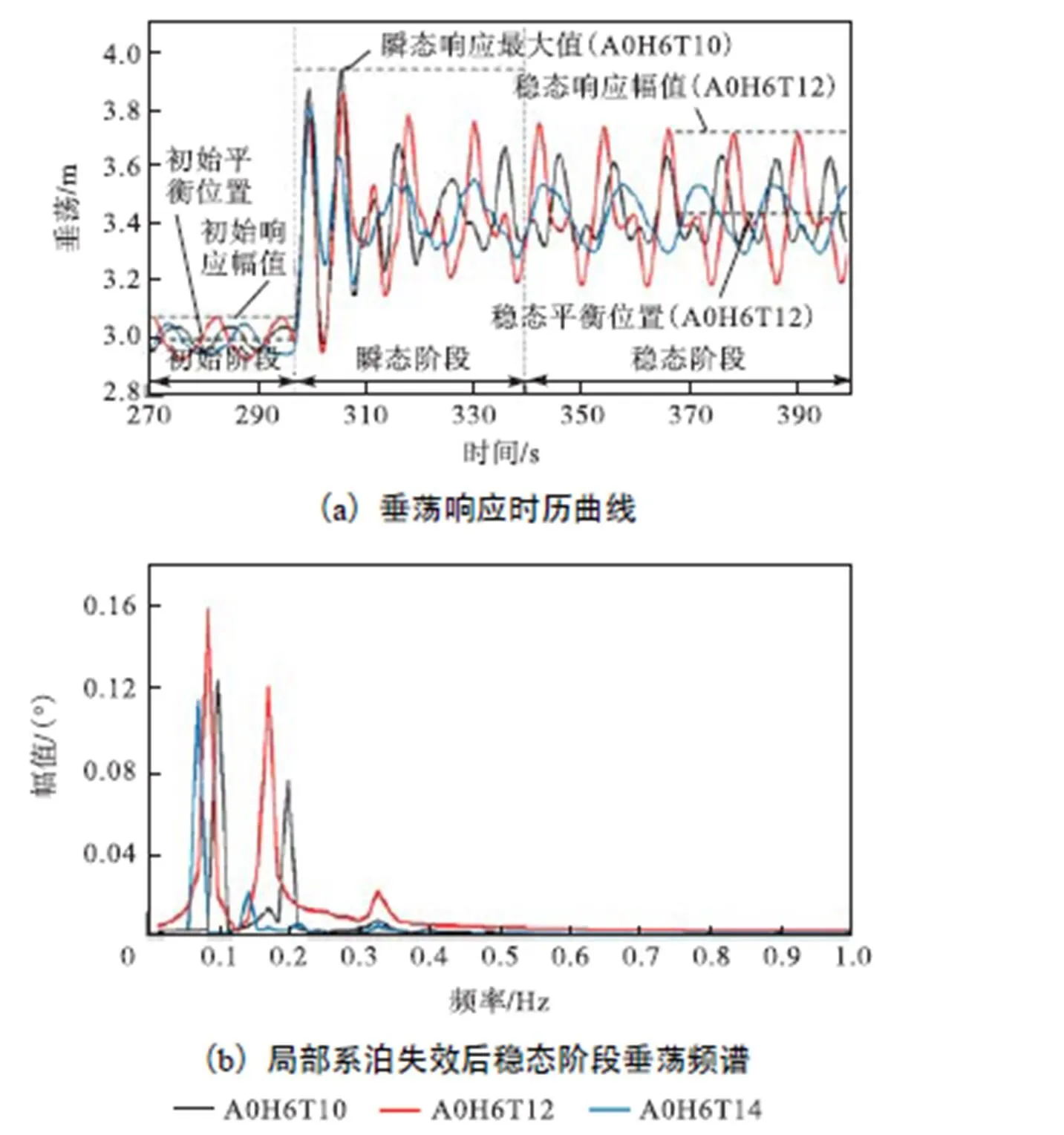
图17 不同波周期下筋腱失效过程TLP垂荡动力响应

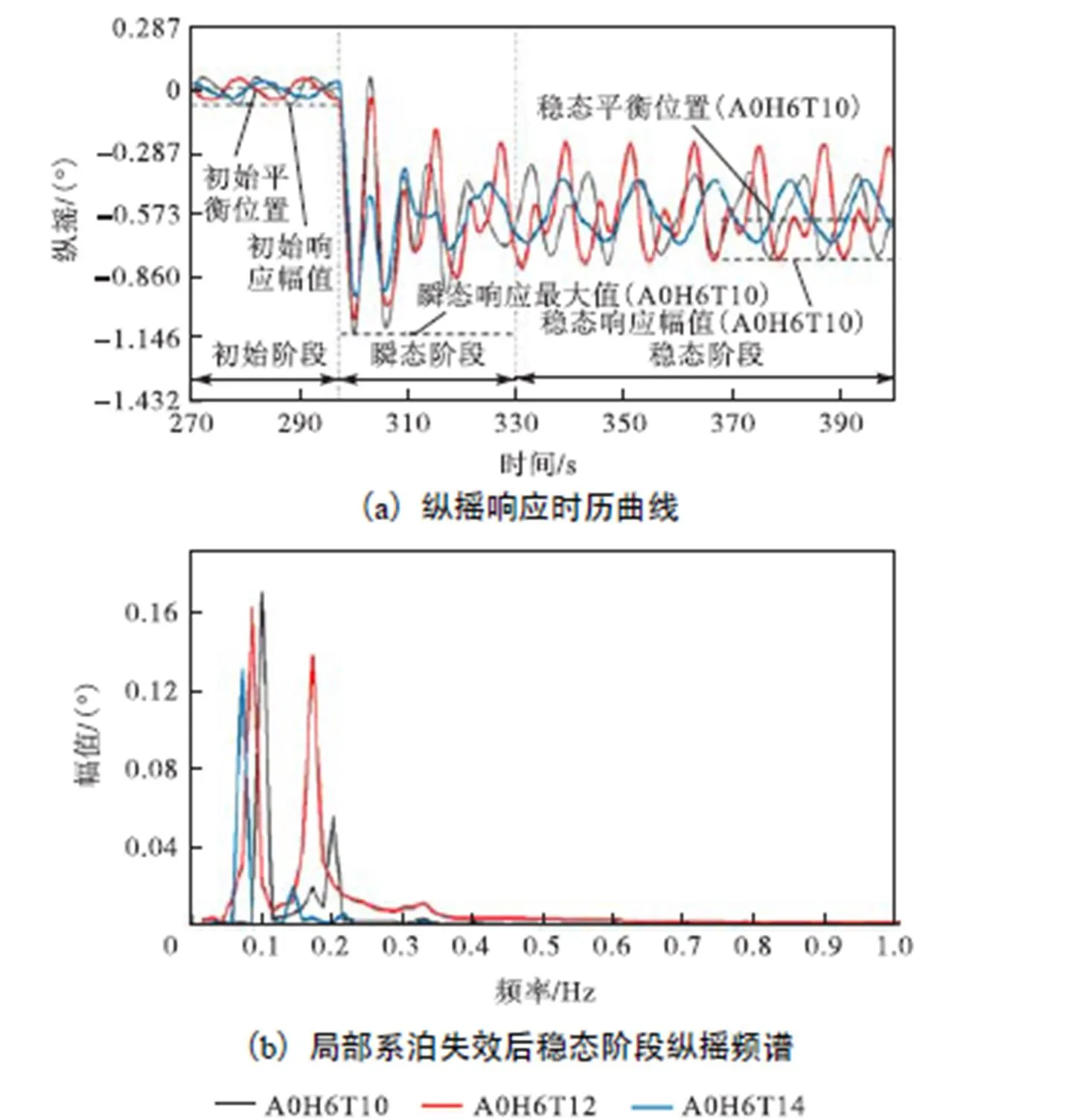
图18 不同波周期下筋腱失效过程TLP纵摇动力响应

4.3.4 不同波浪参数对筋腱顶端张力的影响

相对于平台的运动响应，筋腱张力的变化更加直接反映结构的危险状态．本次研究的筋腱采用X65钢管(参数见表1)，预张力值是1.7×107,N，在一根或多根筋腱失效后，与其紧邻的筋腱张力会激增，产生连续失效破坏，计算设置#1#2筋腱失效，研究不同波浪参数与#3、#8筋腱(紧邻失效筋腱)顶端张力最大值的关系．

图19是不同波浪载荷参数下#3和#8筋腱在整个时域分析过程中顶端张力最大值统计图，结果显示：局部筋腱失效后，不同入射角度下#3和#8筋腱顶端最大张力值几乎没有差别，也就是说，筋腱顶端张力对浪向敏感性很小；随着波高的增大，#3和#8筋腱顶端张力值逐渐增大；随着波周期的增大，#3和#8筋腱顶端张力值也逐渐递减．但是总体而言，不同波高下筋腱张力值最大仅相差7.9%,，不同波周期下筋腱张力值最大相差9.2%,，说明不同波浪载荷参数对筋腱顶端张力的影响较小．

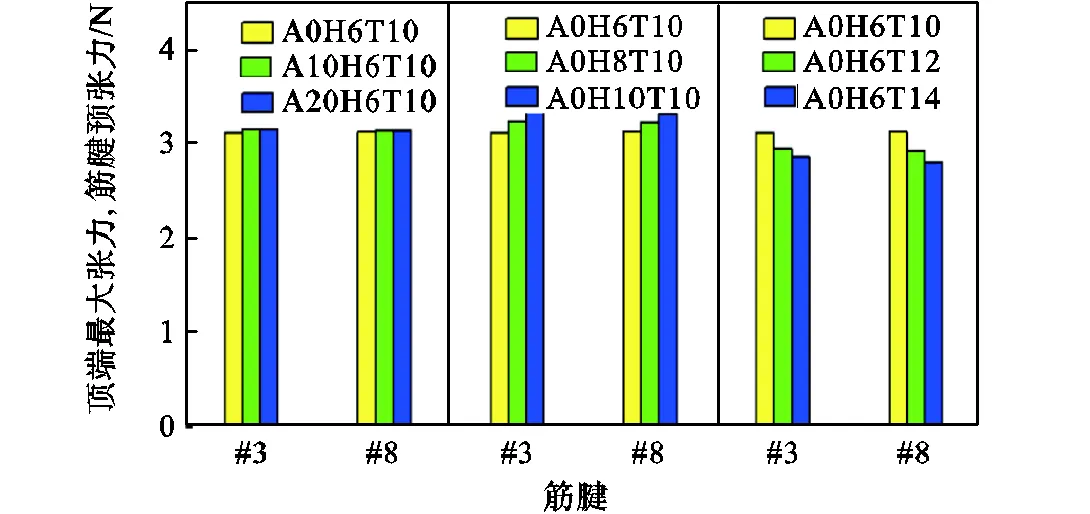
图19 不同波浪载荷参数下筋腱顶端张力统计值

图20是不同波浪载荷参数下平台垂荡瞬态响应最大值统计，可以发现，在不同浪向、波高和波周期参数下，垂荡瞬态响应最大值与剩余筋腱顶端最大张力值的变化规律完全一致，充分体现了垂荡与顶端张力的强相关性．

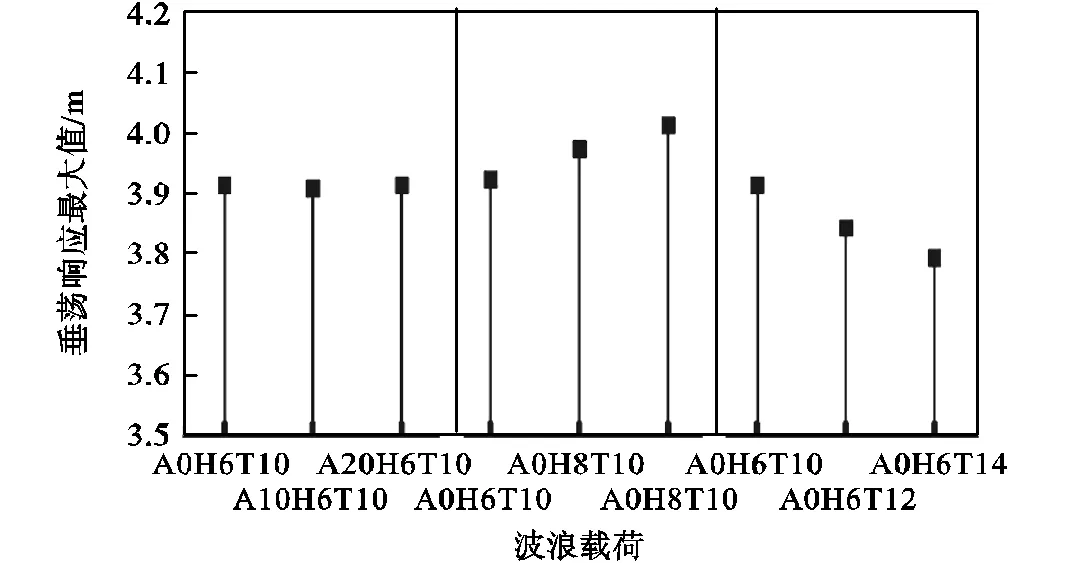
图20 不同波浪载荷参数下平台垂荡响应统计值

5 结 论

针对拥有8根筋腱的经典张力腿平台结构，在规则波下采用时域分析方法，对局部系泊失效后张力腿平台动力响应和系泊特性开展了研究，主要结论如下.

(1) 由于TLP在平面内的运动响应具有顺应性特征，局部系泊失效后，横荡、纵荡和艏摇自由度的瞬态响应并不明显，部分筋腱组合失效引起的瞬态效果在时间上具有一定的滞后性．

(2) 系泊系统为垂荡、横摇和纵摇自由度提供主要刚性约束，所以局部系泊失效后，这3个自由度的瞬态效果明显；失效筋腱位置越集中，TLP响应越大，失效筋腱位置越分散，TLP响应越小．

(3) 系泊系统完好时，TLP艏摇响应远小于横摇、纵摇响应；部分筋腱组合失效后，由于筋腱失效位置及环境载荷作用方向等不对称因素，TLP艏摇响应最大值激增，数值接近横摇和纵摇响应的数量级．

(4) 局部系泊失效后，平台垂荡瞬态阶段响应对波高和波周期敏感性较强，稳态阶段响应对浪向、波高和波周期敏感性较强；纵摇(横摇)瞬态和稳态阶段响应对浪向、波高和波周期敏感性均较强．

(5) 波高越大，波浪周期越小，在时域分析中剩余筋腱顶端张力最大值越大，但总体而言，波浪参数对筋腱顶端张力的影响较小；筋腱顶端张力与平台垂荡响应有强相关性．

［1］ API(American Petroleum Institute). Draft Recommended Practice 2,T，Rev. 3. Planning，Designing，and Constructing Tension Leg Platforms[S]. Washington，DC：API，2007.

［2］ Jameel M，Oyejobi D O，Siddiqui N A，et al. Nonlinear dynamic response of tension leg platform under environmental loads[J]. KSCE Journal of Civil Engineering，2017，21(3)：1022-1030.

［3］ Oyejobi D O，Jameel M，Sulong N H R. Nonlinear response of tension leg platform subjected to wave，current and wind forces[J]. International Journal of Civil Engineering，2016，14(8,A)：521-533.

［4］ 谷家扬，杨建民，吕海宁. 考虑风浪流的TLP张力腿张力响应规律分析[J]. 船舶力学，2012，16(9)：1041-1055. Gu Jiayang，Yang Jianmin，Lü Haining. Comprehensive study on tendon tension of TLP considering wind，wave and current[J]. Journal of Ship Mechanics，2012，16(9)：1041-1055(in Chinese).

［5］ Gu Jiayang，Yang Jianmin，Lu Haining. Studies of TLP dynamic response under wind，waves and current[J]. China Ocean Engineering，2012，26(3)：363-378.

［6］ Tahar A，Kim M H. Hull/mooring/riser coupled dynamic analysis and sensitivity study of a tanker-based FPSO [J]. Applied Ocean Research，2003，25(6)：367-382.

［7］ Ahmad S. Stochastic TLP response under long crested random sea[J]. Computers & Structure，1996，61(6)：975-993.

［8］ Siddiqui N A，Ahmad S. Fatigue and fracture reliability of TLP tethers under random loading[J]. Marine Structures，2001，14(3)：331-352.

［9］ Yang Mindong，Teng Bin，Xiao Longfei. Full time-domain nonlinear coupled dynamic analysis of a truss spar and its mooring/riser system in irregular wave[J]. Science China Physics Mechanics & Astronomy，2014，57(1)：152-165.

［10］ Yang Mindong，Teng Bin，Ning Ding，et al. Coupled dynamic analysis for wave interaction with a truss spar and its mooring line/riser system in time domain[J]. Ocean Engineering，2012，39：72-87.

［11］ 谷家扬. 张力腿平台复杂动力响应及涡激特性研究[D]. 上海：上海交通大学船舶海洋与建筑工程学院，2013. Gu Jiayang. Study on the Complex Dynamic Response and Vortex-Induced Motion Characteristics of Tension Leg Platform[D]. Shanghai：School of Naval Architecture，Ocean and Civil Engineering，Shanghai Jiao Tong University，2013(in Chinese).

［12］ Jayalekshmi R，Idichandy V G，Sundaravadivelu R. Physical simulation of the hull-tether coupled dynamics of a deepwater TLP[C]// ASME 26th International Conference on Offshore Mechanics and Arctic Engineering 2007. Michigan：American Society of Mechanical Engineers，2007：149-157.

［13］ Mansour A M，Huang E W，Phadke A C，et al. Tension leg platform survivability analysis[C]//ASME 25th International Conference on Offshore Mechanics and Arctic Engineering. Michigan：American Society of Mechanical Engineers，2006：477-483.

［14］ Kim M H，Zhang Zhi. Transient effects of tendon disconnection of a TLP in moderate-strength hurricane conditions[J]. International Journal of Naval Architecture and Ocean Engineering，2009，1(1)：13-19.

［15］ Yang Chan K，Kim M H. Transient effects of tendon disconnection of a TLP by hull-tendon-riser coupled dynamic analysis[J]. Ocean Engineering，2010，37(8/9)：667-677.

［16］ Eatock Taylor R，Jefferys E R. Variability of hydrodynamic load predictions for a tension leg platform[J]. Ocean Engineering，1986，13(5)：449-490.

［17］ Liu Weimin. Research on time-domain dynamic response of tension leg platform in regular wave[J]. Applied Mechanics and Materials，2014，670/671：801-804，

［18］ Faltinsen Odd M. Sea Loads on Ships and Offshore Structures[M]. United Kingdom：Cambridge University Press，1993.

［19］ Chakrabarti S K. Hydrodynamics of Offshore Structures [M]. United Kingdom：WIT Press，1987.

［20］ API(American Petroleum Institute). API Recommended Practice 2,SK，Design and Analysis of Station Keeping Systems for Floating Structures[S]. 3rd Ed. Washington，DC：API，2005.

Dynamic Response Analysis of a Tension Leg Platform with Multiple Broken Tendons

Yu Jianxing1, 2，Gao Xiaodong1, 2，Yu Yang1, 2，Hao Shuai1, 2，Xu Lixin1, 2

(1．State Kay Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300350，China；2．Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai 200240，China)

In terms of the nonlinear coupling effect of a tension leg platform(TLP) hull and tendons，the dynamic response of a TLP with multiple broken tendons was analyzed using a time-domain method．The relationship among tendon failure positions，wave force parameters，and dynamic responses of six degrees of freedom was then investigated．It was found that with multiple broken tendons，the dynamic responses of sway，surge and yaw were far smaller than those of roll，pitch and heave．The tendon failure positions had close correlations with the TLP dynamic responses．The more centralized the tendon failure positions were，the higher the TLP responses were，and vice versa．As wave parameters varied，the TLP performance varied across different motion characteristics and at peak tension．The transient heave response was sensitive to wave height and wave period，while its steady-state response was sensitive to wave direction，height，period．However，the transient and steady-state responses in pitch and roll were also sensitive to wave direction，height，and period．The wave force parameters had small impact at top tension of tendon.

hull-tendon coupled dynamic analysis；multiple broken tendons；failure position；wave force parameter；dynamic response；time-domain analysis

P751

A

0493-2137(2019)01-0040-12

2018-04-11；

2018-05-16.

余建星（1958—  ），男，教授，yjx2000@tju.edu.cn.

余 杨，yang.yu@tju.edu.cn.

国家重点基础研究发展计划(973计划)资助项目(2014CB046803)；国家自然科学基金青年基金资助项目(51609169)；国家自然科学基金资助项目(51779173)；广西科技重大专项项目(桂科AA17292007).

the National Basic Research Program of China(No.,2014CB046803)，the National Natural Science Foundation of China for Youth(No.,51609169)，the National Natural Science Foundation of China(No.,51779173)，the Guangxi Science and Technology Major Project(No.,Guike AA17292007).

10.11784/tdxbz201804032

(责任编辑：王新英)