基于改进水平集的菌落图像智能计数算法
张力新,张黎明,杜培培,余 辉
基于改进水平集的菌落图像智能计数算法
张力新,张黎明,杜培培,余 辉
(天津大学生物医学检测技术与仪器重点实验室,天津 300072)
针对现有的菌落自动识别计数方法对背景敏感、对多菌种菌落分割普适性差的缺点,提出一种基于改进水平集的全自动菌落分割、计数方法.该方法利用偏置场对背景进行建模以消除背景灰度不均影响;构造含有终止条件的多相水平集算法实现菌落目标的自适应分割;通过极坐标空间中凹点检测实现粘连目标计数修正.由天津市食品安全检测技术研究院提供300例多菌种混杂菌落样本做为测试集,以专家人工鉴定结果为金标准,将本方法与传统形态学方法、迅数icount10两种定量方法进行对比,菌落密度在300CFU内时,本方法计数准确率达到92.7%,对多菌种混杂菌落的计数精度、分割效果都优于其他两种方法.
偏置场;多相水平集;凹点检测;菌落计数
菌落是细菌在一定的pH值、温度下,通过一定时间在合适的培养基中形成的能被视觉识别的生长物.对培养成型的菌落的检测能在很大程度上反映食品、药品、水质等是否符合安全标准要求[1].自动菌落检测技术可以大幅降低质检员的工作强度,提升检测的准确率和工作效率.根据我国菌落计数标准GB4789.2—2016,当样本菌落密度在300CFU以下时,自动与手动计数的结果偏差不应超过15%[2].
目前市面上已经有了一些比较成熟的菌落自动检测仪器,比如法国Interscience公司的Scan系列、杭州迅数Icount系列等.国内外学者也提出了多种菌落图像自动分割、检测方法.
(1) 融合距离变换、分水岭分割及极限腐蚀等形态学处理的传统计数算法[1,3-4].该类算法可以实现粘连菌落的分割,提高了计数精度,但其仅对单一菌种、规则大小的类圆型菌落计数效果较好,对于背景噪声严重、多菌种混杂的菌落样本容易造成过分割和欠分割.
(2) 活动轮廓检测算法[5]可以适用于背景灰度不均匀、边缘较弱的类圆粒目标的分割,但其在边缘检测之前需要单独提取每个检测目标进行增强处理,增加了计算的复杂性,且对较小的棒状菌落分割效果较差.
(3) 基于深度学习的图像分割方法[6-7],如全卷积神经网络(FCN)以及其分支Unet网络等新兴技术,近些年来被大量应用于图像分割问题,但其需要数量庞大的数据作为训练集,在实际菌落数据采集时有很大难度,且其分割的核心思想是对每个像素进行分类,没有充分考虑像素与像素之间的关系,忽略了在通常基于像素分类的分割方法中使用的空间规整步骤,缺乏空间一致性.
(4) 水平集算法[8-9]的核心思想是将平面中二维闭合曲线的演化问题转换成为比其高一维的三维空间中水平集函数的演化,再用一些现有的数学方法解决图像分割问题,包括变分法、解偏微分方程(PDE)等.其主要优势在于:避免参数化的困难,能处理图像拓扑结构发生变化的情况,对图像噪声的鲁棒性 更好.
目前菌落计数软件普遍存在智能化程度低,算法鲁棒性差的问题.尤其对于多菌种混杂菌落这种背景灰度不均匀、大小形态差异较大的样本,分割效果不理想.Li等[10]提出了一种基于偏置场矫正的区域水平集算法,该方法对参数初始值不敏感且算法鲁棒性较好,在MRI背景建模的应用中取得了较为理想的效果.但该方法直接用于菌落计数时存在两类问题:①无法实现粘连菌落目标的自动分割;②迭代次数需人工设置,算法演化终止条件不明确,对于目标形态差异较大的不同样本难以实现自适应分割.
针对上述算法种存在的这些问题,本文提出了一种改进的水平集和极坐标空间下凹点检测相结合的自动分割计数算法.该算法引入含有偏置场矫正的三相水平集分割算法以消除背景灰度影响、提升小目标和弱边缘目标的分割精度;构造封闭区域面积信息为主要判据的终止条件,以实现不同样本的自适应分割;设计极坐标空间下检测凹点模块,以实现粘连菌落的二次分割,提升计数精度.本文算法全程无需人工干预,即可实现菌落图像的全自动分割和计数.
1 水平集分割
1.1 水平集建模
由于受到培养皿反射光、边缘阴影和培养基颜色等因素的影响,培养皿内影像灰度并不均匀.此外,各个菌落灰度值及形态差异很大.为了排除背景阴影的干扰、提高较小目标和弱边缘目标的分割精度,同时兼顾算法效率,本文将背景灰度影响考虑为图像成分进行矫正,并选用了三相水平集.
首先,对图像进行建模得

根据上文建模,以K-means聚类算法为核心,建立三相水平集的能量泛函方程如下,通过最小化此能量泛函可得到分割结果为

式(2)等号右边的第2和第3项为能量函数的正则项,其中第2项用来计算0水平集的弧长,保持迭代过程中0水平集边界的平滑性;第3项为距离正则项,其实质为一个惩罚函数,用来维持水平集函数在更新过程中0水平集周围的符号距离函数性质,确保水平集函数更新的稳定,避免了水平集函数的重新初始化[11].


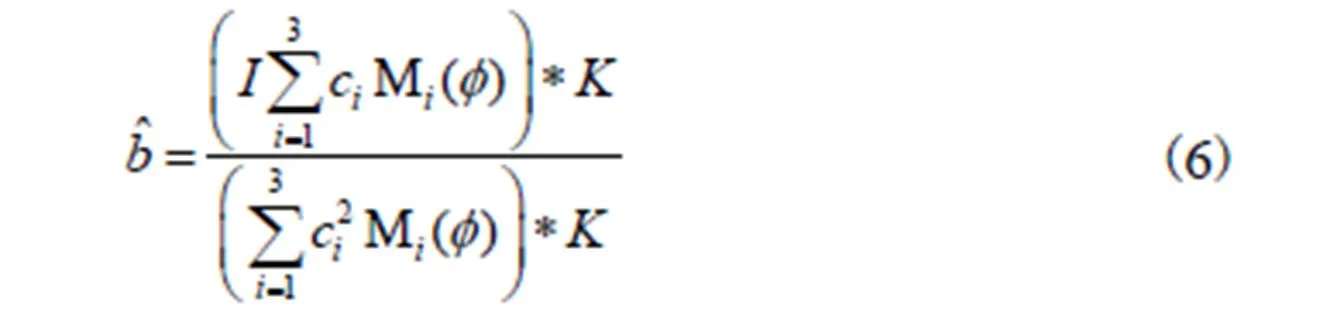
1.2 终止条件
经过数次的迭代后,前面建立的模型能较准确地将菌落目标分割出来,但在实际采集到的数据中,不同样本间菌落的分布情况、大小形态等都存在着较大差异,所以很难固定一个适用于所有样本的迭代次数.因此,本文在上述算法的基础上引入迭代演化的终止条件,以实现目标的自适应分割.
2 菌落计数
使用上述水平集模型对菌落图像样本分割之后,结果如图1所示.可以看出,各类菌落轮廓都被准确地分割出来,但通过局部放大图可以看出,菌落之间还存在着粘连的问题,会影响后续的计数精度.因此,需要将粘连的菌落分割开来.

图1 水平集分割结果及粘连部分
经观察发现,粘连菌落上存在着明显的凹点.因此,只需要判断菌落轮廓上是否存在两个或以上的明显凹点,即可检测出粘连目标.本文设计了一种基于极坐标变换的凹点检测算法,步骤如下.

部分粘连菌落的分割效果如图2所示,可以看出粘连的部分被有效地分开.在实现粘连菌落的分割后,采用四邻域标准遍历搜索出分割结果中所有的连通域,对每个连通域进行排序标记即可实现菌落的计数(图3).

图2 粘连菌落目标分割

图3 菌落计数结果
3 实验结果与分析
3.1 实验数据

3.2 实验步骤和参数设置
算法整体流程如图4所示.其中预处理步骤主要包括图像灰度化和培养皿内区域选取(图5).首先将一副RGB三通道彩色菌落图像转换到HSV空间,以V分量构建灰度图像[12],接着去除掉不属于检测有效区域的培养皿边缘及外围区域.本文采用的去除方法是首先对二值化后的菌落图像进行形态学膨胀运算,以获得不含孔洞和噪声的培养皿大致轮廓;随后求该连通域的质心,以此质心到边缘的最小距离为半径作圆,即可得到一个有效的圆形掩模,用以去除圆外区域,获得理想的培养皿内部区域.
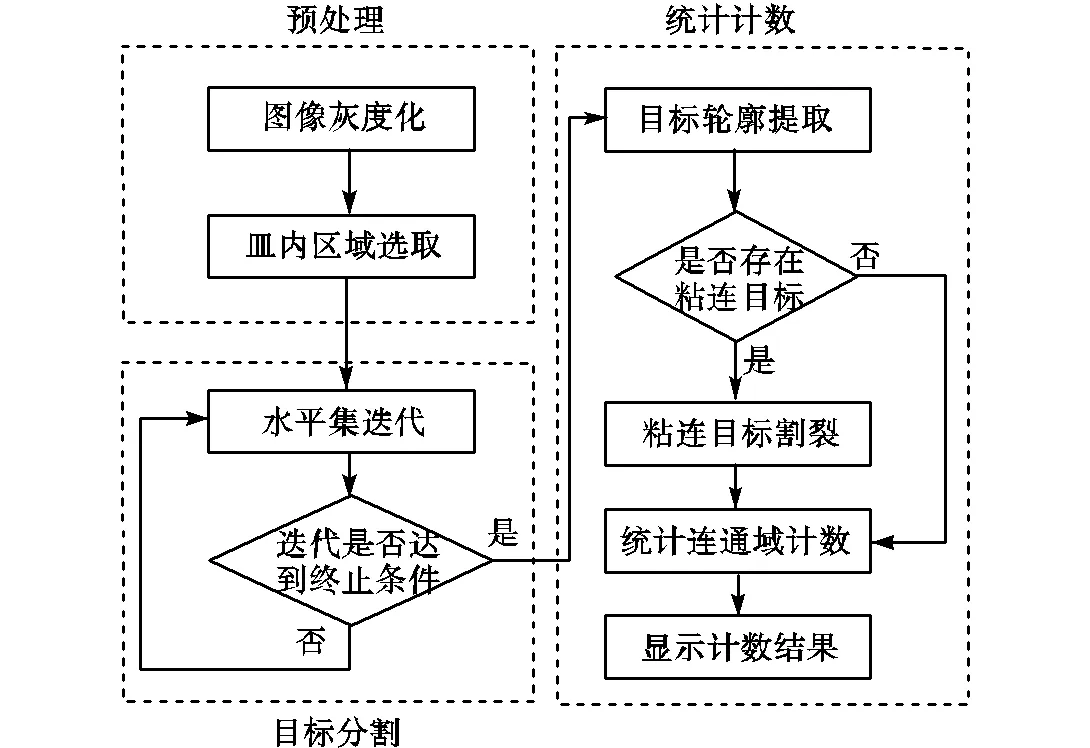
图4 分割计数算法流程
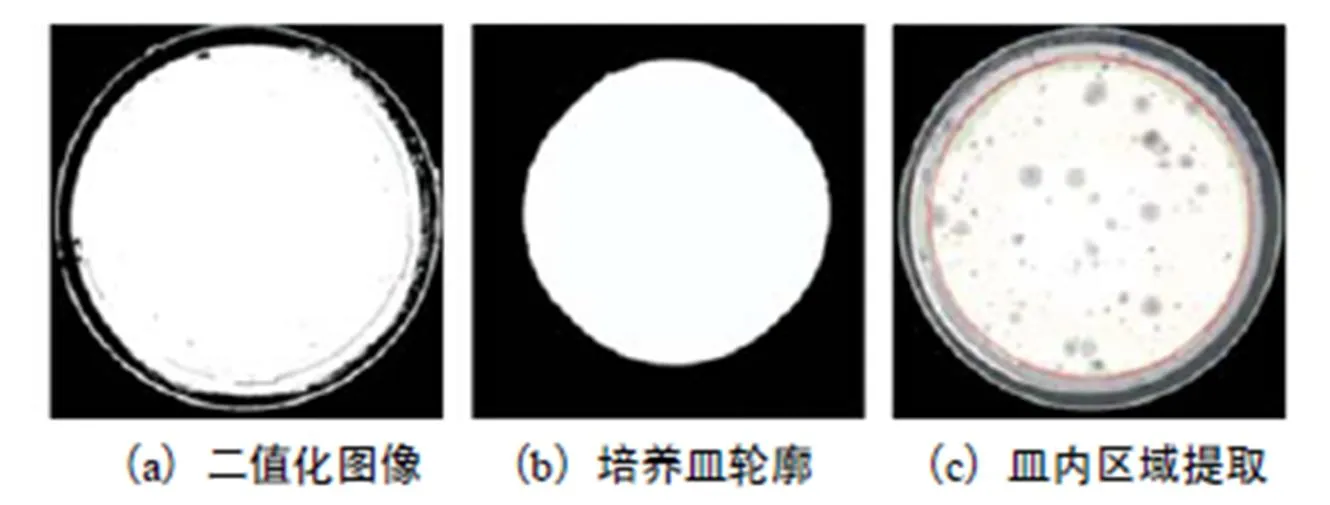
图5 图像预处理及培养皿内区域提取
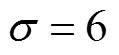
3.3 实验结果
本文通过实验从分割结果和计数精度两方面验证算法效果,所有样本的标准结果由天津食检院专家人工标定给出.
将本文算法与RSF水平集算法[13]、杭州迅数公司icount10菌落分析算法进行分割结果对比,图6分别列出了3种算法的分割结果.接着本文用不同区间共20个批次、总计300个多菌种菌落样本对比了本文算法、传统形态学方法、迅数icount10的计数结果准确度.表1表现了在不同菌落密度区间下3种方法的计数精度统计结果,图7显示了不同密度区间下3种算法计数结果的平均误差曲线.可以看出,随着菌落密度的增加,3种算法的计数误差显著增大,这主要是因为有一部分菌落分布于琼脂夹层中和培养皿的边缘部分,无法在二维的数字图像上反映出来.
3.4 结果分析
由图6(a)可见,使用RSF水平集模型分割,分割结果包含大片的非菌落目标区域,这是因为RSF水平集模型将图像背景中大片的灰度不均匀区域作为目标分割了出来;图6(b)为迅数icount10算法的分割结果,可见该算法对于大部分灰度值较高、面积较大的类圆形菌落目标分割效果较好,但通过图6(b)中标记可以看出,仍有部分目标的分割不够准确,且该算法基本无法分割灰度值较低、面积较小的菌落目标,这主要是因为该算法会将和背景灰度较为接近的小目标当作背景噪声筛除掉.与前两种算法相比,本文算法(图6(c))准确地找到了所有的菌落目标,并且分割边缘较为平滑,经专家鉴定,本文分割结果与实际菌落边缘基本一致.
表1 不同误差、密度区间下各算法样本数统计

Tab.1 Number of samples statistics of each algorithms in different error and density ranges
注:逗号前为统计样本数,逗号后为样本占比.
由表1和图7可见,在菌落密度较小的样本中,3种算法都能达到符合国家标准的计数精度,但随着菌落密度的增加,本文算法计数精度要明显优于迅数icount10算法和传统的形态学方法;当菌落样本密度达到200~300CFU时,本文算法精度优势尤其明显.这是因为随着菌落密度的增加,图像中含有更多小型、模糊的菌落目标,且粘连菌落目标的数目显著增多,导致计数结果发生偏差.
本文提出的改进水平集模型和极坐标凹点检测相结合的菌落分割计数方法,相比之前的传统形态学方法、RSF水平集和迅数icount10算法,具有更高的分割精度和计数准确率,其主要原因是:本文方法采用偏差矫正有效消除了灰度不均匀的背景对菌落目标分割带来的干扰,又通过引入基于面积信息的终止条件有效地解决了传统水平集算法人工干预程度高、分割边缘不够准确的问题;同时,本文采用极坐标空间凹点检测方法,有效地识别出了粘连菌落并将其分割,提升了后续计数的精度.

图6 3种算法分割的结果
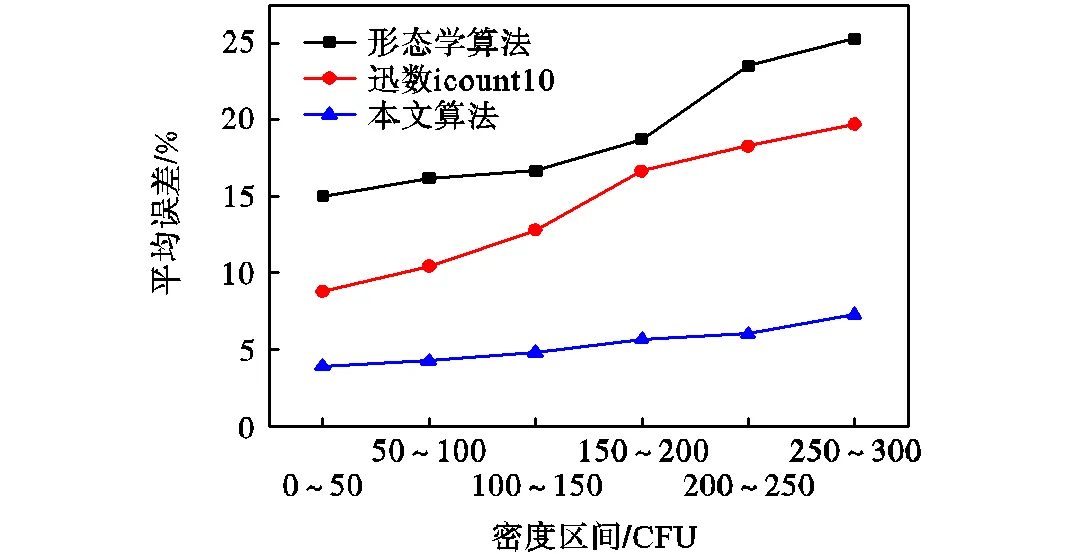
图7 各算法在不同密度区间下计数平均误差
4 结 语
针对现有图像处理方法对多菌种混杂的复杂菌落样本分割不够精准、计数误差大的问题,本文首先去除采集到菌落图像的培养皿外区域,排除外区域的干扰;然后用背景灰度偏差矫正的三相区域水平集方法对菌落图像进行分割,得到包含粘连目标的菌落轮廓;再对每个菌落轮廓进行极坐标凹点检测,判断其是否存在粘连情况并将粘连轮廓从凹点处进行分割;最后通过连通域的依次标记实现菌落的计数.实验结果表明,该算法在分割、计数等方面的效果都优于传统的菌落识别算法,计数结果误差小于10%,且不受图像背景灰度情况、菌落大小和形态等条件影响,能实现菌落的全自动分割和计数.同时,该算法也适用于其他类圆粒目标的自动识别,能有效提升其分割、计数的准确性.
[1] 陈可意. 菌落计数与分类智能算法研究[D]. 天津:天津大学精密仪器与光电子工程学院,2014. Chen Keyi. Study on Intelligent Algorithm of Colony Counting and Classification[D]. Tianjin:School of Precision Instrument and Opto-Electronics Engineering,Tianjin University,2014(in Chinese).
[2] 中华人民共和国卫生部. GB4789.2 食品安全国家标准[S]. 北京:食品微生物学检验,2016. Ministry of Health of the People's Republic of China. GB4789.2 National Food Safety Standard[S]. Beijing:Microbiology Detection,2016(in Chinese).
[3] 尹诗白. 基于模糊集合理论的颗粒目标分割和识别[D]. 西安:长安大学,2013. Yin Shibai. Segmentation and Recognition of Particle Object Based on Fuzzy Set Theory[D]. Xi’an:Chang’an University,2013(in Chinese).
[4] 司秀娟,王红强,宋良图. 基于图像处理的菌落自动计数系统[J]. 北京生物医学工程,2017,36(6):633-638. Si Xiujuan,Wang Hongqiang,Song Liangtu. Automatic colony counting system based on image processing[J]. Beijing Biomedical Engineering,2017,36(6):633-638(in Chinese).
[5] 武宗茜,王 鹏,丁天怀. 活动轮廓模型在重叠藻细胞计数中的应用[J]. 计算机工程,2012,38(3):209-211.Wu Zongqian,Wang Peng,Ding Tianhuai. Application of active contour model in overlapped algae cells counting[J]. Computer Engineering,2012,38(3):209-211(in Chinese).
[6] Dorbe N,Jaundalders A,Kadikis R,et al. FCN and LSTM based computer vision system for recognition of vehicle type,license plate number,and registration country[J]. Automatic Control & Computer Sciences,2018,52(2):146-154.
[7] 朱翔宇. 基于卷积神经网络的肺部结节检测系统研制[D]. 南京:南京大学,2017. Zhu Xiangyu. The Research of a Pulmonary Nodule Detection Method Based on the Conventional Neural Network[D]. Nanjing:Nanjing University,2017(in Chinese).
[8] Roy K,Bhattacharya P,Suen C Y. Towards nonideal iris recognition based on level set method,genetic algorithms and adaptive asymmetrical SVMs[J]. Engineering Applications of Artificial Intelligence,2010,24(3):458-475.
[9] 吴永飞. 图像分割的变分模型及数值实现[D]. 重庆:重庆大学,2016. Wu Yongfei. Variational Model and Numerical Implementation of Image Segmentation[D]. Chongqing:Chongqing University,2016(in Chinese).
[10] Li C,Huang R,Ding Z,et al. A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI[J]. IEEE Transactions on Image Processing,2011,20(7):2007.
[11] Li C,Xu C,Gui C,et al. Distance regularized level set evolution and its application to image segmentation[J]. IEEE Transactions on Image Processing,2010,19(12):3243-3254.
[12] 张国权,李战明,李向伟,等. HSV空间中彩色图像分割研究[J]. 计算机工程与应用,2010,46(26):179-181. Zhang Guoquan,Li Zhanming,Li Xiangwei,et al. Research on color image segmentation in HSV space[J]. Computer Engineering and Applications,2010,46(26):179-181(in Chinese).
[13] Li C,Kao C Y,Gore J C,et al. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Transactions on Image Processing,2008,17(10):1940-1949.
Intelligent Counting Algorithm for Colony Image Based on Improved Level Set
Zhang Lixin,Zhang Liming,Du Peipei,Yu Hui
(Key Laboratory of Biomedical Testing Technology and Instruments,Tianjin University,Tianjin 300072,China)
The current colony counting methods are sensitive to background and are inefficient from the viewpoint of the universality of multi-species colony segmentation. To overcome this limitation,an automatic colony segmentation and counting method based on an improved level set is proposed. Here in,the bias field is used to model the background to eliminate the influence of intensity inhomogeneity. A multiphase level set algorithm with termination condition is constructed to realize adaptive segmentation of colony target. Through the concave point detection in polar coordinates,the correction of adhesion targets counting is achieved. The algorithm is tested on 300samples of multi-species colonies provided by Tianjin Food Safety Inspection Technology Research Institute. The algorithm is compared with two quantitative methods:traditional morphological algorithm and Shineso icount10 algorithm,and the results of expert artificial identification are used as gold standards. When the colony density is under 300CFU,the counting accuracy rate is up to 92.7%. Both the counting accuracy and segmentation effect of multi-species colonies using the proposed method are superior to those of the other two algorithms.
bias field;multiphase level set;concave point detection;colony counting
TP391.41
A
0493-2137(2019)01-0084-06
2018-04-18;
2018-09-10.
张力新(1963— ),男,硕士,研究员,lxzhang@tju.edu.cn.
余 辉,yuhui@tju.edu.cn.
国家自然科学基金资助项目(61475116);天津市科技支撑资助项目(16YFZCNC00690,16ZXCXSF00040);天津市北辰区科技发展计划资助项目(D-2017-NYKJXM-08).
the National Natural Science Foundation of China(No.61475116),the Tianjin Science and Technology Program(No.16YFZCNC 00690,No.16ZXCXSF00040),the Tianjin Beichen District Science and Technology Development Project(No.D-2017-NYKJXM-08).
10.11784/tdxbz201804071
(责任编辑:孙立华)

