基于AR模型和卡尔曼滤波的UWSNs节点分层预测定位

刘丽萍，操刘生，陈 梦



基于AR模型和卡尔曼滤波的UWSNs节点分层预测定位

刘丽萍，操刘生，陈 梦

(天津大学电气自动化与信息工程学院，天津 300072)

水下无线传感器网络(UWSNs)拓扑变化频繁，通信能力有限，给水下环境监测网络中的节点定位技术带来很大挑战．近海环境监测中，考虑到节点随着洋流移动并呈现出半周期性，利用节点运动模型，设计了基于 AR 模型和卡尔曼滤波的 UWSNs 节点分层预测定位方法(HPLM-AK)．建立了锚节点速度的 AR 预测模型，综合考虑网络能量消耗和定位精度的需求，进一步建立了锚节点速度的状态方程和观测方程，利用卡尔曼滤波算法实现对锚节点速度的最优估计，进而提高了定位精度且降低了网络通信能耗；普通节点利用与锚节点运动的空间相关性，根据参考节点的速度和位置信息估算自身的速度并结合上一时刻的位置信息完成定位．考虑到提高节点的定位覆盖度，设计了节点的定位置信度，并通过将置信度较高的普通节点升级为参考节点的方式来弥补锚节点稀疏的不足．同时，设计了参考节点列表更新机制，通过更新参考节点的信息，普通节点选取置信度较高的参考节点来参与自身的定位，提高了预测定位精度．本文以E117.25°～E132.20°、N24.00°～N43.45°洋流数据为实验背景对算法进行了仿真，并且与可扩展的移动预测定位(SLMP)方法进行了分析比较，仿真结果表明，HPLM-AK方法提高了定位覆盖度和定位精度，且降低了网络的通信能耗．

水下传感器网络；AR模型；卡尔曼滤波；参考节点列表；分层预测定位

水下无线传感器网络(underwater wireless sensor networks，UWSNs)在海洋环境监测、洋流数据采集、海域资源勘测、海啸预警等应用方面有着不可替代的价值[1]．实际应用中，传感器节点的位置是网络收集有效信息的基础．水下环境中，传感器网络拓扑随着洋流运动不断改变，通信信号衰减快、带宽窄，这些因素都极大地影响水下传感器节点定位的精度.

提高定位精度、降低网络通信能耗是水下无线传感器网络定位方法的设计目标．区域定位机制(area-based localization scheme，ALS)[2]中提出了无需测距的区域定位机制，锚节点通过发送不同能级的数据将网络划分为不同的区域，待定位节点将接收到的锚节点信息以及相应的能级发送给汇聚节点，汇聚节点根据已知锚节点信息来定位未知节点，但算法的通信能耗较高．为减少网络通信开销，运动感知的自定位(motion-aware self-localization，MASL)方法[3]设计了集中式定位算法，在汇聚节点处计算位置信息，降低了各个节点的计算负荷，整体网络能耗降低，但定位实时性不足．考虑大规模网络中，信标节点的数量有限，大规模水下网络定位机制(localization scheme for large scale underwater networks，LSLS)[4]提出了将已经定位的节点升级为参考节点来辅助未知节点定位的方法，该方法在一定程度上提高了定位覆盖度．为提高节点的定位精度，基于粒子群优化的移动预测定位(localization method based on mobility prediction and partial swarm optimization algorithms，MP-PSO)[5]采用粒子群算法优化锚节点位置坐标，但锚节点周期性优化坐标信息增加了网络通信能耗，对能量受限的网络带来很大的挑战．可扩展的移动预测定位(scalable localization with mobility pattern，SLMP)[6]算法提出利用预测运动模型来估计位置，根据节点预测位置与实际位置的差值是否超过某一阈值来更新运动模型，网络通信能耗较低．

综合考虑通信能耗和定位精度，结合节点的运动规律，本文提出了基于AR模型与卡尔曼滤波的UWSNs节点分层预测定位方法(hierarchical prediction localization method based on AR model and Kalman algorithm，HPLM-AK)．利用AR模型建立锚节点速度的状态方程和观测方程，通过卡尔曼递推方程对锚节点的速度信息做出最优估计，进而对锚节点进行预测定位；在普通节点定位过程中，利用普通节点和锚节点运动的空间相关性，结合锚节点的运动信息，实现普通节点的预测定位．以MITgcm 模型[7]下获得的E117.25°～E132.20°，N24.00°～N43.45°海域的环境数据为基础进行了仿真分析；仿真结果显示，定位覆盖度、平均定位误差和平均通信能耗均优于SLMP算法．

1 网络结构及节点运动方程

本文考虑分层的水下无线传感器网络拓扑，如图1所示．节点包括信标节点、锚节点以及普通节点3种类型．漂浮在水面的信标节点装有GPS设备，能够直接与卫星通信进行定位；锚节点具有较强的通信能力和计算能力，能够通过与信标节点通信进行自定位；普通节点由于能量有限，通信能力弱，只能通过与锚节点通信来进行定位．

在近海区域，潮汐是影响网络节点运动的主要因素．节点的速度由均匀振荡的潮汐场和顺时针及逆时针交替构成无穷序列的剩余场组成[8]，如图2呈现确定的半周期性，因此能够根据历史数据进行线性预测．本文假定所有节点带有深度传感器，能够获得在深度方向的位置信息，仅考虑二维平面上的节点．节点采用周期性定位算法，其预测定位方程为

将式(1)离散化，可得节点的预测定位方程为

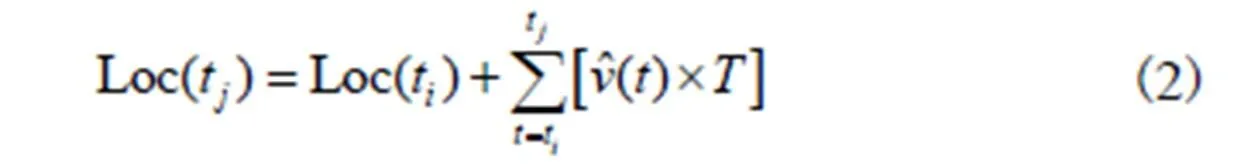
（a）方向速度

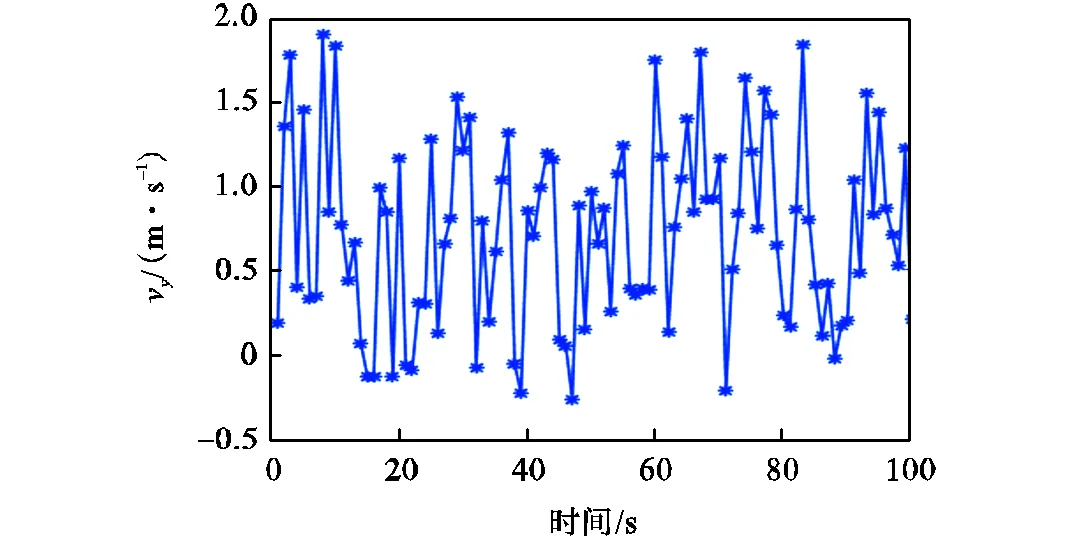
（b）y方向速度

2 节点分层预测定位

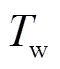
2.1 锚节点混合预测定位

考虑到减小网络开销，降低通信能耗，通过建立锚节点的运动模型来对锚节点进行预测定位．时间序列分析理论能够利用样本所具有的时序性和自相关性来建立预测模型，因此可以利用AR模型构建关于锚节点速度变化规律的运动模型，但考虑到实际应用中水下节点的有限存储能力，节点根据有限的样本并不能够建立起高精度的预测模型．同时，由于水下环境存在动态噪声，导致预测的结果并不准确．卡尔曼滤波算法[10]能够利用状态方程的递推性以及线性无偏最小均方差估计准则，结合观测值对状态估计值进行实时修正，依靠递推方程来消除随机干扰．卡尔曼滤波算法在没有提高锚节点运动模型阶次的情况下，提高了锚节点速度的预测精度．本文将AR模型与卡尔曼滤波算法相结合来建立锚节点的运动模型进行预测定位，根据AR模型建立卡尔曼滤波算法的状态方程和观测方程，通过卡尔曼递推算法对锚节点的速度做出最优估计．

2.1.1 锚节点运动模型

在锚节点速度预测过程中，利用高阶AR()模型来建立卡尔曼滤波算法的状态方程和观测方程．AR模型为

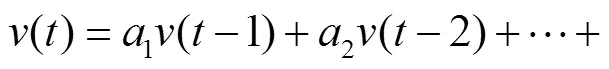
令＝＋1可得

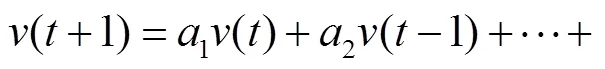
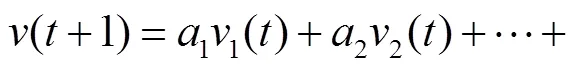
锚节点速度的观测方程为

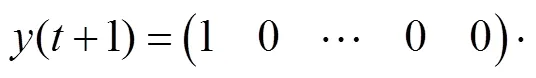
将锚节点速度的状态方程(7)和观测方程(8)代入卡尔曼递推方程组(9)，可获得锚节点速度的最优估计．

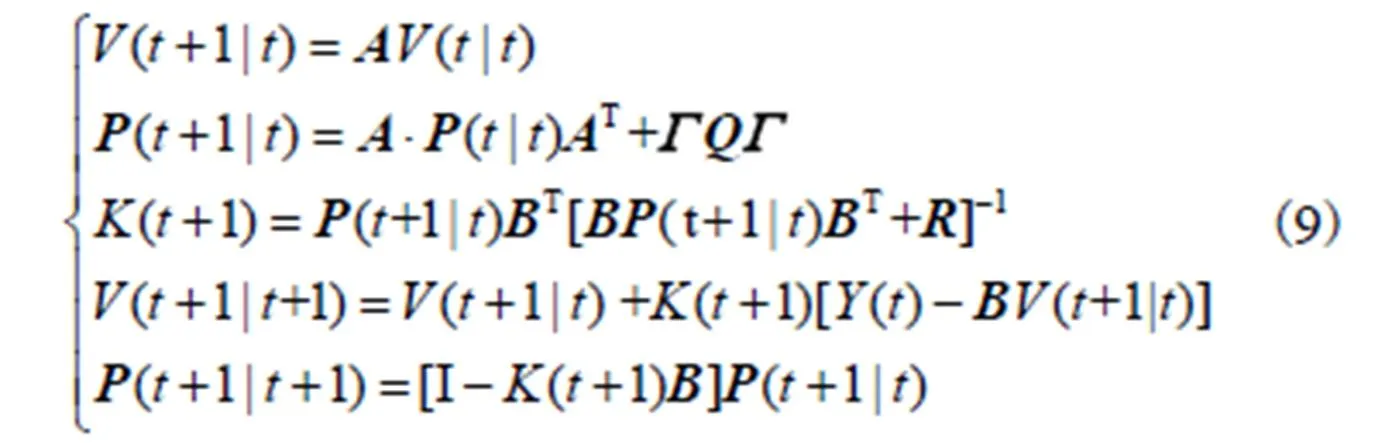
2.1.2 锚节点位置预测

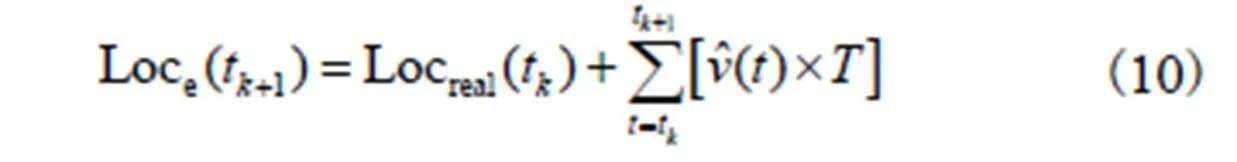
在定位过程中，考虑到定位精度，将锚节点的预测位置和测量位置进行比较，如果定位误差小于阈值，锚节点就会将当前的位置信息以及预测速度信息发送给普通节点，否则，锚节点会重新计算时间窗口内的运动信息，并将更新后的位置信息和预测速度信息发送给普通节点．锚节点发送给普通节点的数据包结构如图3所示．

节点ID时间戳速度向量位置置信度

2.2 普通节点定位

2.2.1 普通节点运动模型

则普通节点的运动模型为

2.2.2 普通节点预测定位

在普通节点定位过程中，如果普通节点接收到来自参考节点的信息，就利用接收到的参考节点的信息来更新移动模型(12)完成节点速度预测，利用式(13)实现普通节点的位置预测．否则就利用上一时间窗口的位置和估计速度来更新当前时刻的位置．

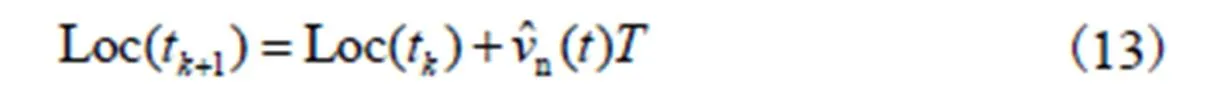
2.2.3 普通节点的参考列表更新机制

在锚节点稀疏的水下传感器网络中，综合考虑网络的定位精度和覆盖度，设计了精度较高普通节点升级为参考节点辅助定位的方法．引入普通节点的置信度作为升级为参考节点的衡量标准，其表达式为

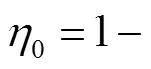
当普通节点的置信度高于某一阈值时，节点升级为邻居节点的参考节点，并将自身的位置、速度信息、置信度广播给邻居节点．节点收到新的参考节点信息时，会根据参考节点的置信度和实时性确定该参考节点参与定位的权重．参考节点的定位权重定义为

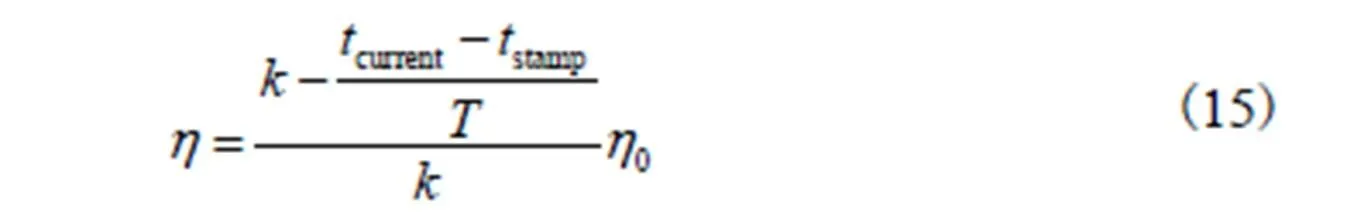
参考节点的定位权重除了和定位置信度有关外，还和时间密切相关，当前时间与确定节点置信度的时间间隔越大，该参考节点参与普通节点定位的权重越低；对于相同置信度的参考节点来说，参考节点的时间戳越接近当前时间，其定位权重值越高．

参考列表更新机制具体步骤如下.

步骤1普通节点S接收到邻居节点S的信息后，判断S是否已经在参考列表中，如果已存在，S更新参考列表中关于S的信息；否则，进入步骤2．

步骤2判断S的参考节点列表中是否有空闲位置，若有，则将节点S的信息添加到列表中的空闲位置；否则，遍历S的参考节点列表，当且仅当节点S的置信度大于参考列表中置信度最小的参考节点时，节点S的信息替换该参考节点．

步骤3S的参考节点列表中某个参考节点在小于个定位周期内没有给S发送任何信息，那么根据式(15)重新计算该参考节点的置信度；否则，将该参考节点信息已失效，从列表中删除该参考节点．

3 仿真与分析

3.1 实验参数设置

本文以MITgcm模型获得的E117.25°～E132.20°、N24.00°～N43.45°海域的环境数据为基础，用HPLM-AK定位方法对100m×100m×100m区域内的500个传感器节点进行了仿真分析，并与SLMP方法进行了比较．具体仿真参数设置如表1所示．

表1 实验仿真参数

Tab.1 Simulation parameters of experiment

3.2 算法评价标准

根据水下定位的实际情况，本文考虑定位覆盖度、平均定位误差、平均通信能耗3个定位指标．

(1)定位覆盖度：定位误差(节点的预测位置与真实位置的差值)小于50%通信距离的已定位节点占网络中所有节点的比例．

(2)平均定位误差：定位误差小于0.05的节点平均位置误差与通信距离的比值．

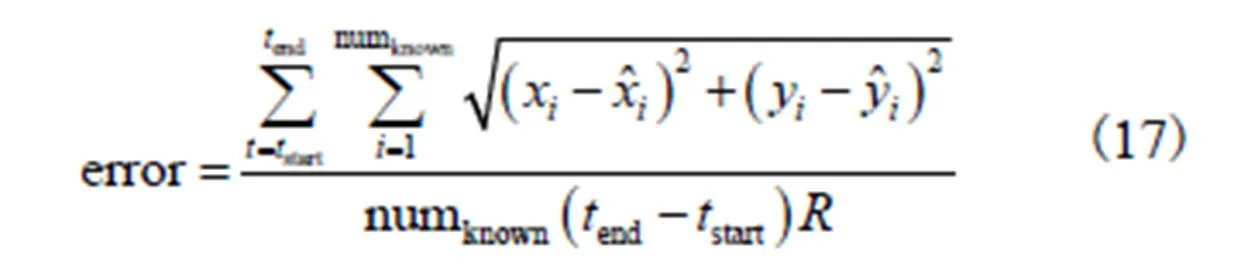
(3)平均通信能耗：节点发送的数据包格式相同，假设不考虑数据包的大小，定义平均通信能耗为平均每秒每个节点交换信息的次数．

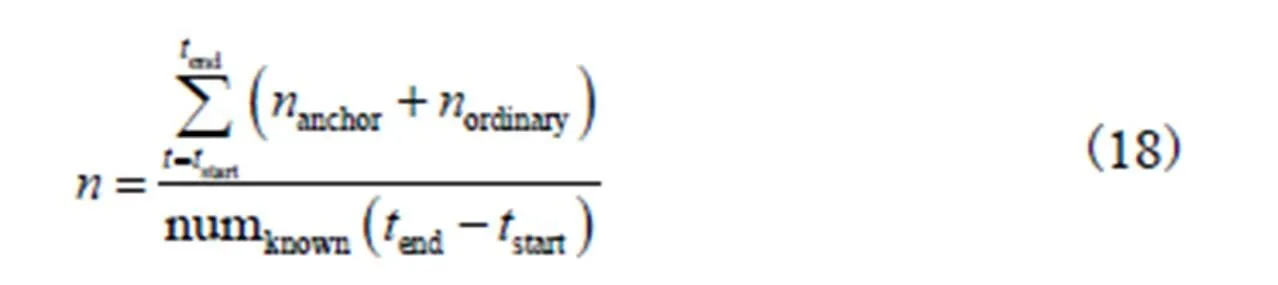
3.3 仿真结果分析

3.3.1 节点通信半径对定位覆盖度的影响

定位覆盖度是衡量定位算法适应性的重要指标．算法的定位覆盖度越高，其适应性越强．在锚节点分布确定的水下传感器网络中，节点的通信半径越大，网络的定位覆盖度越高，如图4所示．在节点通信半径或者锚节点比例相同时，SLMP算法依赖锚节点速度的AR模型来实现预测定位，HPLM-AK算法在锚节点速度AR模型的基础上加入了Kalman滤波机制来进行预测，提高了算法在水下传感器网络系统中的抗干扰能力，使得锚节点的定位精度得到了提高，普通节点根据锚节点的速度信息和位置信息来实现定位，因此普通节点的位置精度增加，从而实现定位的节点数量增加．故HPLM-AK算法的定位覆盖度要明显优于SLMP算法．

3.3.2 节点通信半径对平均定位误差的影响

平均定位误差是衡量节点定位精度的重要性能指标．算法的平均定位误差越小，其应用范围越广．节点通信半径的增加提高了邻居参考节点数量，普通节点选择置信度较高的参考节点来参与自身定位过程，定位误差减小，如图5所示．在节点通信半径或锚节点比例相同时，HPLM-AK算法的平均定位误差小于SLMP算法．两种算法中，平均定位误差都是由锚节点定位误差和普通节点定位误差组成的．SLMP算法中普通节点的累积误差完全依赖于锚节点速度的预测精度．在HPLM-AK算法中，对锚节点速度预测时考虑到噪声的干扰，利用卡尔曼滤波方法对锚节点的速度信息做出最优估计，提高了锚节点的速度和位置精度；同时参考节点信息列表更新机制提高了参考节点信息的准确性和实时性，降低了普通节点的定位误差．

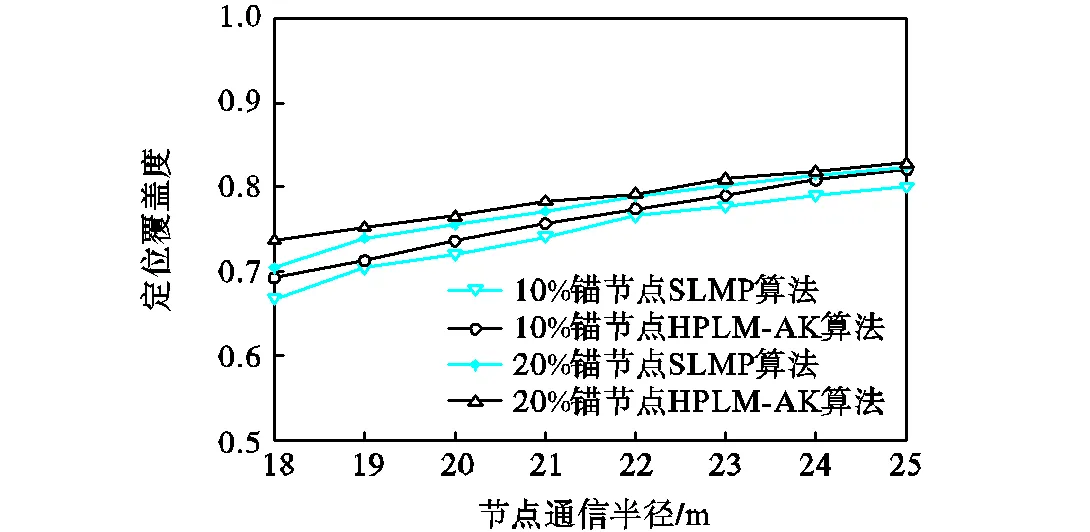
图4 定位覆盖度与节点通信半径的关系

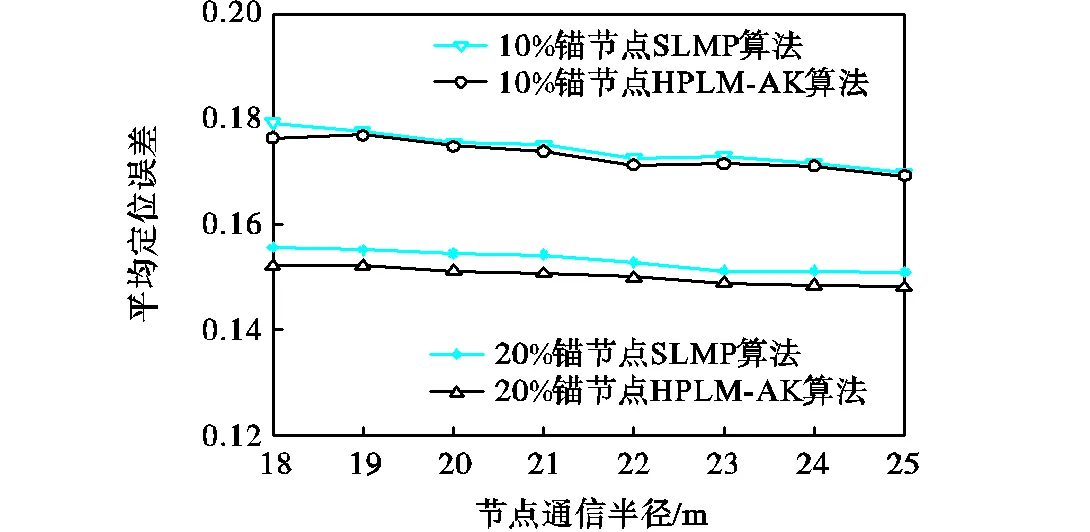
图5 平均定位误差与节点通信半径的关系

3.3.3 节点通信半径对平均通信能耗的影响

水下传感器节点的能量受限，因此降低传感器网络的通信能耗也是节点定位方法重要的衡量指标．算法的平均通信能耗越低，其网络寿命越长．节点通信半径的增加使得普通节点的邻居参考节点数量增加，则节点间通信次数增加，进而通信能耗增加，如图6所示．在节点通信半径或锚节点比例相同时，HPLM-AK算法的平均通信能耗小于SLMP算法．在HPLM-AK算法中，基于AR模型利用卡尔曼滤波算法对锚节点的速度信息做出了最优估计，相比SLMP算法中锚节点的运动模型更为精确，使用时间长，降低了锚节点运动信息的更新频率，从而降低了通信能耗．

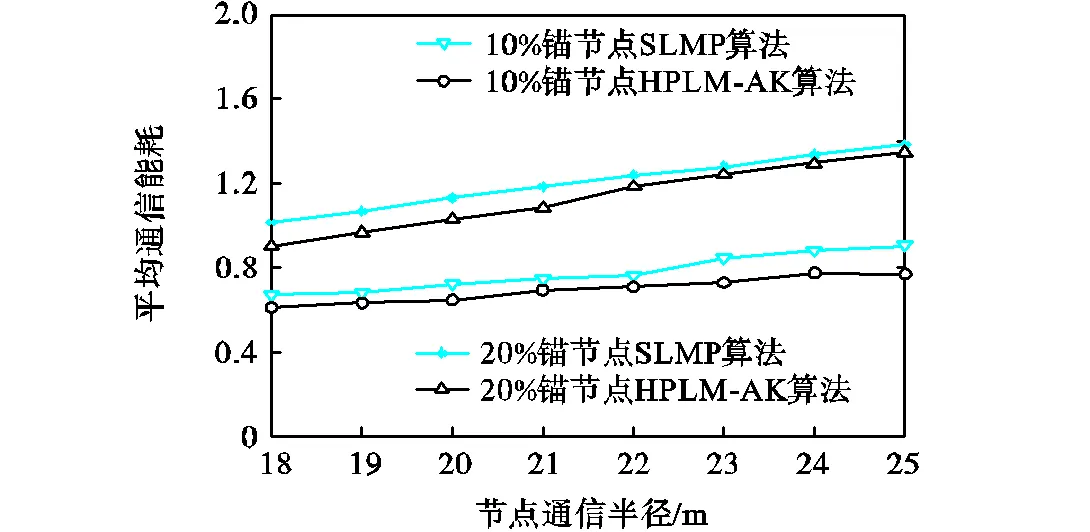
图6 平均通信能耗与节点通信半径的关系

4 结 语

本文针对水下无线传感器网络节点移动性强、拓扑变化频繁的特点，提出了基于AR模型和卡尔曼滤波的UWSNs节点分层预测定位算法．利用AR模型和卡尔曼滤波算法建立了锚节点的预测定位算法，锚节点能够与信标节点直接通信更新锚节点的运动预测模型，在保证节点预测定位精度的同时，有效减少了网络的能量消耗．普通节点利用邻居参考节点的运动信息，来建立自身的运动模型进行预测定位，通过更新参考节点列表机制选择精度较高的参考节点来辅助自身定位，提高了节点的定位精度．对E117.25°～E132.20°和N24.00°～N43.45°海域数据仿真分析结果表明：HPLM-AK算法性能优于SLMP算法，HPLM-AK算法的定位覆盖度更高，平均定位误差更小，平均通信能耗更低．

［1］ Akyildiz L F，Pompili D，Melodia T. Underwater acoustic sensor networks：Research challenges[J]. Ad Hoc Networks，2005，3(3)：257-279.

［2］ Chandrasekhar W，Seah W. An area localization scheme for underwater sensor networks[C]// IEEE Oceans 2006-Asia Pacific．Singapore，2006：911-918.

［3］ Mirza D，Schurgers C. Motion-aware self-localization for underwater networks[C]// Proceedings of the 3rd International Workshop on Underwater Networks．San Francisco，CA，USA，2008：51-58.

［4］ Cheng W，Thaeler A，Cheng X Z，et al. Time-synchronization free localization in large scale underwater acoustic sensor networks[C]// 29th IEEE International Conference on Distributed Computing Systems Workshops(ICDCS Workshops)．Montreal，QC，Can-ada，2009：80-87.

［5］ Zhang Y，Liang J X，Jiang S M，et al. A localization methods for underwater wireless sensor networks based on mobility prediction and particle swarm optimization algorithms[J]. Sensors，2016，16(2)：1-17.

［6］ Zhou Z，Peng Z，Cui J H，et al. Scalable localization with mobility prediction for underwater sensor networks[J]. IEEE Transactions on Mobile Computing，2011，10(3)：335-348.

［7］ Marshall J，Adcroft A，Hill C，et al. A finite-volume，incompressible Navier Stokes model for studies of the ocean on parallel computers[J]. Journal of Geophysical Research，1997，102(C3)：5753-5766.

［8］ Beerens S P，Ridderinkhof H，Zimmerman J T F. An analytical study of chaotic stirring in tidal areas[J]. Chaos，Solitons and Fractals，1994，4(6)：1011-1029.

［9］ Bagtzoglou A C，Novikov A. Chaotic behavior and pollution dispersion characteristics in engineered tidal embayments：A numerical investigation[J]. Jawra Journal of the American Water Resources Association，2007，43(1)：207-219.

［10］ 黄小平，王 岩. 卡尔曼滤波原理及应用[M]. 1版. 北京：电子工业大学出版社，2015.Huang Xiaoping，Wang Yan. Principle and Application of Kalman Filter[M]. 1st ed. Beijing：Publishing House of Electronics Industry，2015(in Chinese).

［11］ Schroeder M R. Linear Prediction Theory：A Mathematical Basis for Adaptive Systems[M]. Berlin：Springer-Verlag，1989.

Hierarchical Prediction Localization Method Based on AR Model and Kalman for Underwater Wireless Sensor Networks

Liu Liping，Cao Liusheng，Chen Meng

(School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China)

Underwater wireless sensor networks(UWSNs) have frequent topology changes and limited communication capabilities，which pose great challenges to localization in underwater environment monitoring network. In seashore monitoring networks，considering that node mobility pattern shows certain semi-periodic property，a hierarchical prediction localization method based on AR model and Kalman algorithm(HPLM-AK)is proposed for UWSNs. Considering the requirements of network energy consumption and localization accuracy，the state equation and the observation equation of anchor node velocity based on AR prediction model are established. Kalman algorithm is used to estimate the optimal anchor node velocity information to improve the localization accuracy and reduce communication cost. According to the spatial correlation between ordinary nodes and anchor nodes，the speed and the position information of anchor nodes are used to locate ordinary nodes. To improve the localization coverage，the localization confidence value is designed to upgrade ordinary nodes to reference nodes to compensate for the sparseness of anchor node. Moreover，an update mechanism of the reference node list，which can update the information of reference nodes in time is designed to improve the accuracy of ordinary nodes localization. The simulation results based on ocean data in the region from E117.25° to E132.20° and from N24.00° to N43.45° show that the HPLM-AK method has higher localization coverage and lower localization error and communication cost than the scalable localization with mobility pattern(SLMP)method.

underwater wireless sensor networks；AR model；Kalman filter；reference list；hierarchical prediction localization

TP393

A

0493-2137(2019)01-0098-07

2018-06-05；

2018-09-09.

刘丽萍（1979—  ），女，博士，副教授.

刘丽萍，lipingliu@tju.edu.cn.

国家自然科学基金资助项目(61104208).

the National Natural Science Foundation of China(No. 61104208).

10.11784/tdxbz201806006

(责任编辑：孙立华)