基于级联过完备字典稀疏表征的滚动轴承复合故障诊断方法

郑 胜， 刘 韬， 刘 畅， 李 华

(昆明理工大学 机电工程学院，昆明 650500)

滚动轴承是旋转机械的重要组成部分，同时也是最容易损坏的组件。统计显示，在使用滚动轴承的旋转机械中，约有30%的机械故障都与轴承相关，其运行状态直接影响着设备的整体性能。在实际的工业环境中，考虑到成本等相关因素，机械设备通常在受到一定程度的损坏后才进行检修和零部件更换。此时机械设备中的轴承往往不再是一种故障，而是多种故障耦合在一起。与单一故障相比，复合故障中的多个故障相互干扰，对机械设备的危害更大，诊断难度也更大[1]。因此，对滚动轴承复合故障的诊断是一个极为重要的研究领域。

稀疏理论最早由Olshausen[2]提出，并随着不断地发展和深入，逐渐成为声音与图像处理[3-5]、压缩感知[6-7]和信号处理[8]等方向的研究热点。Du等[9]提出了一种根据齿轮和滚动轴承故障冲击形态特征的不同，进而构造不同的冗余字典并与稀疏表征算法相结合，以实现齿轮和滚动轴承复合故障的分离。唐承志[10]通过使用不同种类的原子库联合构建级联原子库对多种信号进行稀疏分解实现了不同类信号的稀疏表示。陈向民等[11]基于共振稀疏分解方法和信号各成分品质因子差异，将轴承故障信号分解成高共振分量、低共振分量和残余分量，进而包络解调低共振分量，提取了故障特征频率。而 K-SVD(K-singular value decomposition)自适应冗余字典[12]、相关滤波法Laplace小波原子优选构造过完备字典[13]等分别与正交匹配追踪(orthogonal matching pursuit，OMP)、FFT(fast fourier transform)进行改进的匹配追踪算法结合，实现了滚动轴承的故障特征提取。文献[14]基于改进自适应无参数小波变换(improved adaptive parameterless empirical wavelet transform，IAPEWT)和自适应稀疏编码收缩去噪(adaptive sparse coding shrinkage denoising，ASCSD)对故障轴承的信号进行自适应稀疏去噪，增故障强脉冲特征，有效识别了轴承故障。He等[15]以轴承阻尼二阶系统的冲击响应函数构建过完备原子库，通过相关滤波法从故障信号中识别出系统固有频率和相对阻尼比，降低字典的冗余性；并在此基础上，通过匹配追踪算法对轴承故障信号分段进行匹配，以提高在低信噪比下信号重建的效率和精度。Tang等[16]提出一种基于移不变稀疏编码算法以实现对早期微弱故障的特征提取，并通过轴承和齿轮的振动信号进行验证，取得较好的效果。

国内外学者将稀疏表征理论运用于对滚动轴承的故障诊断，并取得了很好的成效，但大多是对单一故障的诊断，较少是对复合故障的诊断。本文旨在通过级联过完备字典与以基追踪降噪问题为优化原则的特征符号搜索算法来实现对滚动轴承复合故障的分离和特征提取。文中首先简述了基于特征符号搜索算法求解基追踪降噪约束问题的基础理论，给出了确定字典情况下最优稀疏系数求解方法。然后，叙述基于相关滤波构建级联过完备字典的方法，同时给出所提复合故障诊断方法的实现过程和流程图。最后对方法的有效性通过仿真和实验信号进行验证并给出结论。

1 稀疏优化算法

信号的稀疏表征旨在冗余的原子字典里寻找最稀疏的表达方式，即用最少的原子来表示信号，从而实现对信号本质的捕捉表达[17]。Chen等[18]提出的基追踪算法使用l1范数作为稀疏系数s的稀疏性度量函数，可得到全局最优解，其优化目标函数以矩阵形式表示为

min‖s‖1， s.t.x=As

(1)

式中：基函数矩阵A=[a1,a2,…,ai]；稀疏系数矩阵s=[s1,s2,…,si]T。信号含噪声时，其模型可表示为

y=x+σz

(2)

式中：σ为噪声方差，表示噪声强度；z为噪声；y为含噪声信号；x为无噪声信号。为了从y中恢复出x的信息，基追踪降噪问题等同于求解下列约束问题[19]

(3)

式中，s与参数λ相关，它将原始信号可以分解为重构部分和残余部分

y=x+r

(4)

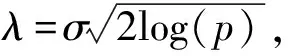
当基函数A确定时，式(3)的求解等同于求解l1范数正则化最小二乘问题，本文采用特征符号搜索算法[21]来求解此问题。如果我们知道在取得最优解时每个稀疏系数的符号(正号、负号或零)，此时‖s‖1中的l1范数便可无需考虑。若只考虑非零系数，便可将其简化为一个标准的无约束二次优化问题，从而实现高效求解。然后根据求解后稀疏系数的符号和假定符号的异同来更新系数。算法基本流程如下:

步骤2在值为零的系数si中搜索i=arg maxi|∂‖y-As‖2/∂si|，并将满足下述条件的i并入到active set集合中。

(a)若∂‖y-As‖2/∂si>λ，则θi=-1；

(b)若∂‖y-As‖2/∂si>-λ，则θi=1。

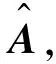
(5)

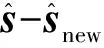
步骤4查看最优条件

(a)若∀si≠0，都有∂‖y-As‖2/∂si+λsign(si)=0，都有成立，则查看条件(b)，否则返回步骤3；

(b)若∀si=0，都有成立|∂‖y-As‖2/∂si|≤λ，则输出系数s，否则返回步骤2。

2 级联过完备字典构建与轴承复合故障诊断

2.1 基于相关滤波构建级联过完备字典

除了稀疏求解算法，稀疏字典的选取和构建也极大影响着稀疏表示效果，字典原子越符合信号的特征，就越有利于实现信号的稀疏表征。一般而言，字典存在两种类型：①由数学模型来表示的分析字典，如Gabor字典、余弦字典、Dirac字典、Fourier字典、Laplace小波字典等；②通过训练算法识别信号本身特点而学习得到的学习字典。分析字典在信号稀疏表示上具有精度高、不易受噪声干扰的特点，本文选用分析字典构建级联过完备字典。

通过分析点蚀或剥落故障轴承的旋转动力学模型及其加速度振动信号时域特征，本文选用轴承阻尼二阶系统的单位冲击响应函数构建稀疏字典，该基函数与轴承点蚀剥落故障信号匹配度高，其定义为

t∈[u,u+ws]

(6)

式中：r={fn,ξ,u}为参数矢量，fn为故障冲击激发的系统共振频率，ξ∈[0,1)为黏滞阻尼比，表示冲击响应的阻尼衰减特性，u为时移参数；ws为基函数支撑区间宽度。某参数值下字典原子波形如图1所示。

图1 字典原子波形Fig. 1 Dictionary atomic waveform

本文以存在两种故障信号为例，构建级联过完备字典。假设复合信号x(t)=x1(t)+x2(t)+n(t)，其中x1(t),x2(t)为故障信号，n(t)为噪声信号。参数(fn,ξ,u)的取值对稀疏分解的结果有着极为重要的影响，这里我们采用相关滤波法(correlation filtering，CF)[22]来识别故障冲击信号波形的频率、阻尼比，并择最优作为原子的形态参数fn，ξ，时移参数u取值采样频率的倒数。通过相关滤波可得到信号x(t)与基原子ψr(t)的相关系数曲线，分析曲线上的峰值点，可分别得到与信号x1(t)和x2(t)相关性最佳的原子，并取其对应的频率和阻尼比值，即(fn1,ξ1)和(fn2,ξ2)。将得到的最佳原子形态参数值代入式(6)中，并通过不同的时移参数张成级联过完备字典A，其表达式为

(7)

2.2 轴承复合故障诊断方法

滚动轴承发生复合故障时，其故障冲击可能会激起多个共振带或同处一个共振带内，对此需对振动信号频谱作分析，确定其共振频带带宽和个数，以减少搜寻范围，增强相关滤波的计算效率。为便于区分和提取参数，可针对不同频带分开绘制相关系数曲线图。本文提出的基于级联过完备字典与特征符号搜索算法的滚动轴承复合故障诊断方法实现步骤如下：

步骤1对采集到的故障振动信号去均值、分析频谱，确定其共振频带带宽；

步骤2根据步骤1确定的频带带宽确定共振频率fn集合F，选取SNR较高的一段信号进行相关滤波，根据所选信号时长指定参数u的集合T，根据信号衰减特性指定阻尼比ξ的集合Z；

步骤3基于相关滤波得到信号x(t)中不同故障信号最佳相关原子，取对应的频率和阻尼比值，并结合时移参数构建级联过完备字典A；

步骤4将构建的级联过完备字典A代入特征符号搜索算法中，计算信号在级联过完备字典中的最优稀疏系数s；

步骤5将最优稀疏系数结合对应的字典原子分别进行稀疏重构，得到分离后的不同故障信号，如式(8)所示，实现轴承复合故障信号的分离和降噪。

x(t)=x1(t)+x2(t)+n(t)=A1s1+A2s2+n(t)

(8)

步骤6对降噪重构后的信号进行希尔伯特包络谱分析(envelope spectrum analysis，ESA)，提取轴承复合故障的各故障特征频率，原始信号的残余部分可认为是噪声干扰成分。算法流程图如图2所示。

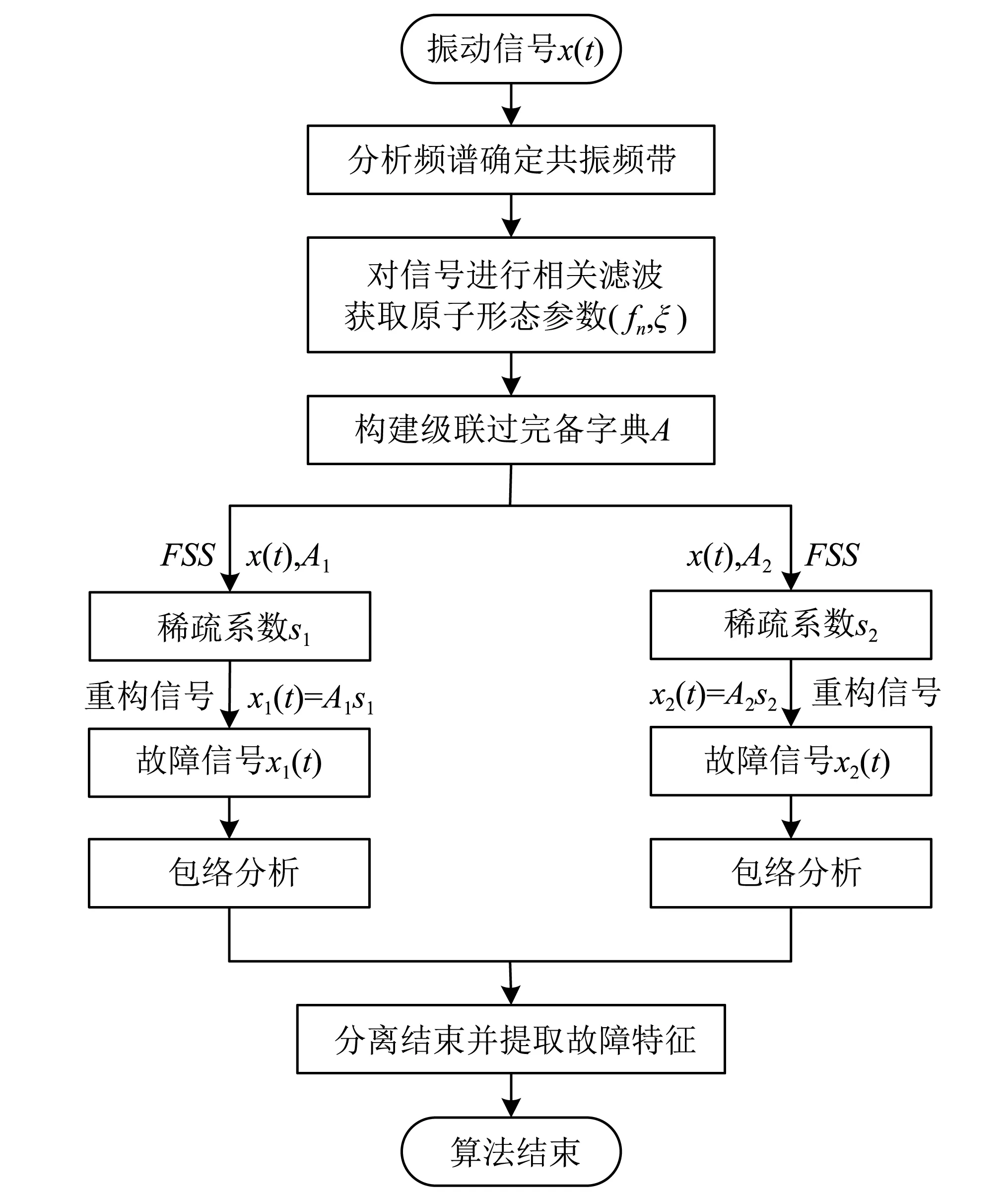
图2 轴承复合故障诊断算法流程图Fig.2 Flow chart of bearing compound faults diagnosis algorithm

3 仿真与实验验证

3.1 仿真验证

根据滚动轴承在内圈、外圈和滚动体上发生剥落故障时的特点构造故障仿真信号x(t)，其表达式[23-24]

(9)

且

(10)

式中：Ai为周期为1/Q的调制幅值；Q为旋转周期(转频fr=1/Q)；CA为幅值随机常数(CA>A0)；s(t)为点蚀故障引起的冲击；T为冲击周期；ξ为黏滞阻尼比；fn为系统的共振频率；随机变量τi为第i次冲击相对于平均周期T的微小滑动；n(t)为随机噪声。

设置内圈故障仿真信号xi(t)参数为：幅值Ai=2，采样频率fs为25 600 Hz，内圈故障共振频率fn为4 000 Hz，故障特征频率fp=54 Hz。设置外圈故障仿真信号xo(t)参数为：幅值Ao=2，采样频率fs同样为25 600 Hz，外圈故障共振频率fn为2 000 Hz，故障特征频率fp=36 Hz。轴承的转速设为600 r/min(fr=10 Hz)，将内外圈仿真信号叠加构成复合故障信号，并加入信噪比为-5 dB的加性高斯白噪声n(t)。轴承内外圈仿真故障信号及复合故障信号，如图3所示。

ws=round(fs/fp)

(11)

式中：fs为采样频率；fp为轴承故障特征频率。

将构建的级联过完备字典代入稀疏优化算法中，对原始复合故障信号进行稀疏分解，分离和重构不同脉冲响应的信号，即内外圈故障信号。观察图5所示重构后的内外圈故障信号时域波形图，其基本去除了噪声，同时故障信号得到了较好提取。对稀疏重构信号进行Hilbert解调可得各自的包络谱，如图6所示，可见故障特征明显易分辨，噪声得到了很好的抑制。

图3 内外圈故障及其复合故障仿真时域波形Fig.3 Time domain waveform of inner and outer loop fault and its compound fault simulation

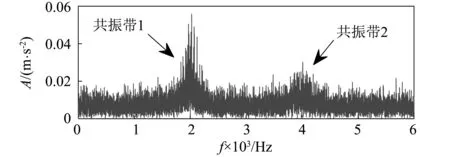
图4 复合故障仿真信号频谱图Fig.4 Spectrum of composite fault simulation signal

从上述仿真分析结果可知，基于级联过完备字典与特征符号搜索算法可有效地将含噪的复合故障信号进行分离和降噪，稀疏重构的内外圈故障信号的包络谱也可十分清晰的看到其各自的故障特征频率以及倍频、边频分量，且无相互干扰的频率成分存在。表明本文所提方法可将含噪轴承复合故障仿真信号中的内、外圈故障信号高效准确地逐一分离提取出来，现通过实验信号对其有效性进行进一步验证。

图5 复合故障仿真信号的分离与重构Fig.5 Separation and reconstruction of composite fault simulation signal

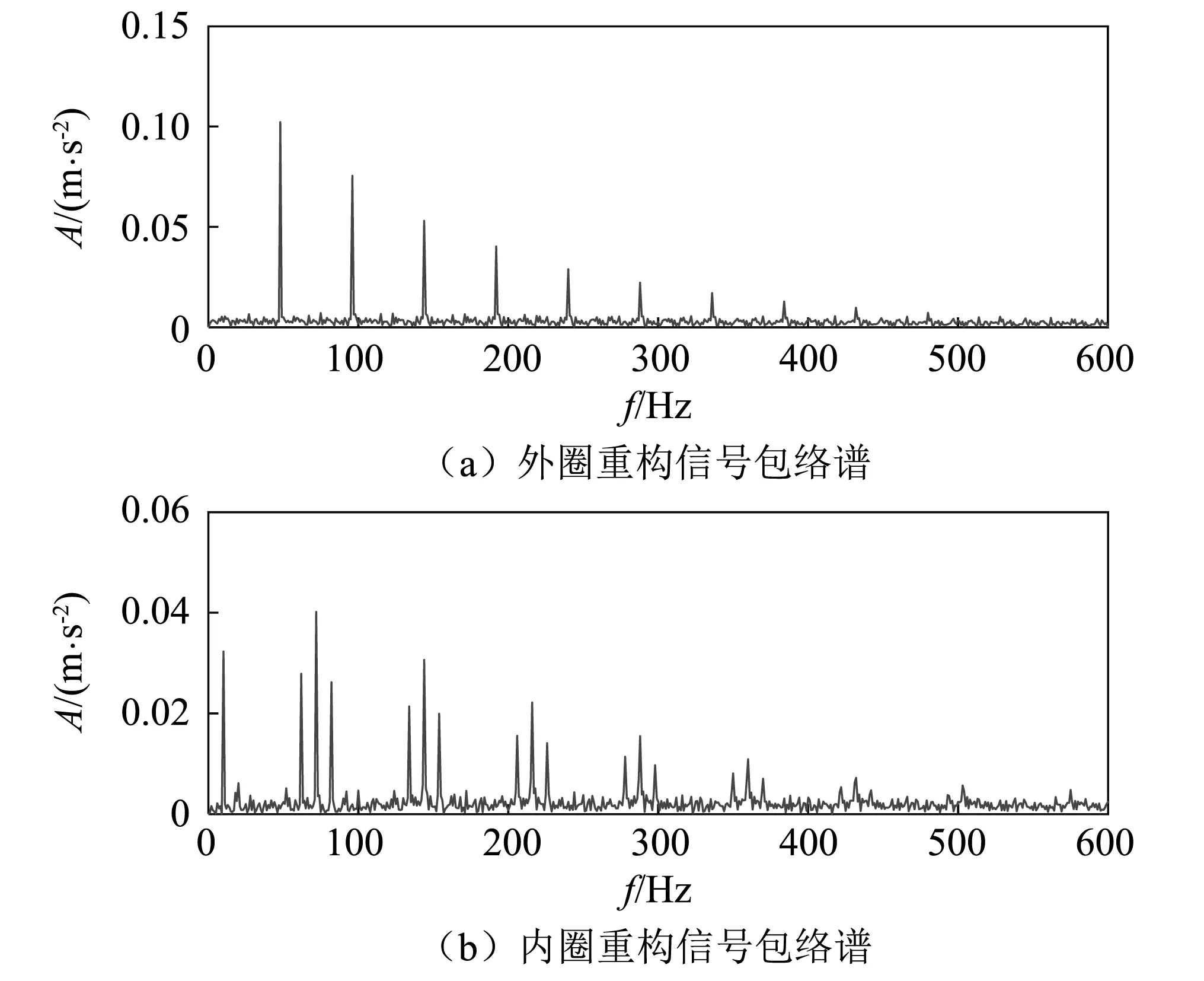
图6 复合故障仿真信号的特征提取Fig. 6 Feature extraction of composite fault simulation signal

3.2 实验验证

实验验证数据为滚动轴承疲劳寿命实验采集得到。实验设备采用杭州轴承试验研究中心有限公司ABLT-1A轴承寿命试验机，结构如图7所示，实验对象为NSK公司6205深沟球轴承。转轴转速为3 000 r/min (转频fr=50 Hz)，采样频率为51 200 Hz，从实验起始到轴承失效共持续了269 h，均方根RMS达到21 mm/s，此时轴承完全失效，拆解实验轴承发现其内圈和外圈皆发生点蚀剥落故障。NSK6205深沟球轴承内外圈理论故障特征频率为：外圈fo=181.73 Hz，内圈fi=268.27 Hz。NSK6205轴承故障区放大图如图8、图9所示。

选取发生故障后某一时刻的全寿命数据，其时域波形如图10所示，同时绘制其频谱、包络谱如图11、图12所示。

图7 ABLT-1A轴承寿命试验机Fig.7 ABLT-1A bearing life testing machine

图8 6205轴承内圈故障拆解图Fig.8 6205 disassembly drawing of bearing inner ring fault

图9 6205轴承外圈故障拆解图Fig.9 6205 disassembly drawing of bearing outer ring fault

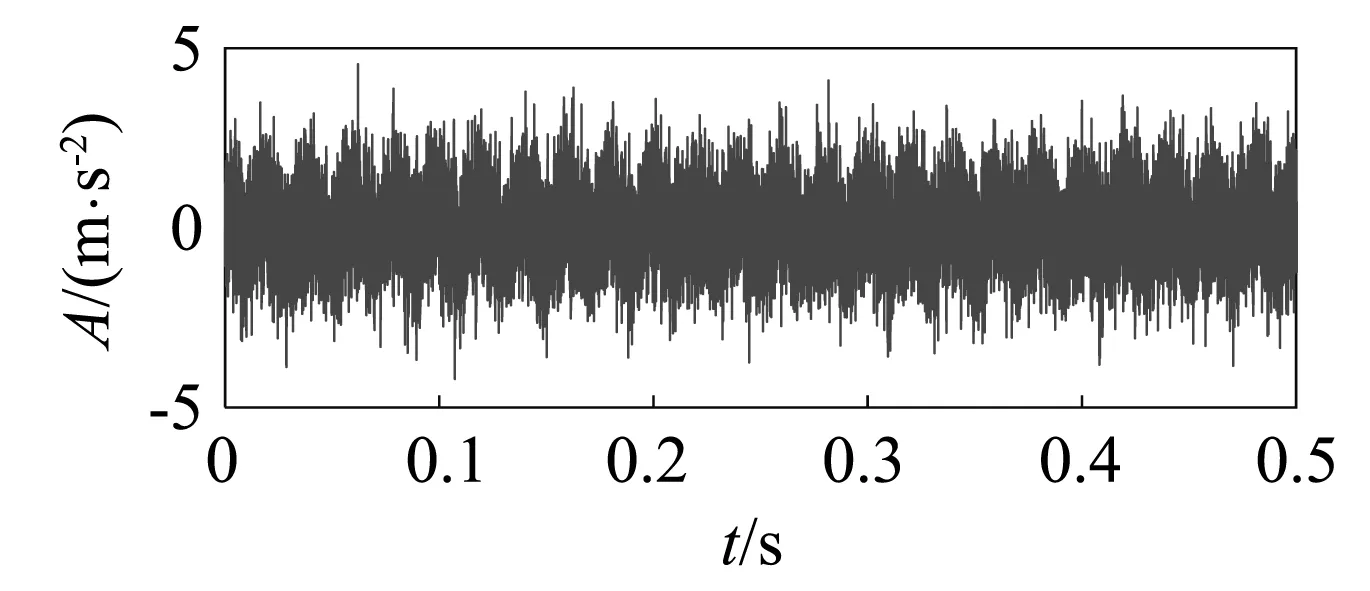
图10 复合故障信号时域波形Fig.10 Time domain waveform of composite fault signal

图11 复合故障信号频谱图Fig.11 Spectrum of composite fault signal

图12 复合故障信号包络谱图Fig.12 Envelope spectrum of composite fault signal

图13 外圈重构信号时域波形图Fig.13 Time domain waveform of outer circle reconstruction signal

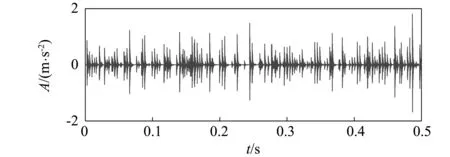
图14 内圈重构信号时域波形图Fig.14 Time domain waveform of inner circle reconstruction signal

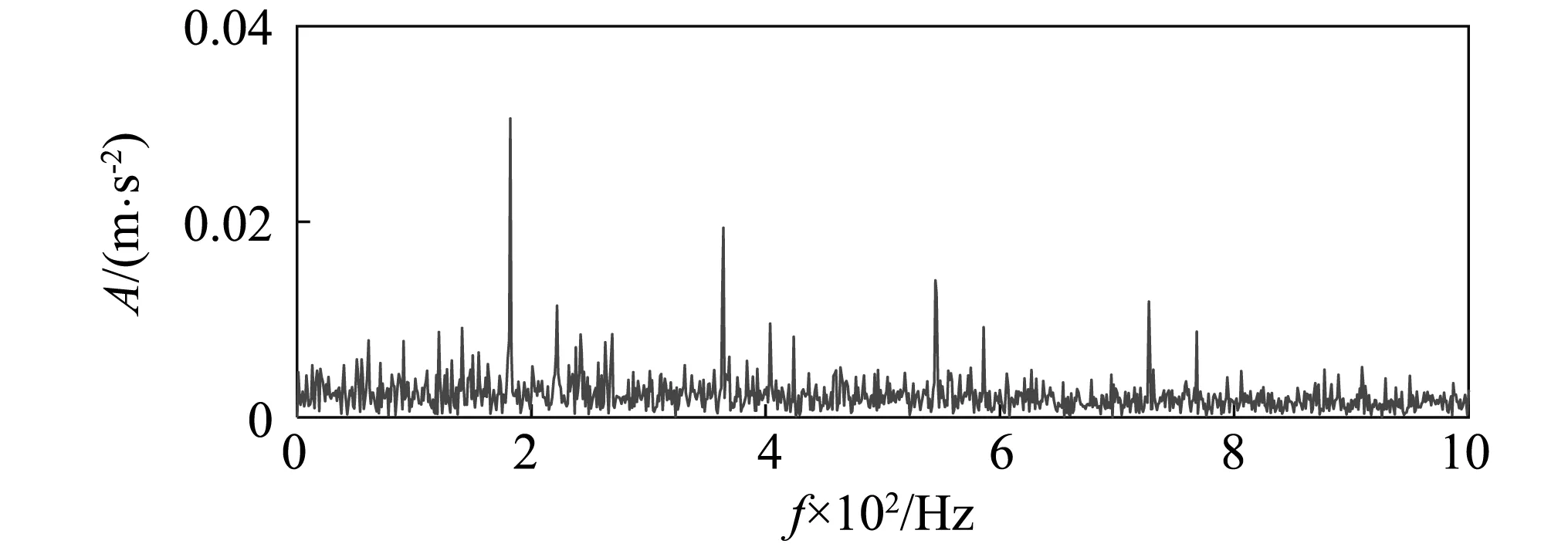
图15 外圈重构信号包络谱Fig.15 Envelope spectrum of outer circle reconstruction signal

图16 内圈重构信号包络谱Fig.16 Envelope spectrum of inner circle reconstruction signal

从全寿命实验数据分析结果可知，基于级联过完备字典与特征符号搜索算法同样可准确有效地分离实测复合故障信号。分离后的信号包络谱表明，该方法很好的提取到了各故障的特征频率以及倍频、边带成分，且相互间干扰的频率很小，谱图也较为干净。从重构的故障信号图和各自的包络谱可看出，其实现了很好的降噪，故障特征频率易识别。对此实验验证了本文所提方法在轴承复合故障分离和特征提取方面具有可行性与有效性。

4 结 论

本文利用相关滤波来估算构建与轴承点蚀剥落故障信号相匹配的级联过完备字典的参数，然后将构建的级联字典与以基追踪降噪问题为优化原则的特征符号搜索算法相结合，进而实现对轴承复合故障的分离和特征提取。仿真和实验验证表明，本文所述稀疏优化算法可高效求解信号在级联过完备字典上的最优稀疏表示系数，且通过稀疏系数结合对应的字典原子可有效地实现对信号的分离和重构，并达到信号降噪的目的。对分离重构后的信号进行包络分析，其可清晰准确地提取到各类故障的特征频率。