轴对称结构动力弹塑性分析的无网格自然邻接点Petrov-Galerkin法
陈莘莘, 肖树聪, 周书涛
(1.华东交通大学 土木工程国家实验教学示范中心,南昌 330013;2. 北京强度环境研究所,北京 100076)
作为近年来兴起的一种新的数值方法,无网格法[1-3]可以克服有限元等传统数值方法对网格的依赖性,在很大程度上缓解了网格扭曲导致的数值困难。目前,一系列的无网格法相继被提出,如:无单元Galerkin法[4-5]、无网格局部Petrov-Galerkin法[6- 7]、边界无单元法[8-9]、自然单元法[10-11]和杂交边界点法[12-13]等。与大多数无网格方法不同,无网格局部Petrov-Galerkin(meshless local Petrov-Galerkin, MLPG)法是基于微分方程的局部弱形式,进行积分计算时只需要布置局部的积分单元,被誉为是一种真正的无网格法。然而,基于移动最小二乘近似的MLPG方法不能直接施加本质边界条件。为了克服这一困难,Cai等[14-15]提出的无网格自然邻接点Petrov-Galerkin法不仅允许权函数和试函数取自不同的函数空间,而且以节点的真实变量作为未知函数,从而可以直接施加本质边界条件。在这种无网格法中,任意节点的子域可由以该节点为公共顶点的Delaunay三角形构成的多边形区域,且积分可转化为构成该子域的Delaunay三角形区域上的积分之和。此外,线性有限元形函数作为权函数可以减少被积函数的阶次,因而具有计算高效的特点。鉴于这些优良特性,近年来无网格自然邻接点Petrov-Galerkin法的在很多领域均得到了广泛的应用[16-19]。
轴对称问题在工程中非常常见,其几何形状、约束条件及作用的载荷都对称于某一固定轴。 若利用其轴对称特点,可将其转化为二维问题求解,进而减少未知量。近年来,陈莘莘等[19-20]都致力于无网格法求解复杂轴对称问题的研究,并相继取得了一些进展。其中,陈莘莘等采用无网格自然邻接点Petrov-Galerkin法求解了轴对称弹性动力学问题。然而,在结构的动力响应过程中,通常总是既有弹性变形,又有塑性变形,而且这两种变形以及它们之间的分界面都随时间变化[21]。因此,本文在采用自然邻接点插值构造径向位移和轴向位移近似函数的基础上,采用局部Petrov-Galerkin法在多边形子域上推导轴对称结构动力弹塑性分析的离散方程,并采用预校正形式的Newmark法进行迭代求解。最后,数值算例验证了本文建立的轴对称结构动力弹塑性分析方法的有效性。
1 控制方程
对于轴对称结构,通常采用圆柱坐标系(r,θ,z),以对称轴作为z轴,所有应力、应变和位移都与θ无关。任一点的位移只有两个方向的分量,即沿r方向的径向位移ur和沿z方向的轴向位移uz。在轴对称面Ω上,Γu和Γt分别为问题域的本质边界和自然边界。如果不考虑阻尼,轴对称结构动力弹塑性问题的平衡方程可写为
(1)
(2)

(3a)
(3b)
ui(x,t)|t=0=ui(x,0)
(4a)
(4b)

材料进入塑性状态后,继续加载时的应力应变关系为
dσ=Depdε
(5)
式中:dσ和dε分别为应力增量和应变增量;Dep为弹塑性矩阵,且有
(6)
(7)
Dep=De-Dp
(8)
式中,De和Dp分别为弹性矩阵和塑性矩阵,且有
(9)
式中:σs为屈服应力;G和Ep分别为剪切模量和塑性模量;sr,sz和sθ为应力偏量。
2 动力弹塑性问题的离散化实现
2.1 自然邻接点插值
对轴对称面Ω上的任一节点x1,其一阶Voronoi结构TI可定义为
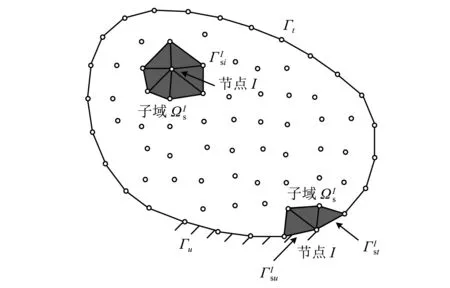
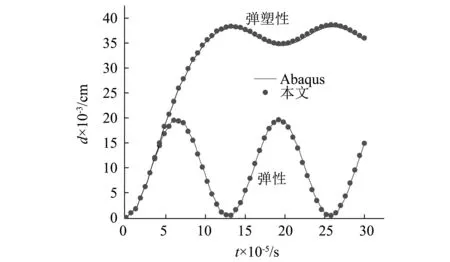
TI={x∈R2∶d(x,xI) (10) 式中,d(x,x1)为点x和xI之间的距离。显然,TI为以节点xI为最近离散点的空间点位置的集合。 为了对某点进行插值,还需要引入插值点的二阶Voronoi结构TIJ,其数学表达式为 TIJ={x∈R2∶d(x,xI) (11) 实际上,TIJ是以节点xI为最近点,节点xJ为第二近点的空间点位置的集合。图1所示为平面中7个节点的Voronoi结构以及插值点x的二阶Voronoi结构。 图1 点x的一阶和二阶Voronoi结构Fig.1 First-order and second-order Voronoi cell about x 设AI(x)和A(x)分别为插值点x的二阶Voronoi结构TxI和一阶Voronoi结构Tx的面积,则自然邻接点形函数及其导数可以表达为 φI(x)=AI(x)/A(x) (12) φI,j(x)=(AI,j(x)-φI(x)AI,j(x))/A(x) (13) 定义了各节点的插值函数后,点x的位移函数可写为 (14) 式中:uI(I=1,2,…,n)为点x周围n个自然邻接点的节点位移;φI(x)为对应节点的形函数。 (15) (16) 式中,vI为加权函数。 利用格林公式对式(15)中积分的前两项进行分部积分,可得 (17) (18) 类似地,由式(16)可得 (19) 为了便于数值计算,联立式(18)和式(19)可得 (20) 其中, u=[ur,uz]T,σ=[σr,σz,σθ,τrz]T (21a) (21b) (21c) 由于只对空间域进行离散,轴对称面Ω内的位移u(x,t)可由式(14)写为 (22) 图2 局部多边形子域Fig.2 The local polygonal sub-domains 将式(22)代入式(20),可得轴对称结构动力弹塑性分析的离散控制方程为 (23) 其中, (24a) (24b) (24c) 其中, (25) 求解运动方程式(23),本文采用预校正形式的Newmark方法。采用Newton-Raphson迭代,时间t+Δt的运动方程可由式(23)改写为 (26a) t+Δtu(k+1)=t+Δtu(k)+Δu(k) (26b) 式中,KT为切线刚度矩阵。 (27) (28a) (28b) 式中,α和β为按积分精度和稳定性要求决定的参数。联立式(26b)和式(28b),得到 (29) 将式(29)代入式(26a),则可得到如下的静力等效问题 K*Δu(k)=t+Δtf(k) (30) 其中, K*=KT+M/(α(Δt)2) (31) (32) 静力等效问题式(30)的具体迭代过程可参见文献[22]。 为了验证所提数值方法的有效性,本文对轴对称结构动力弹塑性分析的一些典型算例进行计算和对比分析。如果不作特别说明,材料均取为服从Von Mises屈服条件的理想弹塑性材料。 无限长受突加内压P=185 Pa的厚壁圆筒,内半径a=100 m,外半径b=200 m,弹性模量E=2.1×105Pa,泊松比v=0.3,屈服应力σs=355 Pa,质量密度ρ=7.85×10-6kg/m3。截取一段h=100 m作为计算模型,其节点布置方案如图3所示,且时间步长取为Δt=1.0×10-5s。图4给出了厚壁圆筒内表面A点的径向位移随时间的变化曲线,图5给出了厚壁圆筒r=150 m处的弹塑性径向应力σr随时间的变化曲线。从图4和图5可以看出本文数值解与有限元软件Abaqus的计算结果吻合很好。 图3 厚壁圆筒节点布置Fig.3 Nodal distribution for the thick-walled cylinder 图4 厚壁圆筒内表面的径向位移Fig.4 Radial displacement history at the inner surface of the thick-wallled cylinder 图5 r=150 m处的弹塑性径向应力σr Fig. 5 Elastoplastic radial stress σr when r=150 m 考虑一受突加均布内压P=75 MPa的厚壁球壳,其外壁半径R1=0.2 m,内壁半径R2=0.16 m。弹性模量E=2.1×1011Pa,泊松比v=0.3,屈服应力σs=200 MPa,质量密度ρ=7.85×103kg/m3。采用如图6所示的节点布置方案,时间步长取为Δt=3.0×10-7s。图7给出了厚壁球壳内表面A点的径向位移随时间的变化曲线。显然,本文数值解与有限元软件Abaqus的计算结果吻合很好,这进一步验证了本文所提方法的有效性。 图6 厚壁球壳节点布置Fig. 6 Nodal distribution for the thick-walled spherical shell 图7 厚壁球壳内表面的径向位移Fig. 7 Radial displacement history at the inner surface of the thick-walled spherical shell 本文将无网格自然邻接点Petrov-Galerkin法进一歩推广求解轴对称结构动力弹塑性问题。在采用自然邻接点插值构造径向位移和轴向位移近似函数的基础上,采用线性有限元形函数作为权函数详细推导了轴对称结构动力弹塑性分析的无网格法。这种方法不仅有效地避免了复杂的网格划分和网格畸变的影响,而且能够方便地通过加密节点提高计算精度,有利于发展相关的自适应算法。另外,这种方法没有任何人为参数的选择问题,可以直接准确地施加本质边界条件,子域构造方式简单,计算效率高。本文的数值算例结果表明,采用无网格自然邻接点Petrov-Galerkin法求解轴对称结构动力弹塑性问题是可行的,而且具有较高的计算精度。
2.2 平衡离散方程

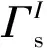
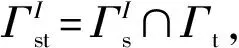

3 时间积分方案

4 数值算例
4.1 受突加内压的厚壁圆筒

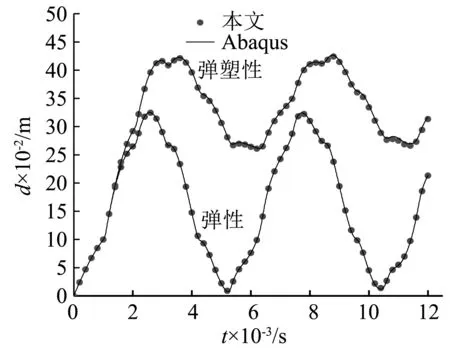

4.2 受突加内压的厚壁球壳

5 结 论

