基于非线性有限元和响应面方法的海底管道受坠物撞击损伤的风险分析

姜逢源， 董 胜， 赵玉良

(中国海洋大学 工程学院，山东 青岛 266100)

海底管道被视为近海油气产业的“生命线”，其作为连接海底设施与陆上终端的介质，承担着输送油气的重要任务，具有快捷、高效等优点。由于人类海洋活动越发频繁，平台作业和船舶抛锚等第三方活动容易对海域内的管道造成坠击损伤，从而产生油气泄露，这已成为引发管道失效事故的主要原因[1]。由于海底管道所处环境复杂，检修困难，一旦失效，将带来不可估量的经济损失和环境破坏。因此，如何确定管道正常营运状态下的可靠度，准确评估管道的失效风险是一项重要工作。

迄今，针对第三方破坏引发的海底管道失效风险已有一定的研究。有学者对于坠物落水及船舶撞击管道的概率给出了确定方法[2-3]。Bai等[4]估计了多种类型撞击下海底管道的失效概率并研究其风险预测及可接受准则。Mazzola[5]提出了一种计算海底管道受平台坠物撞击的失效概率的方法，分析了不同坠落点、管道地点对失效概率的影响。DNV[6]提出了坠物撞击下海底管道失效概率的计算方法(以下称DNV法)，该方法的提出为后续研究提供了计算框架，由于采用经验公式计算管道的损伤，忽略了诸多非线性因素的影响。Kawsar等[7]采用随机抽样法模拟了不同工况，结合有限元法求得管道失效的超越概率，但未考虑管土相互作用的影响。丁红岩等[8]和Jiang等[9]对DNV法进行了改进，引入可靠度理论求解失效概率，分析了不同坠物对管道失效概率的影响，但二者对管道失效状态的模拟均采用计算公式法，忽略了非线性因素的影响。

受海底环境荷载作用和边界条件的影响，海底管道在冲击荷载下的响应涉及到的非线性作用复杂，需通过非线性有限元分析确定其失效状态[10-11]。目前，通常采用经验公式法来描述海底管道的结构失效状态[12-13]，由于忽略了诸多非线性因素，因而无法反映结构的真实状态。海床土体作为支撑管道的介质，对冲击能力的耗散起到可观的作用[14]，目前相关分析中，对上述管-土耦合作用的考虑相对欠缺，计算得到的管道损伤较实际情况偏大，导致分析结果较为保守，造成不必要的资金投入。其中，挖沟埋深作为保障管道安全的重要手段，国内外行业规范中对于埋深的规定[15]始终没有明确标准，至今尚未建立起与失效概率与埋深的定量关系，无法有效地指导工程设计。

综上所述，目前关于管道损伤的风险分析方法对非线性作用考虑不充分，对管土耦合作用的考虑更是寥寥无几，影响工程设计与风险控制。为解决以上问题，基于Python语言的二次开发技术[16]，将非线性有限元分析法与响应面法[17]耦合，建立海底管道受坠物撞击损伤的可靠度分析模型，探讨了非线性因素及管-土耦合作用对管道失效概率的影响。本文首先介绍了可靠度分析模型的建立，其次将有限元计算结果及失效概率估计值分别与物理模型试验值及Monte Carlo法的估计值对比，验证了该模型合理性。随后从工程应用的角度，考虑管-土耦合作用因素，分析不同条件下的失效概率。最后对随机变量进行敏感性分析，得出结论。

1 非线性有限元分析

1.1 显示动力学算法

海底管道的撞击属于高速动力学问题，荷载持续时间短，量级大，结构反应变化快，涉及高度非线性因素。显式动力学算法可精确捕捉极小时间步内结构的动力响应，适用于此类问题的求解。结构的控制方程如式(1)所示，将其中的加速度项及速度项采用中心差分代替(见式(2)和式(3))，可得到相应的线性方程组(见式(4))，对其求解得到单元节点位移U后，将其代入几何及物理方程中，即可求得应力及应变。

(1)

(2)

(3)

(4)

其中，

(5)

(6)

式中：M，C，K，Rt分别为系统的质量矩阵、阻尼矩阵、刚度矩阵、荷载矩阵；Ut为单元节点位移矩阵。

1.2 耦合欧拉-拉格朗日算法

坠物侵入管道上覆土体过程中涉及高度非线性、多介质接触等问题，使土体产生极大变形，传统有限元分析方法会产生网格畸变，难以收敛。耦合欧拉-拉格朗日算法[18](coupled Eulerian-Lagrangian, CEL)是目前结构物-土体相互作用分析中的常用方法，且已嵌入有非线性限元分析程序Abaqus中。其利用欧拉网格在空间保持固定，土体材料在其中自由流动的建模方式有效解决土体大变形问题，并以欧拉体积分数EVF追踪材料的位置。同时采用拉格朗日网格去描述结构物，其应力应变响应则通过欧拉-拉格朗日接触算法获取。如图1所示，通过计算欧拉材料节点和拉格朗日节点在每一时间步内的相对位移来确定作用在二者之间的罚力，完成相互间信息的映射传递。其计算公式为

Fp=kp·dp

(7)

(8)

FE,i=NiβiFp

(9)

(10)

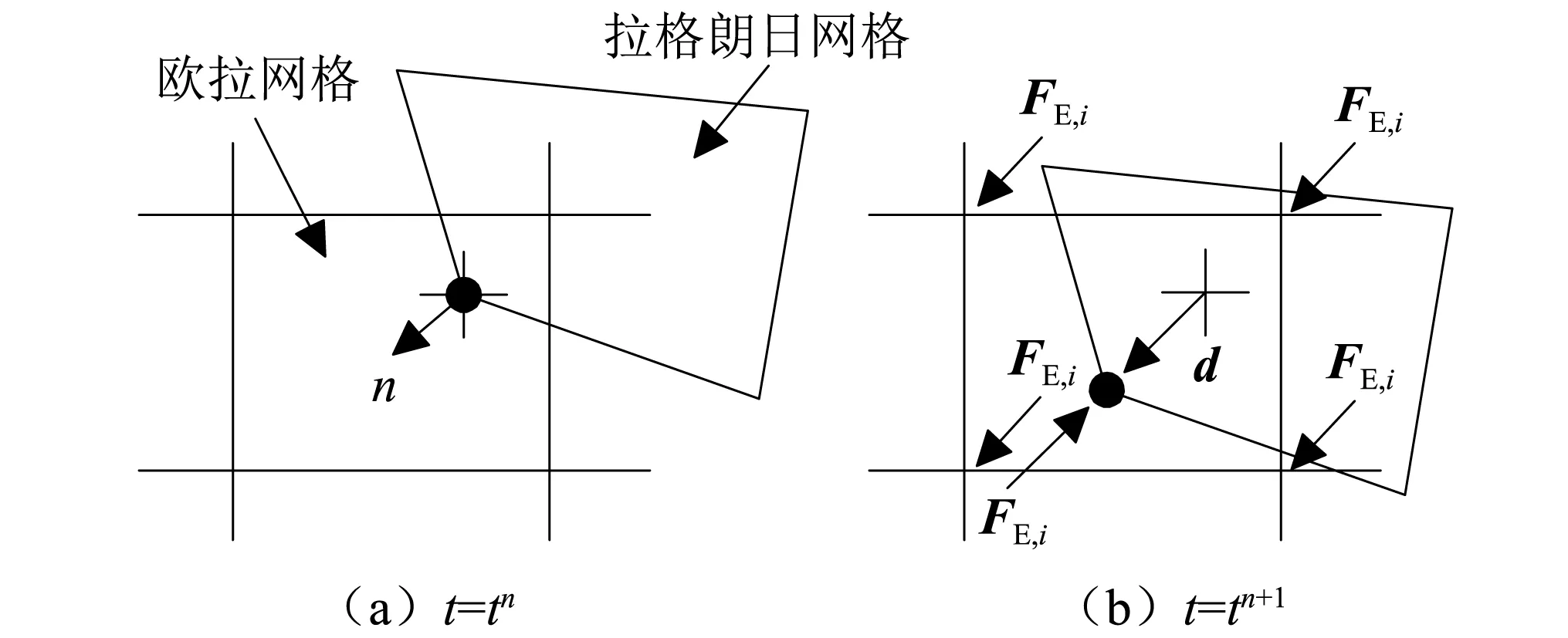
图1 耦合欧拉-拉格朗日接触算法原理Fig.1 Contact algorithm principle of CEL method

基于Abaqus平台，本文建立的有限元模型如图2所示，管道采用拉格朗日网格进行离散，其钢材料的应力应变关系使用双线性各向同性强化模型进行描述；海床土体则用欧拉网格离散，并对海床土体施加初始地应力及海水压力场，土体的弹塑形行为则用Mohr-Coulomb(MC)本构模型表示；对坠物同样采用拉格朗日网格离散，施加刚体约束及初速度，并以等效密度的方式考虑坠物的水动力因素。

注： D为管径； e为埋深。图2 坠物-管道-土体相互作用有限元模型Fig.2 Finite element model of interactions between dropped object-pipeline-soil

1.3 有限元模型验证

为验证非线性有限元模型的可靠性，选取文献[19]中船锚与埋深管道撞击的物理模型试验进行对比验证，其结果如图3所示。其中试验土样为黏土，埋深e由0～0.2 m变化。由对比结果可知，总体上数值模型与试验的结果吻合较好，平均相对误差为6.58%。但尚存在些许误差，如埋深e=0.1 m时的情况。其原因很可能是由于不同埋深管道周围土体的固结状态难以保持一致，使得土体力学特性的真实值与测量值之间存在差异，从而使得计算结果与试验结果产生偏差。由上述分析可知，本文的有限元模型可较为精确的对管道损伤进行预测。

图3 管道凹痕深度对比Fig.3 The comparison of pipeline dent depths

2 有限元-响应面耦合可靠度模型

2.1 功能函数

DNV规范中，海底管道的凹痕深度δ与管径D的比值是评估结构是否失效的重要指标，因此管道的极限状态方程可表示为式(11)，其中η为无量纲临界参数，用以控制失效判定条件，在此取η=0.2以考虑管道发生破裂造成较大危害的情况。

Z=g(x)=δ(x)/D-η

(11)

式中：x为随机变量；凹痕深度δ(·)为随机变量的函数，经有限元分析获得。

由于海底条件复杂，海底管道的制造、加工及施工过程较为复杂，难免出现一些偏差，从而影响管道的承载能力及几何尺寸，使上述因素存在变异性。故在本文的可靠度分析中，将管道钢材料的屈服强度σy、管径D及壁厚t作为随机变量来处理。上述三个随机变量均服从正态分布，均值取其标准值，变异系数依次为0.07，0.03，0.05。

2.2 实现步骤

由以上叙述可知，海底管道在冲击荷载下的损伤涉及复杂的非线性因素，结构的极限状态方程无法显式表达，传统的一次二阶矩法难以进行求解。针对极限状态方程为隐式的情况，常用的方法有：Monte-Carlo法[20]、神经网络法[21]和响应面法。但前两种方法均需大量的抽样计算，不适用于大型计算模型的求解。而响应面法仅需在结构的失效域附近进行一系列数值计算，构造出一个具有显式表达式的函数来近似结代替结构真实的极限状态曲面，从而可利用一次二阶矩法对可靠度进行求解，具有明确的收敛准则和较高的计算效率。

(12)

(13)

Python语言作为Abaqus二次开发支持的脚本语言，可用于有限元分析与响应面法的耦合，完成有限元模型的建立与更新、计算结果的提取、求解可靠度设计验算点、中心点的搜索及循环计算，使可靠度求解程序化，无需进行人为干预。表1给出了Python语言的实现流程。

表1 可靠度分析模型的Python实现

2.3 可靠度模型验证

为验证本文提出的可靠度分析模型的合理性，选取表2所列出的12种工况进行可靠度指标的计算，其中为便于对比，海床土体简化为刚性海床，坠物简化为球状刚体。将计算结果与Monte Carlo法进行对比。由于Monte Carlo法需进行大量抽样计算，考虑到时间成本及可行性，该方法中对于管道凹痕采用DNV规范推荐的公式[23]进行计算

(14)

式中：E为坠物的冲击能量；D为管道直径；t为管道壁厚；mp=1/4(σy·t2)为塑性弯矩，σy为管道钢材料屈服强度。

表2 工况设计

计算结果如图4所示，大多数计算点分布在y=x直线上部附近，这主要是由于DNV推荐的理论公式假设坠物为尖锐的楔体，因而计算得到的凹痕值较大，导致Monte Carlo法计算的可靠度指标偏小。绝大多数计算点落在±20%的相对误差线范围内，仅有2个点落在误差线外，但其可靠度指标的绝对误差分别为0.05和0.06。所有工况中绝对误差最大为0.500，最小为0.05，平均为0.217；相对误差最大为21.39%，最小为4.23%，平均为13.67%。

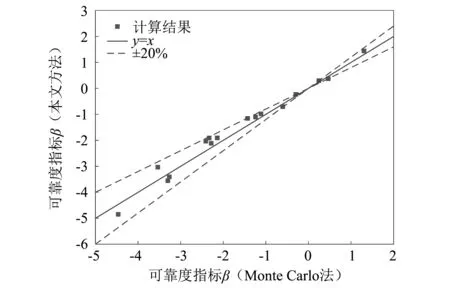
图4 可靠度指标对比Fig.4 The comparisons of reliability index

分析误差产生的原因，可归纳为两类因素：①来自于管道凹痕深度计算方法的差异。本文提出的方法中采用非线性有限元法计算管道的损伤，可考虑材料、接触条件及边界条件的非线性因素，因而可获得更为精确的结果。而Monte Carlo法采用的则是计算公式法，对实际条件进行了简化，忽略了坠物与管道间的相互作用，无法客观描述物体间的接触，尤其当需考虑坠物形状及管道-海床相互作用时会与实际情况存在较大偏差。②可靠度算法的差异对计算结果造成一些影响。响应面法主要在管道的失效域附近设置试验点，有些情况可能会影响设计验算点的收敛效果从而引起部分偏差。

从总体上看，该可靠度计算模型的结果与Monte-Carlo法的结果相差不大，平均相对误差控制在15%以内，说明该模型的计算结果是合理的，同时考虑了材料、接触等非线性因素，更为符合实际情况。

3 分析讨论

3.1 管土耦合作用对损伤的影响

海底管道通常安置在海床表面或埋置于海床土体中，现分析上述因素对管道损伤的影响。考虑海床土体为均质黏土，计算管道在柔性海床及埋深(e=0.5 m)条件下受坠物撞击时(E=28.9 kJ)的损伤情况，并与刚性海床条件下的情况进行对比。

计算结果如图5所示，从两方面进行分析。①管道损伤的分布：在刚性海床的条件下，由管道的位移云图可看出，管道损伤的凹痕深度在撞击中心处最大，并向四周扩散，近似成椭圆形分布，此时冲击能量几乎全部被管道塑性变形所吸收。而在海床柔性及埋深的条件下，位移云图的分布范围逐渐向管道撞击中心靠拢，其损伤区域的面积不断减小。②管道损伤的最大凹痕深度：管道裸落在刚性海床上变为埋置于海床内，撞击中心处横截面的凹痕深度由则0.18D逐渐减小至0.06D。这是由于在撞击过程中，一部分冲击能量被管道周围的土体变形及管道的整体位移所耗散，减缓了管道的损伤范围及深度，这与Zeinoddini等和姜逢源等得到的结论是一致的。分析可知，海床柔性及埋深对管道的损伤影响较大，不考虑该因素时得到的结果偏保守。因此，在可靠度分析中需考虑上述因素：使用Python编程建立相应条件下的有限元模型并嵌入到可靠度分析程序。

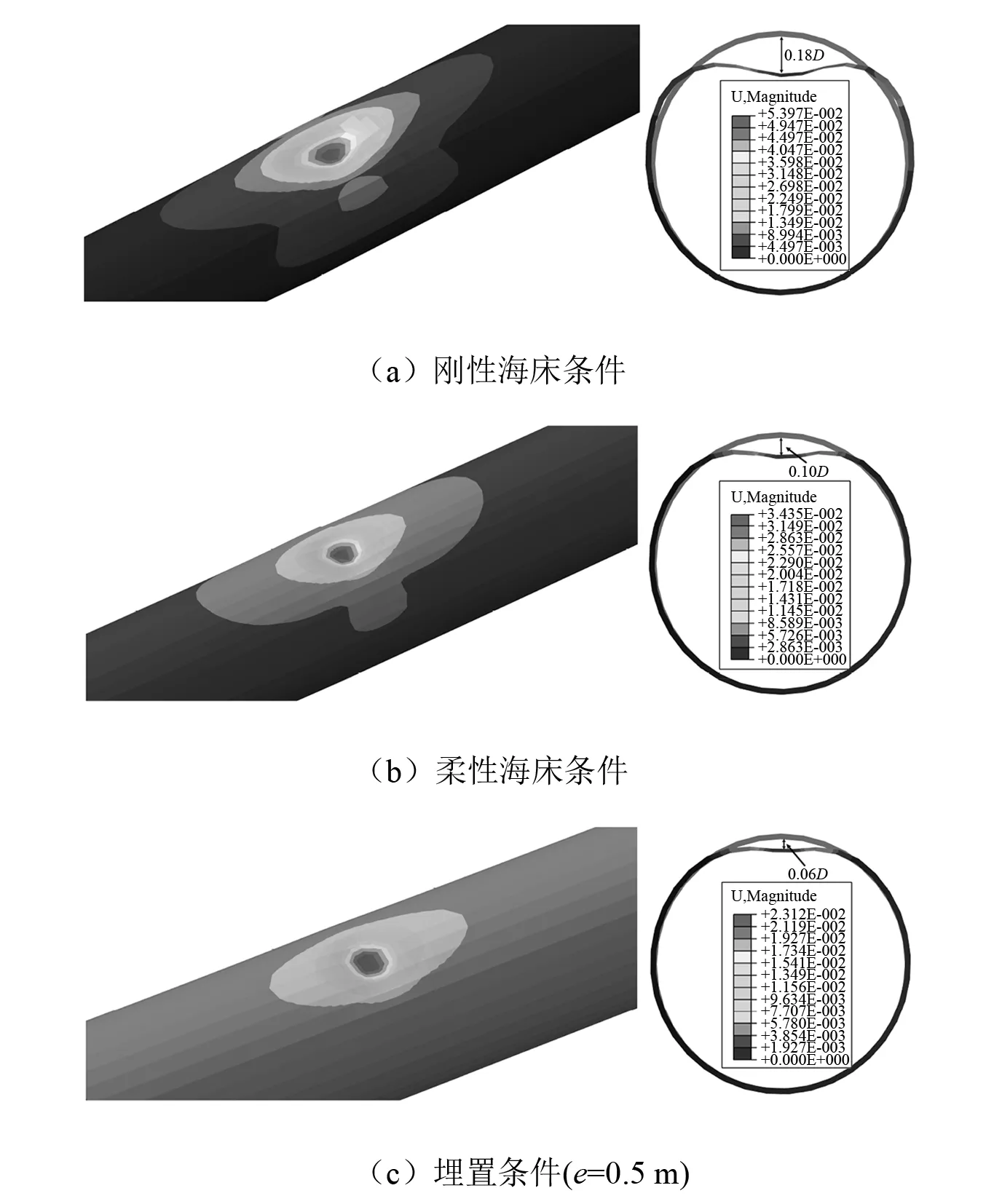
图5 不同条件下管道的位移云图及凹痕深度Fig.5 Pipeline displacement contour and dent depth in different conditions

3.2 实例分析

图6为某管道工程的平面布置图，该工程所在地水深d=100 m，所在海域坠物的平均质量为900 kg左右；海床土体为均质黏土(不排水抗剪强度Su=10 kPa)；管道西南侧距坠物点的距离为60 m，向东北方向延伸150 m，管道钢材料的屈服强度σy=360 MPa,管道外径D=324 mm，壁厚t=12 mm。

图6 海底管道布置图(m)Fig.6 Filed layout of submarine pipeline(m)

现分析管土相互作用对管道失效风险的影响，简化坠物为质量m=900 kg、速度v=10 m/s球状坠物，计算该管道在三种海床条件(①刚性海床；②柔性海床；③埋深e=0.5 m)下，受坠物撞击时的可靠度指标β及相应的失效概率Pf=1-Φ(β)。结果如图7所示。三种条件下管道的可靠度指标分别为-4.85，2.93和5.21。海床柔性及埋深会大大提高管道的可靠度指标，使其失效概率由1逐渐降低至10-7，对海底管道进行埋深处理是一种有效的保护措施。

图7 不同海床条件下管道的可靠度指标及失效概率Fig.7 Reliability index and failure probability for pipeline under different seabed conditions

根据图6中管道的铺设路径及坠物点的空间位置关系可求出坠物撞击管道的概率Ph，具体计算方法可参考DNV法，则最终管道的总失效概率为Pf,t=Ph×Pf。图8给出了三种条件下管道总失效概率沿管道长度方向的空间分布，并与DNV法的结果进行了对比。由结果可知：①刚性海床条件下管道总失效概率的计算结果与DNV法的结果十分接近，因为二者均忽略了管土相互作用的影响；②失效概率随着管道距起点距离的增加迅速减小，对于刚性海床情况，距起点的距离大于40 m后其失效概率小于10-5，满足一般工程的安全标准，故应对前40 m内的管道段进行重点保护；③柔性海床条件下最大的失效概率为10-6，为刚性海床条件下的千分之一，可见DNV法未考虑土体对冲击能量的耗散，计算结果偏于保守；④埋深条件下，管道的最大失效概率仅为10-10，这是因为管道上覆土体的剪切破坏过程需消耗大量能量，最终有效保护了管道。

3.3 埋深对失效概率的影响

由3.2节分析可知，埋深极大提高了管道可靠性。为进一步探究其影响，另选3种工况，计算不同埋深条件下(e=0.5 m，0.75 m，1.0 m)管道的可靠度指标及失效概率，计算结果如图9所示。其中，坠物为球状，相关参数为：①m=3 500 kg，v=9.06 m/s；②m=2 750 kg，v=8.71 m/s；③m=2 000 kg，v=8.07 m/s。管道参数：σy=538 MPa，D=324 mm，t=12 mm。可以看出，管道受撞击时的失效概率随着埋深的增加而呈非线性降低。对于工况2的情况，0.5 m或0.75 m的埋深时管道的失效概率均大于10-5，其不足以有效的保护管道，直至埋深增加至1 m时，其失效概率才控制在可接受的范围内。但对于工况1来说，冲击能量进一步增大，1 m的埋深也不足以保护管道，还需增加埋深或采取其他的保护措施。因此，为选择合理的管道埋深，应以该海域内典型的坠物冲击为目标进行设计。

图8 管道失效概率沿管道长度的空间分布Fig.8 Spatial distribution of failure probability along the length of pipeline

图9 不同埋深下管道的可靠度指标及失效概率Fig.9 Reliability index and failure probability for pipeline with different burial depth

此外，Zeinoddini等和姜逢源等研究中还指出海床土体的力学特性也对冲击能量的耗散有着重要的影响，故对其也应进行考虑。图10为埋深e=0.5 m时，在工况2条件下管道的可靠度指标及失效概率随土体强度的变化曲线。可以看出，随着土体强度的增加，管道的失效概率逐步下降，并且下降的趋势随着土体强度的增加而越发明显，这可从姜逢源等研究中的结果得到印证：对于埋置管道，随着土体强度的增加，管道损伤的凹痕值的减少量逐渐增大。

3.4 随机变量的灵敏度分析

进行可靠度分析时，选取了σy，D，t作为随机变量。由于设计和施工等因素，相关参数需要进行调整，为分析上述因素的变异性的影响，以3.3节中工况3为例，即以μσy=448 MPa，cvσy=0.07；μD=324 mm，cvD=0.03;μt=12 mm，cvt=0.05为基准，分别取其0.8倍、0.9倍、1.0倍、1.1倍、1.2倍，计算在质量为m=2 000 kg的球状坠物撞击(v=8.07 m/s)埋深e=0.5 m的海底管道时的可靠度及失效概率，结果如图11和图12所示。

图10 管道的可靠度指标及失效概率随土体强度的变化Fig.10 Reliability index and failure probability for pipeline with different soil strength

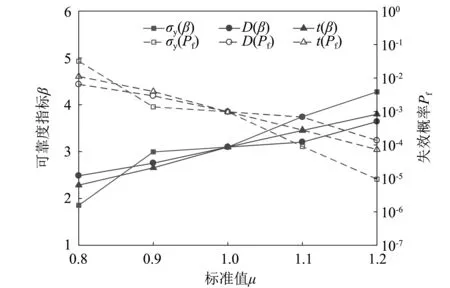
图11 可靠度指标及失效概率随均值的变化Fig.11 Reliability index and failure probability with different means

分析可得：①当均值发生变化时，屈服强度σy的影响效果最为显著，可靠度指标从1.85上升至4.28，其次为壁厚t，再次为管径D。说明管道材料的屈服强度的增加明显提高了管道抵抗冲击的承载力，而壁厚与塑性弯矩呈2次方关系，其影响效果也较为明显。②当变异系数发生变化时，可靠度指标随着cvσy的增加而下降，其失效概率发生了量级上的变化，由10-4迅速增加到10-2，因而在对钢材的力学强度进行检测时要严格把控其质量。而对于cvD及cvt的变化，可靠度指标仅发生微小的波动，受管径D及壁厚t变异性的影响较小。

图12 可靠度指标及失效概率随均值的变化Fig. 12 Reliability index and failure probability with different variable coefficients

4 结 论

本文将非线性及管土耦合作用引入风险分析中，利用非线性有限元分析法与响应面法耦合，构建了海底管道受坠物撞击的可靠度分析方法，并与Monte Carlo法对比，验证了其合理性，同时分析了管土耦合作用对管道失效概率的影响，得到以下结论：

(1)基于Python二次开发技术，将非线性有限元分析模块嵌入响应面法中构建了可靠度分析模型，实现了求解算法与有限元分析之间的信息传递、迭代等工作，该技术可拓展到其他相关领域，如结构的参数优化等。

(2) 由实例分析可知，管道的失效概率沿管道起点距离逐渐减小，前40 m范围内的失效概率较大，应重点进行保护；与刚性海床条件相比，柔性海床条件下管道的失效概率为前者的10-3；埋深条件下，管道的最大失效概率仅为刚性海床条件下的10-7，极大提高管道的安全性；综上，不考虑管土相互作用时结果偏保守；

(3) 增加埋深能明显降低管道的失效风险，但冲击能量较大时(约145 kJ)，1 m埋深时管道的失效概率仍大于10-5，不足以提供安全保障。故在选择合理的埋深时，应针对该海域内坠物的典型坠物附带的冲击能量作为设计埋深，同时也要考虑到海床土体的力学特性。

(4) 随机变量敏感性分析，当各变量的均值以0.8～1.2倍变化时，σy对可靠度及失效概率的影响最大，其次为t及D；当变异系数以0.8～1.2倍变化时，可靠度指标随cvσy增大而减小，失效概率发生量级上的增加；其余两变量的变异系数对结果的影响不大，工程建设中，检测时应严格把控钢材的材质。

本文提出的有限元-响应面耦合可靠度模型首次应用于管道的风险分析中，建立了管道风险与埋深间的关系，该模型及研究结果可为工程设计提供有效指导。未来，将在模型中考虑更多因素的作用，如坠物种类、尺寸，土体材料等影响。