海底光电复合缆受坠物撞击损伤分析

李 英， 王 坤

(天津大学 建筑工程学院 水利工程仿真与安全国家重点实验室， 天津 300350)

0 引 言

随着风电逐渐向远海发展，海底电缆在海上风力发电及输电上的应用将拥有广阔的市场前景。海底电缆发生故障会影响当地正常的生产和生活，且其维修费用昂贵，因此海底电缆的安全应引起足够的重视。影响海底电缆安全的其中一个关键问题是坠物撞击海底电缆，因此开展坠物撞击海底电缆的研究对保障海底电缆安全稳定运行具有十分重要的意义。目前，国内外对坠物撞击管道研究较多，海底电缆受坠物撞击的文献相对较少，可参考管道受坠物撞击影响的文献研究海底电缆受坠物撞击的影响[1-5]。光电复合缆受坠物撞击损伤的分析方法主要为数值模拟法和试验研究法[6-9]。为深入理解坠物撞击对海底光电复合缆造成的损伤，并进一步为海底光电复合缆的防护措施设计提供依据，本文基于耦合欧拉-拉格朗日(Coupled Eulerian-Lagrangian，CEL) 方法对坠物撞击海底光电复合缆进行数值模拟，对刚性底质和非刚性底质两种工况进行损伤对比分析，并研究坠物大小、最终撞击速度、坠物质量和撞击角度对海底光电复合缆损伤的影响。

1 坠物撞击海底光电复合缆有限元模型

1.1 模型简化

所研究的电缆是型号为AXBTV 170 kV的单层铠装光复合型电缆，其横截面如图1所示。由于主要研究内容是海底电缆受坠物撞击后的力学性能,因此建模时结构强度低、厚度小的垫层、绝缘层和阻水层等可以作简化处理，简化后的横截面如图2所示。该光电复合缆的主要参数如表1所示，材料基本参数如表2所示。

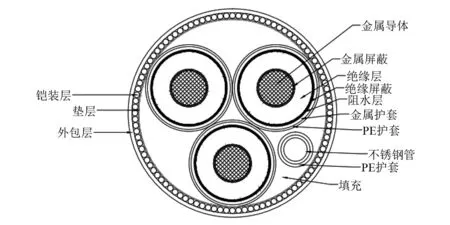
图1 海底光电复合缆横截面

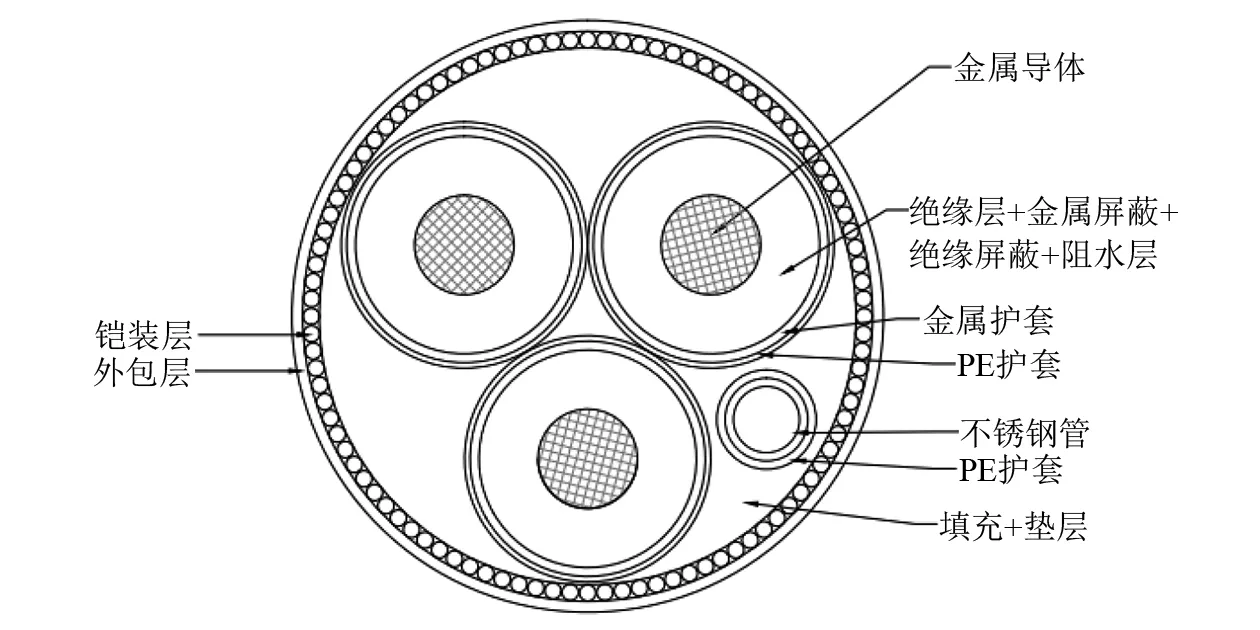
图2 简化后海底光电复合缆横截面

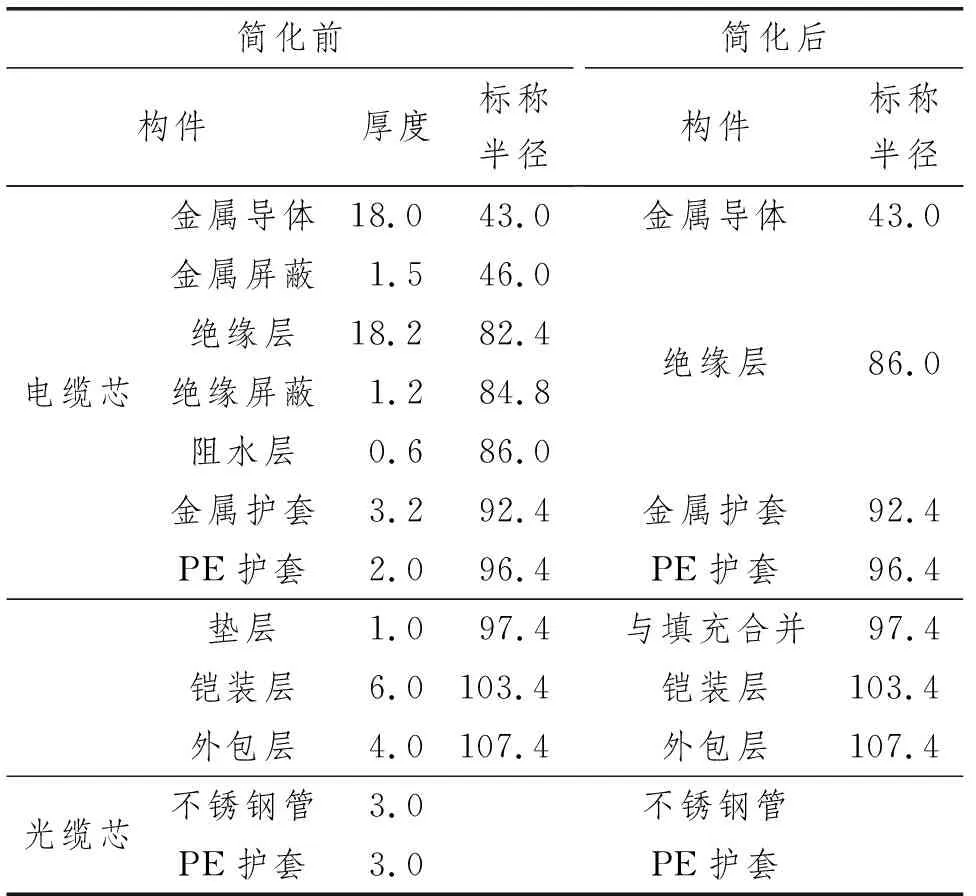
表1 海底光电复合缆模型主要参数

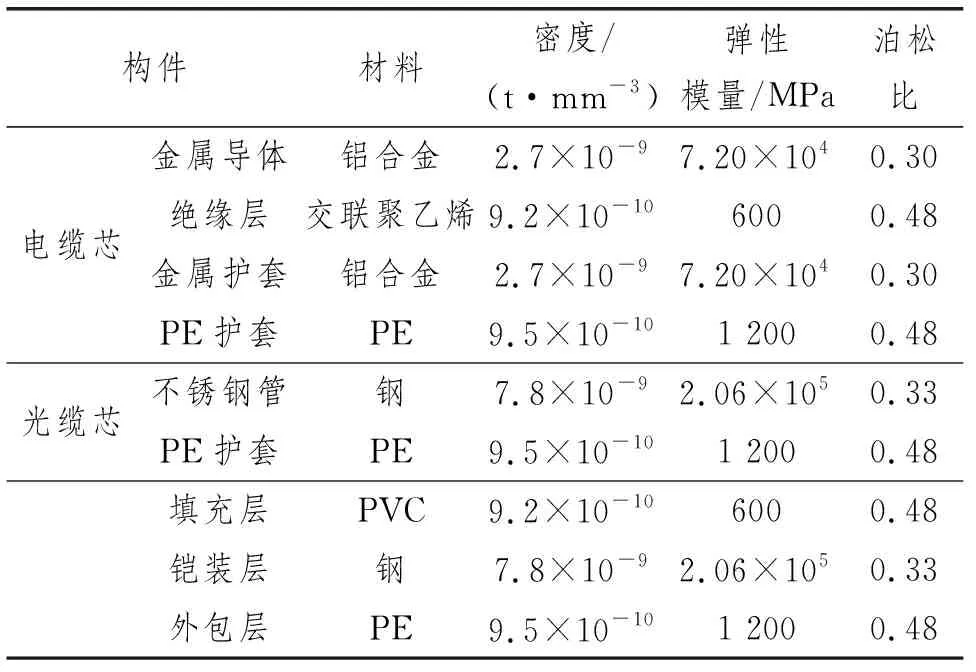
表2 海底光电复合缆材料基本参数

1.2 坠物撞击海底光电复合缆有限元模型

建立坠物、海底光电复合缆和海床的有限元模型，对坠物撞击海底光电复合缆的动态冲击过程进行仿真。海底光电复合缆铠装层螺距为3.6 m，电缆芯螺距为2.3 m，电缆的模型长度为2个铠装层螺距7.2 m。不考虑坠物的损伤，将质量为312 kg 的正方体坠物约束为刚体。对于刚性底质，不考虑撞击过程中土体的变形，将海床模拟为刚体,其有限元模型如图3所示；对于非刚性底质，考虑撞击过程中土体发生的非线性大变形，将海床模拟为欧拉体，其本构模型选择Mohr-Coulomb模型，有限元模型如图4所示，材料参数如表3所示。由于海底光电复合缆各层之间的接触非常复杂，因此设置为通用接触。

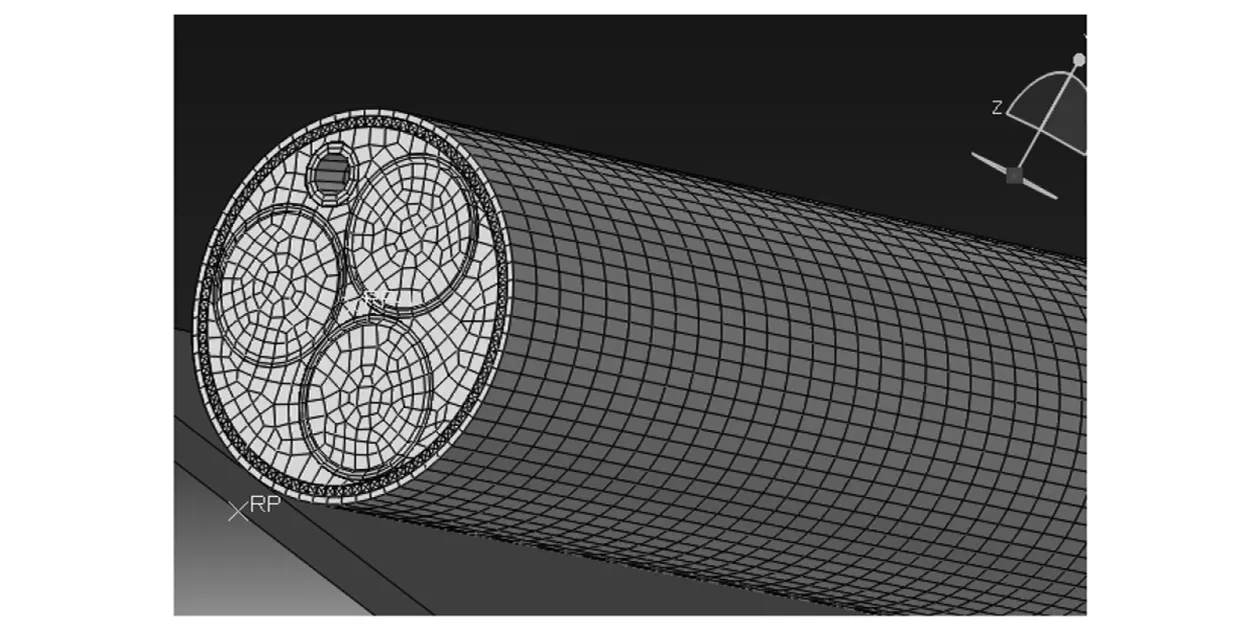
图3 刚性底质海底光电复合缆有限元模型

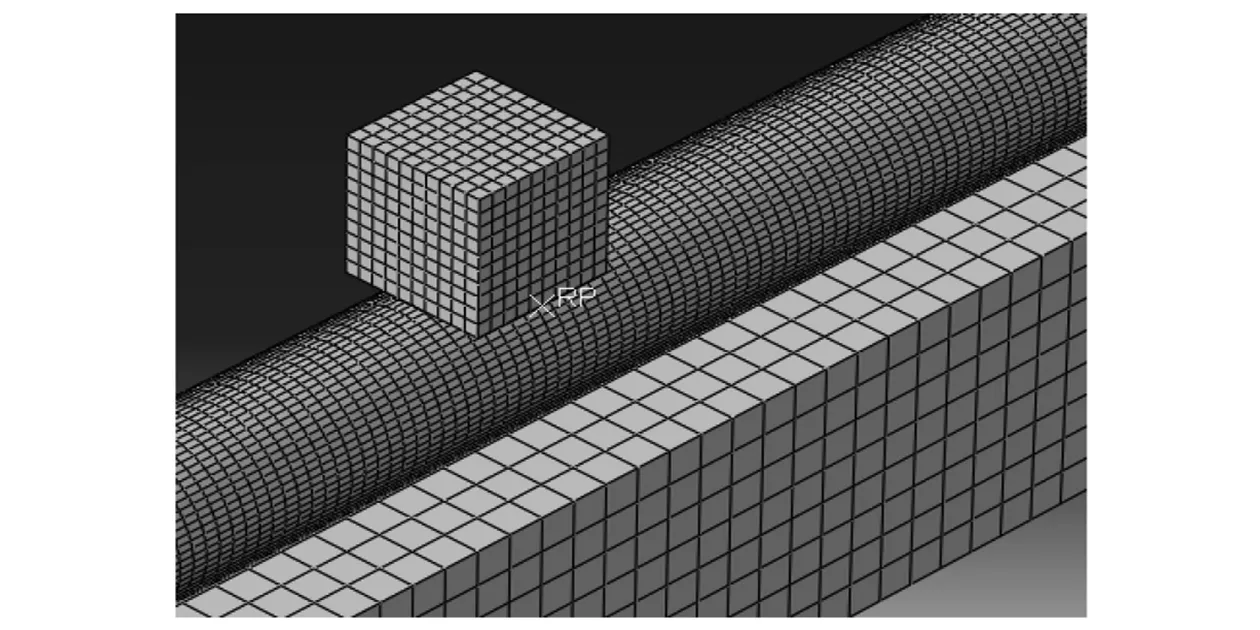
图4 非刚性底质海底光电复合缆有限元模型

表3 非刚性底质土体材料参数

2 海底光电复合缆受撞击时损伤分析

2.1 坠物撞击海底光电复合缆过程中的能量变化

与坠物撞击管道过程类似，坠物撞击海底光电复合缆的过程本质也是非线性接触、能量转换过程。刚性底质上海底光电复合缆总动能和总内能变化如图5所示，非刚性底质上海底光电复合缆总动能和总内能变化如图6所示。由于刚性底质上海床不发生变形，对能量没有吸收作用，因此在1个撞击周期(坠物撞击至被弹开)内能量变化与非刚性底质相比相对简单且撞击周期短，但能量变化趋势与非刚性底质保持一致。

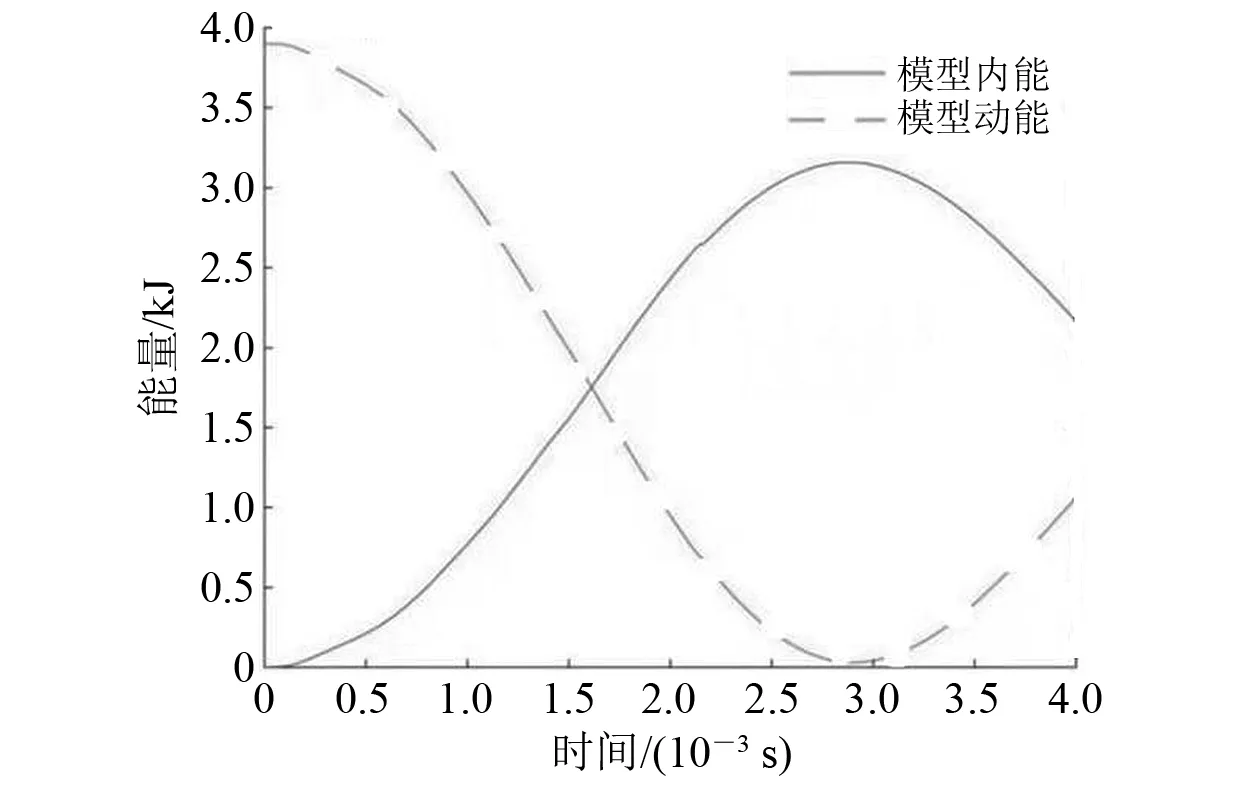
图5 刚性底质撞击过程中总动能和总内能随时间变化曲线

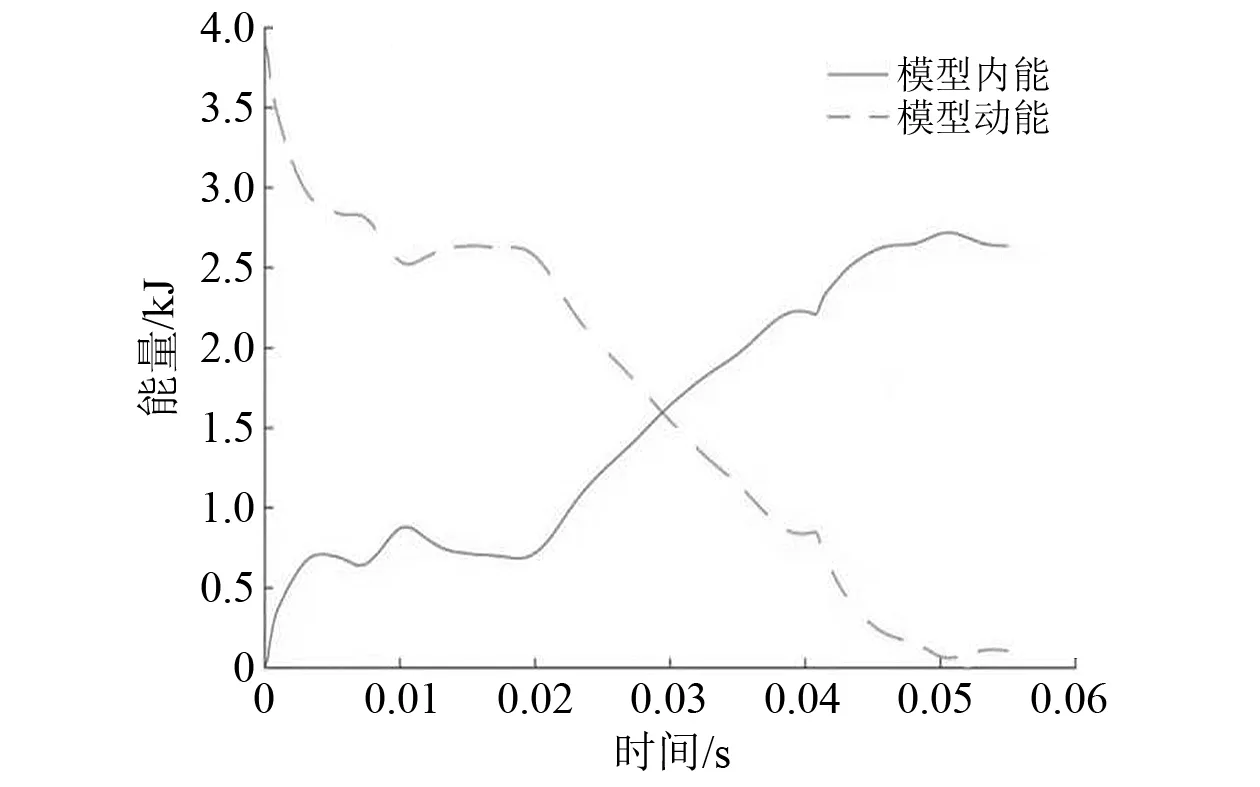
图6 非刚性底质撞击过程中总动能和总内能随时间变化曲线

2.2 坠物撞击海底光电复合缆过程中的应力和应变

图7为非刚性底质上1个撞击周期内铠装层最大von Mises 应力时程曲线。图8为刚性底质上1个撞击周期内铠装层最大von Mises应力时程曲线。由图7和图8可知：在非刚性底质上，由于海床对能量的吸收作用，铠装层上的最大应力有一个随作用时间延长而下降的过程，且作用在铠装层上的最大应力明显小于刚性底质上作用在铠装层的最大应力。

图9为非刚性底质上铠装层发生的最大等效塑性应变。图10为刚性底质上铠装层发生的最大等效塑性应变。对比图9与图10可知，刚性底质上发生的最大等效塑性应变明显大于非刚性底质。由此可推断，在实际工程中在较硬的海床上铺设海底光电复合缆需要施加更多的保护措施。为更直观地获得坠物撞击海底光电复合缆对海底光电复合缆造

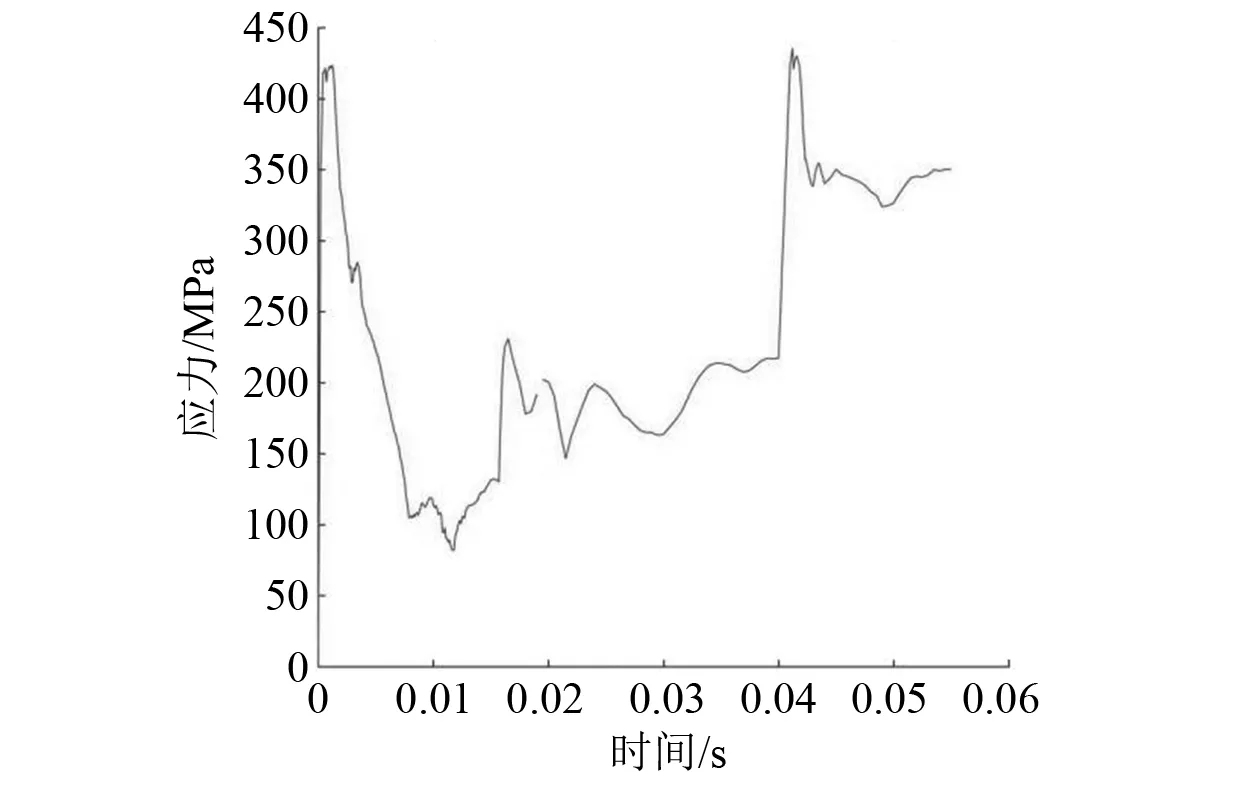
图7 非刚性底质铠装层不同时间最大应力时程

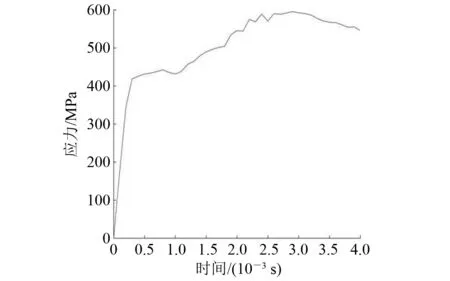
图8 刚性底质铠装层不同时间最大应力时程

成的损伤，进一步分析海底光电复合缆损伤因素的敏感性，第3节的分析均采用刚性底质。

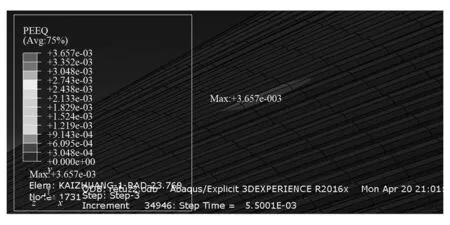
图9 非刚性底质铠装层等效塑性应变云图

图10 刚性底质铠装层等效塑性应变云图

2.3 铠装层和电缆芯的等效塑性应变

图11和图12分别为坠物撞击海底光电复合缆过程中铠装层和电缆芯等效塑性应变最大点的等效塑性应变时程曲线。由图11和图12可知：在坠物撞击海底光电复合缆的过程中，铠装层和电缆芯的等效塑性应变变化趋势一致。因此，可通过外部铠装层的损伤变形推断电缆芯的损伤变形，这对在实际工程中判断海底光电复合缆的损伤变形具有十分重要的意义。

图11 铠装层等效塑性应变

图12 电缆芯等效塑性应变

3 海底光电复合缆损伤因素分析

3.1 坠物大小对海底光电复合缆的影响

坠物大小与海底光电复合缆受力面积直接相关，因此坠物大小是影响海底光电复合缆受坠物撞击损伤的关键因素之一。以质量为312.0 kg的正方体坠物为例，建立坠物边长以50 mm为间隔、由100 mm增长至300 mm的计算模型。根据数值模拟计算结果，得到不同坠物大小海底光电复合缆铠装层发生的等效塑性应变，其变化趋势如图13所示。

由图13可知：海底光电复合缆铠装层的等效塑性应变随坠物边长的缩短而增大，即在同等质量下，坠物越小，海底光电复合缆受到的损伤越大。但边长为150 mm和200 m的坠物产生的铠装层等效塑性应变几乎相同，这可能与海底光电复合缆直径有关。

3.2 撞击速度对海底光电复合缆的影响

海底光电复合缆所受撞击能量与坠物的撞击速度直接相关，因此坠物撞击速度是影响海底光电复合缆受坠物撞击损伤的关键因素之一。以质量为62.0 kg的正方体坠物为例，分别建立撞击速度为3.50 m/s、3.70 m/s、3.85 m/s、4.00 m/s、4.20 m/s、4.35 m/s、4.50 m/s、4.70 m/s、4.85 m/s、5.00 m/s、5.20 m/s、5.35 m/s、5.50 m/s、5.70 m/s、5.85 m/s、6.00 m/s的计算模型。根据数值模拟计算结果，得到不同撞击速度下海底光电复合缆铠装层发生的等效塑性应变，其变化趋势如图14所示。

图14 不同撞击速度下铠装层等效塑性应变

图14表明海底光电复合缆铠装层的等效塑性应变随撞击速度的增高而增大，即撞击海底光电复合缆的速度越高，海底光电复合缆受到的损伤越大。

3.3 坠物质量对海底光电复合缆的影响

海底光电复合缆所受撞击能量还与坠物的质量直接相关，因此坠物质量也是影响海底光电复合缆受坠物撞击损伤的关键因素之一。以撞击速度为5.00 m/s的正方体坠物为例，建立坠物质量以31.2 kg 为间隔、由62.4 kg增大至374.4 kg的计算模型。根据数值模拟计算结果，得到不同质量坠物的撞击下海底光电复合缆铠装层发生的等效塑性应变，其变化趋势如图15所示。

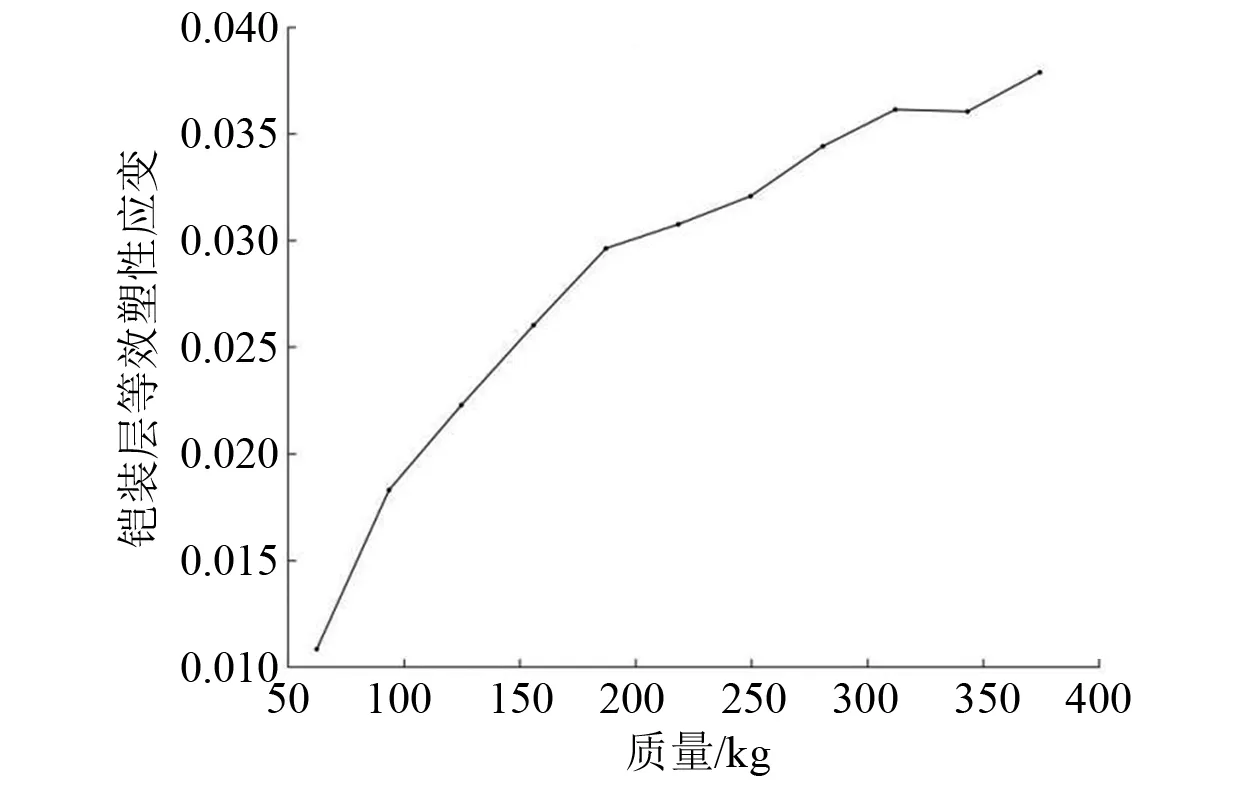
图15 不同撞击质量下铠装层等效塑性应变

由图15可知：海底光电复合缆铠装层的等效塑性应变随坠物质量的增大而增大，即撞击海底光电复合缆的坠物质量越大，海底光电复合缆受到的损伤越大。

3.4 撞击角度对海底光电复合缆的影响

坠物在海水中运动时可能受到波浪等因素的影响发生旋转，导致最终撞击海底光电复合缆的角度(坠物与海床的夹角)不同。为研究坠物撞击海底光电复合缆的角度对海底光电复合缆损伤的影响，以撞击速度为5.00 m/s、质量为62.0 kg的正方体坠物为例，建立以5°为间隔、撞击角度由15°变化至85°的数值模型，模拟结果如图16所示。与第3.1～第3.3节的工况相比，此时正方体的棱接触海底光电复合缆，发生的塑性应变相对较大。

由图16可知：当撞击角度小于60°时，海底光电复合缆铠装层发生的等效塑性应变随撞击角度的增大而增大；当撞击角度为60°时，海底光电复合缆铠装层发生的等效塑性应变最大，海底光电复合缆的损伤最严重；当撞击角度大于70°时，海底光电复合缆铠装层发生的等效塑性应变快速下降，这是由于随撞击角度变化，正方体坠物的重心位置发生改变。

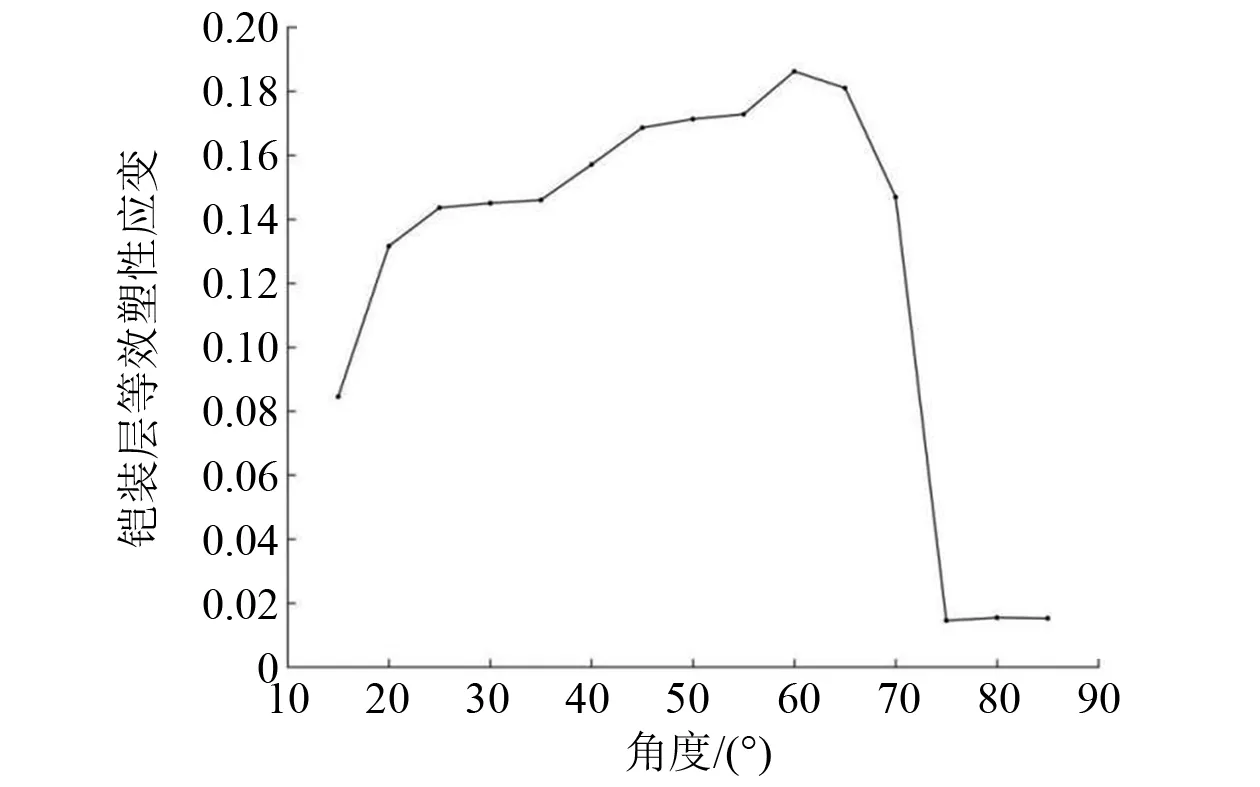
图16 不同撞击角度下铠装层等效塑性应变

4 结 论

由铠装层的能量变化曲线可知坠物撞击海底光电复合缆的过程是一个能量转换的过程。研究坠物大小、坠物质量、撞击速度和撞击角度对海底光电复合缆铠装层和电缆芯的应力应变得出如下结论：

(1) 刚性底质上发生的最大等效塑性应变明显大于非刚性底质。由此可推断，在实际工程中在较硬的海床上铺设海底光电复合缆需要施加更多的保护措施。

(2) 铠装层是海底光电复合缆的主要承力构件，在工程实际中可通过监测铠装钢丝的损伤变形推断电缆芯的损伤变形。

(3) 海底光电复合缆受坠物撞击后的损伤结果与坠物大小有关，对于同等质量的坠物，坠物越小越容易对海底光电复合缆造成较大的损伤。

(4) 海底光电复合缆受坠物撞击后的损伤结果与坠物的质量和最终撞击速度有关，坠物的质量和最终撞击速度越大，越容易对海底光电复合缆造成较大的损伤。因此，铺设在较大船只频繁通行海域内的海底光电复合缆需要施加更多的保护措施。

(5) 海底光电复合缆受坠物撞击后的损伤结果与坠物的撞击角度有关，对于正方体坠物，当撞击角度为60°时，海底光电复合缆受到的损伤最大，表明撞击最大的角度并不是垂直方向，这与坠物的形状和重心分布有关。