FPSO一体化变形简化计算方法

韦 琪， 谷家扬,1b， 渠基顺,1b， 李 荣， 万家平

(1. 江苏科技大学 a. 船舶与海洋工程学院； b. 海洋装备研究院， 江苏 镇江 212003；2. 南通中远海运船务工程有限公司， 江苏 南通 226001)

0 引 言

传统浮式生产储卸油装置(Floating Production Storage and Offloading，FPSO)结构设计将上部模块与主船体按界面切割分开考虑，先计算得到船体梁的变形作为上部模块桁架结构的边界约束，而忽略上部模块桁架刚度对船体变形的影响，也忽略船体梁局部结构变形；另一方面支墩设计时也忽略了整个桁架与船体之间的耦合作用，往往会导致设计方案过于保守或存在安全隐患。本文主要研究上部模块与主船体一体化时，即考虑上部模块与主船体两者耦合情况下，主甲板垂向变形的简化计算方法，并将简化计算结果与整船有限元分析结果进行对比，验证简化计算方法的准确性与适用性。

针对上部模块变形问题，徐田甜[1]在FPSO的船体刚度分析中指出，上部模块受船体总纵弯曲影响，模块基座在甲板支墩处主要考虑船体垂向与纵向变形，通常每座支墩纵向跨距控制在0.1倍船长以内。MESPAQUE等[2]以巴西石油公司P-53平台为例，进行FPSO船体与上部模块互相作用的试验分析，分析整个过程中船体与上部模块的相互作用，为该模块及其甲板上支撑物的结构设计提供参考。HENRIKSEN等[3]研究上部模块所受载荷主要包括：船体梁变形引起的载荷；FPSO储罐的压力载荷及船舶运动引起的惯性载荷。TERPSTRA等[4]指出，在考虑上部模块对船舶整体结构的影响时，不仅需要考虑上部模块的自重，而且当上部模块支撑的管路开始工作后，管路内液体重量可能占模块重量的20%。MACHADO等[5]研究FPSO上部模块与主船体连接形式的屈曲与疲劳问题，针对该问题提出3种支撑方案：第1种采用横向舱壁支撑每个上部模块；第2种采用底凳形式支撑每个上部模块；第3种采用桁架形式支撑每个上部模块。KREKEL等[6]也研究桁架支撑的形式，指出桁架支撑的重量适用于重量达500 t的上部模块，缺陷是桁架结构是静不定结构，在设计阶段需要考虑足够的安全裕量以应对反作用力的不确定性。廖红琴[7]和张明等[8]针对FPSO上部模块结构规划需要考虑的主要问题，参照美国石油协会(API)和美国钢结构协会(AISC)的规范指出，在强度校核中应考虑风、浪、流等环境载荷对船体运动和甲板变形的影响。

1 有限元变形计算

本船一体化结构模型的建立基于有限元建模MSC.Patran软件，船体结构大多为板梁结构，在有限元中使用二维板单元(Shell)和一维杆梁单元(Beam)进行模拟[9-13]。模型相关材料属性如下：弹性模量E=2.01×1011Pa；泊松比ν=0.3；密度ρ=7 850 kg/m3。全船模型共计902 017个单元、361 272个节点。详细整船与上部模块有限元模型如图1所示。

图1 整船与上部模块有限元模型

垂向变形分析均基于变形最大的满载工况进行研究，有限元变形计算采用设计波法计算波浪载荷，将波浪载荷映射至结构模型上，再将货物压力、加速度等载荷施加到模型上，计算得出各模块支腿变形如表1所示。

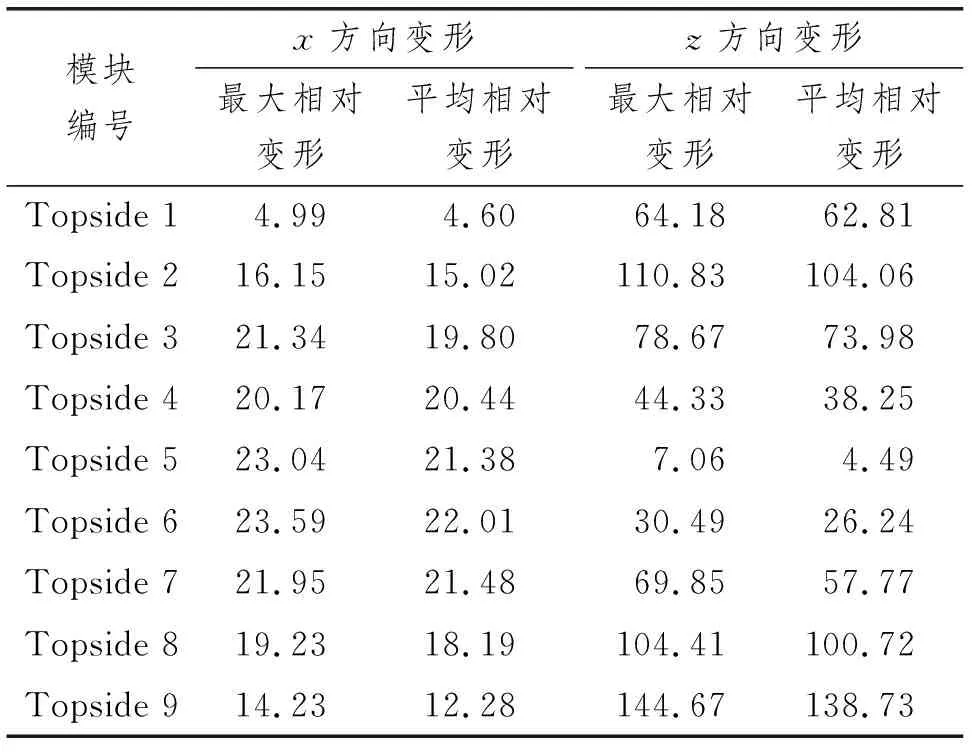
表1 各模块支腿相对变形 mm

2 DNV经验公式计算

文献[14]指出甲板变形对上部模块设计的影响一般不可忽略，变形量由总体结构分析得到。对船体变形(见图2)，挪威船级社(DNV)规范有如下经验公式进行估算：

(1)

式中：δ为横剖面①和②处的变形；M1为1号端面垂向弯矩；M2为2号端面垂向弯矩；Z为剖面模数；l为模块支腿①与②之间的距离。

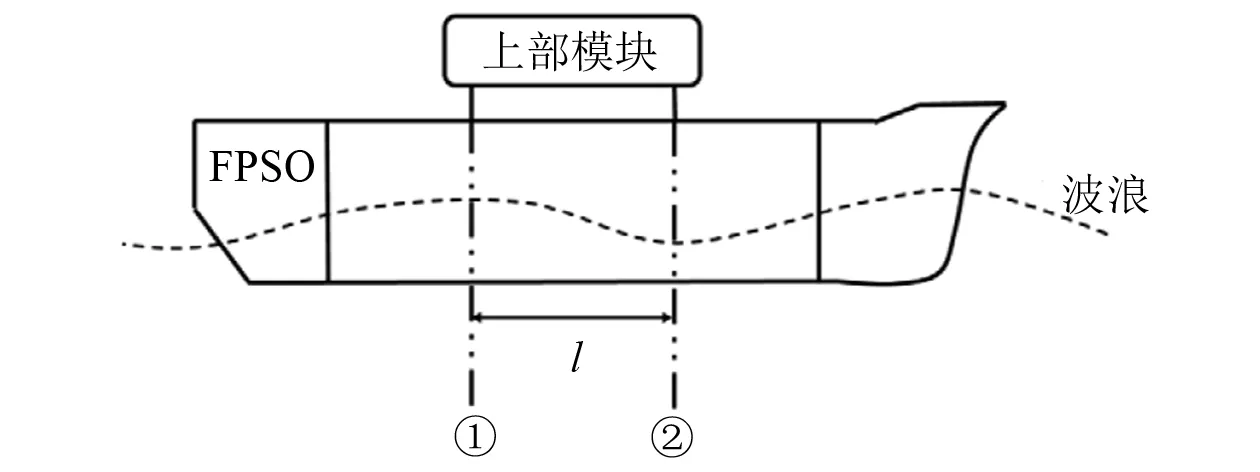
图2 上部模块变形示例

采用式(1)对各模块支腿垂向相对变形进行计算，所得数值与有限元计算值差距较大，式(1)无法作为该船舶甲板变形的经验估算方法。对式(1)进行研究，发现主导变形的主要自变量为M1与M2两个垂向弯矩之和，在计算时垂向弯矩取静水与波浪弯矩之和。本船静水弯矩与一般船舶相比存在一定差距，导致静水与波浪弯矩之和与普通船舶静水与波浪弯矩之和的变化趋势差距较大。本船静水与波浪弯矩如图3所示。

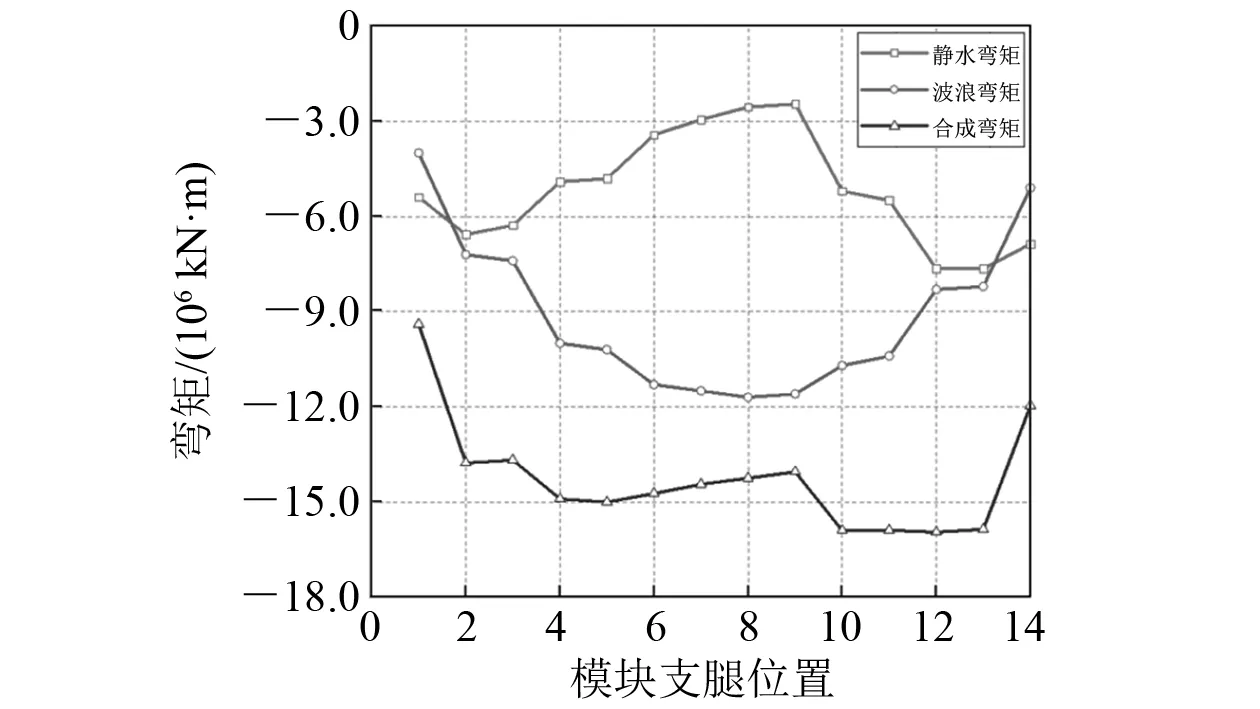
图3 FPSO静水与波浪弯矩

由图3可知：在满载状态下，船中部中垂明显小于艏艉处，导致静水与波浪弯矩叠加时船体中部的合成弯矩并没有像波浪弯矩曲线有明显的中垂趋势；接近艏部支腿时，合成弯矩几乎为水平直线，导致由式(1)计算出的2个支腿的相对变形几乎为零，与实际情况艏艉部变形较大不相符。因此，采用式(1)无法准确预报本船的相对变形值。研究发现，船体变形趋势与波浪弯矩曲线的趋势相近。因此，将波浪弯矩作为控制变形的主要输入值，为体现重量分布对船体变形的影响，将静水弯矩作为变形的修正值添加至式(1)中，修正后的公式为

(2)

式中：MS和MW分别为端面静水和波浪弯矩；E为弹性模量，取2.06×105N/mm2。

在研究过程中缺少上部模块相关的布置图纸，只有典型上部模块结构图，因此将船体上部模块均用典型上部模块代替，按总布置图建立到船体中部货舱范围内，以达到上部模块总重量的要求。在实际情况中为避免艏艉上部模块变形过大的情况，不会出现这种大跨距的上部模块。在接下来的章节里为避免无意义的工作，对艏艉上部模块不予研究，仅对Topside 2～Topside 8等7个模块变形进行研究分析。经过修正后公式计算结果如表2所示。

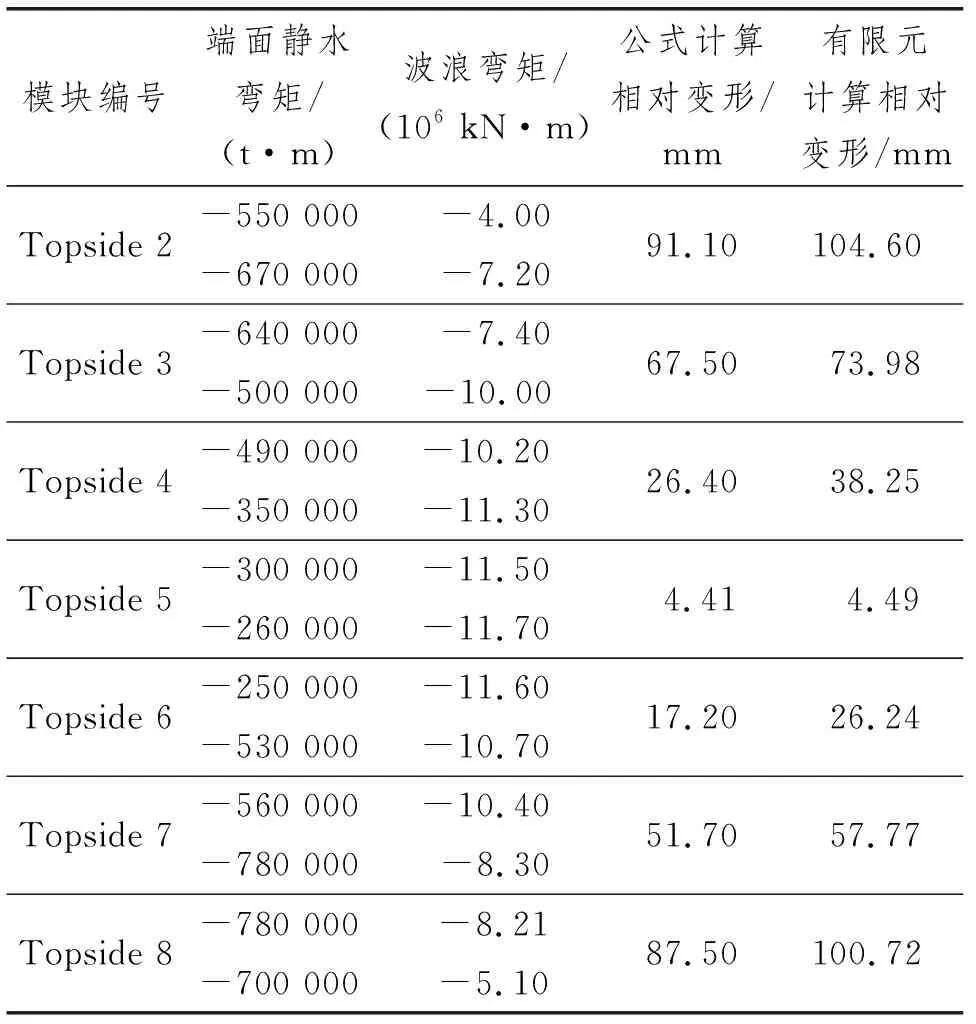
表2 修正后式(2)垂向变形估算结果

所研究模块相对变形为同一个模块相距最远的2个支腿之间的变形，因此同一模块会有2个不同对应端面数据。由表2可知：修正后垂向变形的估算公式与有限元计算的结果差距最大值为13.5 mm，最小值为0.08 mm，2种计算结果吻合度较高。由整个计算结果对比可知，经验公式的计算结果均小于有限元计算的变形结果，这是由于在采用经验公式进行计算时，将船体梁理想成1根细长的梁，计算这根梁上各个位置的垂向相对变形。在实际工程中，FPSO的船体梁还需要承受上部模块的重量，在不考虑环境载荷的影响下，本身上部模块加载在主船体上就已经造成船体的垂向变形，变形后同一模块2个支腿的相对变形几乎为零。当船体梁受到静水与波浪弯矩发生弯曲时，上部模块重心位置也随之发生改变，这种变形使上部模块2个支腿受力不均衡从而导致一边受力增大、一边受力减小的情况，从而导致由自身的重力产生的一部分垂向变形。详细受力变化如图4和图5所示。

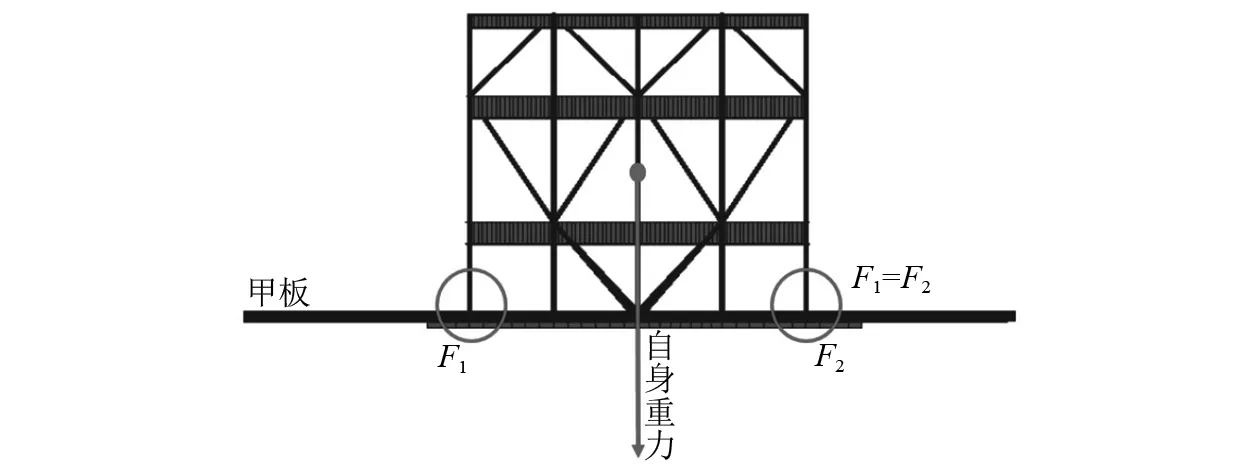
注：F1和F2为受重力作用下模块支腿所受压力图4 甲板变形前模块2个支腿受力

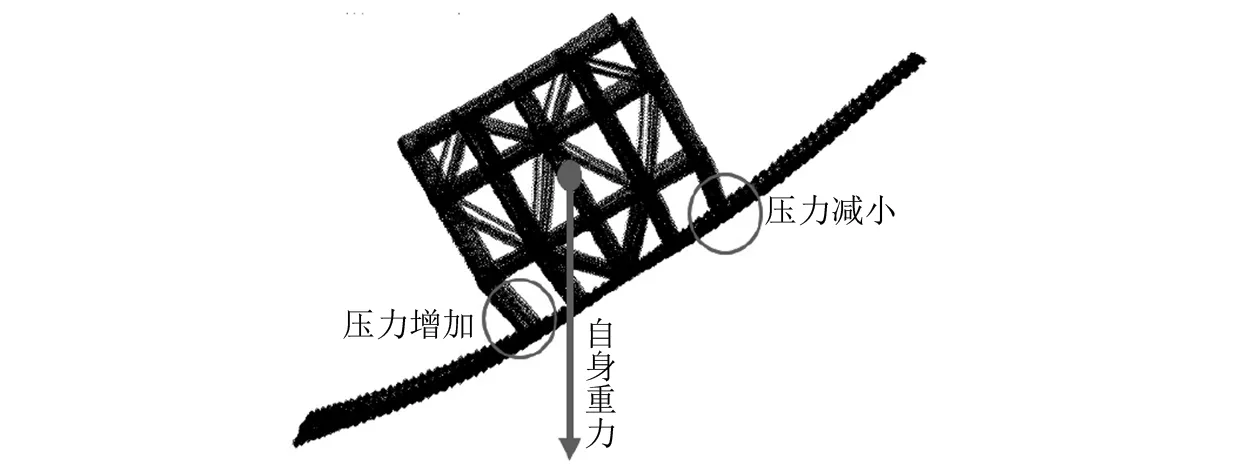
图5 甲板变形后模块2个支腿受力变化

3 国外工程方法估算

TERPSTRA等[4]提出一种工程估算方法，即将纵向船体结构理想化为一根梁，应用经典的梁挠度理论，得到相关位移估算公式。

垂向位移δZ估算公式为

(3)

式中：σ为主甲板所受弯曲应力；l1为模块长度；c为主甲板与中和轴的距离。

将计算结果与有限元分析结果进行对比，各剖面垂向相对位移均与有限元计算值有较大差距，式(3)并不适用于上部模块支腿变形分析。对式(3)计算数值与有限元数值进行详细对比，对式(3)进行修正，使计算的相对变形结果更符合有限元计算结果，修正后公式为

(4)

研究发现，经过修正后式(4)的计算结果与有限元分析的变形结果均吻合较理想，详细的计算结果与对比结果如表3所示。

除上述垂向变形估算外，国外工程中运用到的还有纵向甲板伸长率估算公式，相关估算公式为

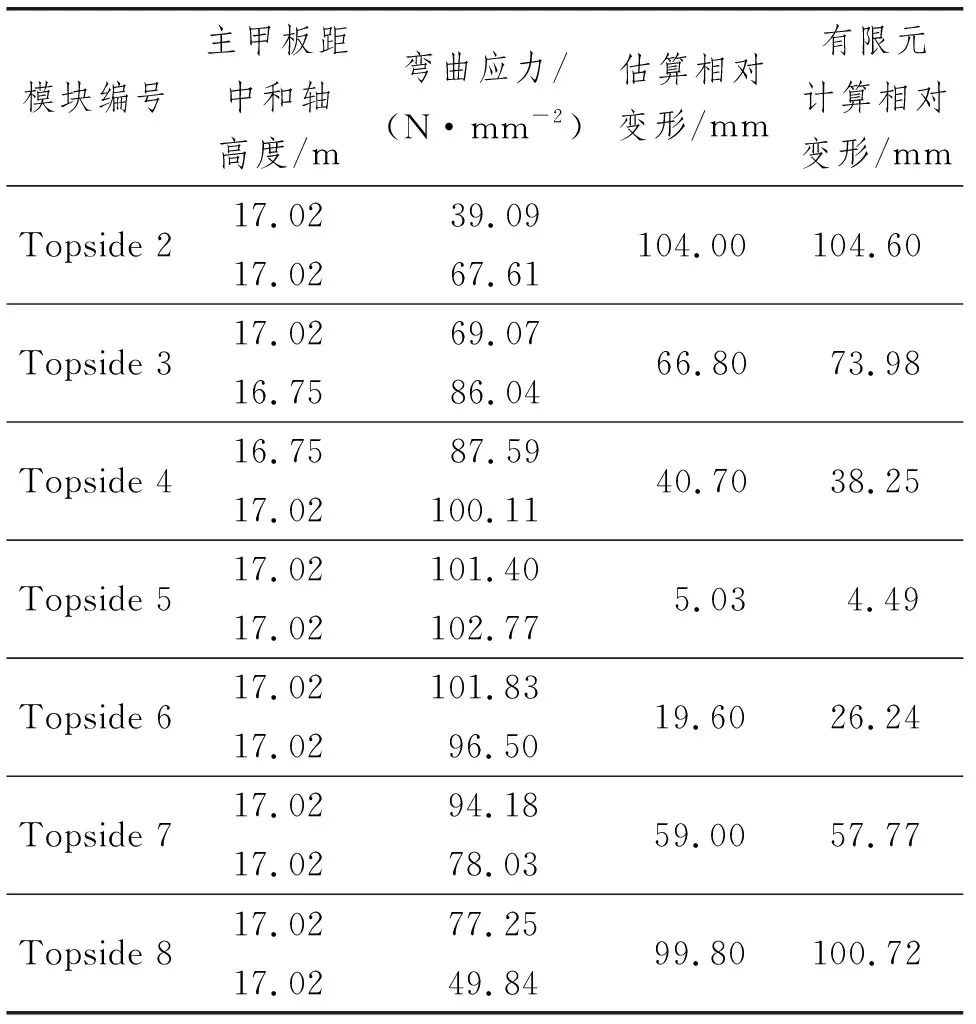
表3 修正后式(4)垂向变形估算结果

(5)

式中：δx为纵向相对变形。

采用COMPASS计算的甲板剖面模数计算出甲板的弯曲应力，利用式(5)计算纵向甲板伸长值，并与有限元变形值进行比较。详细的计算结果与比较结果如表4所示。

表4 式(5)计算结果汇总

由表3和表4可知，经过修正后的垂向变形经验公式与纵向变形经验公式计算值与有限元变形计算结果的差值均在10 mm以内，与DNV经验估算公式相比，国外工程中运用的经验公式计算值与有限元计算结果吻合度较高，其中，垂向变形最大差值为7.18 mm，纵向变形最大差值为4.29 mm。研究表明，国外工程中纵向甲板变形估算公式与经过修正后的垂向变形估算公式较适合运用到FPSO变形的估算中。

4 国内工程方法估算

在国内工程建造方面，中国船舶集团有限公司第七〇八研究所采用的简化算法在计算FPSO甲板变形时均基于船体梁的剖面模数和惯性矩沿船长不变、船体梁在垂向弯矩作用下发生的变形为等半径圆弧等假定开展的，估算模块之间垂向相对变形的详细步骤如下：

(1) 计算变形曲线半径r

(6)

式中：I为剖面惯性矩；M为各工况下的最大弯矩。

由COMPASS计算结果得出I=1 980.42 m4、E=2.06×1011Pa、静水状态下中拱与中垂弯矩许用值为1.17×1010N·m、计算波浪载荷为1.17×1010N·m、中垂工况下最大合成弯矩为2.34×1010N·m。计算得变形曲线半径r=17 400 m。

(2) 计算船中处最大变形x

(7)

式中：Lpp为垂线间长，取328.2 m。

计算得x=0.774 m。

根据有限元计算分析得出的垂向变形如图6所示。

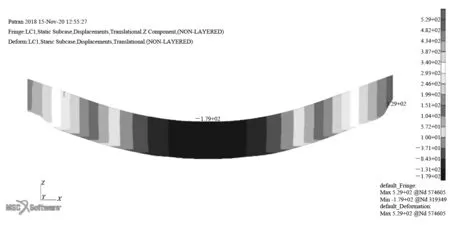
图6 有限元计算整船变形

由图6可知：船体梁首部最大形变为529 mm，中部最大变形为179 mm；整船形变为708 mm，比经验公式计算得到的774 mm减少66 mm。采用该方式估算船中最大变形偏保守。

(3) 计算船长方向变形dy

dy=rcosα-(r-x)

(8)

式中：α为各支腿肋位所在直线与圆心垂线的夹角。

dy与x关系如图7所示。

图7 公式估算整船变形示例

根据式(8)，先求出α，计算公式为

(9)

式中：l2为计算肋位与船中的距离。

在计算得出α后，根据经验公式可计算得出各模块处变形值，从而求出模块间相对变形，详细计算结果如表5所示。

表5 国内变形公式估算结果 mm

由表5可知：经验公式估算的相对变形与有限元计算的相对变形相比整体偏大，该误差可能是由船体梁局部变形产生的；除Topside 2变形差值为15.61 mm外，其余差值均控制在10 mm以内，两者差距较小。相较于DNV经验公式和国外的工程估算方法每个模块都需要根据对应剖面的静水弯矩、波浪弯矩等载荷来计算模块的相对变形，国内工程估算方法需要的自变量较少，更加能保证计算结果的精确性。

5 结 论

FPSO上部模块与主船体结构形成了整体结构，两者之间互相作用相互影响。在FPSO前期设计阶段，掌握能够考虑上部模块与主船体结构相互影响的快速评估技术对上部模块设计的安全性有至关重要的意义。

主要研究FPSO船体梁甲板变形的简化算法，即甲板变形的快速评估方法，主要研究结论如下：

(1) DNV估算公式在修正后垂向变形计算结果与有限元计算的结果最大差值为13.3 mm、最小差值为0.08 mm，2种计算结果吻合度稍微存在差距。经验公式估算法与有限元计算法的误差主要来自有限元计算方法可以得出上部模块对结构产生的局部变形，而经验公式无法估算出该变形，从而导致10 mm左右的误差。

(2) 国外工程中运用的经验公式经过修正后计算值与有限元计算结果吻合度较高，其中，垂向变形最大差值为7.18 mm，纵向变形最大差值为4.29 mm，较适合运用到FPSO甲板变形的估算中。

(3) 国内工程估算方法预报精度较高，相较于DNV经验公式与国外的工程估算方法每个模块都需要根据对应剖面的静水弯矩、波浪弯矩等载荷计算模块的相对变形，国内工程估算方法需要的自变量较少，更加能保证计算结果的精确性。