波浪作用下并联三箱间窄缝内流体共振

冉雅晴， 姜胜超*， 耿宝磊

(1. 大连理工大学 运载工程与力学学部 船舶工程学院， 辽宁 大连 116024；2. 交通运输部天津水运工程科学研究院 港口水工建筑技术国家工程实验室 工程泥沙交通行业重点实验室， 天津 300456)

0 引 言

随着海洋资源开发不断向深水和超深水方向发展，浮式液化天然气生产系统(Floating Liquefied Natural Gas System，FLNG)和浮式生产储卸油装置(Floating Production Storage and Offloading，FPSO)等大型海上浮式结构系统越来越受到人们的青睐。在这些大型海上浮式结构系统的作业过程中，通常采用一条或多条穿梭油船与其并联进行油气外输。此时，浮式结构系统与穿梭油船间会出现相对于结构尺度小得多的狭窄缝隙。当入射波浪频率与缝隙间流体自振频率耦合时，缝隙流体会发生强烈的大振幅共振，对结构物作业产生重要影响，这成为多船舶并靠作业过程需要解决的关键问题之一。

针对船舶间窄缝内水体共振问题，国内外学者采用理论研究、模型试验和数值模拟等方法进行多方面的研究。传统的线性势流模型是迄今为止应用最广泛的方法。MIAO等[1]采用渐进匹配法研究带狭缝二维双箱的共振现象，并且给出狭缝很小时双箱的理论共振频率。SAITOH等[2]采用试验方法进行研究，发现窄缝内最大共振波高可达入射波高的5倍。IWATA等[3]将这一问题扩展至三维模型中，并且发现方箱数量也会对共振现象产生影响。KRISTIANSEN等[4]采用数值模拟和试验研究发现，线性和非线性势流数值结果下的箱体与固定式岸壁结构之间窄缝内共振波高都比窄缝内共振试验波高大，特别是线性结果更大，这是由于势流理论使用无黏无旋假设，因此过高地估计方箱间流体共振波高。CHEN[5]将阻尼项引入自由表面边界条件，并将其解释为能量耗散。LU等[6-7]建立黏性流模型和带阻尼的势流模型并计算双箱和三箱体窄缝内的流体共振现象，发现2种模型均能较准确地模拟共振波高和共振频率。

此外，何广华等[8]采用比例边界有限元法发现受狭缝影响3个相同尺度的方箱在比较接近的2个频率处发生共振现象。宁德志等[9]建立二维非线性时域数值波浪水槽模型，分析箱体数量对窄缝内水体共振的影响。苏晓杰等[10]通过数值计算，分析箱体数量对各箱体所受波浪载荷大小和变化规律的影响。宁德志等[11]发现当窄缝内水体发生共振时，作用在箱体上的波浪载荷非线性影响明显，并且作用在迎浪侧结构上的载荷大于背浪侧结构。陈学彬等[12]和JIANG等[13]研究箱体浸没水深对共振的影响。谭雷[14]和MORADI等[15]进一步研究不同底角半径的双箱结构，发现圆角方箱间窄缝共振波高远大于箱体底角为直角的情况。姜胜超等[16]基于OpenFOAM对共振发生时的能量转移和耗散过程进行重点分析。

但是，上述研究大多基于双箱或三箱结构相同的情况。在实际工程中，FLNG或FPSO尺度通常大于液化天然气船或穿梭油船，与此同时，在并靠作业中，不同浮体的布置方式会对多物体系统的水动力性能产生显著影响，从而对海上作业效率产生重要影响，而对这一问题的研究还相对较少。因此，本文在前人研究基础上，对波浪作用下不同吃水并联三箱窄缝内共振进行研究，并在窄缝内引入人工阻尼项以抵消共振时产生的黏性耗散，同时对3种不同布置方式下窄缝共振时的波高、透射系数、反射系数和不同箱体所受到的作用力大小进行分析比对进而得出最佳布置方案，此外，还考虑箱体底角几何形状和箱体吃水大小对三箱系统下窄缝共振特性的影响。

1 数值模型

考虑波浪对固定物体的作用问题，在理想流体且运动无旋假设下，流体运动存在速度势Φ(x,t)，对于不可压缩均质流体，速度势满足拉普拉斯方程，质量守恒可通过如下拉普拉斯方程进行描述：

∇2Φ=0

(1)

为了模拟基于势流模型的窄缝内阻尼力的影响，在动量方程中引入阻尼项：

f=-μ(x)V=-μ(x)∇Φ

(2)

式中：f为阻尼力；μ为人工阻尼系数；V为窄缝内的平均流速。采用波形ζ的一阶近似可得：

(3)

式中：g为重力加速度。

考虑自由水面上的运动条件：

(4)

将式(3)代入式(4)，可得：

(5)

对于谐波运动，与时间相关的部分可以被分离为Φ(x,y,t)=Re[φ(x,y)e-iω t]，其中φ(x,y)为复速度势，ω为圆频率，从而可以得到复速度势满足的自由水面边界条件为

(6)

进一步将复速度势分解为入射势和绕射势，即

φ(x,y)=φi(x,y)+φd(x,y)

(7)

式中：入射势φi(x,y)为

(8)

式中：A为入射波波幅；k为入射波的波数；h为静水深。进而得出散射势满足的边界条件为

(9)

式中：n为物面的单位法向量，以指出流体为正。

取Rankin源作为格林函数：

(10)

式中：x(x,y)为场点；x0(x0,y0)为源点；r=[(x-x0)2+(y-y0)2]1/2；r1=[(x-x0)2+(y+y0-2h)2]1/2。

应用第二格林函数理论，可以得到边界积分方程：

(11)

式中：Sr为波浪水槽两端面积；Sg为窄缝内自由水面面积；Sf为自由水面面积；Sb为结构物表面面积，S=Sf+Sb+Sg+Sr；α为流域内夹角，即为物体表面所占的空间角度。

(12)

式中：Ω为流体计算域;θ为固角。

基于边界积分方程式(11)，使用高阶边界元方法[17]进行离散，即可求出速度势。

2 模型设置与数值验证

数值模型如图1所示，考虑不同吃水和不同底角半径的箱体位于不同位置时波浪与带窄缝箱体系统的相互作用。按照1∶50比例尺进行模型设置，箱体A、B、C放置于静水深h为0.5 m的数值水槽中。

为验证所研究数值模型的准确性，先考虑波浪对2种底角半径的并联双箱的影响。其中，箱体宽度B=0.50 m，窄缝宽度Bg=0.05 m，箱体吃水DA=DB=0.252 m。浪高仪Gp1和Gp2分别放置于2个窄缝处，用于测量窄缝内自由水面波高。将所得数值结果与SAITOH等[2]和谭雷[14]的试验结果进行对比，如图2所示。图2中：Hg/H0为无因次波高；R为底角半径；曲线μ=0.2和μ=0.4代表增加人工阻尼后得到的结果。由图2可知：势流模型结果可准确预测共振频率，但显著高估共振波高；采用增加人工阻尼的方法可有效对共振频率附近的波高进行抑制，数值计算结果与试验结果符合良好，说明所研究方法的准确性。需要说明的是，对于底部为直角和圆角的情况，阻尼因数分别取0.4和0.2时可获得较准确的结果，即圆角情况的阻尼因数小于直角情况。这主要是由于在圆角情况下，流体涡旋运动较弱，从而产生的机械能损耗较小，因而需增加的人工阻尼系数较小。

图2 两箱时窄缝处无因次波高随频率的变化

进一步对并联三箱的情况进行验证，将所得结果与IWATA等[3]的试验结果和LU等[6]的有限元数值结果进行对比。对箱体宽度B=0.50 m，窄缝宽度Bg=0.05 m，箱体吃水DA=DB=DC=0.252 m，底部为直角的情况进行计算，结果如图3所示。图3中，Ag/A0为无因次振幅。由图3可知：在传统势流结果中，当振幅ω为4.90和5.50 rad/s 时2个缝隙的自由水面均出现峰值，其分别为第1共振频率ω1和第2共振频率ω2；在第1窄缝处，传统势流理论高估共振波高；在第2窄缝处，第2共振频率甚至并未出现在试验与黏性流结果中。产生上述结果的主要原因仍然是势流结果忽略了流体黏性。对于直角情况下的三箱模型，当阻尼系数取μ=0.4时，数值模拟结果与试验结果吻合较好，验证所研究方法的可用性。

图3 三箱直角时窄缝处无因次振幅随频率的变化

3 数值结果

为研究不同布置方式对多船舶联合作业的影响，仍如图1所示，对不同吃水深度的并联三箱进行研究，波浪仍从左向右传播，水深h=0.5 m，箱体A、B、C宽度均为B=0.50 m，窄缝宽度Bg=0.050 m，对底部为直角(R=0 cm)和底部为圆角(R=5 cm)两种情况进行考虑，吃水深度取值如表1所示。情形1为大吃水船舶布置于迎浪侧，情形2为大吃水船舶布置于2艘小船中间，情形3为大吃水船舶布置于背浪侧。

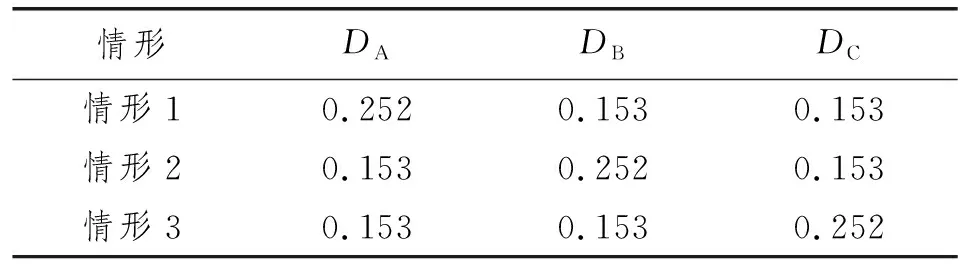
表1 模型参数设置 m

考虑不同布置方式下的三箱系统缝隙内波面变化情况，分别采用传统势流理论(μ=0)与所研究势流模型施加人工阻尼的方法进行计算，结果如图4 所示。由图4可知，在2种底部结构条件下，缝隙内自由水面运动振幅随频率的变化基本一致，但底部圆角情况的共振波高大于底部为直角的情况，且预测的共振频率向高频移动。

图4 不同布置方式下振幅随频率的变化

对比不同布置方式对共振频率的影响，可以看出：情形1与情形3两种布置方式具有相同的共振频率，以底部圆角情况为例，第1与第2共振频率分别为ω1=5.60 rad/s 和ω2=6.90 rad/s；情形2在底部圆角情况下的共振频率为ω1=5.90 rad/s和ω2=6.40 rad/s，两者之间更为接近，即当大吃水船舶布置于中间时，三箱双窄缝系统的共振频率的范围更加集中。对比不同布置方式对共振波高的影响，可以看出：在第1个窄缝处，当大吃水船舶布置于迎浪测时共振波高最小，尤其是入射波浪频率接近第2共振频率附近的情况，情形2布置方式的共振波高最大；在第2个窄缝处，情形1布置方式在2个共振频率附近均具有较小的波高，情形3在第1 共振频率附近波高显著高于其他两组情况。

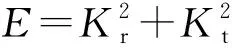
图5 不同布置方式下水动力因数随频率的变化

对不同布置方式下箱体的受力情况进行分析，分别选取大箱体与迎浪侧小箱体所受水平波浪力和垂向波浪力随入射波频率的变化关系进行研究，结果如图6和图7所示。

对比大吃水箱体受到的水平波浪力情况，情形1布置方式下的大吃水箱体受到的水平波浪力最小，上游大吃水箱体对后方箱体的遮蔽使得窄缝内自由表面振幅较小。相反，当大吃水箱体位于中间或后方时，其受到的水平波浪力明显增大，说明在此方案下窄缝内自由水面振幅较大进而使后方大吃水箱体受到较大的水平波浪力。对比大吃水箱体所受到的垂向波浪力情况，由伯努利方程可知，箱体所受到的垂向波浪力主要来自于箱体底部附近的流体速度。情形1方案下大吃水箱体受到的垂向波浪力最小，即上游大吃水箱体遮挡较多波能进而使箱体底部流速较小。相反，由于遮蔽效应减小，在情形2和情形3方案下，最大箱体所受垂向波浪力明显增大。同时发现，在势流理论下情形3的垂向波浪力变化中出现第2共振频率。

图6 不同布置方式下大箱受力随频率的变化

图7 不同布置方式下迎浪侧小箱受力随频率的变化

情形1迎浪侧为大吃水箱体，比较不同位置处的2个小箱体受力，可知B箱和C箱所受水平波浪力大小相近，B箱所受垂向波浪力较大。迎浪侧箱体的最大水平载荷都发生在共振频率附近。由图7(a)可知：受到上游大吃水箱体的遮蔽效应影响，情形1方案下迎浪侧小箱(B箱)受到的水平波浪力最小；在情形2中，中间大吃水箱体的反射效果使得迎浪侧小箱所受水平波浪力最大。由图7(b)可知：最大垂向载荷发生在第一共振频率附近，情形3布置方式下迎浪侧小箱体受到的垂向波浪力最大，情形2时受力略小，情形1中特征频率处迎浪侧小箱体受到的垂向波浪力最小。

综合图4～图7可知：当大箱体放置于上游时，波浪反射较大，导致更多的波能反射，进而导致三箱间窄缝共振波高较小，同时也导致能量耗散更少。同理，由于三箱缝隙间流体共振波高较小，因此箱体的受力均较小。由此可见，在上述过程中，大吃水箱体的遮蔽效应是抑制缝隙内波高的最主要原因，可以获得较小的窄缝波高和波浪力。

4 结 论

采用数值方法对波浪作用下并联三箱的水动力共振问题进行研究。数值结果表明，在2种不同的底部结构条件下，缝隙内自由水面运动振幅随频率的变化基本一致，但底部圆角情况下的共振波高大于底部为直角的情况，且预测的共振频率向高频移动。进一步地，考虑不同布置方式对共振波高的影响，可得当大吃水船舶布置于迎浪测时共振波高最小，尤其在入射波浪频率接近第二共振频率的情况下。由于上游大吃水箱体可以对后方形成良好的遮蔽效应，波能无法进入三箱系统进而使得情形1布置方式的反射系数最大；当大吃水箱体位于中间位置时，窄缝内自由水面振动形成辐射源，从而导致情形2中透射系数较高；对比能量系数可知，由于情形1中窄缝未直接暴露于波浪作用下，因此能量耗散较小，共振频率处的能量系数较大。受上游大吃水箱体的遮蔽效应影响，情形1方式下迎浪侧小箱(B箱)受到的水平波浪力最小，情形1中特征频率处迎浪侧小箱受到的垂向波浪力最小。总之，在比较不同布置方式下窄缝内共振特性时，大吃水箱体的遮蔽效应可获得较小的窄缝波高和波浪力。