基于鲁棒约束的PI控制器参数多目标优化及应用

荆立坤，唐宜强，潘凤萍，吴振龙

（1.华电潍坊发电有限公司，山东潍坊261000；2.华电国际技术服务分公司，济南250014；3.南方电网电力科技股份有限公司，广州510080；4.郑州大学电气工程学院，郑州450001）

0 引言

尽管先进控制理论经历了快速发展，比例-积分（Proportional-Integral，PI）控制器在实际现场应用中仍然发挥着不可替代的作用［1］。最近的文献调查显示，广东省的燃煤机组中超过94%的回路采用PI控制器［2］。PI控制器在一类高级惯性温度控制系统［3］、孤岛混合微电网整流器［4］、典型多变量系统［5］、钻杆系统［6］以及永磁同步电机系统［7］等方面有很好的应用；此外，PI控制器在火电机组协调控制系统［8］、过热汽温系统［9］和脱硝系统［10-12］也有许多成功应用。由此可见，PI控制器未来将在能源、化工系统中继续发挥主导作用。

为了取得满意的控制效果，PI控制器参数的整定与优化得到越来越多的重视，如Skogestad内模控制（Skogestad Internal Model Control，SIMC）法［13］、齐格勒-尼科尔斯（Ziegler-Nicholas，Z-N）法［14］、最大灵敏度（Ms）约束的积分增益优化法（Ms-Constrained Integral Gain Optimization，MIGO）［15］等。此外，许多学者基于不同的优化目标提出了基于概率鲁棒的参数整定方法［16］、基于线性二次调节器的参数整定方法［17］和基于预期动态响应的参数整定方法［18］等。一些优化算法，如遗传算法［19-20］、粒子群算法［21］和量子衍生算法［22］也应用于PI控制器的参数优化。

然而，SIMC法和Z-N法主要考虑跟踪性能，没有考虑抗干扰性能和系统鲁棒性；MIGO法考虑了鲁棒Ms约束的抗干扰整定，但忽略了跟踪性能。上述基于优化算法的参数整定方法均是对单一性能指标进行无约束优化，没有考虑鲁棒约束；其他PI参数整定方法同样不能兼顾系统的鲁棒性、跟踪和抗干扰性能。由于燃煤机组负荷需要大范围波动，PI控制器要有很强的鲁棒性，保证偏离设计工况时仍能取得稳定的控制效果。此外，系统的跟踪性能和抗干扰性能是矛盾的，如何在跟踪性能和抗干扰性能之间进行权衡选择也是一个值得研究的问题。

本文从工程实际出发，提出一种基于鲁棒约束的PI控制器参数多目标优化方法。采取最大灵敏度函数作为鲁棒约束指标，在该约束下同时将闭环系统的跟踪性能与抗干扰性能作为优化目标，采用多目标遗传算法在PI控制器稳定域内对参数进行优化，得到满足鲁棒约束的帕累托（Pareto）最优解集，然后借助水平图法得到优化参数。基于该方法优化的PI控制器参数在潍坊某电厂#3高压加热器中投入应用，进一步验证该方法的有效性。

1 基于多目标遗传算法的PI控制器参数优化

1.1 PI控制器稳定域计算

工业现场使用的PI控制器的传递函数形式为

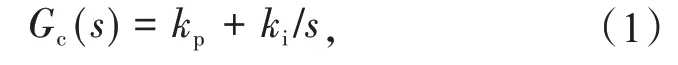
式中：kp，ki分别为PI控制器的比例增益和积分增益。

PI控制器的参数优化必须在参数稳定域内进行，PI控制器的参数稳定域可以采用D-分割法［23］进行计算。

被控对象可以采用如下传递函数进行描述

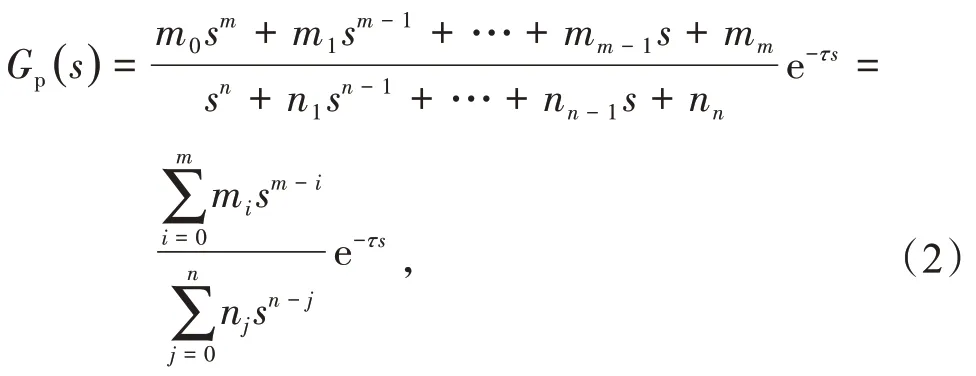
式中：m，n分别为被控对象分子和分母的阶次，m＜n且mm≠0，n0=1；τ为纯滞后时间。

此时被控对象的频域响应为

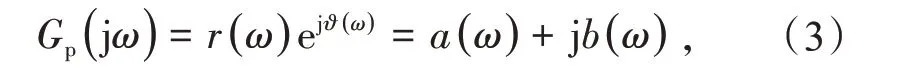
式中：ω为角频率；r(ω)，ϑ(ω)分别为被控对象的幅值和相角；a(ω)，b(ω)分别为被控对象的实部和虚部。

类似的，PI控制器的频域响应为

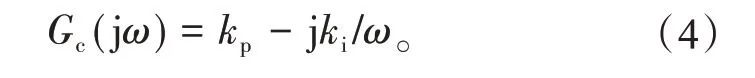
此时，PI控制器和被控对象组成图1所示的闭环系统，图中：R(s)，D(s)，Y(s)分别为设定值、输入扰动和输出的传递函数。

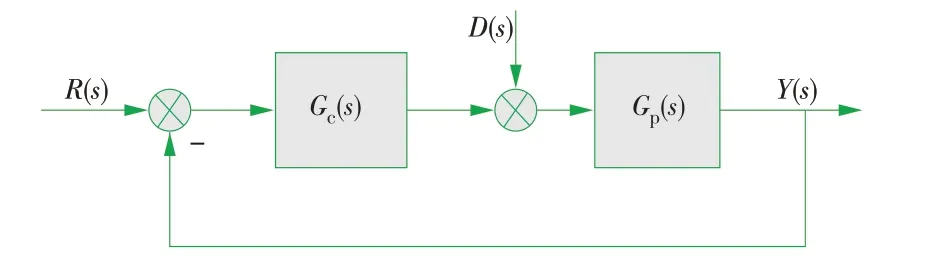
图1 由PI控制器和被控对象组成的闭环系统Fig.1 Closed loop system consisted of a PIcontroller and controlled objectives

基于闭环系统的传递函数可以得到闭环系统的特征方程

即

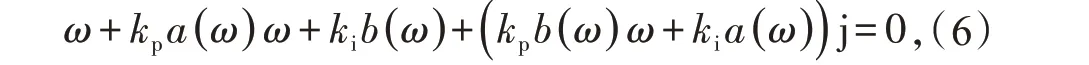
式中：a(ω)，b(ω)为被控对象的特性。

接下来采用D-分割法求解PI控制器的稳定域。根据D-分割法的基本原理，PI控制器的稳定域边界包含ω∈(0，-∞)∪(0，+∞)时的非奇异值边界∂Dω和ω=0，ω=±∞时的奇异值边界∂D0和∂D∞。

（1）ω=0时的奇异值边界∂D0为

由于a(ω)和b(ω)为被控对象的特性，故可知PI控制器的奇异值边界∂D0为ki=0。需要说明的是，纯滞后对PI控制器的ω=0奇异值边界∂D0没有影响（e0=1）。

（2）ω=±∞时的奇异值边界∂D∞与PI控制器没有关系，故PI控制器的ω=±∞奇异值边界∂D∞不存在。

（3）ω∈(0，-∞)∪(0，+∞)时PI控制器的非奇异值边界∂Dω可以通过使式（6）的实部和虚部分别为零来求解，即边界值为

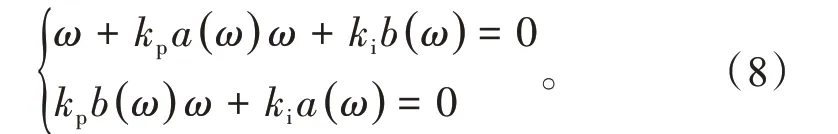
此时，PI控制器参数稳定域为

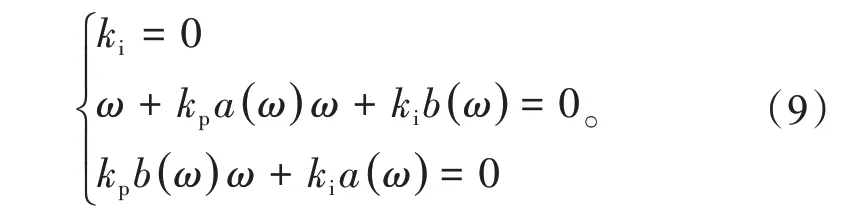
1.2 最大灵敏度函数约束

常用的鲁棒指标可以由图2表示，即Ms约束可以描述为开环系统Nyquist曲线上的点到（-1，0j）点最近距离的倒数，图2中A点到（-1，0j）距离的倒数即为Ms。

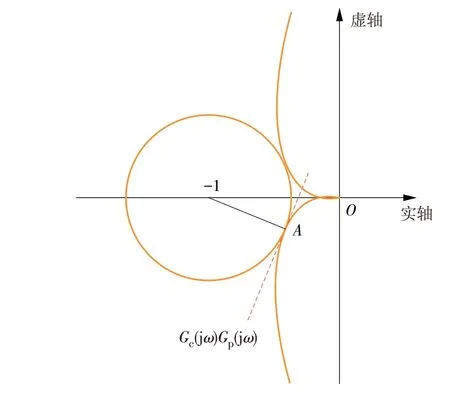
图2 灵敏度约束的几何表示Fig.2 Geometry of sensitivity constraints

Ms可以描述为

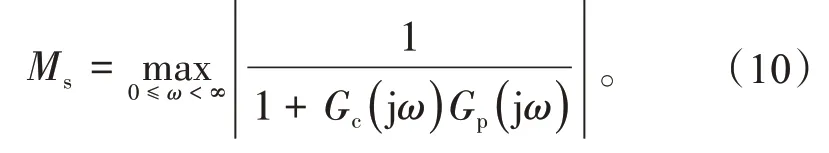
Ms值越小，说明闭环系统的鲁棒性越强，反之亦然。Ms合理值一般在1.2～2.0之间［24］。

PI控制器需要兼顾闭环系统的动态性能和鲁棒性能，因此PI控制器参数应在满足鲁棒约束的条件下进行优化。

1.3 多目标遗传算法

多目标遗传算法能够对多个冲突的目标同时进行优化，得到多目标优化问题的Pareto最优解集（如图3所示），从而帮助决策者挑选出合适的Pareto解。本文采用在带有精英策略的快速非支配排序遗传算法（Non-dominated Sorting Genetic AlgorithmⅡ，NSGA-Ⅱ）基础上开发的NSGA-Ⅲ多目标遗传算法［25］，其特点是在NSGA-Ⅱ的基础上引入参考点机制，保留那些非支配且接近参考点的种群个体，具有良好的搜索Pareto最优解集的能力。

由于闭环系统的跟踪性能与抗干扰性能是矛盾的，为了在保证系统鲁棒性的前提下得到兼顾跟踪性能与抗干扰性能的控制器参数，将跟踪性能与抗干扰性能作为2个优化目标。采用误差绝对值积分（Integrated Absolute Error，IAE）作为性能指标，其数学定义为

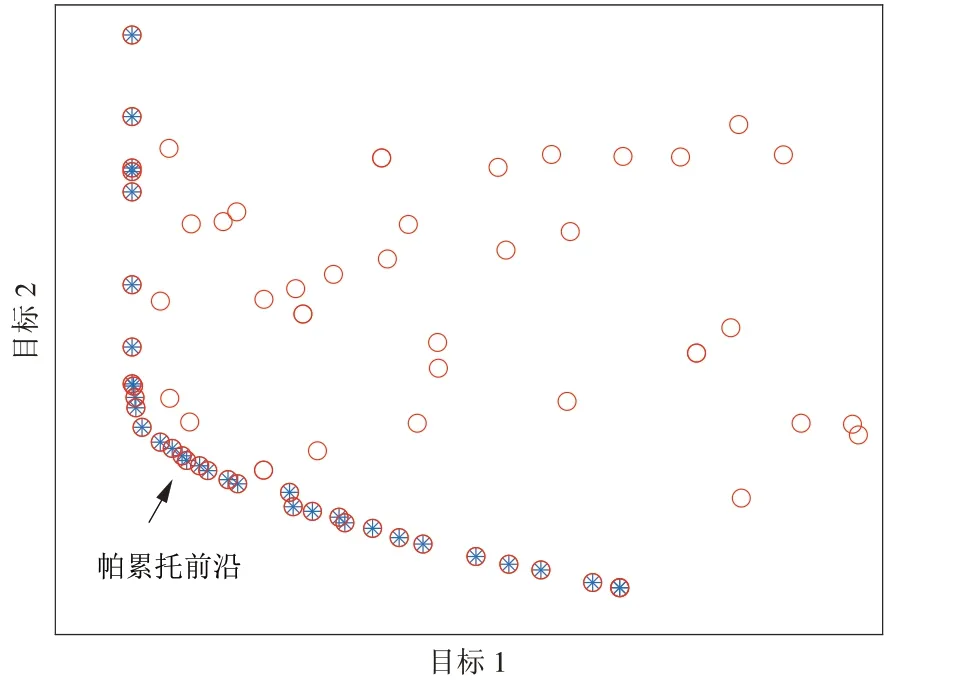
图3 Pareto最优解Fig.3 Pareto optimal solution

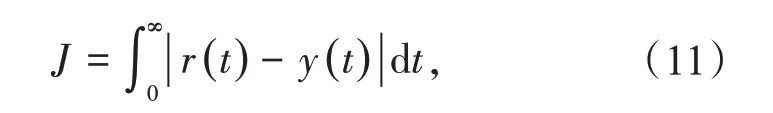
式中：r（t），y（t）分别为闭环系统的输入和输出信号。

采用Jsp和Jid表示设定值跟踪性能与抗干扰性能指标，此时基于鲁棒约束的多目标PI控制器参数优化问题可以转为如下优化问题

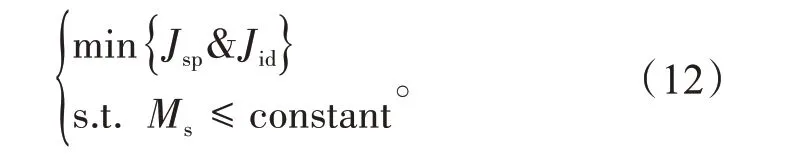
2 仿真验证

2.1 参数整定流程

基于鲁棒约束的PI控制器参数多目标优化方法可以通过以下步骤实施（如图4所示）。

（1）基于已知的被控对象的模型信息，计算PI控制器的参数稳定域，作为NSGA-Ⅲ的初始种群。

（2）采用NSGA-Ⅲ对种群内个体进行优化，通过非支配分层和从最后一个非支配层级中挑选个体进入子代，迭代一定代数后得到Pareto最优解集。

（3）采用水平图法得到优化后的PI控制器参数。

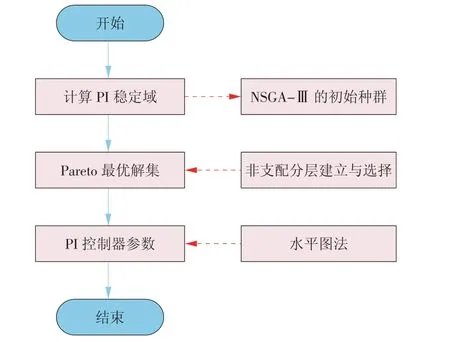
图4 参数优化流程Fig.4 Optimizing process of the parameters

2.2 仿真验证

基于潍坊某电厂#3高压加热器的运行数据，可以得到高压加热器水位的传递函数为

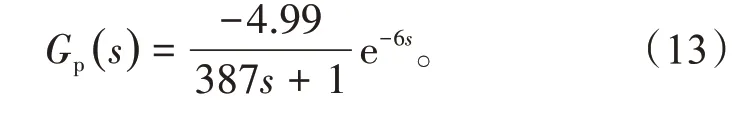
根据式（9）可得到划线区域的稳定域（如图5所示），从图5可知，PI控制器参数稳定域范围很大。

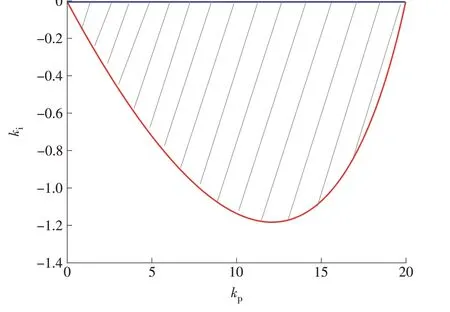
图5 PI控制器参数稳定域Fig.5 Stableregion of PIcontroller parameters

从图5中的稳定域内任取数组PI控制器参数（参数1：kp=5.000，ki=0.400；参数2：kp=0.696，ki=0.122；参数3：kp=10.000，ki=0.200；参数4：kp=8.000，ki=0.800），可以得到图6所示的闭环系统输出，仿真中设定值在10 s时有一个幅值为1的阶跃，输入扰动在600 s时有一个幅值为1的阶跃。

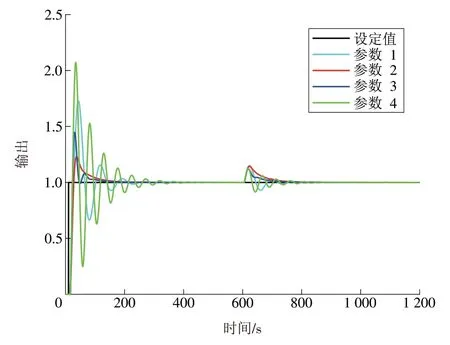
图6 稳定域内PI参数的系统输出Fig.6 System outputs of PI parameters in stable regions

从图6可知，稳定域内参数保证闭环系统在进行设定值阶跃和输入扰动时均可以到达系统的稳态。然而，任取的PI控制器参数导致系统存在超调较大、抖动严重和抗干扰能力不足等问题，因此需要对稳定域内参数进行优化。

按照上节的参数优化流程，通过选择式（12）中不同的鲁棒性约束指标Ms，可以得到图7所示的结果。从图7可知，随着鲁棒性的增强即Ms的减小，Pareto最优解的值逐渐增大，说明在不同的鲁棒性约束下，优化后的控制效果有很大差异，因此，选择合适的鲁棒性约束指标十分重要。

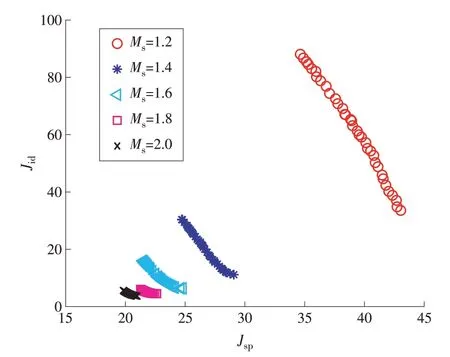
图7 不同M s约束下的Pareto最优解Fig.7 Pareto optimal solution under different M s constraints

通过调阅现场分散控制系统（Distributed Control System，DCS）数据可知，现场使用的控制器参数为kp=-0.45，ki=-1/90，计算可知鲁棒指标Ms=1.74。为保证鲁棒约束一致，选取Ms=1.74作为鲁棒约束指标，采用上节的参数优化流程可得到图8所示的Pareto最优解。由图8可知跟踪性能与抗干扰性能是矛盾的，采用水平图法进行决策［26］。

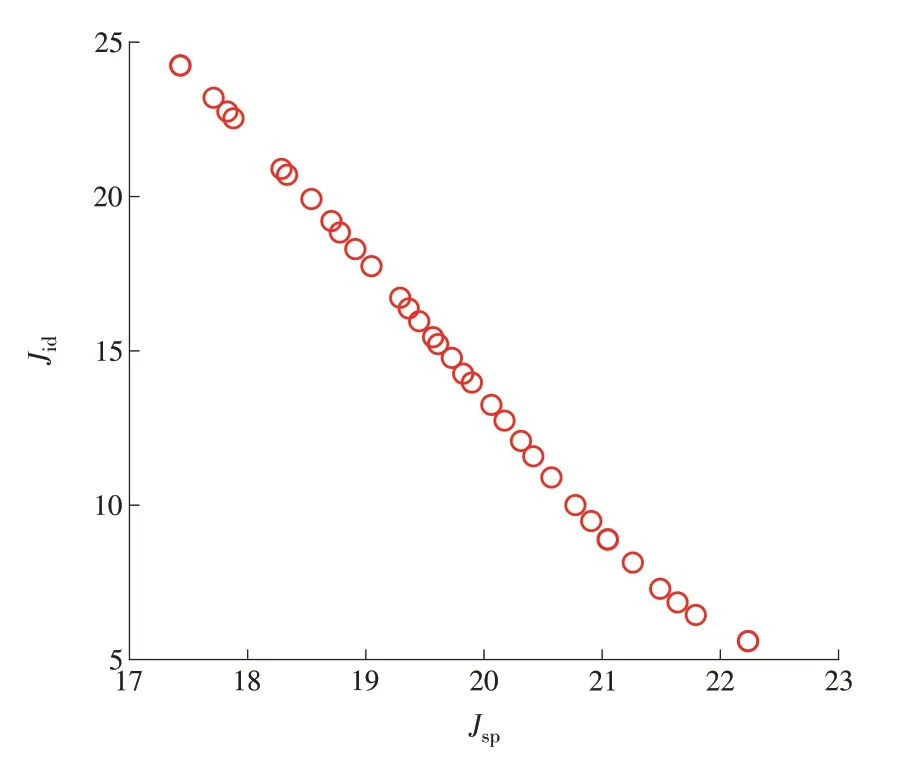
图8 M s=1.74时的Pareto最优解Fig.8 Pareto optimal solution with M s=1.74

||J（θ）||2表示水平图法的y轴衡量基准，可以得到图9所示的结果。由图9可以看出，优化目标Jsp和Jid具有相反的趋势，即Jsp减小的同时Jid增大。将图8中Pareto最优解对应的2个待优化参数的集合采用相同方法进行可视化处理，如图10所示。从图10可以看出，kp和ki随着决策点位置的移动具有相同的趋势，选择||J（θ）||2=0.40时的动态参数（图9和图10中的黑色五角星），此时决策最优解下的动态参数kp=-6.964 0，ki=-0.122 8。

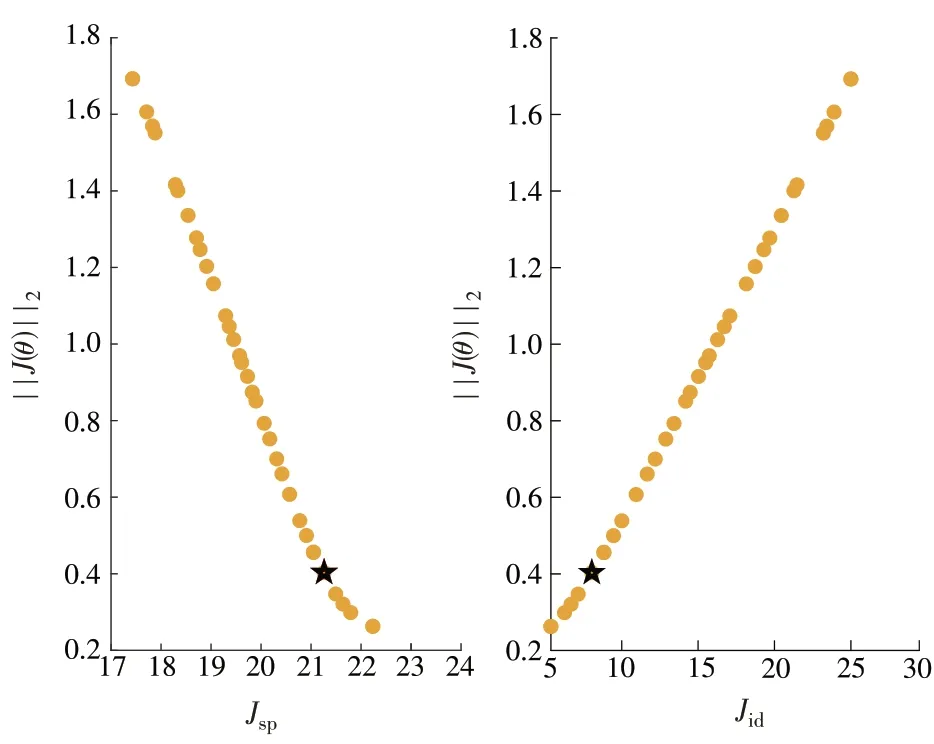
图9 基于||J（θ）||2的Pareto解集Fig.9 Pareto solution set based on||J（θ）||2

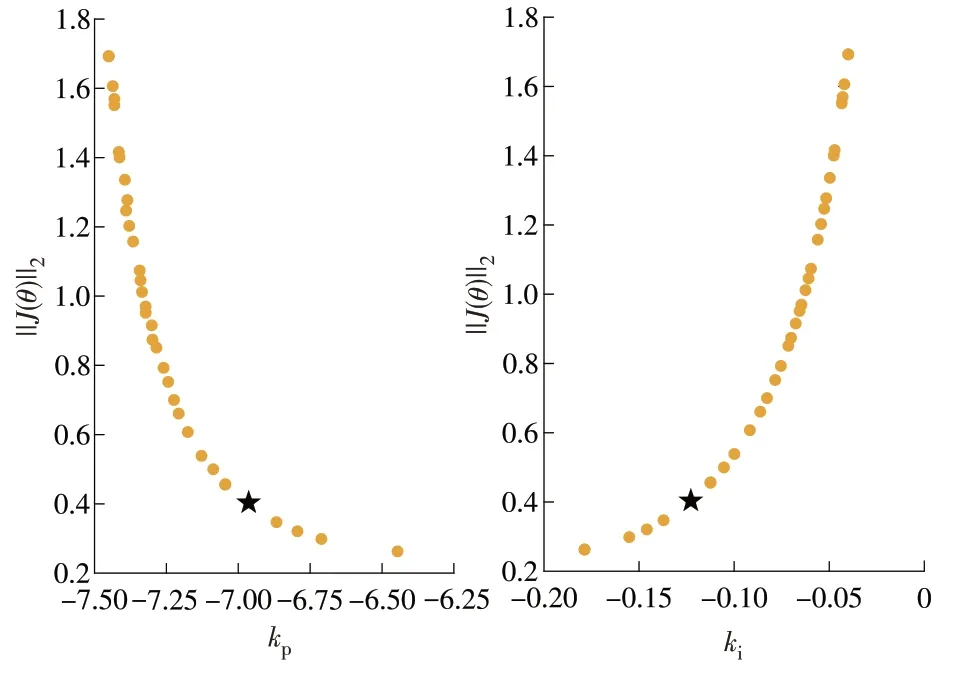
图10 基于||J（θ）||2的参数集Fig.10 Pareto set based on||J（θ）||2

作为对比，采用文献［13］，［15］提出的SIMC和MIGO对式（13）中的高压加热器水位系统进行整定，可以得到PI控制器参数分别为：kp=-5.8750，ki=-0.1113（SIMC）；kp=-4.360 0，ki=-1/67.7710（MIGO）。结合现场应用的PI控制器，可以得到图11所示的控制效果，从图11可知：现场参数具有较大的输出波动，控制效果较差；MIGO虽然超调较小，但抗干扰能力较弱，在扰动发生时需要较长的时间才能达到系统稳定；SIMC的控制效果与本文优化参数比较接近，但本文优化参数在抗干扰性能和跟踪性能方面相比于SIMC有一定优势。表1为各个控制器的性能指标Jsp和Jid的统计值，表中数据可以进一步验证上述分析结果。

为了进一步分析系统存在不确定性时控制器的控制效果，假设式（13）中传递函数的增益、时间常数和滞后常数均变为原来的0.8倍，在保持控制器参数不变的前提下可以得到图12所示的控制效果。从图12可知，本文优化参数仍然具有最好的跟踪性能和抗干扰性能，说明了本文方法的有效性，为现场的应用提供了支撑。

图11 标称系统的输出Fig.11 Outputsof thenominal system

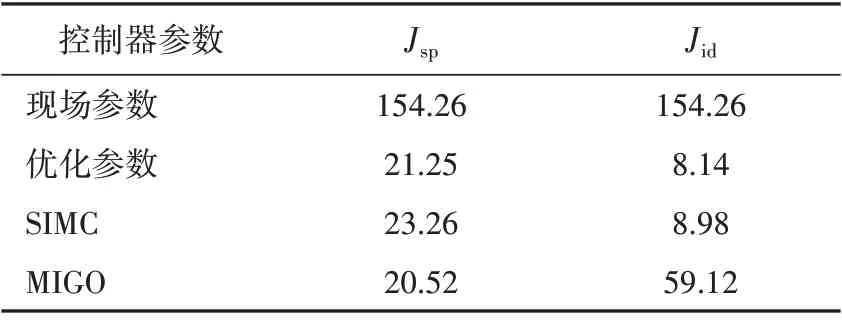
表1 标称系统性能指标统计Tab.1 Performance indexes of the nominal system

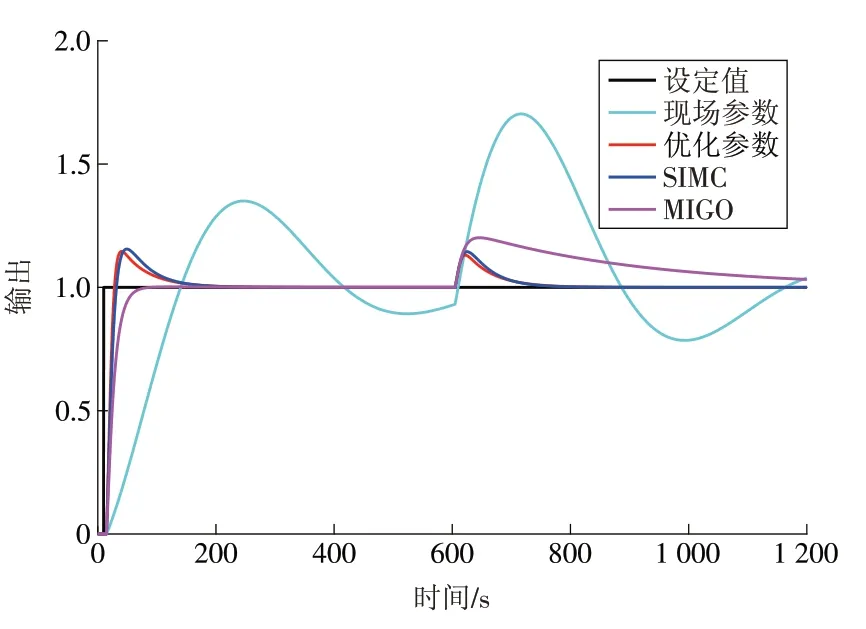
图12 非标称系统的输出Fig.12 Outputs of the non-nominal system

考虑极端工况，即被控对象的结构存在不确定性，因此假设式（13）中被控对象变成了如下对象

在保持控制器参数不变的前提下可以得到图13所示的控制效果。从图13可知，尽管超调量大于MIGO，但本文优化参数仍然具有最好的跟踪性能和抗干扰性能。

综合图11—13可知，本文所提方法不仅能够保证系统在标称工况下的控制性能，当系统参数不确定和结构不确定时仍能够保证理想的控制效果。

为了分析本文所提方法所能容忍系统时滞和增益系数的变化范围，采用Nyquist判据方法探究时滞和增益系数的边界范围。不同时滞和增益系数变化时的开环Nyquist结果分别如图14和图15所示。

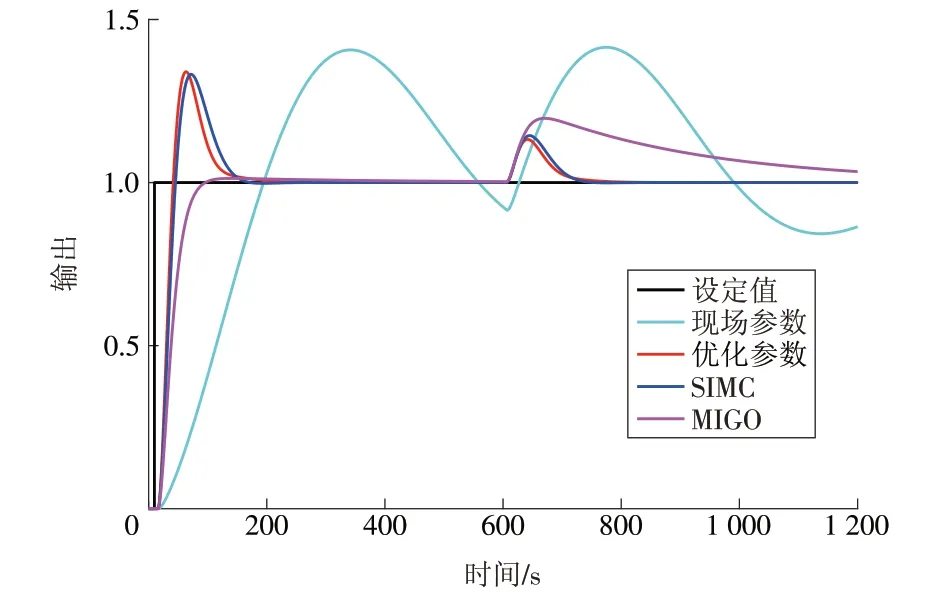
图13 考虑结构不确定时非标称系统的输出Fig.13 Outputsof thenon-nominal system with structural uncertainty

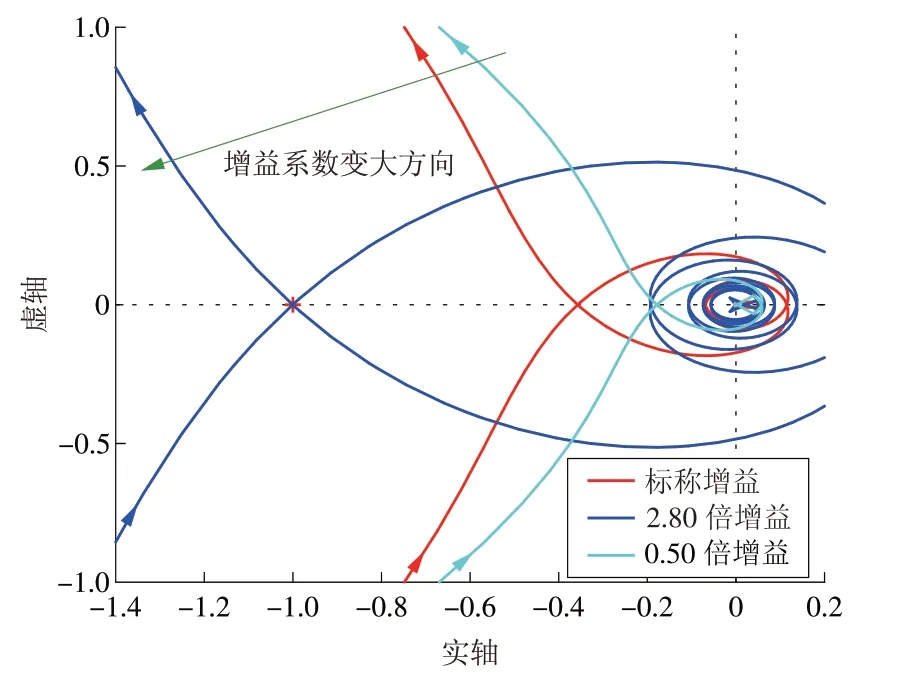
图15 增益系数变化时的Nyquist结果Fig.15 Nyquist resultswith varying gain coefficients

从图14可知，时滞减小能够提高系统的稳定性，随着时滞的增加系统稳定性下降，直到系统不稳定，本文方法所能容忍系统时滞为标称时滞的0～2.57倍。从图15可知，增益系数减小能够提高系统的稳定性，随着增益系数的增加系统稳定性下降，直到系统不稳定，本文方法所能容忍系统增益系数为标称增益系数的0～2.80倍。说明本文所提方法能够容忍系统时滞和增益系数存在较大的变化，具有较强的鲁棒性。当时滞和增益系数变化超出该范围时，必须重新整定PI控制器参数才能保证满意的控制效果。

3 高温高压加热器的现场应用

将优化参数投入该厂#3高压加热器的PI控制器中，得到优化参数投入前、后的水位波动情况，如图16、图17所示。需要说明的是，投入前、后的负荷波动范围分别为212.1～257.6 MW和208.1～280.9 MW，这意味着优化参数经历了更大的负荷扰动。

从图16—17及表2可知：尽管经历了更大的负荷扰动，优化参数下的水位波动范围只有现场参数的61.89%；偏差绝对均值和方差也表明优化参数具有明显优势；优化参数下的阀门开度较现场参数下的阀门开度更加平滑。此外，如果采用工控机，通过合适的工具包，结合闭环辨识方法，能够实现PI控制器参数的在线整定。

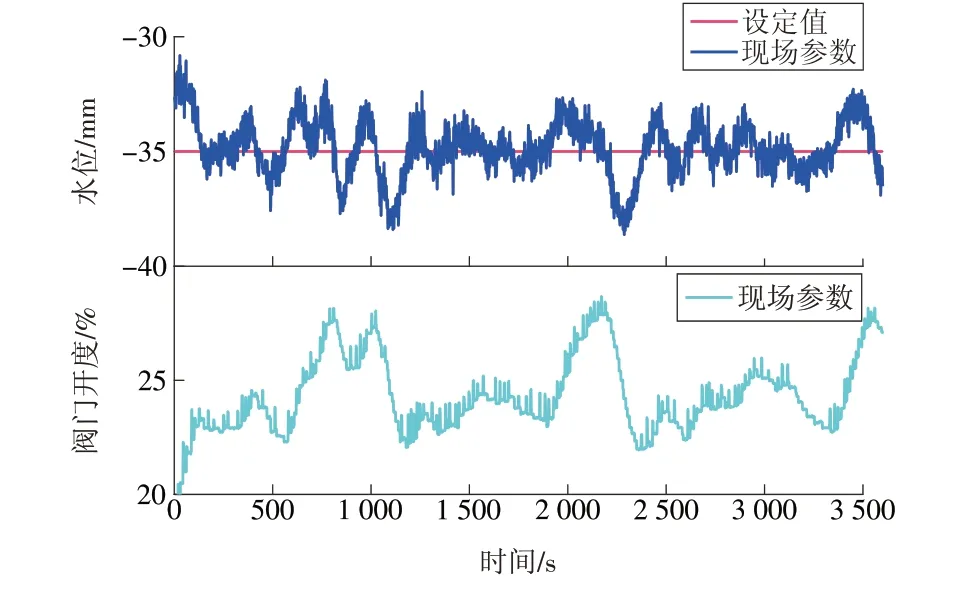
图16 现场参数下的水位波动及阀门开度Fig.16 Water level fluctuation and valveopening with field data

?

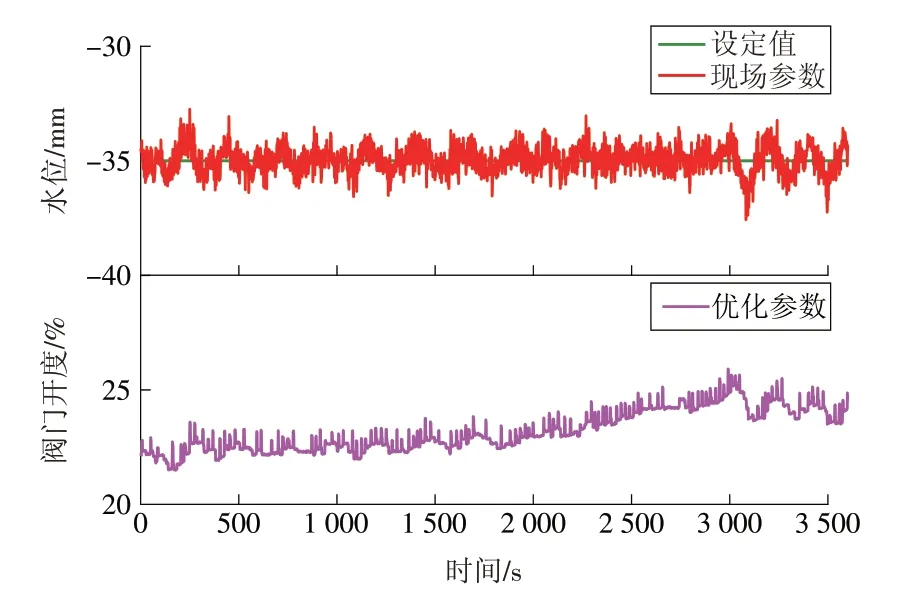
图17 优化参数下的水位波动及阀门开度Fig.17 Water level fluctuation and valveopening with optimized parameters

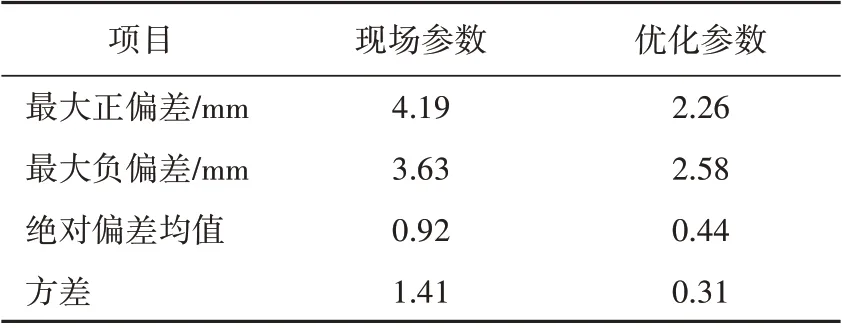
表2 高压加热器水位运行数据统计Tab.2 Statistics of high-pressureheater water levels

4 结束语

为提升系统运行品质，本文提出了一种基于鲁棒约束的PI控制器参数多目标优化方法。采取最大灵敏度函数作为鲁棒性能指标，在该约束下将闭环系统的跟踪性能与抗干扰性能同时作为优化目标，采用多目标遗传算法在PI控制器稳定域内对参数进行优化，得到满足鲁棒约束的Pareto最优解集，借助水平图法得到优化参数。与SIMC和MIGO等经典整定的参数以及现场参数的仿真对比表明，该优化方法具有最优的控制效果。采用该方法优化后的PI控制器参数在潍坊某电厂#3高压加热器中投入应用，更大的负荷波动范围内高压加热器水位波动范围只有原来的61.89%。