基于卷积神经网络的机舱风速修正

杨明明

（华润电力技术研究院有限公司，广东深圳，518002）

0 引言

截至2019年年底，全球风电累计装机容量达到650 GW，其中中国装机容量210 GW，占全球总装机容量的32.3%。针对风电机组性能评估、降载控制、精准偏航等方向的研究显得尤为重要［1-2］。

风电机组的机舱风速计位于机舱尾部，其受到风机尾流和叶片扰动的影响，造成机舱风速与真实来流风速存在偏差。这种偏差的存在影响了机组控制策略的效能和发电性能。为消除偏差，一般在风机前侧设立测风塔或者激光雷达进行实时来流风速测量。但如果采用该办法覆盖全场机组，建设难度和成本都较大。因此，通过数理模型建立机舱风速和真实来流风速的传递关系成为研究重点［3-5］

目前，国内外对机舱风速传递关系的研究也取得了一定的进展，GB/T 33225—2016《风力发电机组基于机舱风速计法的功率特性测试》标准给出了多段折线函数法，通过对风速进行分区，每个区间的线性差值函数构成完整多段折线函数［6］。刘永前等［7］利用风轮单元流管的物理模型仿真机舱前的自由流风速，但风电场运行环境复杂，理论模型结果与实际情况存在较大偏差。张新房等［8］构建了基于支持向量机的自由流风速计算模型，把机器学习引入了机舱传递函数的计算。

由于机舱风速计受到叶片扰动的影响，国际电工委员会（IEC）提出的机舱传递函数（以下简称IEC机舱传递函数）无法准确描述机舱实测风速与来流风速的复杂关系。本研究提出了基于卷积神经网络的机舱风速修正方法，与IEC机舱传递函数相比，多层一维卷积神经网络可有效过滤风电机组尾流和叶片扰动对机舱风速的周期性影响，提高拟合精度，建立一种更为准确的机舱风速修正方法。

1 分析方法与数据

1.1 卷积神经网络

分析采用的一维卷积神经网络［9-10］为包含卷积计算的前馈神经网络，结构分为输入层、卷积层、池化层、卷积与池化层、全连接层5层，如图1所示。

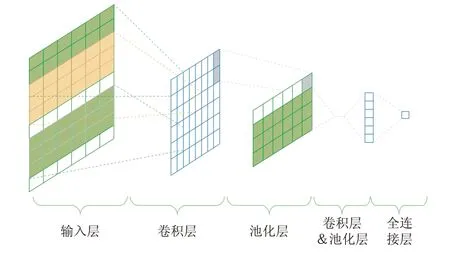
图1 一维卷积神经网络结构Fig.1 One-dimensional convolution neural network structure

假设第l层是卷积层，则一维卷积层的公式为

1.2 监测数据

试验数据来自某风电场25台WTG2000-104机组2018年11月—2019年10月数据采集与监视控制（SCADA）系统间隔为10 min的平均风速、风向、桨距角、发电机转速和功率，以及2019年4月20日—7月14日激光雷达在80 m高度、间隔10 min测得的平均风速、风向。

2 工程实例

2.1 工程概况

某平原风电场，主要植被为低矮农作物和杂草等，主风向位于45°～180°，测试期间以南风为主。激光雷达位于测试机位东南侧250 m处，相对位置如图2所示。

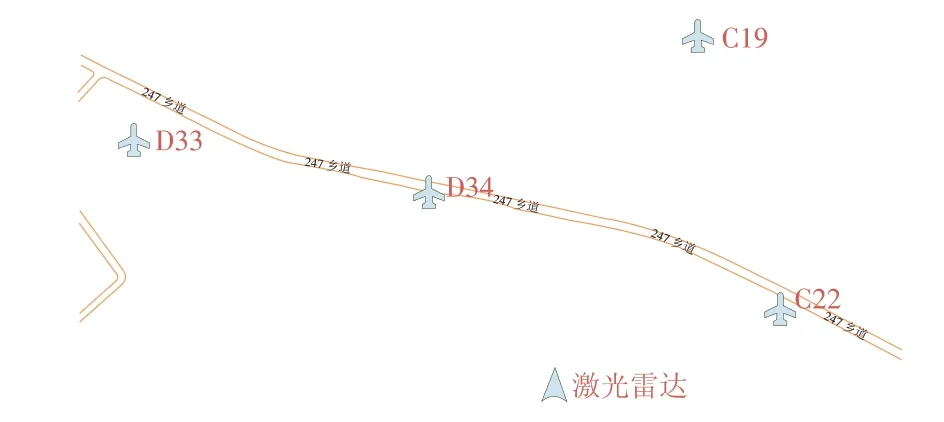
图2 激光雷达与风电机组相对位置Fig.2 Relative positions of laser radars and wind turbines

根据IEC 61400-12-2《基于机舱风速计的风电机组功率特性测试》标准对试验机位进行地形评估，对描述场地地形复杂性的陡峭指数（RIX）和倾角进行计算。D34测试机组地形参数见表1，为地形分类中的1类地形，RIX未超过0.04，地形倾角符合IEC 61400-12-2标准附录B，符合噪声传递函数（NTF）计算和传统功率曲线测试的地形要求。

表1 D34测试机组地形参数Tab.1 Terrain parameters of the test unit D34

根据IEC 61400-12-2标准附录A对测试机组障碍物进行评估，该风场内主要障碍物为风电机组，计算出测试机组D34有效扇区为0°～100°，300°～350°，根据筛选出的有效扇区进行数据分析计算。

2.2 数据清洗

对D34风电机组2019年4月20日—7月14日的10 min间隔平均风速和功率进行数据筛选。由图3可见，切入风速以上有部分功率为0的停机数据，还有部分离散点为风机在切入风速以上遇到异常状况停机过程，以及切入风速以上启动过程中发电机低于正常运行转速所输出的欠功率点。这部分数据会影响机舱风速与激光雷达的函数拟合关系，为提高分析结果的可靠性，对上述数据点位进行剔除［9-10］，剔除后的功率散点图如图4所示。

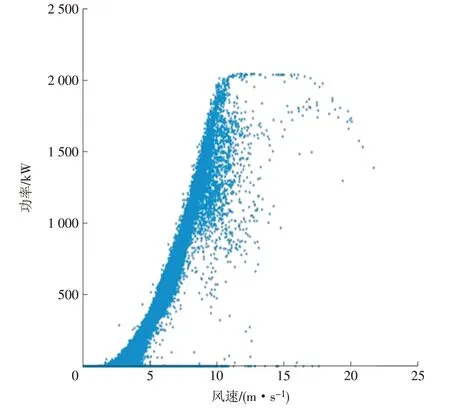
图3 数据筛选前的功率曲线散点Fig.3 Scatter plot of the power curve before data filtering

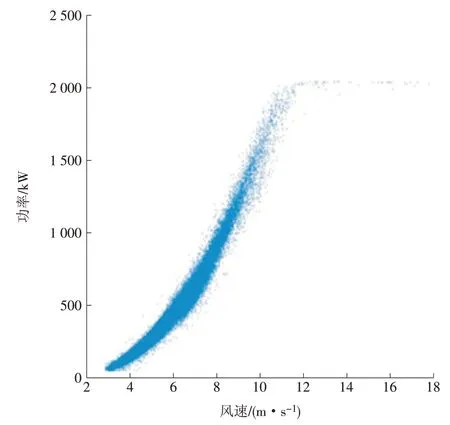
图4 数据筛选后的功率曲线散点Fig.4 Scatter plot of the power curve after data filtering

2.3 卷积神经网络模型

采用Keras的一维卷积神经网络Conv1D函数搭建训练模型。考虑到多层卷积池化可提升网络性能，模型的结构如图5所示，可见模型采用5个一维卷积和池化层，3个全连接层，激活函数为ReLU。同时为避免过拟合，使用了2个Dropout（代表神经网络单元随机丢失）层。模型训练采用的损失函数为均方误差（MSE），优化算法为Adam，学习率设置为0.001。模型输入数据为测试机组SCADA系统10 min间隔的机舱风速、风向、桨距角、发电机转速和发电机功率，训练集和测试集按8∶2的比例随机划分，训练次数（Epochs）为500。

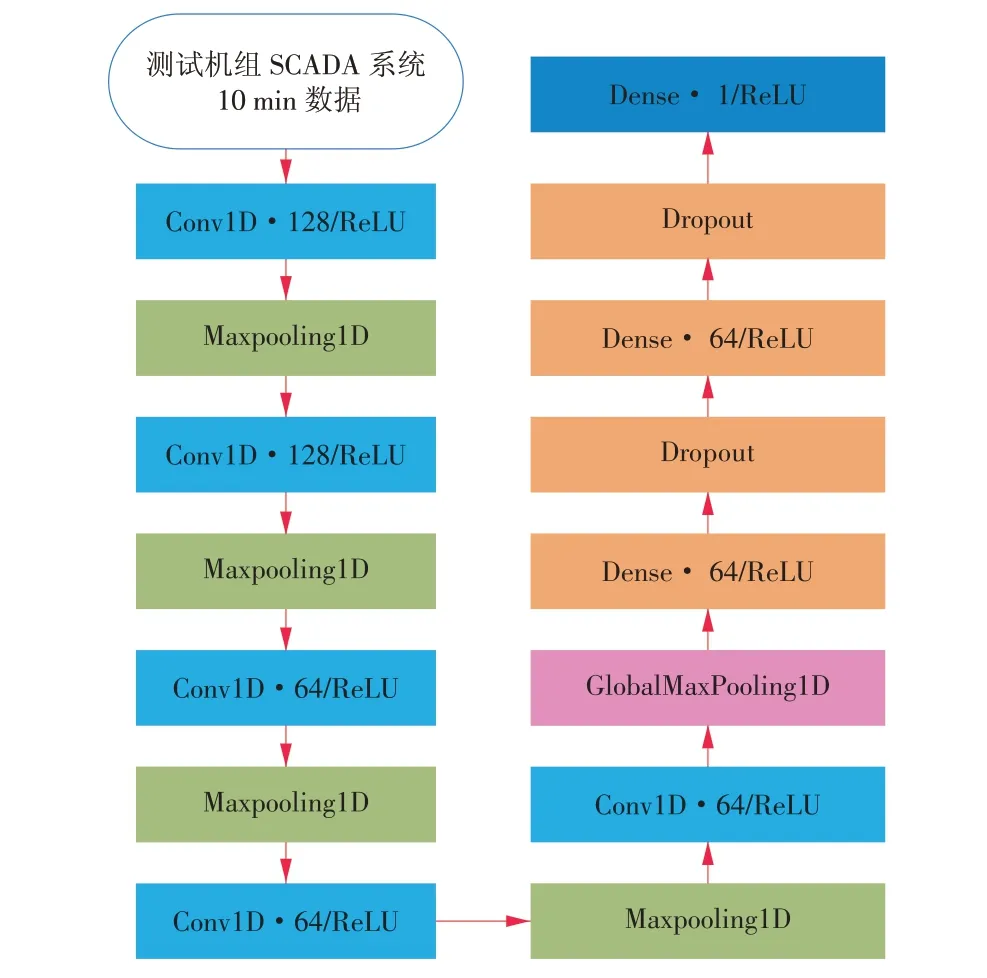
图5 基于卷积神经网络的模型结构Fig.5 Structure of themodel based on convolutional neural network

2.4 实例结果分析

利用测试机组SCADA系统10 min的机舱风速、风向、桨距角、发电机转速和发电机功率的训练集数据进行模型训练，根据训练后得到的权重和偏置对测试集的机舱修正风速进行计算，计算结果与实测风速的误差分布以及相关性如图6所示。从图中可以看出计入误差分布集中，主要分布在0值附近，并且计算值与实测值相关性较好。

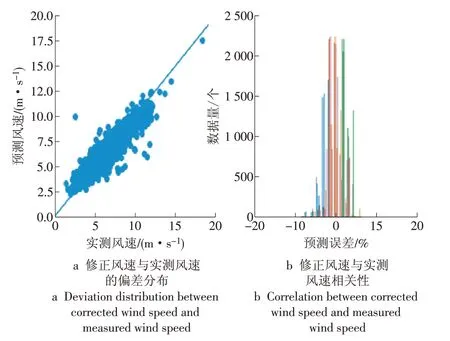
图6 修正风速与实测风速的偏差分布及相关性Fig.6 Deviation distribution and correlation between corrected wind speed and measured wind speed

利用同一数据集进行IEC机舱传递函数修正风速的计算，其修正风速和卷积神经网络修正风速与实测风速的拟合关系如图7及图8所示。

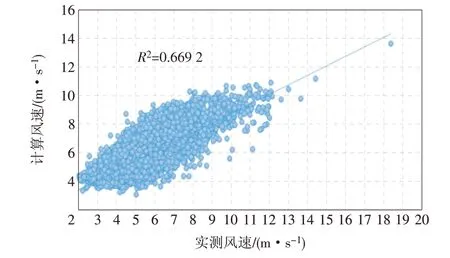
图7 实测值与IEC机舱传递函数法计算值相关性Fig.7 Correlation between measured valueand thevalue calculated by IEC nacelletransfer function

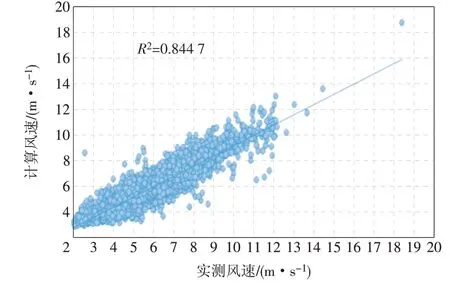
图8 实测值与卷积神经网络法计算值相关性Fig.8 Correlation between measured valueand thevalue calculated by convolution neural network method

表2为IEC机舱传递函数法与卷积神经网络法计算结果比较，由表可见，卷积神经网络法拟合优度较IEC机舱传递函数有较大的提升，同时回归平方和（ESS）的算术平方根及平均绝对误差（MAE）显著小于IEC机舱传递函数［11-14］。

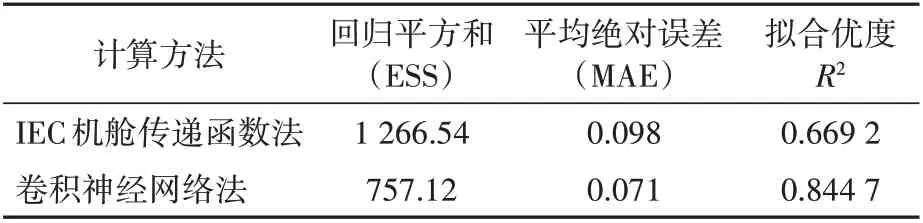
表2 2种计算方法结果比较Tab.2 Comparison of two calculation methods

利用计算所得修正风速和同期功率，采用IEC的Bin法绘制机组功率曲线对比如图9所示，由图可见卷积神经网络法计算的功率曲线与实测功率曲线各风速段的拟合度较好，而IEC机舱传递函数计算的功率曲线在8～12 m/s风速段与实测功率曲线相比偏高，高估了风机性能［15-16］。根据场区测风塔风频，对机舱修正风速的功率曲线和测试功率曲线进行的电量评估，评估电量误差见表3。

由表3可见，在工程实例中，IEC机舱传递函数法绘制的功率曲线评估电量较测试功率曲线偏高5.79%，而卷积神经网络的评估电量偏差仅4.07%，表明在相同的试验条件下，卷积神经网络可以有效提高机舱修正风速的精度［17-19］。

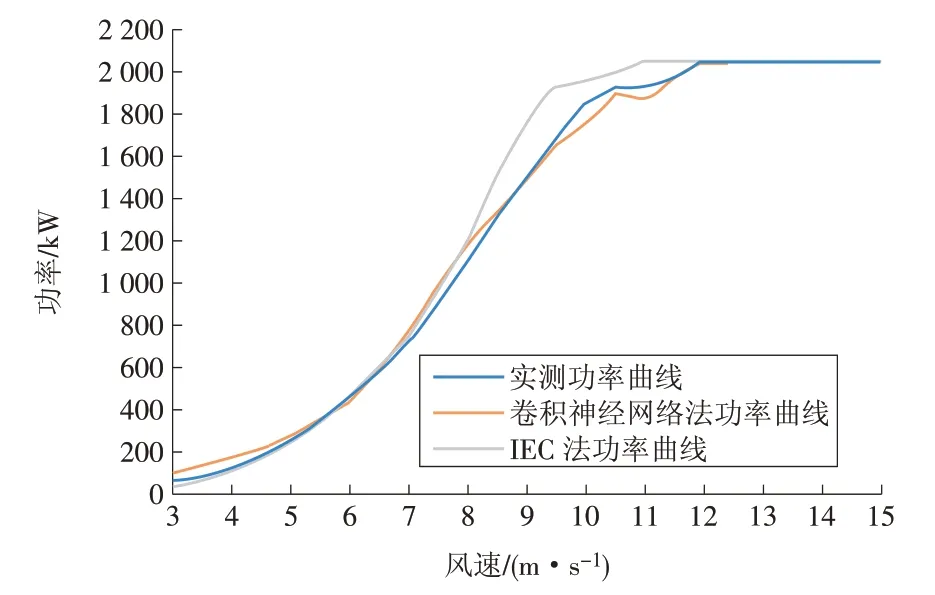
图9 功率曲线对比Fig.9 Power curvecomparison

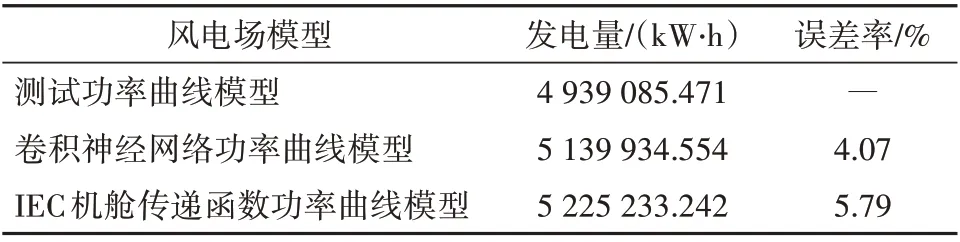
表3 计算功率曲线与测试功率曲线发电量对比结果Tab.3 Comparison resultsof power generation between calculated power curveand test power curve

3 结束语

提出了一种全新的基于卷积神经网络的机舱风速修正方法，可应用于同类型机组的机舱风速功率曲线计算。该方法的核心创新在于能有效过滤了风机尾流和叶片扰动对机舱风速的影响，提高修正风速的计算精度。工程实例表明，卷积神经网络法计算的修正风速与实测风速的拟合优度R2达到0.844 7，MAE仅为0.071，各项偏差指标相较于IEC机舱传递函数分区分段法均有较大提升。基于卷积神经网络法计算的功率曲线与实测功率曲线的评估电量差异仅为4.07%，较IEC机舱传递函数分区分段法提高了1.72百分点。

值得注意的是，机舱风速与自由流风速的关系受场地地形、机组叶轮形状等因素影响，不同条件下测试结果会有所差异。今后将对更多不同类型的场址和机组进行试验，以检验该方法的普适性。