基于进攻关键区域的RoboCup2D球队防守策略的优化*
程泽凯, 管博伦, 郭志浩, 秦 峰
(安徽工业大学 计算机科学与技术学院,安徽 马鞍山 243002)
0 引 言
伴随着人工智能的兴起,许多学者对人工智能应用算法的研究也越来越深入,而RoboCup仿真2D作为一个研究多智能体系统相关技术的平台也被国内外更多的专家学者所关注。RoboCup仿真2D使用的是计算机仿真的2D虚拟机器人,一个虚拟机器人是一个足球队员球智能体,他们是一个独立的个体,表现为一个独立的Client[1]。两个队伍之间比赛的执行采用的是C/S模式,每一个Client与Server之间通过UDP/IP协议进行信息交互[2]。
在多智能体系统的RoboCup仿真比赛中,智能体之间的协作进攻策略是十分重要的,因此很多专家学者对其进行了研究。文献[3]总结了世界杯前3名的球队的特点并且结合2014年的世界杯的战况提出了球员的跑位与比赛的胜负有着很大的关系的结论,其采用了因子分析的方法,通过对日志文件的分析,得到了球员在进攻跑位时的频繁项集,为球员建立了跑位画像,但是其在研究球员跑位时球场仍然按照底层的形式划分,缺乏一定的针对性。文献[4]围绕进攻是足球比赛的关键,提取了关键球员进攻行为数据,对比人类足球提出了更加准确的进攻行为判定方法,检验了“单独进攻”和“合作进攻”两种进攻模式的存在性。文献[5]为了预测球员的跑位建立更好的防守,将球场划分为60个区域,通过球和球员的位置建立搜索树,利用搜索树对球员的进攻跑位区域进行了预测,但是球场的分区是基与传统形式缺乏灵活性。文献[6]通过对日志文件的处理提取了踢球(以下简称kick)数据,并且对不同队伍的kick数据进行了相似性分析,找到了不同球队策略的差异。其他的球队也做多相似研究。
上述文献的研究普遍侧重于球员进攻时的跑位,对球场按照底层或者传统的方法进行划分,来寻找球队的进攻策略,然而在进攻时涉及的球员较多、跑位离散度往往比较大,基于基层或者传统的球场划分不能很好地表现每支球队的特点,而且还受到阵型等因素影响[7],得到的结果往往不准确。
现以足球为主导因素,通过对比赛日志文件的分析解释了球队在进攻过程中侧重点存在的合理性,首先参照球队进攻时球的位置分布的特点对球场进行了动态的离散划分,其次利用自适应密度聚类算法在球场离散后的每一个区域上进行聚类得到对方球队进攻关键区域,最后依据球队的关键区域和进攻过程中的重点球员建立了合理的防守策略。仿真实验表明了在球队关键区域上进行针对性的防守的有效性,同时也验证了关键区域计算的正确性。
1 球员进攻策略分析
对比赛中的日志文件做了解析,在日志文件中如果连续的kick动作都是由我方球员发出的,把这些kick动作序列称为一条动作链。如果这条动作链的起点在A队半场,终点在B队禁区线以下的区域(球的位置坐标X>36),把这条动作链称为A队的一次进攻动作链。将一条进攻动作链中的球的位置坐标连起来,得到一条进攻动作链图。如图1所示,是10场比赛A队的所有的进攻动作链图。由球队进攻动作链图可以看出,一支球队在进攻时足球的轨迹在整个球场中的分布并不是均匀的。

图1 球队进攻动作链图Fig. 1 Team attack action chain
在所有的动作链中,如果上一次踢球的球员和下一次踢球的球员不同,视为一次传球(Pass);如果上一次踢球和下一次踢球的球员相同,视为一次带球(Dribble)。将所有的传球动作取出,形成了如图2所示的球员传球热力图。

图2 球员传球热力图Fig. 2 Players try hard to pass the ball
由球员传球热力图可知在一支球队进攻过程中,各球员之间的配合是有侧重点的,不同的阵型和球员之间的不同配合程度导致了如图1所示球的轨迹分布不均匀,不同的区域差距很大。
2 球场动态的划分
2.1 传统的球场离散方法
在大多数数据挖掘算法中,需要将连续的数据或者连续的属性转化为离散的数据。在RoboCup仿真2D中,球场区域的划分大多是基于文献[8]将球场划分为25个区域,如图3所示。
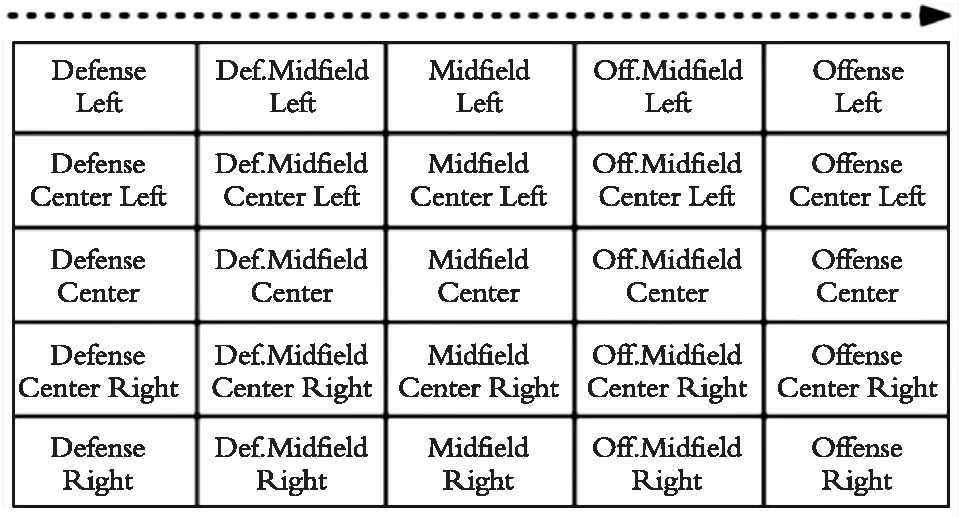
图3 25个区域球场离散图Fig. 3 Discrete map of 25 regional courts
图3中每一个网格可以是一个动作的起点和终点,而这种方法划分的区域过多,在实际使用过程中增加了冗余和计算的复杂。为了较少冗余,类比人类足球,按照人类足球专家的经验将球场离散成如图4所示的5个区域。
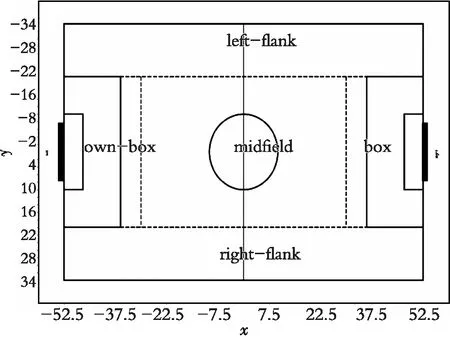
图4 人类足球球场离散图Fig. 4 Discrete diagram of human football field
这种划分方法在计算时带来了很大的便捷,将图3的部分小块区域划分为了一个整体。而这种方法过于拘泥,不够灵活,不能准确反映各球队的特点。由图1可知,球队在进攻时的重点区域是有侧重点的。基于上述情况,对球场的离散方法进行了改进。
2.2 基于数据分布的动态球场离散方法
不同球队由于进攻侧重点不同其在进攻时球的位置分布也是不同的,根据这一事实采用了基于数据分布的离散方法动态的对球场进行了划分。类比RoboCup仿真足球,首先从球队进攻动作链中提取球的位置坐标(x,y),将动作链中所有球的位置提取出来构成一个由二维坐标组成的集合P={(x1,y1),(x2,y2),…,(xn,yn)}。
为了使球场的划分更加科学和准确,对集合P中的点分别统计其在x轴和y轴上的数据分布特征[9]。将集合P中的点在x轴上进行投影操作,使其变成由x轴上的点组成的一维向量X=(x1,x2,…,xn),将集合P中的点在y轴上进行投影操作,使其变成由y轴上的点组成的一维向量Y=(y1,y2,…,yn),在每一维上对数据的频度分布采用标准正态分布曲线进行拟合。
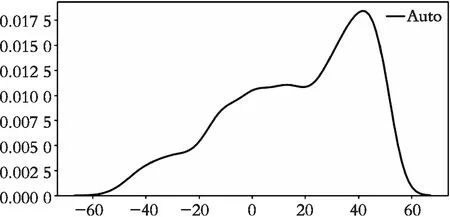
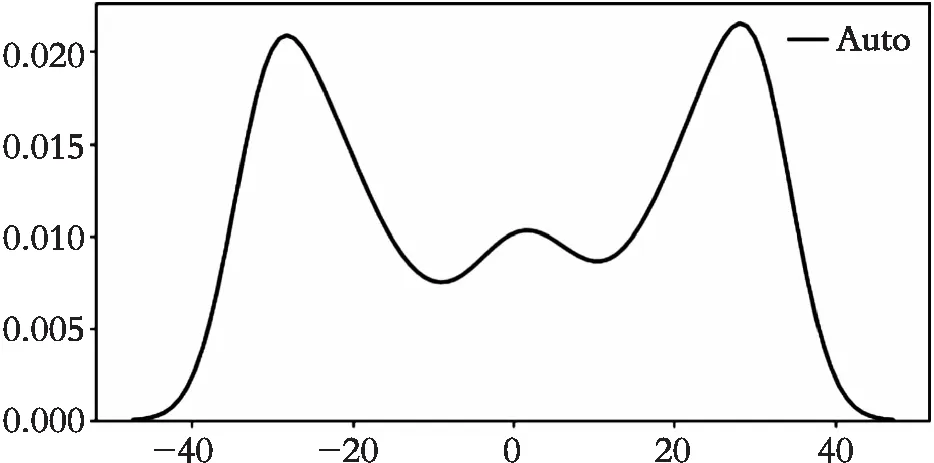
图5所示是A队与B队的10场比赛中A队在进攻其球的位置数据分别投影在x轴和y轴上的数据分布图(图5(a)是x轴上的数据分布,图5(b)是y轴上的数据分布)。可以看到,在不同维度上仿真足球的数据分布于图4非常相似。x轴上的分布呈现3个区域,20以后的部分密度增长迅速,y轴上呈现3个区域且3个区域密度差距较大。由于在进攻时对方半场的区域远远比A队半场重要,所以依据此图对球场划分为图6所示4个部分:
(1) 在X方向以20为界分为 (-60,20)和(20,60)两个部分。
(2) 在Y方向上以-10和10为界分为(-40,-10)、(-10,10)和(10,40)3个部分。
(a) x轴数据分布
(b) y轴数据分布
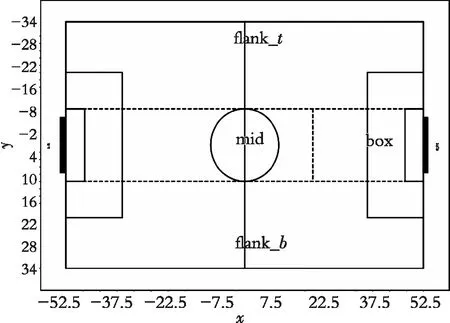
图6 球场分区域图Fig. 6 Court area map
3 基于自适应参数算法的球队进攻关键区域计算
3.1 自适应参数密度聚类的相关概念
3.1.1 相关定义
聚类算法是无监督学习方法的一种,它可以自动的将大量的数据分成属性相同的若干簇。密度聚类(DBSCAN)算法属于聚类算法中的一种,在1996年被首次提出[9],算法的优点是对于噪声数据不敏感且不用人为指定划分簇的数目,但是算法的缺点是需要依据人为经验指定邻域(Eps)和邻域内最少点的个数(MinPts)两个参数,用来作为将数据划分簇的依据,因此DBSCAN算法对Eps和MinPts的参数十分敏感。针对这一问题,文献[10]提出一种自适应确定DBSCAN算法参数的算法(KANN-DBSCAN),利用数据本身分布的特性来自动计算最优的Eps和Minpts两个参数,下面给出KANN-DBSCAN算法的相关定义。给定数据集D={x1,x2,…,xm}:
定义1 Eps邻域:对xj∈D,xj之间的距离小于等于Eps,即NEps(xj)={xi∈D|dist(xi,xj)≤Eps};
定义2 核心对象:如果样本在以Eps为邻域且包含的样本个数大于等于MinPts个的区域中,即|NEps(xj)|≥MinPts,则称xj为一个核心对象;
定义3 密度直达:如果xj在xi的邻域中且xi为一个核心对象,则称xj由xi密度直达;
定义4 密度可达:在xi与xj之间由若干个样本序列,并且若干个样本序列后一个样本由前一个样本密度直达,则称xj由xi密度可达;
定义5 密度相连:对于样本xi与xj,如果xi与xj均是由另一个样本密度可达,则称xi与xj是密度相连的;
定义6 簇:存在两个数据集合C和D且C是D的非空子集,则对于C和D如果:
(1) 对与样本xi,有样本xj∈C且xi是从核心对象xj密度可达的,则对象xj∈C。
(2) 对任意xj,xi∈C,xj和xi是密度相连的,则称数据集合C为簇;
定义7 噪声点:如果样本xi不属于任何簇,则xi为噪声点,即noise={xi∈D|∀k∶∉Ck};
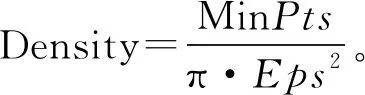
3.1.2 算法思想
DBSCAN算法需要确定用Eps和MinPts两个参数来将足够密度的区域划分为簇,形成满足密度相连的点的最大集合[9],而Eps和MinPts的值往往需要根据先验知识来设定,受主观因素影响较多,取值不当会导致聚类结果错误。KANN-DBSCAN算法利用数据集自身分布的特点计算Eps和MinPts候选项,使用这些候选项进行DBSCAN算法聚类。如果至少3个连续的候选项聚类类别相同,则选择Eps相对较大的作为算法的Eps参数,并得到对应的MinPts参数,聚类结果具有较高的准确性[12]。
3.1.3 算法步骤
步骤1 对数据集D中每两个样本点的距离进行计算,形成距离分布矩阵[11],即
Dn×n={Dist(i,j)|1≤i≤n,1≤j≤n}
(1)
其中,Dn×n为n×n中的元素是D中每两个样本之间的距离;数据集中的样本个数为n;数据集中任意两个样本i和j之间的距离为Dist(i,j)。
步骤2 矩阵Dn×n为数据集D的距离矩阵,对其中的每一行升序排序,排序过后的每一列即为第K列的K-最近邻向量Dk,其中第一列的元素全部为0,因为其为样本到自身的距离。
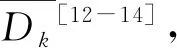
(2)
步骤4 针对步骤3计算得到的Eps候选列表,分别再计算列表中每一个Eps邻域中样本对象的数量,将多有样本对象的Eps邻域中的样本数量的期望作为MinPts参数,即
(3)
其中,Pi是对象i的Eps邻域中样本对象的数量,在数据集D中的对象总数为n。
步骤5 依次选择由步骤3得到的候选参数列表中的不同Eps和步骤4得到的MinPts参数,进行DBSCAN聚类计算,分别记录不同K值得到的簇数,当K对应的簇数连续3次相同时,认为结果已经稳定,选取此时对应的簇数N为最优簇数。
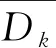
3.2 球队进攻关键区域的计算
选取上述A队与B队的10场比赛,按照图6所示对球场划分为4个区域。每一个区域是由一系列由球的位置所构成的点集合即
Pk={(X1,Y1),(X2,Y2)…(Xmk,Ymk)}
(4)
其中,k为关键区域,k=1表示mid区域,k=2表示box区域,k=3表示flank_t区域,k=4表示flank_b区域。经过计算得到mid区域的点有589个,即m1=589,box区域的点有119个,即m2=119,flank_t区域的点有1 644个,即m3=1 644,flank_b区域的点有1 663个,即m4=1 663。
计算球队进攻关键区域分为几个步骤:
Step 1计算数据集Pk(k=1,2,3,4)的距离分布矩阵:
P1=[[0.,0.,3.86,…,39.37,6.63,7.11]
[0.,0.,3.86,…,39.37,6.63,7.11]
…
[7.11,7.11,9.38,…,46.33,1.17,0]]
P2=[[0.,0.56,13.,…,13.67,13.44,15.33]
[0.560.,12.47,…,13.33,13.15,15.08]
…
[15.33,15.08,11.24,…,3.212.34,0]]
P3=[[0.,1.44,3.36,…,14.05,14.2,14.47]
[1.44,0.,1.92,…,12.74,12.87,13.13]
…
[14.47,13.13,11.4,…,0.8,0.56,0]]
P4=[[0.,0.51,2.57,…,19.7,21.44,24.22]
[0.51,0.,2.19,…,19.28,20.99,23.84]
…
[24.22,23.84,21.66,…,5.41,5.59,0]]
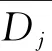
DE1=[0.589,0.904,… 57.093,57.605]
DE2=[0.661,1.097,… 20.152,20.790]
DE3=[0.611,0.914,… 79.036,79.145]
DE4=[0.633,0.967,… 74.339,75.095]
Step 3根据所求出的Eps列表对应的Eps领域个数并且其数量的数学期望得到对应的MinPts参数列表MPk分别为
MP1=[2.477,3.961,… 563.031,563.985]
MP2=[2.597,4.294,… 113.219,114.076]
MP3=[2.245,3.509,… 881.611,881.798]
MP4=[2.191,3.729,… 866.622,868.873]
Step 4分别将DEk和MPk中的对应值代入聚类算法进行计算,得到不同K值对应的簇数。选择连续的簇数3次相同且最大的簇数对应的K值所对应的Eps和MinPts值为最优的值。
伪代码如下:
fori in (EpsCandidate_length)//循环Eps候选集
cluster=DBSCAN(EpsCandidate[i],MinptsCandidate[i])//返回计算Eps对应的MinPts值的簇数列表
cluster.sort()//将簇数列表从大到小排序
foriin range(cluster_length):
k=i//循环所有的簇数
while cluster[i]==cluster[i+1]:
ifi+2 < cluster_length:
i=i+1//当前簇数和下一个簇数相等时,再比较下一个
ifi-k>=2://当连续的簇数相同次数达到3 此时,输出对应的Eps和MinPts
print(EpsCandidate[i])
print(MinptsCandidate[i])
经过上述计算得到每个区域的Eps和Minpts参数,如表1所示。

表1 A队在不同区域的Eps和MinPts值Table 1 Team A’s Eps and MinPts values in different areas
Step5 在mid、box、flank_t、flank_b4个区域中,按照表1所计算出的参数进行密度聚类。聚类结果如图7所示:
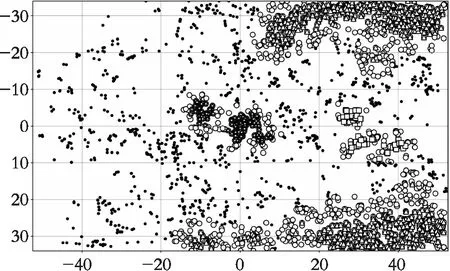
图7 A队聚类结果Fig. 7 Team A clustering results
在图7中圆形的黑点为噪声点,三角形分别为flank_t和flank_b区域的聚类中心,正方形为box区域的聚类中心,星形为mid区域的聚类中心。每一个聚类中心既为一个进攻关键区域,所有的聚类中心既为A队在于B队进行比赛时的进攻关键区域。
4 防守策略优化
4.1 数据的采集
选取Hfut2019国赛队(以下简称Hfut2019队)为基准队,分别于Alice队、MT2019队、YuShan_NB队和YuShan2019队进行10场比赛。在比赛中服务器会实时生成记录比赛的两种文件:一种是记录关于球员执行的命令、球员执行的动作等信息的文件(以下简称RCL文件),一种是记录关于球的位置和速度,球员的位置和速度等信息的文件(以下简称RCG文件)。从RCL文件中取出对方球队的队名和进攻队员信息,根据上下周期球员执行的命令取出对应的RCG文件中足球的位置信息,生成动作链。
4.2 球场的划分
从进攻动作链中提取球的位置坐标,按照上述的球场离散的方法对X和Y方向上的数据的分布做了拟合,不同球队球场上数据的分布如图8所示。
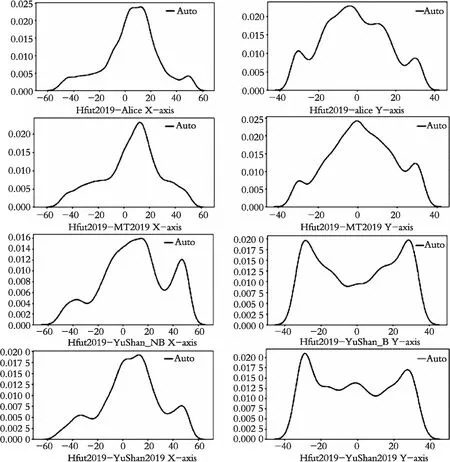
图8 不同球队的数据分布图Fig. 8 The data distribution diagram of the different teams
从图8可以看到,Hfut2019-Alice和Hfut2019-MT2019的数据分布相似,其X轴上数据主要集中在中场,前场数据较少;Y轴上的数据分布也主要集中在中间,两边数据较少。Hfut2019-YuShan_NB和Hfut2019-YuShan2019的数据分布相似,其X轴上的主要集中在中场,而前场区域的数据也有一个顶峰;Y轴上的数据分布主要集中在两边,呈对称分布,中间数据较少。依据不同球队的数据分布图可以将球场分别划分如图9所示区间。
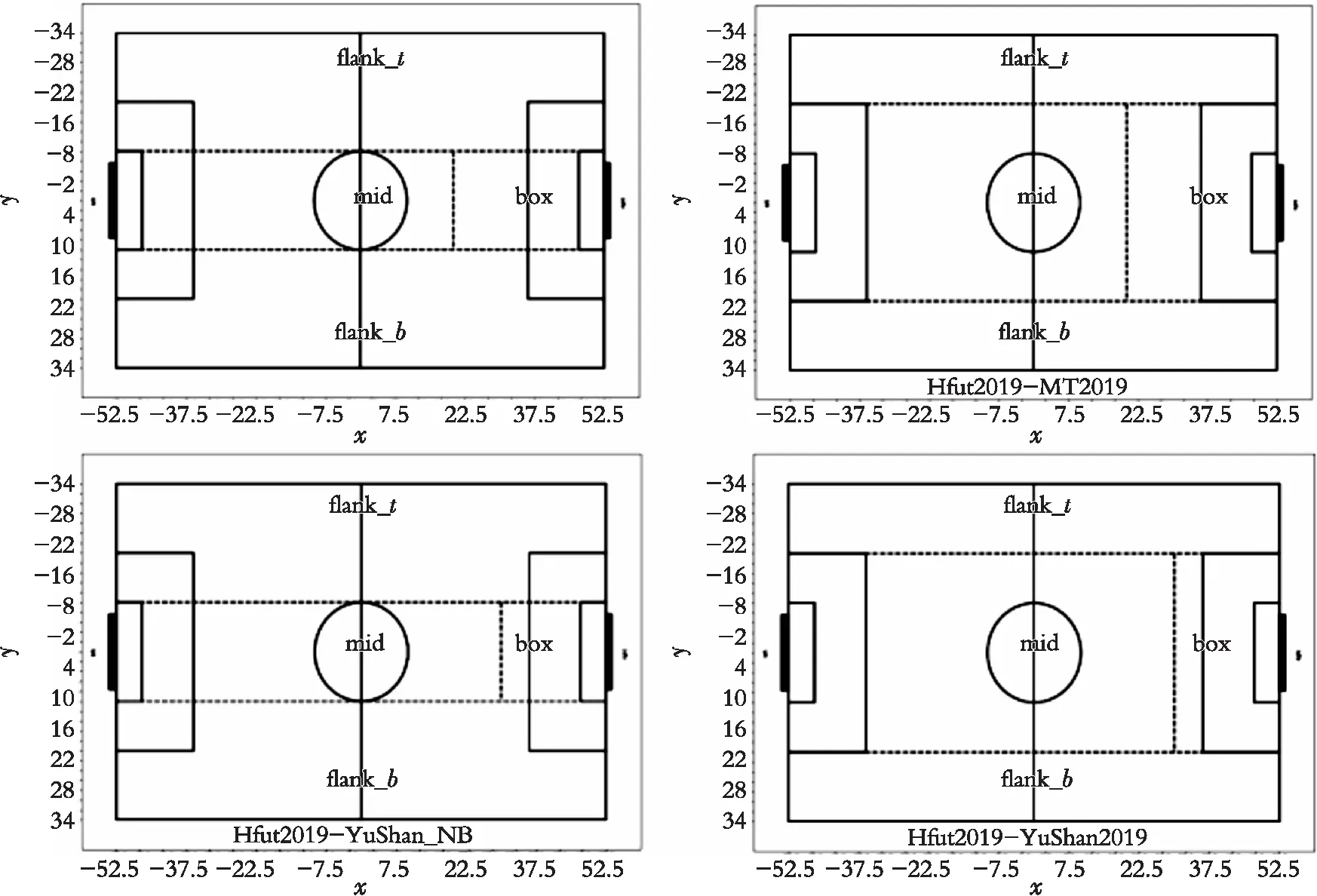
图9 不同球队球场划分Fig. 9 Field division of different teams
(1) Hfut2019-Alice:在Y方向上分为(-40,-20)、(-20,20)和(20,40)3个部分;在X方向上分为(-52.5,30)和(30,52.5)两个部分;
(2) Hfut2019-MT2019:在Y方向上分为(-40,-20)、(-20,20)和(20,40)3个部分;在X方向上分为(-52.5,20)和(20,52.5)两个部分;
(3) Hfut2019-YuShan_NB:在Y方向上分为(-40,-10)、(-10,10)和(10,40)3个部分;在X方向上分为(-52.5,30)和(30,52.5)两个部分;
(4) Hfut2019-YuShan2019:在Y方向上分为(-40,-20)、(-20,20)和(20,40)3个部分;在X方向上分为(-52.5,30)和(30,52.5)两个部分。
4.3 进攻关键区域计算与防守策略分析
使用自适应DBSCAN算法分别计算不同球队在不同区域的Eps和MinPts值,如表2所示:
将不同队伍10场比赛中的球的位置坐标在一个球场进行表示,按照表2所示不同区域的Eps和MinPts值对这些位置坐标进行分区域DBSCAN聚类得到进攻关键区域,并且根据传球热力图取出10场比赛的相互传球超过70次的重点球员结合其进攻阵型得到传球序对,如图10所示,其中Hfut2019-Alice和Hfut2019-MT2019 的打法很类似,选取Hfut2019-Alice作为分析对象。
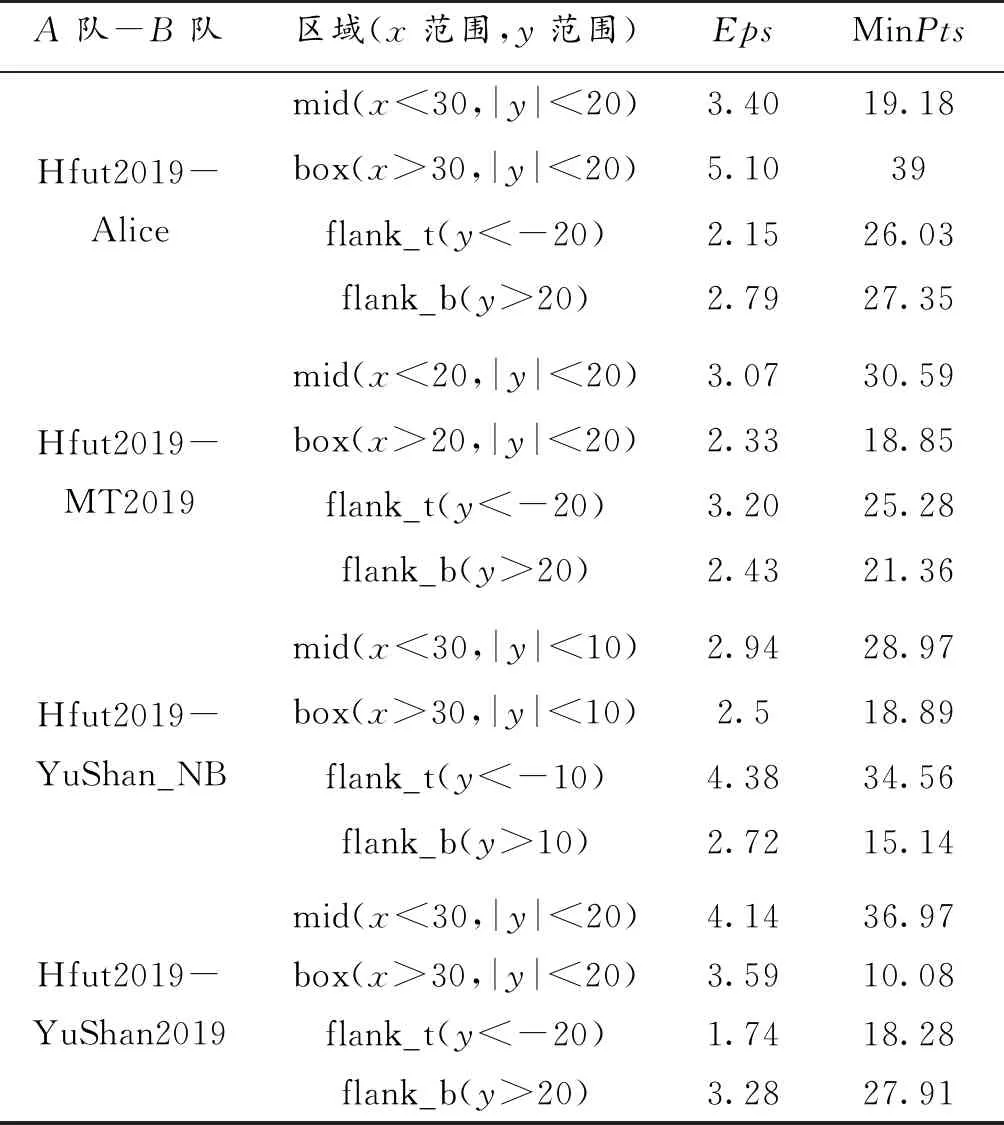
表2 不同球队在不同区域的Eps和MinPts值Table 2 Eps and MinPts values for different teams in different areas
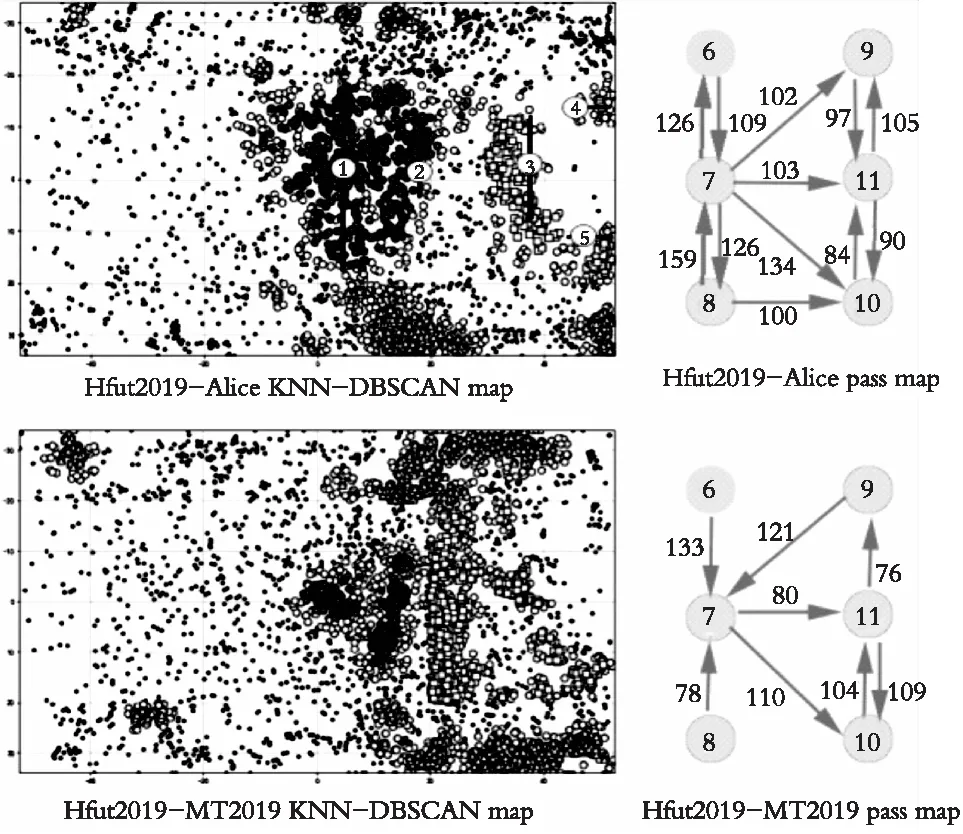
图10 自适应DBSCAN和传球序对图(1)Fig. 10 Adaptive DBSCAN and pass sequence pair diagrams (1)
在自适应DBCSAN图中,不同的颜色代表不同的聚类簇,flank_t和flank_b的聚类结果用三角形表示、mid区域的聚类结果用星形表示、box区域的聚类结果用正方形表示,绿色圆圈内的数字表示进攻关键区域,共有5个关键区域。在传球序对图中绿色圆内的数字表示球员号,箭头表示球从几号球员传向几号球员,箭头旁的数字表示两个球员之间传球的次数。从传球序对图中我们可以得到其进攻时球员之间的配合策略:
(1) 由7号球员将球传给前锋,从中路往下进行运球。
(2) 7号球员为进攻时的核心球员,是连接中场与前场的枢纽。
(3) 在进攻时9号、10号、11号3个前锋配合得十分密切。
根据Hfut2019-Alice的进攻关键区域和传球序对,Alice可以适当调整球员来进行3层防守,如图9中的“Hfut2019-Alice 自适应DBSCAN图”所示:
(1) 将前锋适当撤回至图中“1”区域,在中场进行防守。
(2) 可将中场的部分球员放在“2”区域,看住对方7号球员。
(3) 在禁区附近,将剩余中场球员和部分后卫放在“4”和“5”区域,阻截对方的传球,其他球员放在“3”区域,阻止对方射门。
用同样的方法可以得到Hfut2019-YuShan_NB和Hfut2019-YuShan2019的进攻关键区域和重点球员传球序对图,如图11所示。从图11上看它们的打法类似,选取Hfut2019-YuShan_NB作为分析对象。
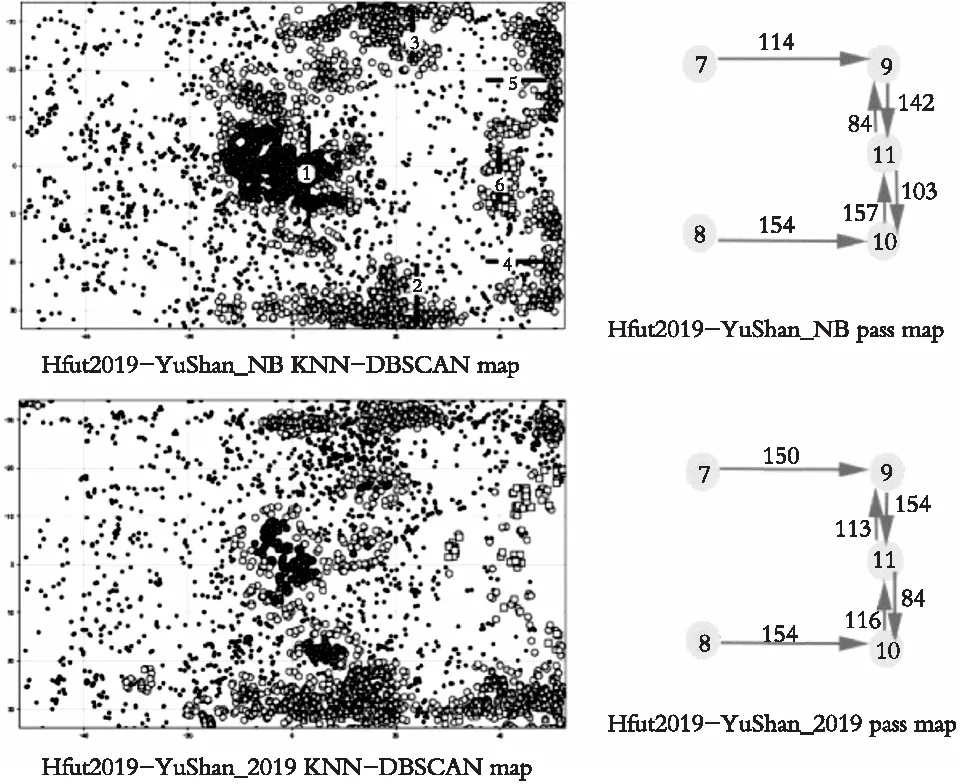
图11 自适应DBSCAN和传球序对图(2)Fig. 11 Adaptive DBSCAN and pass sequence pair diagrams (2)
从传球序对图中可以得到Hfut2019在与YuShan_NB比赛进攻时球员之间的配合策略:
(1) 由边路7号、8号将球传至给前锋9号、10号,沿着边路往下进行运球。
(2) 在进攻时9号、10号、11号之间配合的比较密切。
根据Hfut2019-YuShan_NB的进攻关键区域和传球序对,YuShan_NB可以适当调整球员来进行3层防守,如图9中的“Hfut2019-YuShan_NB 自适应DBSCAN图”所示:
(1) 在6“”区域,将对方11号球员看住,防止其接球射门,阻止对方7号和9号,8号和10号之间的传球。
(2) 可将前锋适当的撤回至“1”区域,参与中场防守。
(3) 中场可将部分球员放置在“2”和“3”区域,阻止其沿边路下球。
(4) 在禁区附近,将剩余中场球员和部分后卫放在“4”和“5”处,阻截对方的传球,其他球员放在“6”处,阻止对方射门。
5 仿真实验
选取Hfut2019-YuShan_NB作为分析对象(Hfut2019简称H队,YuShan_NB简称Y队),修改YuShan_NB的代码,进行了仿真实验。按照上述分析的防守策略制定了3个方案:
(1)Y队的6号球员看住H队的11号。Y队的8号往对方7号和9号之间跑位,使得H队7号传球给9号受到限制。Y队7号往H队8号和10号之间跑位,使得H队8号传球给10号受到限制。
(2) 在边路的“2”和“3”号区域,Y队的4号和5号球员按照最大力量去跑位,阻止H队的9号和10号沿边路下底,并且在“5”和“4”区域使其最大程度去逼抢球。
(3) 在方案B和A的基础上,在禁区内的6号区域,让Y队的2号和3号看住H队球员防止其射门,并且将我方前锋撤回至中场1号区域适当的参与防守。
让Hfut2019队分别于改过之后的球队(按照1、2、3方案改动的球队以下分别称为A队、B队和C队)分别进行10场比赛,记录下每十场比赛的总进球数、总丢球数和平球场次如表3所示。
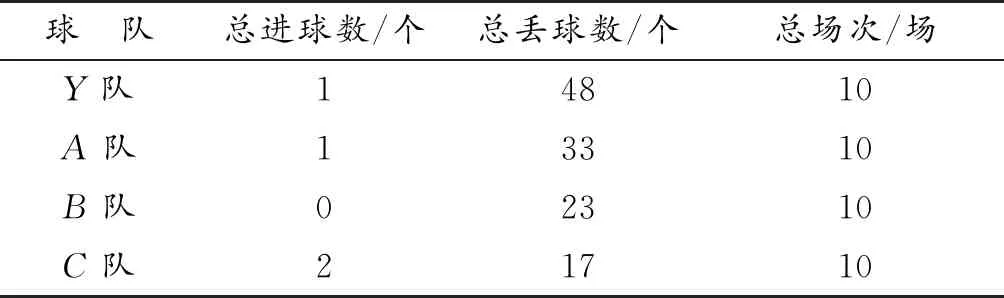
表3 改进的球队与Hfut2019测试数据Table 3 Improved team with Hfut2019 test data
从表3中可以看到,改进之后的A、B、C队的10场比赛总丢球数相比Y队有了很大程度的减少,而对球队的进球进攻性没有显著的影响。进一步提取10场比赛的平均丢球率在柱状图上和YuShan_NB进行对比,如图12所示。
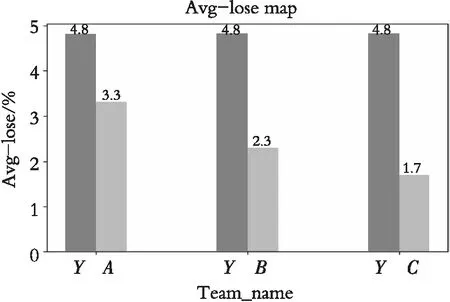
图12 球队平均丢球率Fig. 12 The team’s average percentage of ball-losing
从图12可以看到,A、B和C3个方案对球队防守的改进都有明显的效果,球队的丢球率明显减少,其中C版本丢球率减少到1.7%,效果最显著。仿真实验说明了防守策略和A、B、C3个方案的有效性,同时也验证了球队进攻关键区域提取的正确性。
6 结 语
通对数据挖掘的方法依据比赛时球的数据分布对球场进行了动态的离散,在每一个动态划分的区域内使用自适应参数DBSCAN算法提取了球队的进攻关键区域,并且根据球队进攻关键区域和进攻过程中的重点球员建立了合理的防守策略。最后的实验通过在底层球队的代码上加入防守策略使得底层球队的丢球率从每场4.8个球下降到了每场1.7个球,验证了球队进攻区域提取的正确性,也说明了方法确实可以应用在RoboCup仿真2D比赛中,给球队的代码优化指明了方向。如果能进一步依据对手的防守状态修改我方的进攻策略,使得球队进攻和防守策略相结合,那么球队代码的优化会更加合理。

