扰动下混合时滞耦合动态网络的脉冲同步*

杜师师， 李 兵**， 邹 聪

(重庆交通大学 数学与统计学院，重庆 400074)

0 引 言

耦合动态网络的应用十分广泛，其同步性分析是应用的前提[1-5]。由于网络节点信息传输速度的限制，时滞普遍存在并可能引起网络的不稳定现象[6-8]。另外，信号传输中的频率改变可能产生脉冲信号,不同的脉冲信号对耦合动态网络的影响也各不相同。近年来，学者们针对时滞耦合动态网络的脉冲同步性问题，展开了广泛的研究并已取得大量很有意义的成果[9-18]。除了时滞和脉冲以外，随机噪声和外部扰动也时刻影响着网络节点的动态行为，最近已有学者在随机耦合网络的同步性研究方面，陆续得到一些有价值的理论成果[19-27]。

值得注意的是，文献[1-27]都是分别讨论脉冲信号和随机噪声对耦合动态网络同步过程的影响。然而在实际问题中，脉冲信号和随机扰动常常同时出现，共同影响耦合网络的动态行为与同步控制。其次，已有研究往往只考虑了单一的有限时滞网络模型，忽略了网络节点并行过程中可能存在的分布时滞的影响。另外，在有界但并不消失的外部扰动影响下，网络节点之间的误差并不会趋于零，因而无法达到已有文献中提出的完全同步性。

基于上述分析，本文将研究具有混合时滞的耦合动态网络在随机噪声和外部扰动影响下的脉冲同步控制问题，主要创新点包括：所考虑的网络模型同时具有混合时滞、随机噪声、外部扰动以及脉冲信号，比已研究的模型更一般，更符合现实需要；引入指数最终有界性指标来刻画同步误差的变化，克服了外部扰动的影响，比文献[7，12，15，18，26，27，28]中的同步性指标更适用；提出了基于改进型混合时滞差分不等式的分析方法和线性矩阵不等式的判据，克服了混合时滞因素的影响，理论结果易于检验。

1 模型描述及预备知识

考虑孤立节点满足下列时滞差分方程：

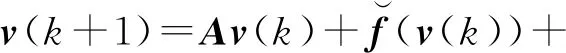
(1)

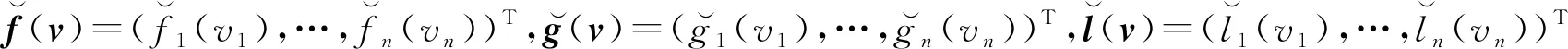
在外部扰动和随机噪声影响下，考虑N个形如式(1)的孤立节点耦合而成的动态网络如下：

(2)

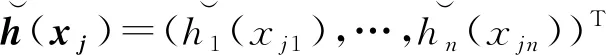
令ei(k)=xi(k)-v(k)，由式(1)(2)可得同步误差系统：

(3)

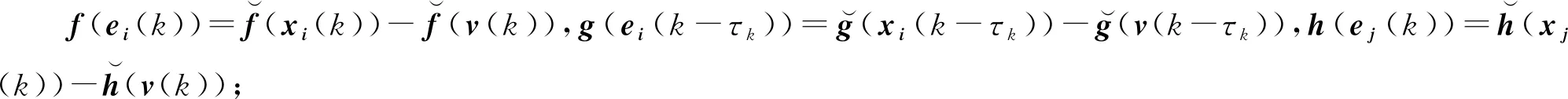
在本文中，给出以下假设：

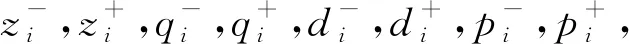
由文献[10]可知，存在4个正对角矩阵H=diag{σ1，…，σn}，=diag{η1，…，ηn}，G=diag{ζ1，…，ζn}和Ψ=diag{ρ1，…，ρn}，使得条件(A1)可等价转化为

(4)

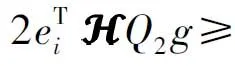
(5)

(6)

(7)

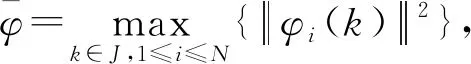
为了得到同步性判据，先给出如下改进的时滞差分不等式：

引理1 假设正实数序列V(k)对任意正整数k≥k0，都满足：

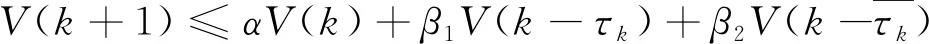
(8)

其中:α，β1，β2，β3，r为已知正常数且满足α+β1+β2+β3<1，那么当V(k)≤v0e-λk+d，k∈(-∞，ko]时，必有V(k)≤v0e-λk+d，k≥ko。

(9)

证明过程与文献[10]类似，故省略。

2 主要结果

定理1 假设(A1)和(A2)成立，且存在正数α，β1，β2，β3，λ满足式(9)，如果存在5个常数β4，，ε，，p以及5个正定对角矩阵，G，Ψ，P，使得

PΓ≤I，APΓ≤εI，Ξ<0

则耦合网络式(3)达到指数最终有界同步，其中

Ξ2=-β1P-HF1，Ξ3=P+η3I-H

Ξ4=P+η3I-，Ξ5=η1I+2εI+2I-G

Ξ6=-β2P-GD1，Ξ7=P+η3I-Ψ

Ξ8=-β3P-ΨΘ1，Ξ9=P+η2I-β4P

η1=λmax(CTC⊗ΓTPΓ)，η2=ελmax(CCT)

η3=

成立。

证明令

则对任意k≠nl，可得

由网络模型式(3)并结合邻接矩阵的性质，可以得到V(k+1)中下列各项分别满足:

(ei(k))f(ei(k))+

将上述不等式及式(4)—式(7)代入V(k+1)并取数学期望，可得

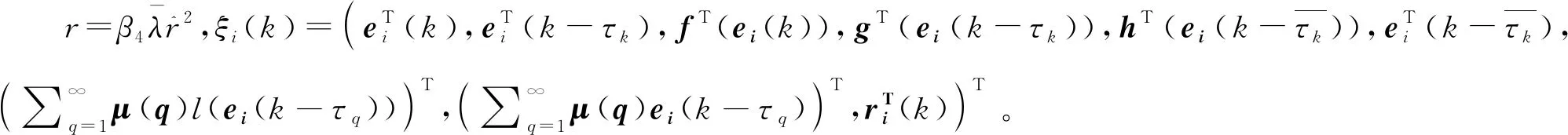
由Ξ<0可知对k≠nl，有式(8)成立，故对k∈[0，n1],有

E{V(k)}≤v0e-λk+d

由式(3)中的第二个方程可得

ei(nl+1)=(I+Binl)ei(nl)

因此有

E{V(nl+1)}≤ρn1eλv0e-λ(n1+1)+ρn1d

假设对l=1，2，…，m，下列不等式成立：

其中：k∈(-∞，nm]，n0=0，Zn0=1。由数学归纳法，可知对任意l∈Z+及k∈[nl-1+1，nl]，有

定理1得证。

3 数值例子

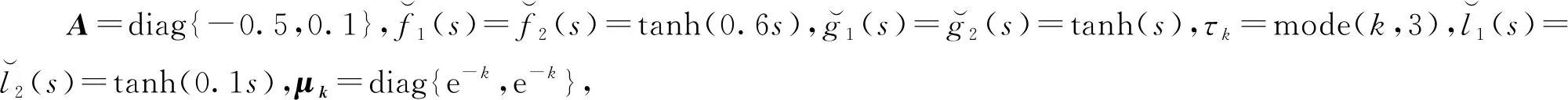
扰动信号为

r1(k)=-2cos(k)，r2(k)=-2sin(k)

σ(k，xi(k)-s(k))=0.05(xi(k)-s(k))

取α=0.3，β1=0.11，β2=0.18，β3=0.16，λ=0.05，Z1=diag{2，3}，Q1=diag{2，3}，D1=diag{3，4}，Θ1=diag{3，4}和Z2=diag{0.003 4，0.003 4}，Q2=diag{0.002 5，0.002 5}，D2=diag{0.001 5，0.001 5}，Θ2=diag{0.002 2，0.002 2}以及θ=0.002 5。

设计脉冲反馈矩阵：

脉冲时刻nl=4l(l∈Z+)，易验证定理1的条件满足，故网络可实现指数最终有界同步，仿真结果如图1、图2所示。

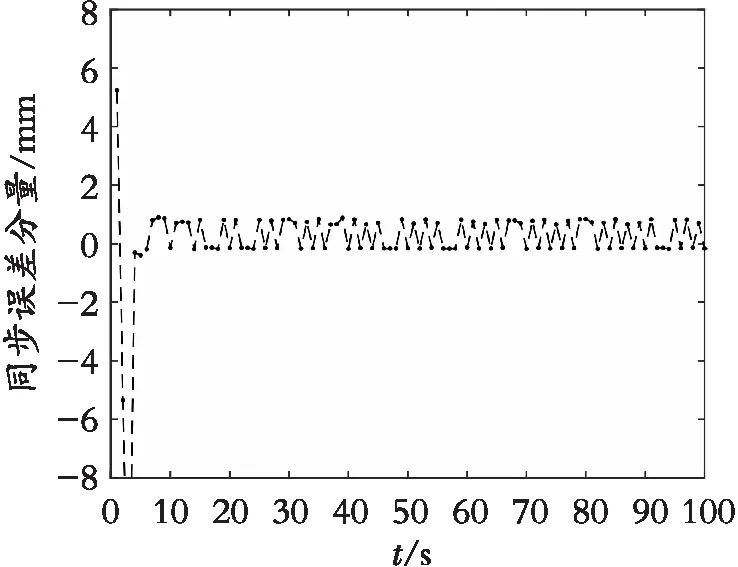
图1 同步误差分量一数值仿真结果Fig. 1 Numerical simulation result of synchronization error fraction 1

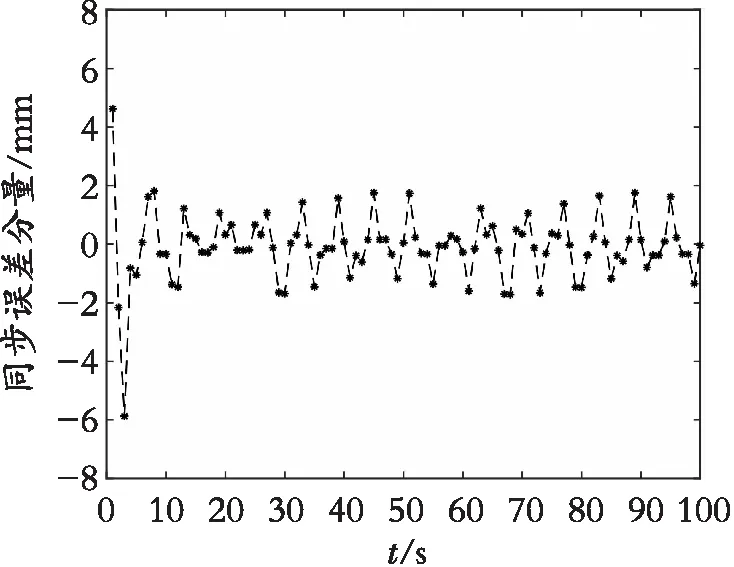
图2 同步误差分量二数值仿真结果Fig. 2 Numerical simulation result of synchronization error fraction 2

4 结果与讨论

本文考虑的耦合动态网络模型中混合时滞和扰动共存，模型更具一般性，所获得的理论成果更具适用性。在外源性有界扰动之下，通过设计脉冲型反馈控制器，使得耦合网络节点状态快速收敛到孤立节点的有界范围内，从而准确刻画出外部扰动对同步误差的影响，解决了传统的完全同步无法实现的问题。通过建立新的混合时滞差分不等式，克服了耦合时滞与分布时滞对误差系统动力学分析造成的困难，改进了已有文献的相关结果。后续将进一步考虑将本文的研究方法推广到马尔科夫跳变网络的脉冲同步控制中。