一类具ψ-Caputo导数的分数阶微分方程 边值问题解的存在性*
董伟萍, 周宗福
(安徽大学 数学科学学院,合肥 230601)
0 引 言
分数阶微积分的概念我们并不陌生,它是整数阶到任意阶的推广。随着自然科学的发展,复杂的工程被大量需求,分数阶微积分理论和它的应用受到极大的关注[1-6]。
近年来,分数阶微分方程在很多科学领域里面都体现得很重要,关于分数阶微分方程边值问题也获得了很好的研究前景。至今,涉及分数阶微分方程边值问题解的唯一性以及多个解存在的情况已经取得了丰富的成果[7-9]。
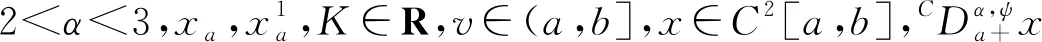
在文献[10]的启发下,本篇文章研究了下面分数阶微分方程的边值问题:
(1)
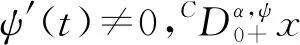
本文在文献[10]的前提下,考虑了高阶的Caputo导数,并且在积分和多点混合边值条件下研究了解的存在性和唯一性,对文献[10]进行了推广。
1 准备知识
在本节中,将介绍贯穿全文的定义、定理和引理。设α>0,I=[a,b]是有限或无限区间,x:[a,b]→R是一个可积函数,ψ:[a,b]→R是一个单调递增的可微函数,并且满足对于任意的t∈[a,b],有ψ′(t)≠0。
定义1[2]ψ-Riemann-Liouville分数阶积分定义如下:
定义2[2]ψ-Caputo分数阶导数定义如下:
其中:
引理1[13]若x∈Cn[a,b],则
其中:n=[α]+1。
引理2[13]如果β∈R,且β>n,则有
其中:n=[α]+1。
引理3[13]如果α,β>0,则有
引理4[13]设x:[a,b]→R是一个函数。
(i) 若x是连续的,则
(ii) 若x∈Cn-1[a,b],则
引理5 分数阶微分方程边值问题式(1)的解等价于下面积分方程:
其中:
证明由引理4知
c1(ψ(t)-ψ(0))+…+cn-1(ψ(t)-ψ(0))n-1
根据x(0)=x′(0)=…=x(n-2)(0)=0,有
c0=c1=…=cn-2=0
则有
(2)
再根据引理2和引理3知
接着由边值条件:
可知
即有
因此,由式(2)知
证毕。
为了方便计算,定义如下式(3):
(3)
2 主要结论
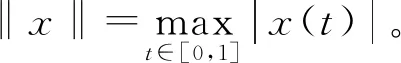
则可以看出算子T的不动点等价问题式(1)有解。
定理1 如果存在常数L1>0,使得
|f(t,x1)-f(t,x2)|≤L1|x1-x2|
∀t∈[0,1],∀x1,x2∈R
且L1B<1,其中B由式(3)给出,则式(1)存在唯一解。
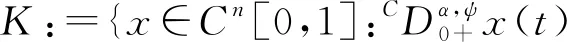
设∀x1,x2∈K,则
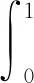
由于0≤L1B<1,故算子T是压缩算子。由Banach压缩映像原理知算子T存在唯一的不动点,即边值问题式(1)存在唯一解。
定理2 如果
(ⅰ) 存在常数L2>0,使得|f(t,x)|≤L2,∀t∈[0,1],∀x∈R。
(ⅱ) 存在实数r>0,使得
则式(1)至少存在一个解。
证明(ⅰ) 令Br:={x∈E:‖x‖≤r},则Br为E中的一个有界凸闭集,由f连续易知T在Br上连续。下面证明T(Br)⊆Br:∀x∈Br,有
故T(Br)⊆Br。
(ⅱ) 下面证明T(Br)是等度连续的。对于∀x∈Br,∀t1,t2∈[0,1]且t1 在本节中,通过具体例子来说明主要结果。 例1 考虑如下分数阶微分方程: (4) 其中: 并且取 通过计算可知 令L1=0.1,则∀t∈[0,1],∀x1,x2∈R,有 且L1B=0.916<1,因此定理1的条件满足。所以由定理1知,边值问题式(4)存在唯一解。 分数阶微分方程作为经典微积分方程的延拓,它的理论分析和数值计算有着很强的实践性,进而衍生出来的解决分数阶微分方程解的方法也变得各式各样。本篇文章中,研究的一类ψ-Caputo分数阶导数,当选取好特殊的函数ψ和对应的微分算子,就可以得到Caputo分数阶导数、Riemann-Liouville分数阶导数、Hadamard分数阶导数等比较常见的分数阶导数。和以前的结果相比较,本文建立的具ψ-Caputo分数阶导数的微分方程的边值条件更为复杂,并且得到的相应问题解的唯一性与存在性充分性条件很合理,通过最后实例也可看出此条件容易满足,具有一定的适用性。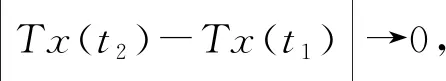
3 实例分析与应用
4 结束语

