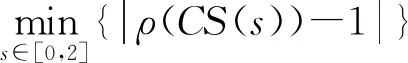递归(分片)仿射分形插值数值模拟与盒维数研究*

袁利国， 余荣忠， 旷菊红

(1.华南农业大学 数学与信息学院,广州 510640；2.九江学院 理学院,江西 九江 332005； 3.五邑大学 数学与计算科学学院,广东 江门 529020)

0 引 言

传统的欧氏几何主要分析规则的几何体，如直线、双曲线、圆、立方体等。而对不规则的对象，如海岸线的长度、自然界的各种形状，传统的几何很难进行处理，而分形几何的创立，对大自然的研究提供了新的思路与方法，分形几何是描述大自然的几何，其分形维数可以更好地衡量不规则体。分形几何引起广泛的研究及应用[1-10]。迭代函数系统(IFS)在分形几何中扮演重要的作用，IFS可以生成各种分形图，如:Koch曲线、Sierpinski三角形、Cantor集、各种植物等。IFS也可应用到插值与拟合极不规则的数据，相比传统的Newton插值与Lagrange插值，有很强的优势。基于IFS的分形插值函数与初等函数一样有自身的几何特征，能用一组IFS表示出来，迭代这组IFS，得到其吸引子，它就是分形插值函数，通常它具有分数维数，是非整数的。在插值已知数据集时，由于吸引子函数(即分形插值函数)有分数维，因此可以插值或拟合不规则的震荡的数据集，比传统的插值方法有优势。常规的分形插值是把整个区间上的数据I=[a,b]，在IFS的某个压缩仿射变换Wk作用下，分别映射到其每个子区间Ik=[xk-1,xk]⊂I上，从而构造一组仿射变换Wk，再基于确定的迭代算法或随机的迭代算法，得到此组IFS的吸引子曲线，此曲线会穿过已知的插值数据点，其迭代函数系中仿射变换的系数公式为

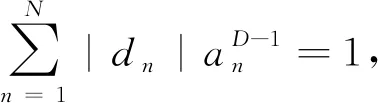
1 递归仿射分形插值

给定区间I=[0,1](或其他的一般区间I=[a,b]也可以)，令0=x0xi-xi-1。设K=[0,1]×R,wi:K→K是仿射映射:

其中,|di|<1,wi把(xl,yl)与(xm,ym)分别映射到(xi-1,yi-1)与(xi,yi)，或把(xl,yl)与(xm,ym)分别映射到(xi,yi)与(xi-1,yi-1)。定义关联矩阵C=(Cij)，如果Jj⊂Ji′，则Cij=1，否则Cij=0。设I(i)={j:Cij=1}，定义映射W=(wij)=(Cijwi)。

(1)

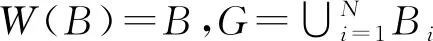
递归分形插值要求满足xm-xl>xi-xi-1，此时有以下3种情形：(1)Ji⊂Ji′ ；(2)Ji⊄Ji′且Ji∩Ji′=Φ；(3)Ji⊄Ji′，但是Ji∩Ji′≠Φ。如果属于第(1)种情形，则递归分形插值也是通常的分片(或称分段、分块)分形插值。如果是第(2)或第(3)种情形，即在文献[1]末尾给出的算例情形，将逐一给出数值分析。

2 递归仿射分形插值数值模拟

递归仿射分形插值本质上也是分块方法[3-4]。文献[5]给出一类多参数递归分形插值函数的数学模型,并进行数值模拟，但给出的代码是仿射分形插值的情形。文献[1]末尾给出的算例的递归结构如图1。此处采用区间I=[0,1.2]，采取等距分割，令

x0=0,x1=0.2,x2=0.4,x3=0.6,x4=0.8,x5=1.0,x6=1.2。设对应y值y0=0,y1=0.8,y2=0.8,y3=0.6,y4=1.0,y5=1.6,y6=0.8。Ji=[xi-1,xi](i=1,2,…,6)，3个Ji′分别为[x0,x2]，[x2,x4]，[x4,x6]。对应的6个仿射变换:w1(x0,y0)=(x0,y0),w1(x2,y2)=(x1,y1),与w1类似[1],由图1可得其他的仿射变换wi(i=2,3，…，6)。

基于图 1的关系，可以分别求得6个仿射变换wi(i=1,2,…,6)的系数，其中di是垂直比例因子(可自由选取)。此处选取d1=0.5,d2=0.6,d3=0.7,d4=0.8,d5=0.6,d6=0.5。对应6组仿射变换的系数为a1=0.5,e1=0,c1=2×(1-d1),f1=0a2=0.5,e2=0.4,c2=-0.5-2d2,f2=0.8a3=0.5,e3=0.6,c3=1.5-0.5d3，f3=0.4-0.6d3；a4=0.5,e4=0,c4=-0.5d4，f4=0.8-0.6d4a5=0.5,e5=0.6,c5=-2+0.5d5，f5=3.2-1.4d5；a6=0.5,e6=0.2,c6=1+0.5d6，f6=-0.2-1.4d6，其中，L-1=1/0.4。

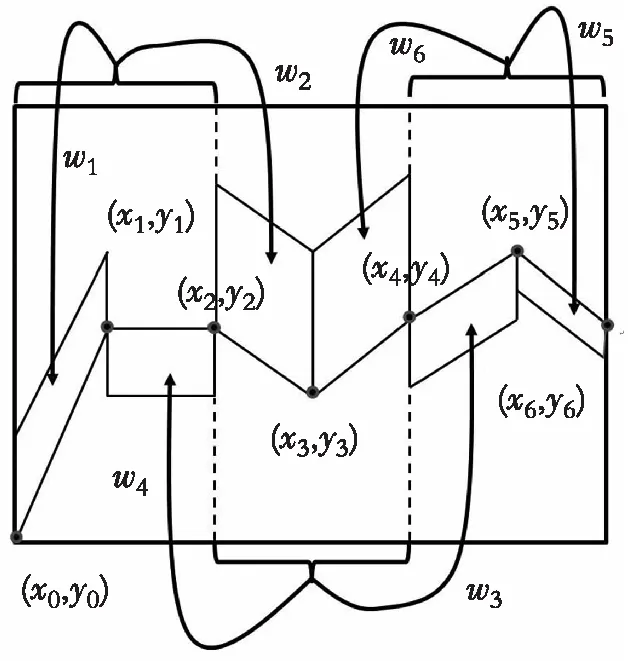
图1 递归仿射变换结构Fig. 1 Structure of recurrent affine transformation

此递归结构的关联矩阵为

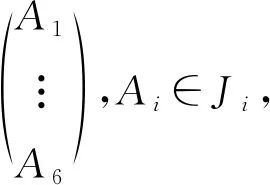
下面提出一类随机迭代算法，更简单且能达到递归分形插值目的。

(1) 初始化，设定自由参数dn(n=1,2,…,6)、最大迭代次数与插值数据点(x0,y0),(x1,y1),…,(x6,y6)等。

(2) 依据数据计算出迭代函数的系数an,en,cn,fn，得到wn(n=1,2,…,6)。

(3) 给定初始值(取(x1,y1)=(0,0))，判定x1落在哪个区间Ji上。因此，每个Ji上对应有两个仿射变换，产生一个随机数，决定由其中的哪一个wi作用到(x1,y1)，生成新的点(x(k),y(k))，同时，把(x(k),y(k))赋值给(x1,y1)，再重复上面的过程。

(4) 直至达到最大迭代次数，则输出所得数据，即递归分形插值曲线。详细程序代码见http://ylgdiy.bokee.com/507551074.html。所得插值结果如图2所示。文献[1]中的递归分形插值构造，其中的所有变换wi,i=1,2,…,6满足要求xm-xl>xi-xi-1，且是情形(1)Ji⊂Ji′与情形(2)Ji⊄Ji′且Ji∩Ji′=Φ的混合形式。

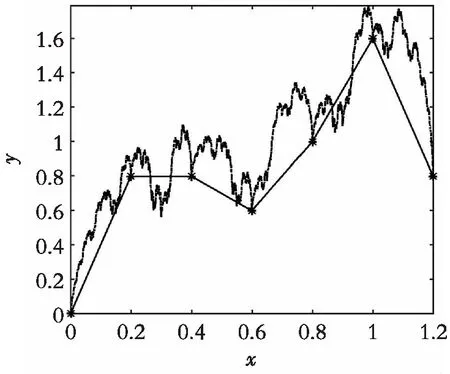
图2 递归仿射分形插值曲线Fig. 2 Recurrent affine fractal interpolation curve

3 分片仿射分形插值

分片(或称分块、分段)形插值是递归分形插值的特殊情形[2,8-9]，有联系也有一定的区别。下面分两种情况讨论，一是分片区间之间是没有重叠情形。另一种是分片区间有重叠情形，现构造如下有重叠情形的分片分形插值，如图3所示。它符合递归分形插值的要求:xm-xl>xi-xi-1，且有Jj⊂Ji′，是第(1)种情形。Ji′,i=1,2,3，三区间无重叠区域。对应的6个仿射变换都采用把(xl,yl)与(xm,ym)分别映射到(xi-1,yi-1)与(xi,yi)。此递归结构的关联矩阵为

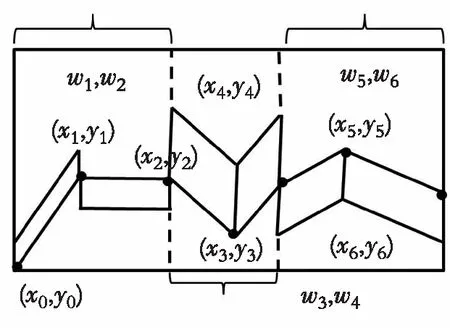
图3 分片仿射分形插值结构(无重叠)Fig. 3 Structure of piecewise affine fractal interpolation (no overlap)

分别求得6个仿射变换wi(i=1,2,…,6)的系数，其中di(i=1,2,…,6)是垂直比例因子，自由选取。d1=0.6,d2=0.8,d3=0.65,d4=0.7,d5=0.66,d6=0.6,6组系数分别为a1=0.5,e1=0,c1=2×(1-d1),f1=0;a2=0.5,e2=0.2,c2=-2d2,f2=0.8;a3=0.5,e3=0.2,c3=-0.5-0.5d3,f3=1-0.6d3;a4=0.5,e4=0.4,c4=1-0.5d4,f4=0.2-0.6d4;a5=0.5,e5=0.4,c5=1.5+0.5d5,f5=-0.2-1.4d5;a6=0.5,e6=0.6,c6=-2+0.5d6,f6=3.2-1.4d6。图4为分片仿射分形插值曲线(无重叠)。采用随机迭代算法，Matlab程序见http://ylgdiy.bokee.com/507560391.html。

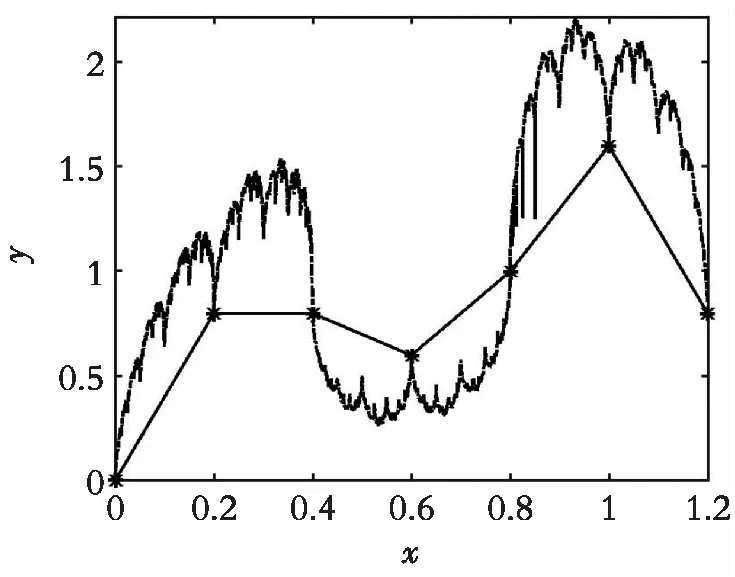
图4 分片仿射分形插值曲线(无重叠)Fig. 4 Piecewise affine fractal interpolation curve (no overlap)

针对分片区间有重叠情形，J1′与J2′有部分重叠区域。现构造如下递归(分片)分形插值重叠情形(图5)，它符合递归分形插值的要求:xm-xl>xi-xi-1，且此时有Jj⊂Ji′，是第(1)种情形。

图5 分片仿射分形插值结构(重叠)Fig. 5 Structure of piecewise affine fractal interpolation (overlap)

对应的8个仿射变换:w1(x0,y0)=(x0,y0),w1(x4,y4)=(x1,y1),其他的类似。因此，可以分别求得仿射变换wi(i=1,2,…,8)的系数，其中di(i=1,2,…,8)是垂直比例因子，自由选取。具体取d1=0.6,d2=0.5,d3=0.4,d4=0.3,d5=0.3,d6=0.6,d7=0.5,d8=0.4,8组系数:a1=0.25,e1=0,c1=1-1.25d1,f1=0；a2=0.25,e2=0.2,c2=-1.25d2,f2=0.8；a3=0.25,e3=0.4,c3=-0.25-1.25d3,f3=0.8;a4=0.25,e4=0.6,c4=0.5-1.25d4,f4=0.6;a5=0.25,e5=0.3,c5=-0.25,f5=0.9-0.8d5;a6=0.25,e6=0.5,c6=0.5,f6=0.4-0.8d6;a7=0.25,e7=0.7,c7=0.75,f7=0.7-0.8d7;a8=0.25,e8=0.9,c8=-1.0,f8=2-0.8d8。相应的分形插值曲线如图6 所示，其中重叠区域的插值曲线更复杂。相应的程序代码可参考http://ylgdiy.bokee.com/507560394.html。

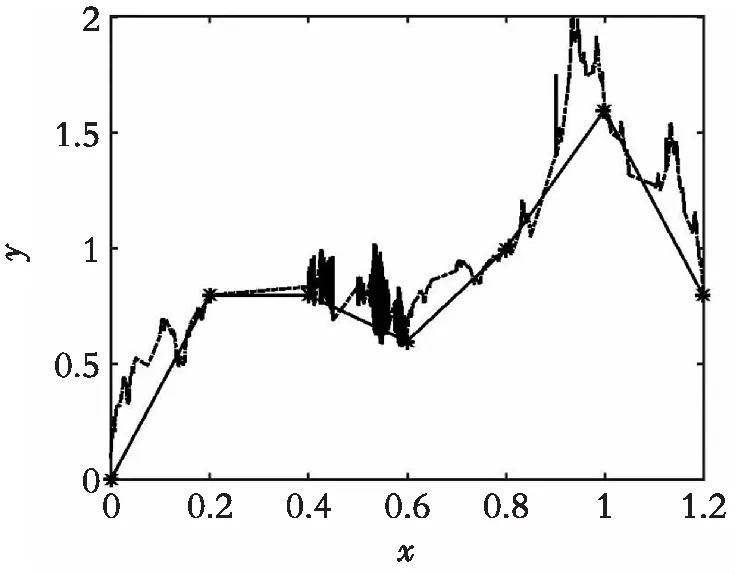
图6 分片仿射分形插值曲线(重叠)Fig. 6 Piecewise affine fractal interpolation curve (overlap)

此递归结构的关联矩阵为

4 仿射分形插值的盒维数

仿射分形插值曲线的盒维数有如下结论:

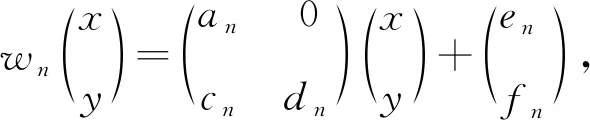
(2)

的解，否则分形维数是1[3-4,7]。

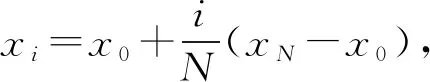
但现实中的插值数据通常不是等距的。此时求解式(2)的精确解是很难。现在提出把分形维数的求解转化为最优化问题式(3)，即

(3)

再采用粒子群最优化算法处理问题式(3),现给出两个算例。

最大迭代次数为80。重复运行10次程序，取10次结果的平均值，即得到最优分形维数值为D=1.758 146 555 910 46。二者之间的误差达到了10-13，其中某一次的收敛过程如图7所示，很快可以收敛到真实值，大概在第10步左右。

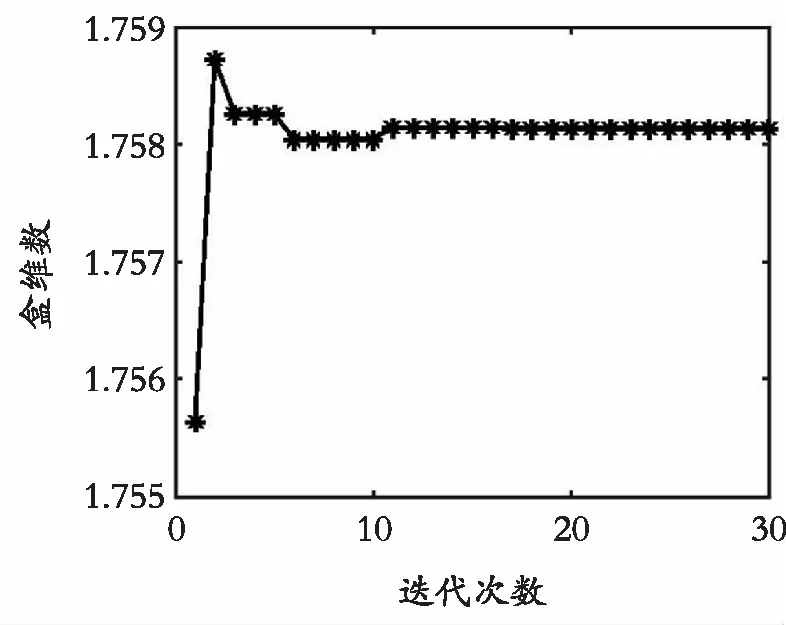
图7 分形维数收敛过程Fig. 7 Convergence process of fractal dimension

算例2 设插值点{(0,0),(30,50),(60,40),(100,10)}，选取d1=0.5,d2=-0.5,d3=0.23,则a1=0.3,a2=0.3,a3=0.4。精确的分形维数D=1.180 2[10]。构造目标函数：

最大迭代数为80。重复运行10次程序，取10次结果的平均值，即得到最优分形维数值为D=1.180 163 827 574 234。二者之间的误差达到了10-5，其中某一次的收敛过程如图8所示。Matlab程序详情见网页http://ylgdiy.bokee.com/507560407.html。算例1的程序比这个简单，只需修改相应的目标函数即可。

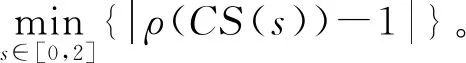
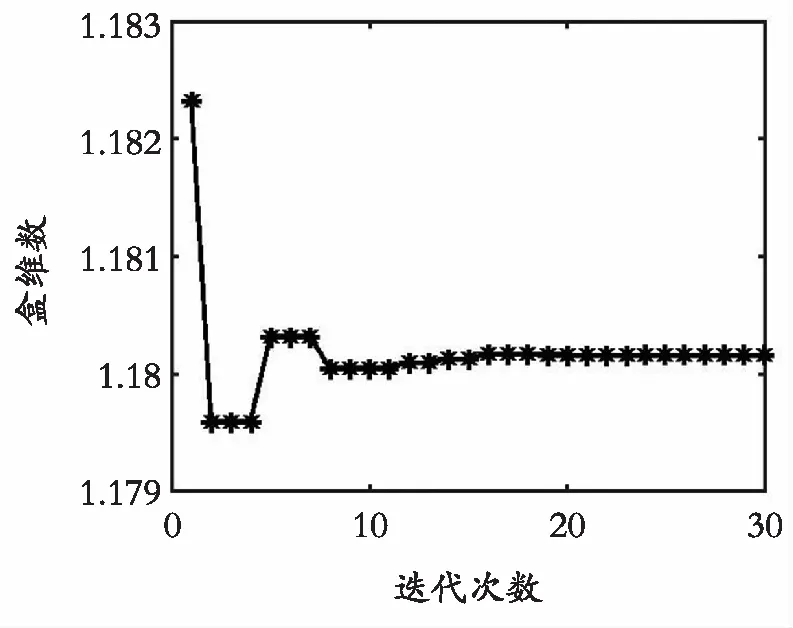
图8 分形维数收敛过程Fig. 8 Convergence process of fractal dimension

5 结束语

对于数据量较大的插值拟合，如经济数据、农业数据、自然现象的长时间数据等，常采用分片的思想来处理，应用也较广，其本质上也是递归分形插值思想。递归仿射分形插值应用到实际数据量较大的情形比较少见。对递归分形插值与分片分形插值的数值模拟给出了分析与算法程序，这为支撑相关理论分析及应用到实际问题提供了补充。程序可稍微修改，更具有一般的适用性与通用性。随后也对仿射变换的盒维数求解给出最优化求解思路，此方法可取得很好的结果。