碳减排下的汽车零部件循环取货路径优化研究*

何茵楠， 王帮俊， 魏宇茜， 吴传良

(1.淮南师范学院 经济与管理学院，安徽 淮南 232001； 2.中国矿业大学 管理学院，江苏 徐州 221116)

0 引 言

随着全球变暖，以CO2为主的温室气体的排放控制与测算，已成为各个领域关注的焦点问题之一。对于汽车制造业而言，能源消耗高、碳排放量大的问题渐渐显露，如何在碳减排的约束下提高生产效率，降低物流总成本是汽车制造企业需要研究的重要问题。 汽车物流中的零部件进厂物流是企业提高生产效率的关键，更是成为推动汽车产业发展的重要环节。目前，零部件进厂物流分为供应商直接送货模式、TPL循环取货模式以及配送中心中转供货模式，大多数汽车制造商采用的是比较先进的循环取货模式。

循环取货中的车辆路径问题是典型的物流配送组合优化问题，是车辆配送活动的重要组成部分，科学地安排运输车辆的行驶路线不仅可以节约运输成本，提升企业物流服务质量，而且能够降低CO2排放量，对环境保护有着重要的意义。刘云等[1]在VRP模型的基础上加入了车辆等待的最大容忍时间和最大运输时间的约束，建立了以总行驶路径最短和车辆使用数量最小的双目标数学模型；Belhaiza[2]提出了带有多时间窗口的车辆路径问题，记录最小的等待时间和路线生成过程中的最小延迟时间。在此基础上，国内外学者开始研究使用不同的算法求解时间窗约束的车辆路径问题；Xiao等[3]基于实际分析，将油耗率引入VRP，以最小化燃油消耗量为目标，提出了基于油耗的车辆路径问题的改进模型，并设计了改进的模拟退火算法进行求解；贺政纲等[4]针对当前物流配送系统中存在的车辆负载不均衡导致的物流配送质量和配送系统柔性下降这一现象，提出了考虑均衡车辆负载的多目标路径优化模型，既考虑了提高客户服务水平和员工公平性问题，又考虑了距离和不平衡度之间的关系；Tang[5]等考虑了物流运输途中载重动态变化对运行成本的影响，提出了基于载重成本的车辆路径问题，结合问题属性设计了一种分散搜索算法；Mirhosseini[6]研究了在不确定顾客需求状况下的VRP问题，顾客需求的不确定性有利于企业规划可靠的行车路线和配送计划，增加顾客的满意度;张文博等[7]针对动态需求下带时间窗的车辆路径问题，在最小化配送成本目标下，通过提升服务的准时性来改进顾客满意度，通过采用模拟退火法结合两阶段规划方法得到优化后的车辆路径配送方案。

关于循环取货模式的研究，通常是通过对所建立的循环取货模型进行仿真，以验证这一运作模式运用在某一企业中的可行性。杨浩雄等[8]结合路径优化、循环取货、JIT供应管理等相关理论基础，从供应链优化的角度，为汽车制造企业和零部件供应商提出了双循环集配零部件入厂物流模式；Kitamura等[9]以零部件入厂物流模式为研究对象建立了关于循环取货的理论框架，使用NuSMV模型检查器对该框架进行测试，通过分析其计算难度和算例结果，评价了其实行设计的切实性。关于循环取货路径的研究主要分为两个研究方向：一是关于模型改进的研究，如伊俊敏等[10]对某主机厂的零部件循环取货问题进行研究，在循环取货模型中加入软时间窗约束，根据主机厂各供应商的取货时间要求、零部件采购需求及地理位置建立了以车辆总行驶路径最短为目标函数的循环取货模型；朱玲等[11]提出将供应商集货需求拆分配送的改进数学模型，以总循环取货成本最小为目标函数，同时满足运输车辆容量限制和供应商取货时间窗限制，针对某条路径供应商供货量与车辆的剩余容量不匹配的情况，可以选择配送部分零部件，剩余的零部件可由其他路径的车辆进行配送，即每个零部件供应商可由多条路径访问，这对提高车辆的装载率减少运输成本具有重大意义。二是关于算法的改进研究，如曲琳璐[12]设计了改进遗传算法对循环取货问题求解，通过计算分析，将原有算法与改进遗传算法的求解结果进行比较，证明了改进遗传算法在处理循环取货路径规划问题的优越性；Jafari-Eskandari等[13]设计了粒子蚁群算法，解决了库存不确定情况下的车辆循环取货问题；Ohlmann等[14]先运用嵌套式禁忌搜索启发式算法对精益生产中的CFR问题进行优化，然后采用二元整数规划法设定供应商允许取货时间窗进行循环取货路径优化，实验结果证明了该两阶段算法的可行性。在低碳减排方面，Franceschetti[15]通过建立带有时间窗的VRP模型，发现通过设定时间窗使运输车辆避免交通拥堵，能够减少运输过程的CO2排放量；康凯等[16]考虑以碳排放量最小和客户满意度最大为目标函数，构建了基于碳排放的模糊约定时间车辆路径模型；Jabali等[17]构建了考虑时间、燃料消耗和CO2排放成本的VRPTW数学模型，并用禁忌搜索算法进行求解，最终发现通过权衡燃料和时间成本，限制车辆的运行速度可以减少总成本花费。

基于已有的国内外相关领域的研究成果，提出新的数学模型，是对车辆路径问题研究内容的补充和深化。虽然国内外学者对低碳VRP问题有所研究，但是很少有学者将低碳VRP与循环取货问题组合进行研究。本文将研究考虑低碳循环取货模式问题，以包括车辆运输成本、燃料成本和碳排放成本在内的总成本最低为优化目标，与常规的不考虑碳排放因素的零部件入厂物流问题进行对比，在一定程度上丰富了绿色车辆路径问题方面的研究范畴，具有一定的理论意义。

1 问题描述及模型构建

1.1 问题描述及假设

在传统的车辆路径优化基础上，加入了碳排放成本的约束，考虑低碳循环取货入厂物流的运作模式是针对目前汽车公司循环取货设计中存在的不足之处提出的合适的改进方案。问题的假设如下：

1) 路况。假设从配送中心到各供应商及各供应商之间都有可连通的行驶路径，不考虑实际影响道路状况的因素如红绿灯、道路管制、天气状况等，运输时间等于运输里程除以运输速度。

2) 供应商。各供应商的地理坐标及取货数量、时间窗、车辆服务时间已知，一个供应商只能被一辆运输车辆取货一次。

3) 物流配送中心。存在唯一的、地理坐标明确的物流配送中心，循环取货获得的所有零部件最终送至物流配送中心，车辆到达物流配送中心的时间没有限制。

4) 运输车辆。所有运输车辆的型号相同且确定， 参与循环取货作业的车辆足够多，所有车辆从物流配送中心出发最终返回到物流配送中心。所有车辆取得零部件的总重量不能超过其最大装载量，并且认为所有车辆均以相同速度匀速行驶。

5) 时间。车辆零部件循环取货作业在时间上为连续状态。

6) 碳排放。碳排放量的计算只考虑车辆油耗产生的CO2，其他情况下产生的CO2忽略不计。

1.2 参数和变量

参数设置：

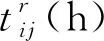
1.3 碳排放量的计算

运输车辆产生CO2的多少主要与运输车辆的油耗大小有关，且与之成正比关系。在最初的研究中，车辆油耗的计算方式比较简单，被认为只与运输车辆的行驶距离有关。然而，随着中外学者对这方面的研究不断加深，发现实际影响车辆油耗的因素有很多，主要分为交通因素、环境因素、运作因素、车辆因素以及驾驶因素等五大类，如表1所示[18]：

表1 车辆油耗影响因素表Table 1 Table of factors affecting fuel consumption of vehicles

根据不同的油耗影响因素可以建立不同的油耗计算模型，从而产生计算方法。根据国内外碳排放相关文献研究，车辆碳排放量与车辆油耗呈线性关系[19-21]且成正比，假设车辆油耗量为F，碳排放系数为λ，那么对应车辆的碳排放量E可表示为两者的乘积：

E=F×λ

常用的耗油计算模型主要有3种，瞬时油耗模型、四阶段油耗模型、综合油耗计算模型。本文选取运用普遍的综合油耗计算模型，从微观角度估算本文取货车辆在循环取货过程中的油耗量。

假设货运车辆在一段长度为dij(从i到j的距离，单位：km)的路径以平均速度v(m/s)行驶，运用综合油耗计算模型，车辆在该路段行驶过程中产生的油耗量为

Ft=φkNVd/v+φP车γd/v

其中：φ为燃气质量比，k为车辆发动机摩擦系数，V(cc)车辆发动机排量，N(r/min)为发动机的转速，γ为常量，P车(kw/km)为运输车辆单位距离行驶需要的总功率，在不考虑功率损失的条件下，其可表示为

P车=P牵/ηtf

ηtf为运输车辆的传动效率，P牵为车辆单位距离行驶需要的总牵引功率，P牵经过简化处理可表示为

P牵=(Mvα+βv3)/1 000

其中：M为运输车辆的总重(kg)；在行驶道路没有任何坡度的情况下，α=a+gsinθ+gCrcosθ，其中a为车辆加速度(m/s2)，g为重力加速度(m/s2)，Cr为滚动阻力系数；β=0.5CdAρ，其中Cd为空气阻力系数，ρ为空气密度(kg/m3)，A为运输车辆前部的表面积(m2)。

将P牵=(Mvα+βv3)/1 000带入Ft=φkNVd/v+φP车γd/v，得出运输车辆在(i，j)路径上的能源消耗量为

Ft，ij=λ(kNV+Mγαi，jv+βγv3)dij/vij

式中：λ=φ/kψ，γ=1/1 000ηtfη都是常量，ψ为将燃料单位从g/s转换为L/s的转换因子。除了速度与载重外，其他参数的数值都是固定的，具体数值如表2所示。

表2 模型参数值表Table 2 Model parameter values table

1.4 数学模型

在以上决策变量和计算符号的基础上，建立如下的循环取货模型：

(1)

(2)

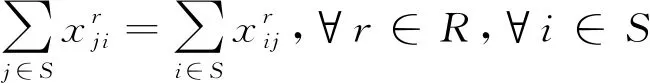
(3)

(4)

(5)

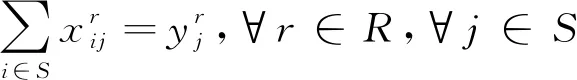
(6)

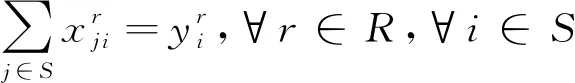
(7)

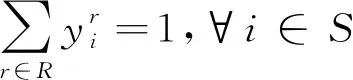
(8)

∀r∈R，∀j∈S且j≠0

(9)

(10)

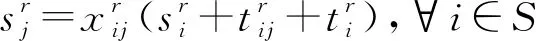
(11)

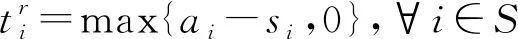
(12)

si≤bi，∀i∈S且i≠0

(13)

其中：式(1)以所有循环取货车辆行驶的总路径长度最小为目标函数；式(2)以车辆循环取货总成本为目标函数，其中包括车辆油耗成本、碳排放成本以及固定行驶成本；式(3)表示进入和离开各供应商处的车辆数目相等，确保车辆在取货后离开供应商处；式(4)和(5)表示车辆取货路径的起点与终点相同，确保车辆的循环取货路径形成一个完整的回路；式(6)(7)(8)表示每一个零部件供应商只被分配到一条循环取货路径中；式(9)表示每个供应商有且只被一辆车访问一次；式(10)保证车辆在路径r上的取得的零部件重量之和小于该车辆的最大载重量；式(11)表示在路径r上，车辆抵达供应商j处的时间为车辆抵达供应商i处的时间加上车辆服务时间加上车辆从供应商i到供应商j的行驶时间；式(12)与式(13)确保车辆在供应商i允许的取货时间内到达供应商i处。

2 模型求解

2.1 循环取货作业遗传算法设计

(1) 染色体编码。考虑低碳的循环取货作业可编织成一条1+i+r的染色体，可表示为

(0，1，2，…，n，0，n+1，n+2，…，m， 0，…，0，m+1，m+2，…，i，0)

其中将物流配送中心编号为自然数0，用整数1—i对i家供应商进行编号，按照随机次序i家供应商将形成一条长度为i的染色体；按照估算的车辆数，r随机生成r-1个断点，0作为分隔符插入每个断点的开头与结尾处，从而形成r条循环取货路径。这条染色体的结构可以看作运输车辆1从配送中心0出发，依次访问供应商1，2，…，n后返回配送中心，运输车辆2从配送中心0出发，依次访问供应商1，2，…，m后返回配送中心，直到完成对所有供应商的取货任务。以一条可行线路编码为037501840620的染色体为例，所形成的车辆路径分别为

路径1 物流配送中心0→供应商3→供应商7→供应商5→物流配送中心0

路径2 物流配送中心0→供应商1→供应商8→供应商4→物流配送中心0

路径3 物流配送中心0→供应商6→供应商2→物流配送中心0

(2) 种群初始化。一般来讲，初始种群规模通常会根据实际问题中染色体长度在30～200间浮动。本文采取随机方式生成规模为150的初始种群。

(3) 适应度函数。由于本文的目标函数是总路径和总成本最小值问题，故而将取目标函数的倒数作为适应度函数，即fk=1/minZ。

(4) 选择算子。常见的遗传算法选择策略有：适应度比例选择策略、适应度排名选择策略、最佳个体保存选择策略、局部竞争机制选择策略。循环取货作业过程的遗传算法，一方面考虑算法选择的全局性，避免单纯的局部选择；另一方面考虑遗传算法的运行速度，提高运行效率。因此，本文采用混合选择策略，即综合后两种选择策略。

(5) 交叉算子。本文选择应用最广泛的部分匹配交叉法进行交叉操作，详细流程如下：任意选择两条染色体(对于本文来说就是循环取货子路径)A和B，在A和B上随机得到两个交叉点，找出A和B的匹配区域并进行互相交换，得到A′和B′，对A′和B′匹配区域以外区域的基因进行交叉，得到两条新的染色体(取货路径)A″和B″。

(6) 变异算子。针对本文考虑低碳的循环取货路径优化问题，将基于局部竞争机制选择的染色体进行逆转、对换和插入变异。

(7) 终止条件。遗传算法中常用的终止条件有两种，一是达到初始设定最大的迭代次数值时停止运算，二是同一结果连续若干次没有明显变化时停止运算，则算法输出最优解。

2.2 Matlab求解

本文以DF汽车公司为对象，利群物流有限公司为配送中心，对参与DF汽车公司零部件循环取货的32家供应商进行零部件物流运输。

运输车辆从物流配送中心出发，因大多数供应商地处开发区，车流量较小，故不考虑交通堵塞的情况。假设运输车辆以40 km/h的速度匀速行驶，每辆运输车辆的固定发车成本为180元/辆，单位距离运输成本为2元/km，运输车辆的最大载重量为10 t，大气污染物按每污染当量计税为1.2元/kg(参照2016年我国底发布的《环境保护税法》)，燃油单价为5.6元/L(2016年柴油报价)，其他参数见表3：

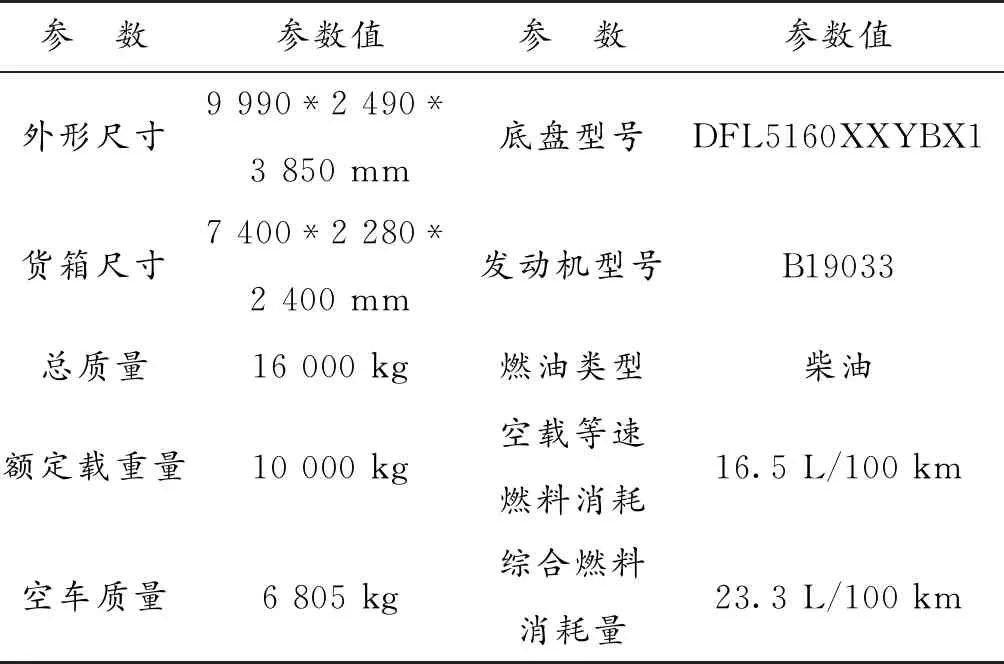
表3 循环取货运输车辆参数表Table 3 Transport vehicle parameter list of milk-run route

基于Matlab2014a的环境下，本文设定遗传算法中的各项参数如下：初始种群P(0)数目取100，最大迭代次数取500次，变异概率Pm取0.1，交叉概率Pc取0.6。

2.3 不考虑碳排放的循环取货模型求解

当不考虑碳排放成本，仅考虑车辆行驶最短距离时，具体路径优化结果如表4所示。

表4 不考虑碳排放的循环取货的数据结果Table 4 The data results of milk-run route not considering carbon emission

2.4 考虑碳排放的循环取货模型求解

当考虑碳排放成本，以车辆运行成本和碳排放成本之和最小为目标函数时，具体路径优化结果如表5：

表5 考虑碳排放的循环取货的数据结果Table 5 The data results of milk-run route considering carbon emission

3 结果与分析

上节已对不考虑碳排放的循环取货模型和考虑碳排放的循环取货模型进行求解，分别计算其对应的路径长度、碳排放量和成本，并对结果进行对比分析。为方便分析讨论，将两种优化模型所得的路径对应的距离、碳排放量、成本等指标对比分析(表6)，可以得出考虑碳排放的循环取货模型的循环取货路径为6条，与不考虑碳排放的循环取货模型的计算结果相同。

表6 两种情况下的算例运算结果Table 6 Operation results of two examples

通过对具体循环取货路径分析，不考虑碳排放的循环取货模型的路径长度为998 km，循环取货总成本为4 323.1元，碳排放量为463.23 kg；考虑碳排放的循环取货模型的路径长度为1 036 km，循环取货总成本为4 255.25元，碳排放量为385.11 kg。由此可知，考虑碳排放的循环取货模型比不考虑碳排放的循环取货模型路径总长增加了3.8%，但总成本比后者减少了1.6 %，碳排放量减少比例为12.37%。就环境影响而言，考虑碳排放的循环取货模型减少了对环境的影响，验证了模型的可行性。

4 结 论

碳减排下以总路程最小为目标函数的循环取货模型生成的循环取货路径虽然增加了运输路线长度，但降低了汽车的油耗量。近年来我国油价不断上涨，随着“高油价时代”到来，汽车油耗量的降低必然会减少油耗成本，所以采用考虑低碳循环取货模型生成的取货路径不仅能为公司带来经济效益，而且能为社会带来环境效益，实现企业和社会的共赢。

随着低碳经济的发展，政府部门会采用越来越多的碳减排政策来减少企业的碳排放量。为了保障碳排放目标的实现，碳排放成本为政府测算的外部成本，碳减排下的循环取货模型将外部成本转化为汽车企业的内部成本，这为促使企业实施低碳物流提供了决策依据。对企业而言，在碳交易价格较低的情况下，碳成本与总成本之比相对较小，企业会忽视对低碳经济的发展；当碳交易价格较高时，碳成本对企业总成本有较大的影响，企业将会重视低碳经济的实现。对政府而言，政府可以通过提高碳交易价格的方式促使企业发展低碳物流，减少碳排放对环境的影响。