疫情期间模糊随机应急物资库存问题*

曾 陈 锐

(重庆师范大学 数学科学学院， 重庆 401331)

0 引 言

新冠肺炎疫情这种突发性的公共卫生事件由于发生的突然性、时间上的紧迫性使得供应的生活物资以及医疗物资跟不上需求，专项医疗人员更是稀缺。经济和生活的息息相关致使物价飞涨，因此医疗物资以及生活物资在此时必须得供应上，疫情的持续时间是不可控的，所有常规的政策在此时也会做出相应调整，比如道路交通以及物资配送，如何利用模型策略增强应对突发事件来临的反应能力已成为一个重要课题。

董银红等[1]考虑受益最大风险最小的应急救援物资运输模型；王芹等[2]考虑突发事件影响下应急物资的最优订货量及零售商的利润最大；这两个文献主要考虑零售商的角度风险小收益大。李健等[3]构建了应急物资调运的一般系统动力学模型，并说明了政府对突发事件信息的反应速度和应急物资调度能力起到了决定性作用；缪成等[4]综合了多货物多起止点网络流问题与多种运输方式满载车辆调度问题，基于拉格朗日松弛法解决问题；文献[3-4]结合了网络流问题以及多种运输方式，考虑因素过多使得模型较为复杂。高咏岩[5]通过分析需求的不确定性和库存管理控制策略，建立了经济订货批量模型(EOQ)，完成了精确库存管理系统设计；李卓群等[6]建立了受不确定需求影响的供应链库存系统动态模型，并考虑库存成本和服务水平两个系统性能评价指标进行仿真实验，得到不同提前期不同需求模型下的最优库存策略域；邱若臻等[7]考虑需求分布分别隶属于区间和椭球不确定集两种情形，运用对偶理论将多周期库存鲁棒优化模型转化为易于求解的凸规划问题；此研究考虑了需求不确定、库存成本以及服务水平，但所涉及的模型理论在计算时较为复杂。

结合新冠肺炎疫情的特殊性和应急物资的特点，在不同的需求下满足一定的服务水平考虑总损失最小时的订货量，运用三角模糊数以及可信性理论建立总损失最小的库存模型，由于各地区受疫情影响的程度不同，因此要根据不同需求制定不同方案，在最短的时间内以最高效的方式最大程度地满足被疫情困扰的地区对物资的需求。各个企业也需要有相应的应急管理策略，因此凸显了对企业应急物资库存的研究具有重要的理论意义和现实意义。

1 新冠肺炎疫情应急物资需求特点分析

新冠肺炎主要的传播途径是经呼吸道飞沫和密切接触，且在相对封闭的环境中长时间暴露于高浓度气溶胶的情况下，存在经气溶胶传播的可能。人们通常是不具有对新型病毒的抵抗力，根据受染人群可分析得到此结论，且与前面发生的SARS病毒作对比会发现新冠病毒的传播力更快，传染人群更普遍，但其死亡率要低于SARS。

应急物资是指为应对严重自然灾害、突发性公共卫生事件、公共安全事件及军事冲突等突发公共事件应急处置过程中所必需的保障性物质[8]。白窦萍[9]对突发性事件中快速消费品的应急物流从灾前的储备准备阶段到灾后如何有效快速送抵到受灾区进行了合理的分析；张翔等[10]为切实提高企业安全生产能力，探讨了企业安全生产应急管理存在的问题并提出相应对策；张晶等[11]提出要建立科学合理的应急物资储备模式，科学应急。许许多多文献都在研究应急物资的储备以及库存的问题，如果不防患于未然，将会对国家和社会造成不可估量的重大人员伤亡和财产损失。

结合此次新冠肺炎疫情，其发生在临近春节的时期，以及其具有潜伏期且潜伏期无明显症状，导致春运高峰期病毒携带者四处分散并在不自知患病的情况下传染与其接触者。因此，无论是患病者还是未患病者，都需要口罩、手套等消耗物资，随着患病者的增加以及春节大部分工厂休假，群众出现恐慌的情绪并开始疯抢物资，使得供应量远远小于需求量。疫情信息短时间内比较匮乏，信息具有很强的不完备性以及滞后性，很难精准预测物资需求，该阶段的应急救援物资多依据历史相似事件的数据、决策者经验以及疫情严重程度等开展，具有一定的不确定性。随着病情的缓解、国家政策的调控，物资也得到缓解，具有时效性。由国家交通运输部发布的消息来看，尽管疫情期间通行受限，但对于应急物资是无障碍通行，没有了平时的交通拥堵，运输效率达到最高，运输成本达到最低。

2 疫情期间应急物资库存模型

疫情是不可预测的，是概率事件，模糊性和随机性会同时存在于模型中，所以根据需求模糊且随机建立相应的应急物资库存模型。

2.1 模糊以及可信性理论

定义1[12]模糊理论是指用到了模糊集合的基本概念或连续隶度函数的理论。

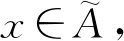
(1)

三角模糊数的隶属函数如图1所示。

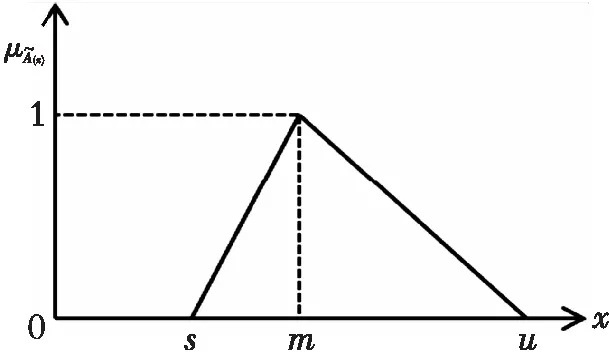
图1 三角模糊函数的隶度函数Fig. 1 The membership function of the triangular fuzzy function

定义3[13]可能性测度：假设Θ为非空集合，P(Θ)表示Θ的幂集，称定义在P(Θ)上的集函数Pos为P(Θ)上的一个可能性测度，若满足以下3个公理：

公理1Pos{Θ}=1。

公理2Pos{Ø}=0。

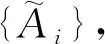
定义4[14]在可能性空间(Θ，P(Θ)，Pos)上，还可以定义可能性测度Pos的对偶测度，即必要性测度Nec为

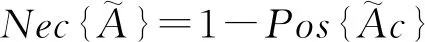
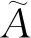
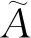
由式 (1) 以及上述定义可求得三角模糊变量对应的可信性测度表达式为

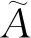
(2)

2.2 模型的建立与分析

2.2.1 符号说明与条件假设

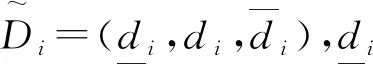
表1 变量的符号说明Table 1 Symbol explanation of variables

另作假设如下：应急物资的需求概率分布已知， 满足一般规律并服从任何分布，周期单一，无补货提前期，持有成本在物资剩余时才存在。

2.2.2 模型的建立及求解

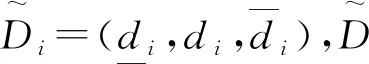
建立需求模糊随机的应急物资库存模型

目标函数为库存损失最小的期望；第一项为多余的物资所产生的损失；第二项为估计的物资跟不上需求而从其他地方调运物资所产生的额外成本；最优订货量要满足一定的服务水平，根据应急物资的特点在有效率的情况下损失尽可能低。

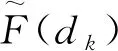
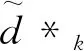
得：

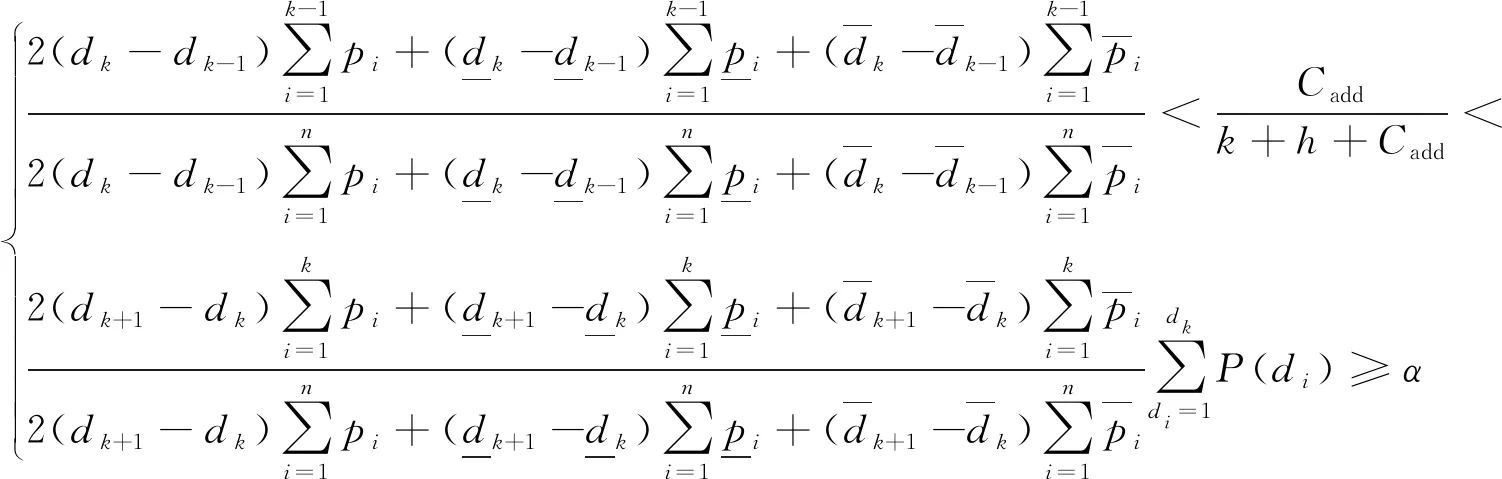
3 算例分析

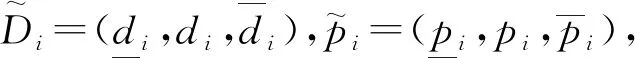
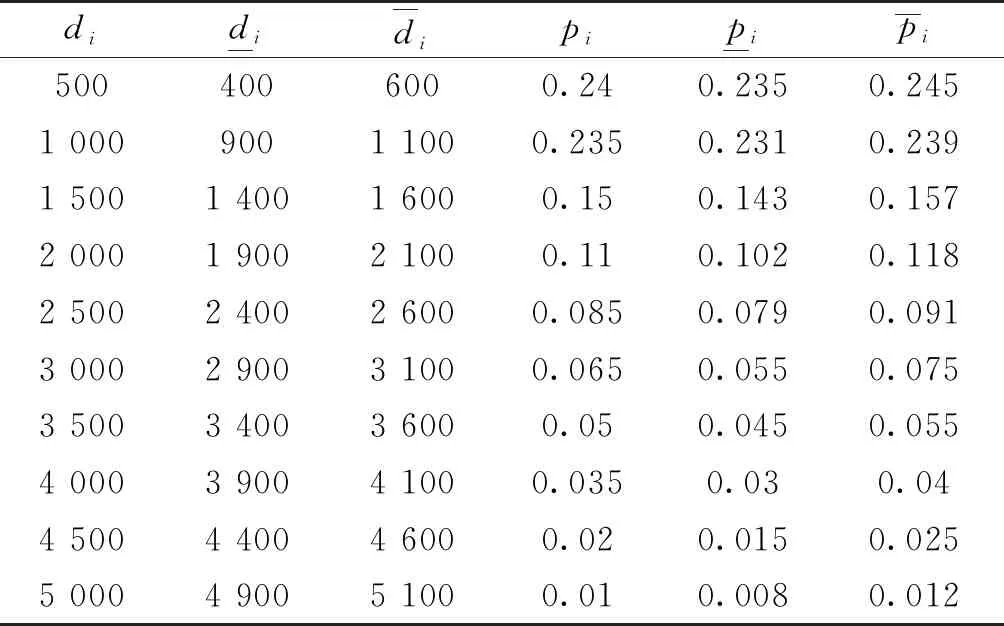
表2 低成本应急物资需求分布Table 2 Demand distribution of low-cost emergency supplies

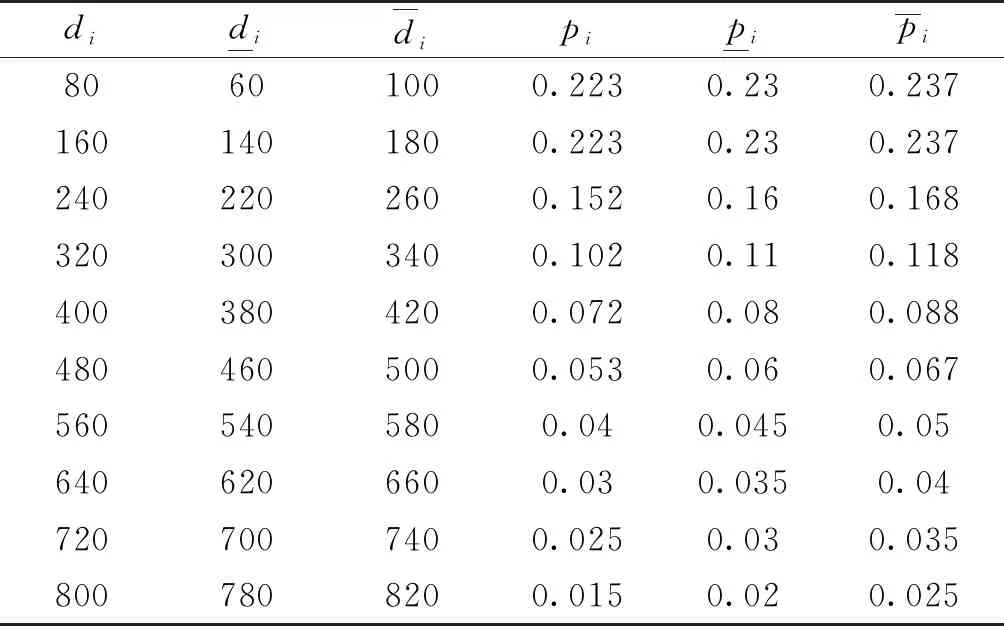
表3 高成本应急物资需求分布Table 3 Demand distribution of high-cost emergency supplies

求解过程如下：

令变量A和B分别为

通过MATLAB软件进行计算求解得出表4、表5，MATLAB算法如下(以低成本为例)：

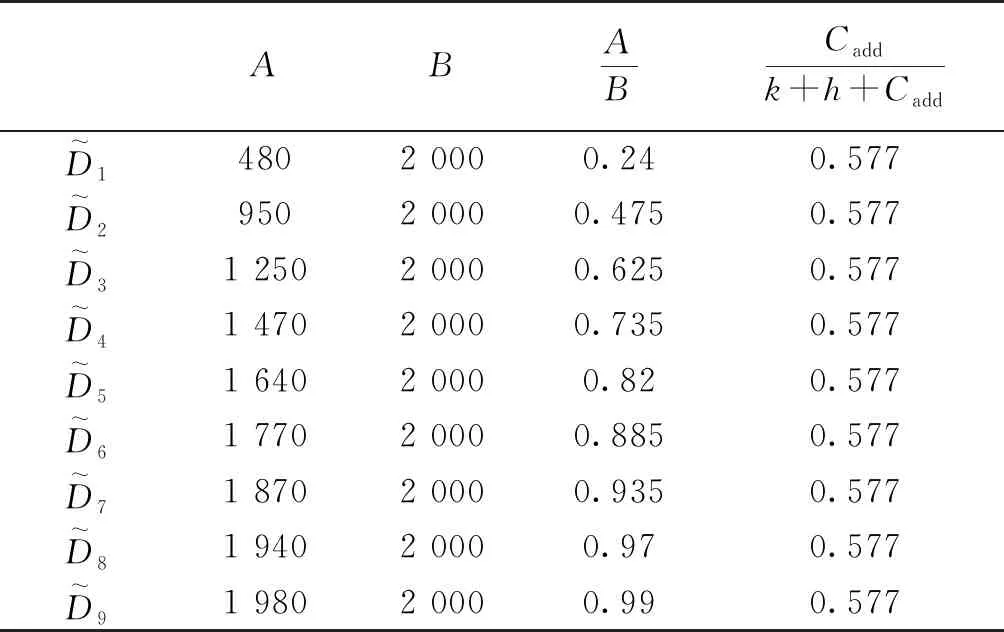
表4 低成本物资分析结果Table 4 Low-cost material analysis results

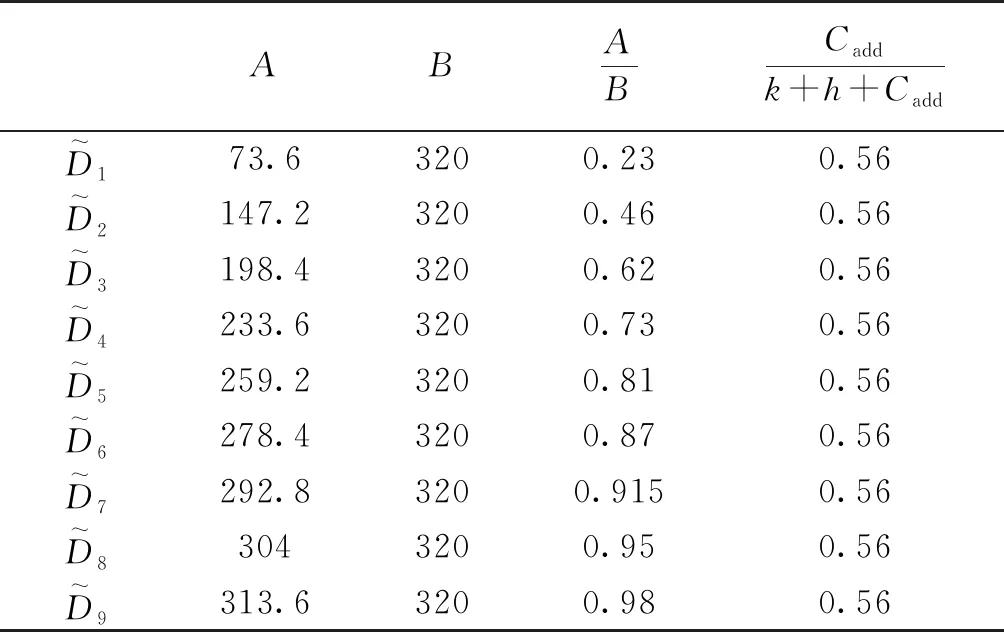
表5 高成本物资分析结果Table 5 High-cost material analysis results

步骤1 计算A，B值：

a=zeros(1，9)；b=zeros(1，9)；c=zeros(1，9)；

D=[500，10 00，1 500，2 000，2 500，3 000，3 500，4 000，4 500，5 000]；

A=[400，900，1 400，1 900，2 400，2 900，3 400，3 900，4 400，4 900]；

C=[600，1 100，1 600，2 100，2 600，3 100，3 600，4 100，4 600，5 100]；

PD=[0.24，0.235，0.15，0.11，0.085，0.065，0.05，0.035，0.02，0.01]；

PA=[0.235，0.231，0.143，0.102，0.079，0.055，0.045，0.03，0.015，0.008]；

PC=[0.245，0.239，0.157，0.118，0.091，0.075，0.055，0.04，0.025，0.012]；

forj=1：9

a(j)=2*(D(j+1)-D(j))*sum(PD(：，1：j))+(A(j+1)-A(j))*sum(PA(：，1：j))+(C(j+1)-C(j))*sum(PC(：，1：j))；b(j)=2*(D(j+1)-D(j))*sum(PD(：，1：10))+(A(j+1)-A(j))*sum(PA(：，1：10))+(C(j+1)-C(j))*sum(PC(：，1：10))；c(j)=a(j)/b(j)；

end

print(a)

步骤2 计算总损失：

EA=zeros(1，9)；ED=zeros(1，9)；EC=zeros(1，9)；

D=[500，1 000，1 500，2 000，2 500，3 000，3 500，4 000，4 500，5 000]；

A=[400，900，1 400，1 900，2 400，2 900，3 400，3 900，4 400，4 900]；

C=[600，1 100，1 600，2 100，2 600，3 100，3 600，4 100，4 600，5 100]；

PD=[0.24，0.235，0.15，0.11，0.085，0.065，0.05，0.035，0.02，0.01]；

PA=[0.235，0.231，0.143，0.102，0.079，0.055，0.045，0.03，0.015，0.008]；

PC=[0.245，0.239，0.157，0.118，0.091，0.075，0.055，0.04，0.025，0.012]；

K=10；h=1；Cadd=15；

forj=1：9

EA(j)=(K+h)*sum(A(j).*PA(：，1：j)-C(：，1：j).*PC(：，1：j))+sum(Cadd*(A(：，j+1：10).*PA(：，j+1：10)-C(j).*PC(：，j+1：10)))；ED(j)=(K+h)*sum(D(j).*PD(：，1：j)-D(：，1：j).*PD(：，1：j))+sum(Cadd*(D(：，j+1：10).*PD(：，j+1：10)-D(j).*PD(：，j+1：10)))；EC(j)=(K+h)*sum(C(j).*PC(：，1：j)-D(：，1：j).*PD(：，1：j))+sum(Cadd*(C(：，j+1：10).*PC(：，j+1：10)-C(j).*PC(：，j+1：10)))；

End

4 结论与讨论

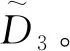
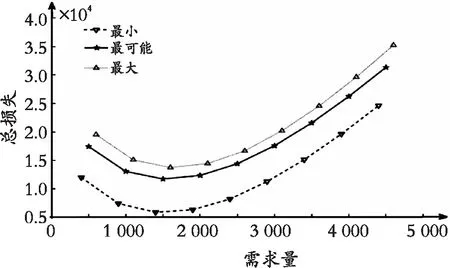
图2 不同需求下总损失变化曲线Fig. 2 Change curve of total loss under different demand

图3 不同需求下服务水平变化曲线Fig. 3 Service level change curve under different needs

根据疫情这个特殊时期物资的紧急突然性以及需求的不确定性，结合了模糊三角数与可信性理论设立了库存总损失最小的目标函数来大致确定最优订货量。由算例可看出总损失最小时其订货量的值不一定可行，还必须得达到一定的服务水平，疫情期的物资要求首要是效率高，其次再考虑其成本问题。由于模糊数是一个大致的范围，不同的事件其物资需求量也不同，要想低损失且效率高就要缩小物资的需求范围，才能够更好地管理应急物资的库存。在当今社会，发展迅速的同时也会面临更多的突发事件，在不确定需求下采用模糊数及可信性理论建立的总损失最小库存模型有一定的实用性和参考价值。