一道美国数学竞赛题的推广
2022-10-10 08:26:18广东省深圳市深圳中学518001邱际春
中学数学研究(江西) 2022年10期
广东省深圳市深圳中学 (518001) 邱际春
2016年AMC12B中第20题是如下组合计数问题:
原题呈现A set of teams held a round-robin tournament in which every team played every other team exactly once. Every team won 10 games and lost 10 games; there were no ties. How many sets of three teams {A,B,C} were there in which A beat B, B beat C, and C beat A?
(A)385 (B)665 (C)945
(D)1140 (E)1330
原题译文若干支球队进行循环赛,即每组球队与其他球队各进行一场比赛.已知每组球队赢了10场比赛且输了10场比赛,每场比赛中不出现平局.在三支球队组成的集合{A,B,C}中,A赢了B,B赢了C,C赢了A,请问有多少个这样的集合?
(A)385 (B)665 (C)945
(D)1140 (E)1330

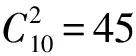
显然,这种情况是可能的:将各球队围成一个圆圈,并且按顺时针的顺序使得每支球队均打败接下来的10支球队.
评注:此题有一定难度,关键是对题目的理解的把握,如果能从题干中获知循环赛的球队数,那么根据循环赛的规则就不难得到本题答案为A.
若考虑将每组球队输或赢的比赛场数推广至n场,则原题可作如下初步推广:


若将原题中满足给定条件的三支球队组成的集合{A,B,C}推广至k支球队组成的集合{a1,a2,…,ak},则可进一步得到下面的推广2:
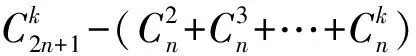
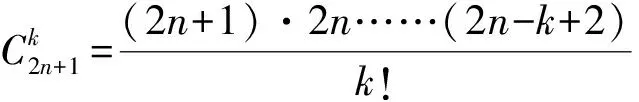
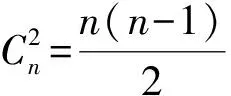
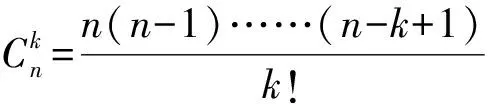
猜你喜欢
中等数学(2022年4期)2022-08-29 06:27:14
发明与创新·小学生(2022年6期)2022-05-22 08:20:02
中等数学(2020年7期)2020-11-26 08:03:46
中等数学(2020年4期)2020-08-24 08:08:38
中等数学(2019年5期)2019-08-30 03:52:22
数学小灵通(1-2年级)(2018年6期)2018-06-28 03:15:38
考试周刊(2017年16期)2017-12-12 08:31:22
文学教育(2016年26期)2016-04-03 20:03:11
初中生学习·低(2015年6期)2015-05-30 10:48:04
创新作文·初中版(2014年8期)2014-10-09 03:04:11

