一道平面向量题的解法探究

重庆市铜梁二中 (402560) 李 波 周渝川

在浙江省的高考和模拟考试中，平面向量往往作为填空压轴题出现.这类题目虽短小精干，却解法丰富多样、不失经典.

一 解法探究

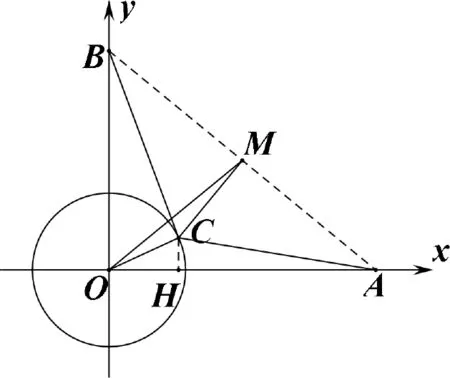
图1

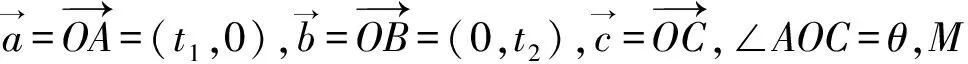
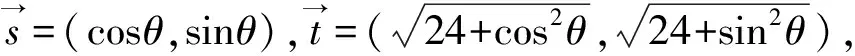
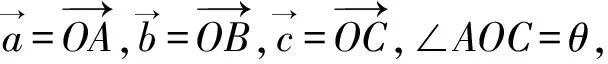
评注：解法2运用辅助线，简化运算.

评注：先将目标平方，把问题转化成求数量积的范围，再把数量积用函数表示，最后用柯西-布捏科夫斯基不等式放缩求解.“见模平方”是处理向量的模有关问题的常见方法.

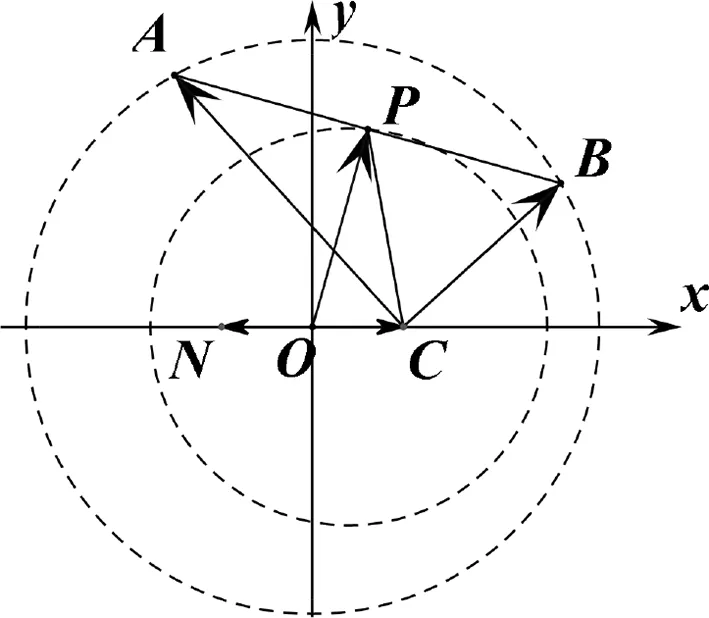
图2

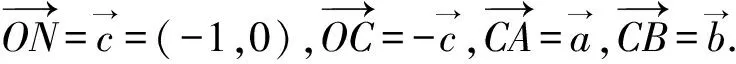
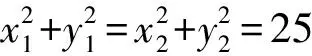
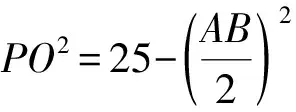
评注：建立直角坐标系，首先将目标转化成动点到定点的距离，解法4充分利用“点A,B在圆x2+y2=25上”及消元法，求得P的轨迹，运算量偏大；解法5用到了这样一个圆的模型：平面上到两定点的距离的平方和为定值的点的轨迹是圆，十分简洁.

图3

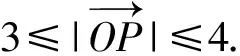
评注：解法6和解法4、解法5的共同点在于利用“隐圆”的性质解题，计算量较小，关键是利用了矩形的一个性质.

由解法6，我们容易得到一般规律，即：

进一步可得：

向量兼有几何和代数特征，是联系三角、几何、代数的纽带.处理向量问题所用的技巧和方法十分丰富，如：转化、数形结合、不等式等，几乎涵盖了整个高中数学的思想方法，这有利于从整体上把握数学知识.因此，在处理向量问题时往往要将几何直观和代数运算结合使用，充分联想，多方位考虑问题，提高思维品质，这也是数学核心素养的要求.