注重解题通法，加强变式探究——以一道高二期末联合测试题为例

重庆市忠县中学校 (404300) 张 侣

圆锥曲线中的最值、范围问题是高考或各地模拟考试中常见的热点问题.此类问题考查知识点多，涉及范围广，形式灵活多变，思维视角多样，利于考生的选拔与区分，可以很好考查学生的数学知识、思想方法和能力，深受命题者青睐.

一、题目呈现

(1)求曲线C的方程；(2)若点M在曲线C上，过点M且垂直于OM的直线交C于另一点N，点M关于原点O的对称点为Q，直线NQ交x轴于点T，求|QT|·|TN|的最大值.

试题评析：第(1)问以过A,B定点的两条动直线斜率乘积为定值入手，探究两条直线交点的轨迹方程，较为简单，注重考查数学的基本知识，基本概念.第(2)问考查直线与圆锥曲线的位置关系，弦长表示，最值问题.试题立足通性通法，注重数学本质，设计合理，解法多样，考查了学生直观想象、逻辑推理、数学运算等数学核心素养，有很好的教学引导作用.

二、解法研究

点评：联立直线与椭圆方程，借助韦达定理即可求出x1x2+y1y2，结合直线MQ与MN的垂直关系，获得了kMQ=2kMN，进一步得到参数m与t的关系，借助弦长公式得到|QT|·|TN|的表达式，再根据基本不等式求最大值.

点评：从圆锥曲线点差法的思想角度入手，探寻直线MN与NQ的斜率乘积为定值，结合直线MQ与MN的垂直关系，获得了kMQ=2kMN.根据直线MN与NQ方程求点N的纵坐标，借助弦长公式得到|QT|·|TN|的表达式，再根据基本不等式求最大值.

三、变式拓展

结合以上原问题的破解过程，改变问题的设问方式，获得以下几个变式问题.

变式1 若点M在曲线C上，过点M且垂直于OM的直线交C于另一点N，点M关于原点O的对称点为Q，直线NQ交x轴于点T，求证：直线MT垂直于x轴.

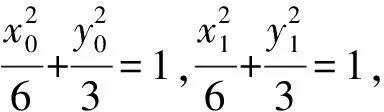
变式2 若点M在曲线C上，点M关于原点O的对称点为Q，MT⊥x轴，垂足为T，连接QT并延长交C于点N.求证：kMQ·kMN为定值.

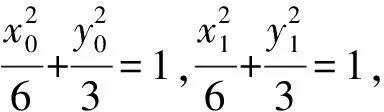
变式3 若点M在曲线C上，过点M且垂直于OM的直线交C于另一点N，点M关于原点O的对称点为Q，求△MQN面积的最大值.

四、解后反思

著名数学家波利亚曾说：“解题就像采蘑菇一样，采到一颗蘑菇以后应向周围看看，可能还会有意外收获”.因此，对试题的变式、引申、拓展探究就显得尤为重要，所以教师在教学过程中要重视对试题的研究，从中发现问题，提出问题，再类比进行探究和拓展，以不同角度，不同方式进行解决问题，真正达到“求解一个题，拓展一类题，变式一片题”的最终目的，促使学生真正养成良好的数学思维品质和解题能力，进而提升数学核心素养.