傅里叶级数展开式在水轮发电机组安装中的应用

黄 飞

（中国水利水电第十六工程局有限公司机电制造安装分公司，福建 福州 350019）

0 前言

在水电站的水轮发电机组设备安装过程中，常常遇到圆度检查，比如止漏环、转子和定子等；同轴度检查，比如座环与转轮室，座环与底环（下止漏环），转轮止漏环与水轮机主轴，发电机机架与底环，定子铁心与底环等；偏心值检查，比如转子磁轭偏心值；机组轴线摆度检查，比如确定轴线最大的摆度值和方位；导轴承瓦间隙调整，比如按机组轴线检查结果，匹配每块瓦的间隙。本文着重介绍正弦函数的傅里叶级数展开式，并将此公式应用到电站设备安装过程中对同心度、偏心值、机组轴线摆度值的计算，测量数据的正弦曲线拟合。

正弦曲线方程式：f（t）=Asin（ωt+φ）+C

式中：

A——幅值

ωt+φ——相位角，以ω角速度运动t时间后所夹的角度。

t——时间变量

ω——角速度，，T为一个周期的时间

φ——初相角

C——常数，在X-Y直角坐标系上则为正弦曲线在Y轴上的偏移值。

1 傅里叶级数展开式与正弦曲线的关系

从高等数学可知，周期为T（T=2π）的周期函数f（x）=Ansin（nωx+φn）+C可以用傅里叶级数来表示，记为

傅里叶系数ao，an，bn

假定周期函数f（x）的基波一个周期内有N个采样点，用傅里叶级数展开式的系数离散化得到：

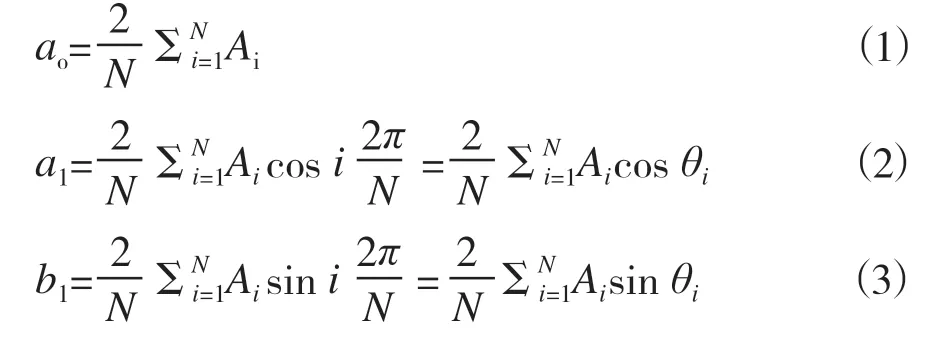
式中：

Ai——为基波一个周期内第i个采样的幅值

N——周期2π的基波采样总数目

i——采样点，i=1，2，3，…，N

θi——采样点与采样起始点的夹角

Ansin（nωt+φn）=ancosnωt+bnsinnωt可转化为Ansin（nωt+φn）=ansin（nωt+90）+bnsinnωt，用复指数表示上述等式，即Anejφn=anej90°+bnej0°，向量图见图1。

图1 正弦曲线基波的复指数向量图

由 此，函 数f（x）基 波 的 复 指 数 等 式A1ejφ1=a1ej90°+b1ej0°。

A1ejφ1的模为

向量A1ejφ1与向量a1ej0°的夹角

由 于tan-1的值域是没有完整反映f（x）的初相角φ值域范围（0～2π），因此需要根据b1值，判断φ在X-Y坐标系所处象限位置，进行相应调整，即当b1＜0时，则φ=π+φ1；当b1＞0，则φ=φ1。

通过上述分析，正弦曲线方程式f（θ）=Amsin（θ+φ）+C以2π为周期的基波方程式的各项系数Am、φ、C为：

初 相 角φ，当b1＜0时，则φ=π+φ1；当b1＞0，则

2 转子偏心值计算

以某个水电站的1号转子圆度测量数据为例，计算转子整体偏心值。

2.1 转子整体的偏心值要求

GB 8564-2003规范要求：机组转速300≤ω＜500时，偏心值e≤0.15 mm。

2.2 磁轭测量数据分析

1号机组转子磁极挂装后的圆度数据见表1。

转子共14个磁极，将同一个磁极的半径取平均值，利用傅里叶级数展开式的离散化公式，转子偏心值e按公式（4）计算。

因此，转子整体偏心值e=0.02 mm。

表1 磁极挂装后转子半径测量数据

3 水轮机导水机构同心度计算

以某个水电站的1号机组导水机构预装为例，计算座环与底环的同轴度。

3.1 导水机构预装要求

导水机构预装前，测量座环镗口圆度以确定机组中心；按座环镗口测定后给出的中心测点安装底环；底环的止漏环中心作为机组基准中心。

GB 8564-2003规范要求：止漏环的同轴度小于0.15 mm。

3.2 底环测量数据分析

1号机组的座环和底环的半径测量数据见表2。

利用傅里叶级数展开式的离散化公式（2）、（3）计算出座环上膛口的轮廓圆中心坐标（x1，y1）。

利用傅里叶级数展开式的离散化公式（2）、（3）计算出底环止漏环平均各环的轮廓圆中心坐标（x2，y2）。

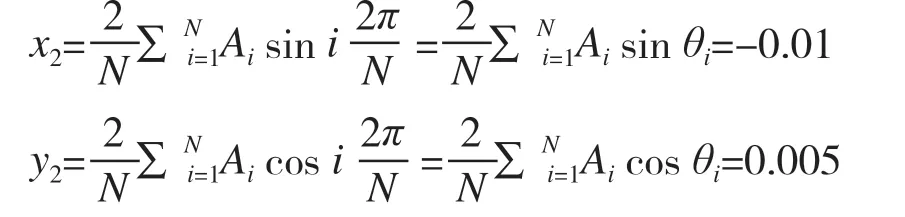
由此，底环止漏环相对于座环上膛口的偏心值

则底环止漏环与座环上膛口的同轴度偏差e=0.052 mm。

表2 底环止漏环的半径测量数据

4 机组轴线检查的数据分析和导轴承瓦间隙调整

在国内，机组轴线检查通常在轴线检查部位进行等角8点均匀等分，并在X、Y方向各架设百分表进行数据测量。在绝大多数情况下，机组轴线最大摆度点不可能落在我们预先标记的等分点上，因此，直接用测量数据求取机组轴线最大摆度值，常常小于机组轴线真实的摆度值，势必会影响到轴承瓦间隙准确调整，进而造成导瓦受力不均衡，瓦温差值大。

以某个水电站机组轴线检查为例，机组型式为半伞式，将测量数据采用曲线拟合方法进行分析，可以准确判断机组轴线最大摆度值和方位角，为导轴承瓦间隙匹配提供准确数值。

4.1 机组轴线检查数据

表3 机组轴线检查记录

4.2 拟合曲线

以水导X方向的盘车数据为例。利用公式（4）、（5）、（6），求取函数f（θ）=Amsin（θ+φ）+C各项系数为：

幅值Am=0.030 9

初相角φ，b1＜0时，则φ=π+φ1，即φ=269.85°

常数C=0.077 5

水导的实测值曲线与拟合曲线见图2。

图2 水导的实测值曲线和拟合曲线图

5 结束语

在机组设备安装过程中，运用傅里叶级数展开式，可以从繁杂的数据中归纳出准确的答案。上述例子的运用，可以为类似机电设备安装数据的分析提供借鉴。