主题教学观念下对“预备知识”的理解与教学

【摘 要】 为做好初高中衔接，课程标准将“预备知识”作为主题一，人教社A版数学教材构建了两章教学内容.笔者以集合为基础重构了“预备知识”的思维路径，并提出了主题教学观念下的教学实践方案与实施案例.

【关键词】 主题教学;预备知识;教学实践

“核心素养”指新时代的公民必须具备的人格品质及其关键能力，是落实“立德树人”的重要标尺.落实课程目标与培养学生素养的重要载体和途径是教学，要与传统“逐个”知识点的“了解”“识记”“理解”为目标的教学相区别，其关键在于实施“主题教学”.主题教学设计倡导将教学内容置于主题整体内容中去把控，更多地关注教学内容的本质、蕴涵的思想以及学生素养的培养[1]，由此教师基于学科素养，思考怎样描绘基于一定目标与主题而展开探究活动叙事的活动，目的是为了创造优质的教学[2].

根据课程标准（2017年版2020年修订），主题一“预备知识”中涉及的内容有：集合、常用逻辑用语、相等关系与不等关系、从函数观点看一元二次方程和一元二次不等式.人教社A版在處理教材时，构建了两章，即第一章“集合与常用逻辑用语”和第二章“一元二次函数、方程和不等式”，笔者认为这两章之间可以用“集合”的语言将这四块内容串起，加深预备知识的理解，落实主题教学的观念，真正达成初高中数学学习的过渡.

1 重构“预备知识”的思维路径

集合是刻画一类事物的语言和工具，使用集合语言可以简洁、准确地表述数学的研究对象，掌握一门语言最好的途径就是“使用”，因此需要用集合的语言来表达所研究的各种对象，并能以此贯穿整个“预备知识”，重构思维路径.

1.1 集合研究的内在逻辑与外化运用

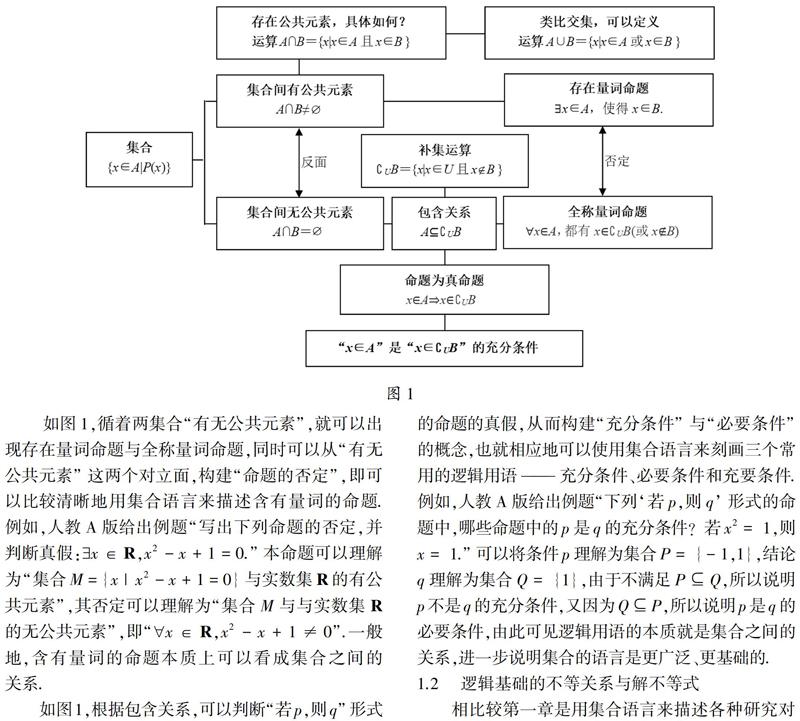
集合的研究方法，主要是“类比”，类比的对象是学生非常熟悉的“数”，遵循数的研究路径：定义—关系—运算，就获得了集合需要研究的内容：关系和运算[3].的确，研究两个集合的关系，可以类比数的大小关系，构建“包含”关系，形成“子集”概念，但笔者认为，从两个集合之间的关系来说，最直白的分类依据是“有无公共元素”.如果有公共元素，那么就需要研究有哪些公共元素，形成“交集”运算，特别地，如果所有公共元素构成的集合恰好是其中某个集合，就可以构建“包含”关系;类比“交集”中用“且”联结，可以用“或”联结来定义“并集”运算.如果没有公共元素，那么发现某个集合包含于另一集合的“对立面”，即形成“补集”运算.至此，对于集合的研究便形成了极其清晰的研究路径，如图1.

教学中问题的设置应该具有一定的目的，本问题主要能够将这两章的内容加以整合，在解决问题中灵活选择，达到复习的目的.虽然问题的形式是第一章的集合关系，但是问题的转化集中展现第二章用函数研究方程、不等式和最值的“统一观念”，也就是德国数学家F·克莱因（F.Klein）所指出的：“我确信函数概念的教学是学校的灵魂，以函数为中心，将全部数学教材集中在它的周围，进行充分的综合.”[7]

“预备知识”应该不仅仅是知识方面对初中与高中的衔接，更应该是思想方面的衔接，特别是学习方法和研究技术的衔接.倘若要让主题教学观念得以落地生根，那就得从“预备知识”开始，让教师刻意引导学生去体会和感悟“主题”，最终实现用“主题”来指导自己的学习，形成“主题学习”的理念，推动“探究学习”的实践，提升学生的数学素养.

参考文献

[1] 史宁中，王尚志.普通高中数学课程标准（2017年版）解读[M].北京：高等教育出版社，2018.5：253.

[2] 钟启泉.学会“单元设计”[N].中国教育报，2015-06-12（009）.

[3] 王嵘.作为语言来学习，发展数学抽象素养和逻辑推理素养——人教A版《普通高中教科书·数学》第一章“集合与常用逻辑用语”介绍[J].中学数学教学参考，2019（25）：12-13.

[4] 宋莉莉.在回顾、梳理基础上提炼、迁移，发展一般性的思想方法——《普通高中教科书·数学（人教A版）》（第一册）第二章“一元二次函数、方程和不等式”的教材设计与教学思考[J].中学数学教学参考，2019（31）：19-22.

[5] 刘洁民.数学文化： 是什么和为什么[J].数学通报，2010，49（11）：11-14.

[6] 刘炜.主题教学引领的“等差数列的前n项和”的课堂实践与反思[J].中学数学月刊，2020（05）：11-14.

[7] COONEY T J，WILSON M R.Teachers′ thinking about functions：historical and research perspectives [M].Hillsdale：Lawrence Erlbuam Association Publishers，1993.

作者简介 刘炜（1983—），男，江苏东台人，中学高级教师，硕士，主要从事中学数学教学与研究.