小学第一学段学生数学多元表征能力的调查研究

□ 李建良 吴小燕 项祖法

在数学学习活动中，数学表征起到了极其重要的作用，数学表征能力发展在很大程度上影响着学生的数学学习水平。一般认为，数学表征是指用一种便于思考和表达的形式来表示数学问题中的信息或对象，从而更好地思考、分析和解决问题。数学表征具有多元形式，包括模型、图形、图像、口头语言、书面语言和形式化的符号语言等。那么，在自然教学条件下，小学第一学段学生的数学多元表征意识与能力的发展会呈现怎样的特征和规律？在学生数学思考与问题解决的过程中，数学多元表征究竟发生了怎样的作用呢？我们对A校2017级110 名学生（各年人数略有变化）进行了为期三年的跟踪调查。

一、调查的目的

具体的目的有两方面：一是关于第一学段学生的数学多元表征水平，即了解学生在数学学习过程中自然形成的多元表征意识与能力处于何种水平，表征方式有怎样的特点，多元表征与问题解决之间是否存在必然的联系等；二是关于数学多元表征的应用和教学，即了解怎样的表征方式有利于问题的解决，教师如何有针对性地在教学中渗透数学多元表征并逐步培养学生的相关意识和能力。

二、调查的时间、内容和形式

连续三年每年进行一次调查，每次调查均以书面测试的形式开展，每次测试均为15个小题，问题以教材内容为基础。为充分反映学生的数学多元表征能力，体现数学多元表征对数学学习的作用，尽可能避免不经表征直接列式计算的情况。15个测试题有不同程度的思维含量，并明确要求学生除了列式解答之外，还要用恰当的方式表示自己的思考过程。

每次测试均分为两轮，首轮为学生自主表征并解决问题，即在测试卷上用自己认为合适的方式对问题信息进行表征以帮助思考与解决问题；次轮为学生根据教师提供的表征方式解决问题，该轮测试题由首轮测试题按照由易到难的顺序重新调整，并辅以不同形式的数学表征，简单的问题辅以单一的表征，复杂的问题辅以多元混合表征。

历年的书面测试均安排在当年的6月份，为保证充分展现学生的思考过程，每次测试时间均为1小时。

三、调查结果及分析

（一）表征形式的总体发展趋势

通过对三年总计332 份调查卷中的4980 个问题结果进行统计，发现第一学段学生比较常用的表征方式有图示、文字、数字、式子（含等式）和表格。各年中这几种表征方式的使用率虽有波动，但总体规律较为一致。总体而言，图示表征约占所有表征方式的45%左右；随后依次是文字表征、数字表征，约各占10%；式子表征和表格表征各占1%左右；其余为无表征（如图1）。三次测试结果表明，画图是学生进行数学表征的第一选择，这与学生的年龄特征以及画图直观形象的特点有关，并且画图这一方式适合对大部分问题进行表征。此外，在对一些特殊问题进行表征时，学生也会选择文字、数字等其他表征方式。

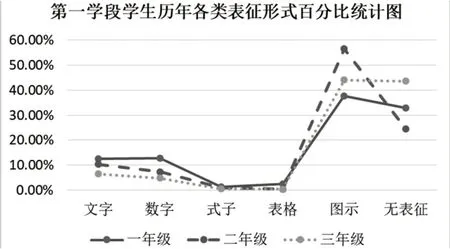
图1

在解决问题的过程中，学生能自发地选择画图这一方式进行表征，这是一个可喜的现象。但如果过度集中于画图这一种方式，将不利于学生理解多种表征方式及其价值，也不利于学生在各种表征之间建立联系，从而影响综合运用多种表征方式分析与解决问题。

（二）表征丰富性的个体发展趋势

通过对历年学生个体表征种类数量的统计，发现在对全部15个问题进行表征时，用到3种表征方式的人数最多；对于同一个问题，大部分学生采用单一的表征方式，较少学生在个别问题中能同时使用两种或两种以上表征相结合的方式（如图2）。

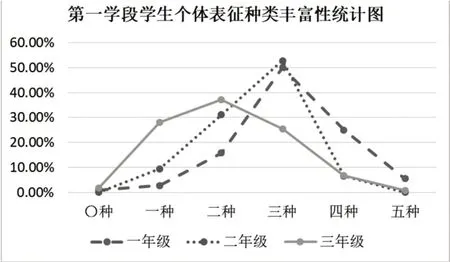
图2

按照一般的规律，难度越大的问题，越需要借助多元表征解读和分析信息，分解问题的难点。但实际情况是在历年的测试中，三年级测试题难度最大，学生表征的愿望和水平反而明显有所下降，且表征的丰富性也受到较大的限制。这说明，在往年的调查中，存在部分学生为了表征而表征的现象，他们的表征仅仅是因为被要求表征，并未将表征与问题解决联系起来，也没有真正理解表征的意义和价值，而一旦遇到真正需要表征时，却不能有效地借助表征描述和分析问题。

（三）表征水平与解答水平的关系

为了研究学生的问题表征水平与解答水平之间是否存在一定的联系，我们通过如下评分标准（如表1）对两者进行赋分，以便进行量化研究。

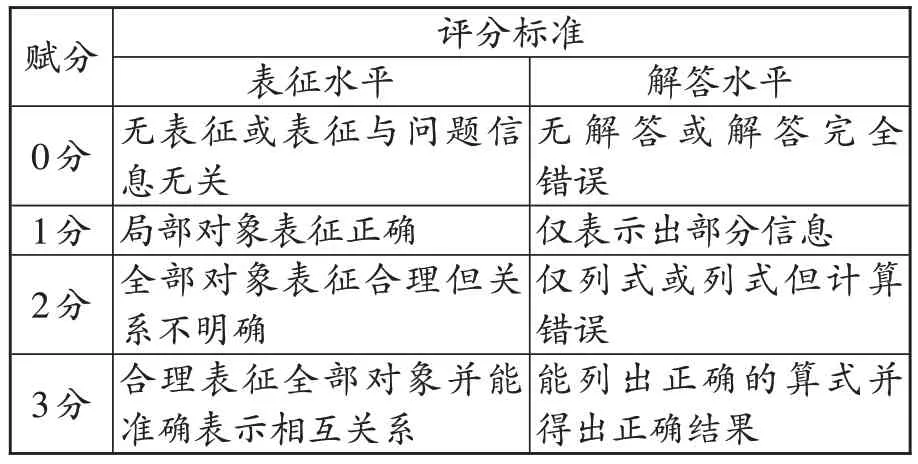
表1 问题表征水平与解答水平评分标准

对历年测试中每个学生的表征水平和解答水平进行赋分，并以0.5分为一段进行人数统计（如图3）。从图中可以发现，表征水平得分在1.5分（即平均水平）以下的有263人次，占总数的72.59%，解答水平得分在1.5 分以下的有220 人次，占总数的66.27%。可见，面对有一定思维含量的测试题，学生整体表征水平和解答水平均不高，两者相差不大，前者略低于后者。

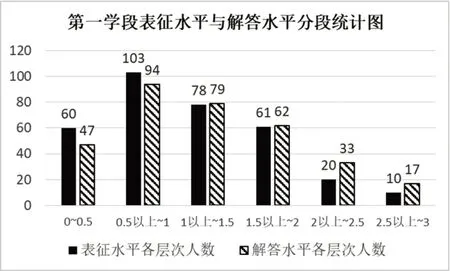
图3

换一个角度，如果计算每一名学生表征水平与解答水平的分差，也将这一分差按照每0.5 分为一段进行统计（如图4）。由图可知，分差在0±0.5 这一范围内的人数最多，合计242 人次，占总数的72.89%，而这一范围意味着表征水平和解答水平差距最小。可见，大部分学生的表征水平和解答水平较为一致。分差为0.5 以上（表征水平明显高于解答水平）有33 人，分差为-0.5 以下（表征水平明显低于解答水平）的有57 人。在两种水平有明显差距的学生中，解答水平高于表征水平的人数更多，从学生的答题情况中也可以看出，部分学生在面对数学问题时，更倾向于不借助表征直接列式解答。可见，在自然教学状态下，通过数学多元表征解决问题并不能成为学生的自发行为。

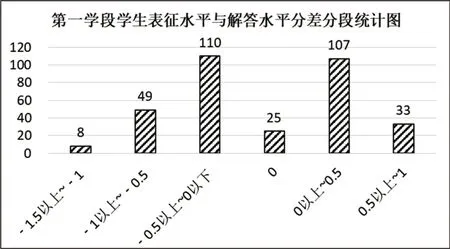
图4

（四）有效表征与问题解决的关系

通过对第一学段学生自主表征整体水平的调查和具体个案的分析，发现学生中存在表征方式选择不合理，表征形式单一，表征与问题信息之间的关系不够紧密等问题。因此，在第二轮测试中，教师为学生提供了适合每个问题的表征方式，并且按照由易到难的顺序，问题的表征形式逐步增多。一般按照表2所示的顺序提供表征方式，难度相似的问题之间表征方式随问题的特点有所调整。

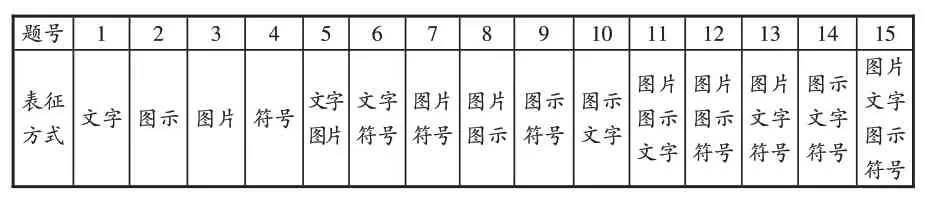
表2 各小题提供的多元表征类型

从上文可知，在自然教学状态下，学生的自主表征能力并没有明显的增长。但从连续三年的调查中发现，总体而言，在教师提供规范、合理的表征方式之后，学生的答题得分基本都有所提升。由图5可知，学生运用教师提供的表征方式解决问题的能力是随着年龄的增长而逐年提升的。尤其是对于难度较大的问题，规范的表征所起到的启发作用越来越明显。历年的测试题中，第11 题至第15 题的难度都比较大，因此教师提供的表征形式也达到了三种或三种以上。对于这些有难度的问题，一年级时，教师提供的表征方式所起的作用并不明显，二年级时，学生在利用这些表征解决难题时的表现不太稳定，到了三年级，规范的表征对解决难题的作用有了明显的提升。

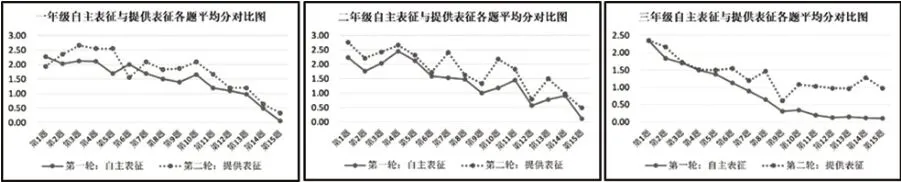
图5

从以上特点可以看出，第一学段的学生已经了解了数学表征的几种基本形式，但他们不善于根据问题信息自己创造表征来帮助思考和解决问题。不过，随着年龄的增长，学生逐渐意识到了数学表征的价值并能尝试运用已有的表征且起到了明显的效果。

四、调查发现与启示

（一）表征的水平不会随年龄增长而自然提升

调查发现，在第一学段中，如果没有人为的干预和渗透，学生的自主表征意识与能力并不会随着年龄的增长而增长。在三年的跟踪调查中，学生在自主表征时主要用到的表征方式并没有明显变化，且有单一化的趋向，即不断偏向于画图这一表征方式。通过对学生表征方式的逐个分析，我们还发现，仅画图而言，也逐渐由画示意图发展为画线段图。画图的本意是发展学生的几何直观，使复杂抽象的问题变得简明直观，但是对于第一学段的学生来说，线段图过于抽象，并且不能解决所有类型的问题。此外，文字、数字、表格等表征形式的占比也逐年下降，表征形式的丰富性受到了极大的限制，这不利于学生发展和形成借助多种表征的共同作用解决问题的能力。

上述现象无疑与教师过于强调思考过程的抽象化有关，由此也看出教师教学对学生发展的影响。如果教师过于强调线段图，学生则自然会选择用线段图进行表征，画不出线段图时只能放弃；反之，如果教师能有意识地渗透多元表征，学生则会尝试运用更多的表征方式以及表征方式的组合来解决问题。这从三年级的调查结果中也可以得到印证，当问题变得复杂时，学生无法运用相对抽象的线段图进行表征，只好选择直接列式或者干脆放弃尝试。

（二）有效的表征能提高学生的问题解决能力

显然，教师的干预对学生表征意识与能力的发展会产生明显的作用，这个作用有可能是积极的，也有可能是消极的。从“每一年第二轮测试时教师为学生提供的表征能促使学生问题解决得分明显上升”这一现象可以得出结论，规范、有效、形式丰富的数学表征，能帮助学生深入思考，发现问题信息之间的联系，从而更好地解决问题。

通过对具体的学生表征和解答的个案分析，我们发现，对于优等生而言，只需要使用书面文字或图示等静态的表征方式，即可解决问题；对于中等生，则需要借助可供操作的学具、教师的口头提示等来解决问题；对于后进生，则需要借助动画演示帮助他们进行思考，部分较复杂的问题，综合运用上述表征方式或者教师加以适当提示，学生也能解决问题。并且，如果将数学多元表征运用到真实的课堂教学活动中，在师生互动、生生互动中，学生能获得更大的启发，多元表征会发挥更大的作用。

（三）教学干预的最终目的是培养学生的自主表征能力

在教学中，教师要积极思考，如何在面对不同的教学内容时，采用最恰当的表征方式，使学生在模仿的过程中，逐步提高数学多元表征的有效性。同时，为了培养学生的自主表征意识与能力，教师为学生提供表征方式时，要注意尺度的把握，不能越俎代庖，以教师的思考替代学生的思考。教师在进行多元表征示范时，提供的表征方式除了包含基本信息之外，不宜过多地呈现其他信息，而应留有余地，这会有利于学生不断地对表征方式进行补充和丰富，有利于学生主动利用这些表征组织并发现信息之间的关联。另外，教学中应采用教师示范与学生自主尝试相结合的方式，通过交互活动提高学生的数学多元表征能力。对于一些特殊的问题，在条件允许的情况下应使学生有机会进行动手操作，对于解决问题过程中的难点应以合理的方式给予学生适当的指导。

在教学中，教师要引导学生通过经历多元表征过程，不断思考、学习如何合理运用表征方式，提高自主表征的能力。在此基础上，还要鼓励学生在多种表征之间进行转换与转译，养成从不同的角度思考问题以及用不同表征相互启发印证的习惯，进而提高学生分析问题与解决问题的能力。