项目化推进：“玩转圆柱”结构化学习的设计与实施

□ 夏萍华

基于学生已有知识和经验基础的结构化学习是当下极具价值的一种学习方式，这种学习方式具有统整性和关联性，是学生对一节课的信息、一个单元的内容、一系列活动间的元素和关系进行整体关联后，主动建构学习的过程。项目化活动是指将数学学习内容与数学游戏、真实性任务等有机整合，以展开系列活动，让学生在活动中主动探究，自主联结已有知识结构去解决新问题，是从学到用的过程。

“玩转圆柱”结构化学习项目（如表1）是在学生学习了“圆柱与圆锥”单元后，教师统整了本单元核心概念及学生学习中的困惑与不足，对相关学习材料和内容进行适切的开发形成的，旨在通过项目化学习活动引导学生将学习经验自主迁移到“新情境、新问题”的探究解决过程中，实现从“学结构”到“用结构”的过程。该过程既可完善原有的认知，又打通和发展数学的方法结构、思维结构以及策略结构，效果明显。

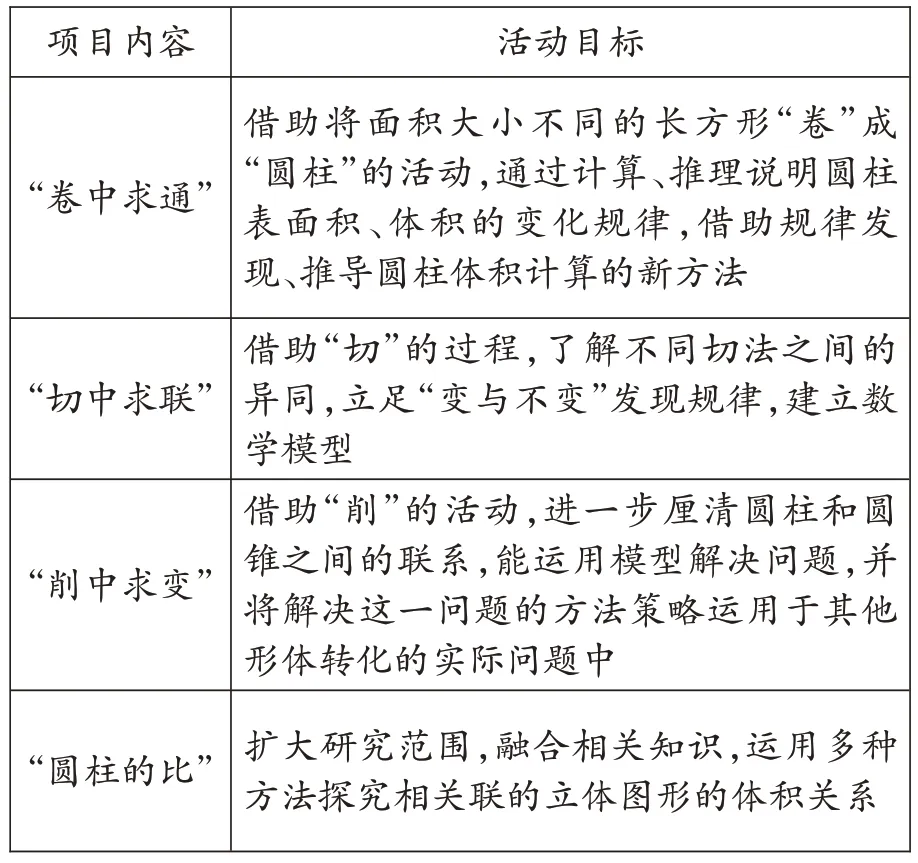
表1 “玩转圆柱”结构化项目活动的整体框架

“玩转圆柱”结构化学习以4个项目推进，借助结构化的学习材料，让学生在“真实活动”中经历操作探究，通过类比辨析，感悟数学结构学习的魅力。

一、“卷中求通”项目：增补内容完善知识结构

数学知识在教材中以一定的结构分布排列，各知识间既有个性又有共性，紧抓素材背后的共性知识进行探究，可达到知识结构和认知结构的同生共长。“卷中求通”项目借助结构性材料“面积是36cm2的长方形”，从“卷”圆柱活动展开。

（一）利用结构材料，联通基础知识

提问：用这张长方形纸卷成一个圆柱体的形状，你能获得圆柱的哪些信息？

活动要求：四人小组合作，卷一卷，画一画，并记录。比比谁获得的信息更丰富。

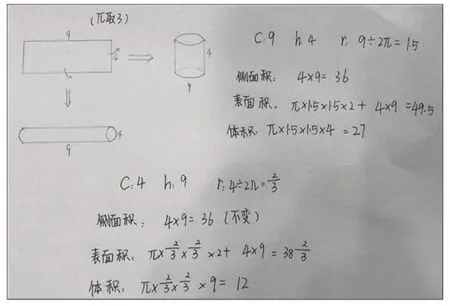
图1 “卷中求通”项目学生作品1

从图1中可以看出，学生在基础活动中能自主勾连本单元中的重要概念，可见学生对本单元的基本知识结构已经初步形成，并积累了较丰富的活动经验。

（二）通过验证推理，弥补知识断层

在唤醒学生已有的认知结构后，教师用结构化材料“面积是36cm2的长方形”和问题串“小组合作，试试能卷出哪些不同的圆柱？这些圆柱之间有什么异同”，引导学生有序思考、分类研究。

在任务驱动下，学生活动的过程展开充分，生成的资源丰富多元。

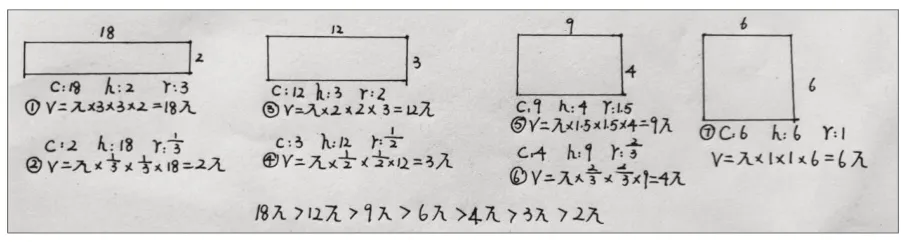
图2 “卷中求通”项目学生作品2

从图2的呈现可以看出，学生已经有了很强的结构化学习能力，展现出了有序思考的习惯，体现出较高的思维水平。教师借助生成的结构性材料继续进行如下操作。

提问：再观察，你又有什么发现？

发现：S侧一样，沿长边卷，表面积越大，体积也越大。

设疑：明明是面积的研究，怎么体积也会有这样的规律？

解疑：再研究圆柱体积的推导过程（课件动态演示，如图3）。

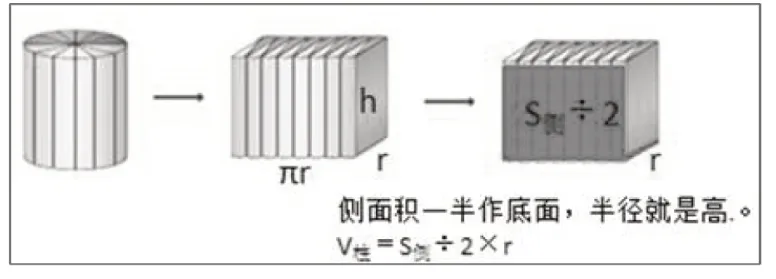
图3 圆柱体积推导过程再研究课件

在课件的直观演示下，切拼成的长方体形象在学生的脑海中动了起来。通过想象旋转的过程，学生进一步理解体积概念的本质，化解了特定思维的干扰，通过探究可以得到求解圆柱体积的新策略。

（三）借助习题拓展，完善知识架构

通过“卷”的过程，学生联通了S侧、r、V 之间的关系。一种新策略出现后，需要跟进练习，在应用中进一步巩固理解。

题组1（原高频错题）：

①用面积是36cm2的长方形“卷”一个底面半径是2cm的圆柱，这个圆柱的体积是多少？

②如果一个圆柱的侧面积是200cm2，底面半径是2cm，那么这个圆柱的体积是多少？

此时学生再做这两题，都直呼“简单！”可见在“卷中求通”项目中，学生实现了对原有知识结构的一次充盈，完善了自我的认知结构。

二、“切中求联”项目：多元变式打通思维结构

学生学习基本知识一定要求联，在联系中感受知识关联、结构关联、思想关联、方法关联。“切中求联”项目在同一圆柱“多样切法”活动中推进。

（一）通过知识联结，盘活思维力度

稳固的知识结构是充分调动学生思维张力的保障。“切中求联”项目借助结构化问题“看信息写算式想生活问题”（如图4），促进学生思维的发展。

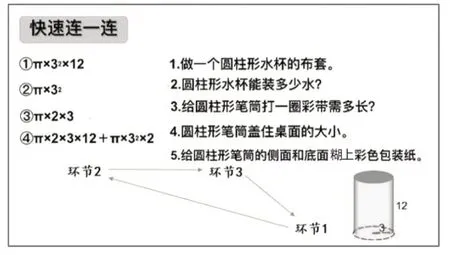
图4 “切中求联”项目导入环节课件

（二）巧在切中求变，拓展思维宽度

围绕核心问题“如果切一刀，会有哪些不同的结论？如果切不止一刀呢”开展探究活动，学生的兴趣被充分激发。图5 是学生在项目活动中的部分成果，从中可以看出学生在动手操作、合作探究中思维得到了进一步拓宽。

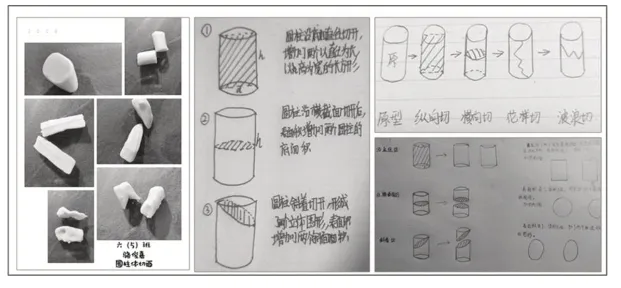
图5 “切中求联”项目学生课后拓展作业作品

借助直观操作，学生全面思考了有哪些不同的切法，并在对比中发现，无论怎样切，圆柱体都是“体积不变，表面积增加，不同切法增加的表面积不同”。这样的“协变思维”打通了学生已有的数学思维结构。

（三）加强对比辨析，挖掘思维深度

如何继续挖掘思维深度？下面的对比辨析是不错的选择。

题组2：

①一个高12cm 的圆柱，将它截成2个小圆柱，表面积增加了50.24 cm2，这个圆柱原来的体积是多少？

②一个高12cm 的圆柱，如果截掉一个2cm 高的小圆柱，表面积减少了50.24 cm2，这个圆柱原来的体积是多少？

通过找一找、说一说、画一画等直观表征，学生明确了两个“50.24”意义上的区别，并根据区别进入程序性解决问题环节。“切中求联”项目引导学生在“变与不变”的本质探究中发现规律，并形成了一定的思维模型结构。

三、“削中求变”项目：协变思维盘活方法策略

好的活动教学力求设计求变，方法求变。变玩法、变信息、变模型、变图形、变思路等，在变中发现不变，感悟知识结构和方法结构的不变。“削中求变”项目借助模型探究圆柱与圆锥的关系，并在此基础上将“削”圆柱活动推广至其他立体图形。

（一）结合摸底谈话，探明变式方向

前面的活动结束后，教师追问：“玩转圆柱，还能怎么玩？可以将圆柱削成哪些不一样的图形？”这样的开放性问题点燃了学生的兴趣，在谈话中可以发现，学生在前面的项目活动中积累的经验得到了良性迁移，提出可以变玩法、变图形、变思路等等，教师由此摸清了学生的能力起点。

（二）结合模型建构，追寻变与不变

模型思想是数学的重要思想。圆柱与圆锥S底、h、V三者关系的辨析对于大部分学生而言存在障碍（见题组3），图6 中的三组模型是解决这类问题的“脚手架”。通过“想象模型—复原模型—模型辨析”，学生明确了每组模型中的“变与不变”，并渐渐在脑海中形成模型结构。

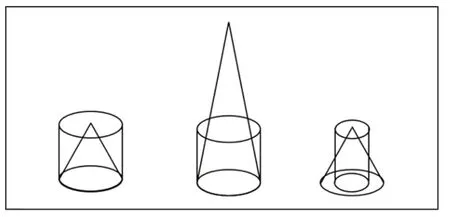
图6 “圆柱与圆锥”相关联的三组模型图

题组3：

①一个圆柱的底面直径是4，高是6，与它等底等高的圆锥的体积是（）π。

②一个圆柱和一个圆锥体积和底面积都相等，圆柱的高是15，圆锥的高是圆柱高的（）。

③一个圆柱和一个圆锥的体积相等，高也相等。圆柱和圆锥底面积的比是（）。

（三）促进活学活用，勤思方法拓展

课后挑战性作业“将圆柱削成最大的长方体，你能提出哪些有价值的问题”是“削中求变”项目的点睛之笔。在学生自主研究的过程中，教师发现活动中的模型思想、方法策略结构，学生都能够迁移运用，并能借助直观图示尝试在三维立体图形和二维平面图形间建立勾连。

四、“圆柱的比”项目：认知迭代展望能力结构

数学是思维的体操。在数学学习过程中，有些知识会随着时间的流逝被逐渐忘却，但数学思想和方法却不会被忘却。“圆柱的比”项目紧扣“套娃模型”，在“看图想物”活动中展开。

（一）借套娃模型，引知识发声

教师出示图7，并提问：图中是小学阶段所学的四种立体图形，这组图形让你想到了哪种物品？

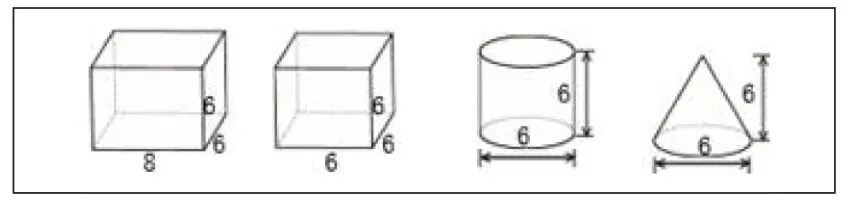
图7 “圆柱的比”套娃图

“套娃”模型素材来源于教材，是“圆柱的比”项目中的核心素材，挖掘其背后的功能，调动学生的知识联结，可以为多角度研究“比”奠定活动基础。

（二）多角度对比，展认知迭代

用数学眼光看问题，用数学方法解决问题，是数学能力素养在数学学习过程中进行不断迭代的最好呈现。多元策略解决问题，既能考查学生知识结构的范围，也能展现学生思维水平的层次。“你会怎样比较它们的体积？”学生依次想到了“计算体积、等高比底面积、等底面积比高、用大套小”等不同的方法。知识不断地输出、迁移、迭代，提出新策略的过程，就是知识内化、方法优化的过程，学生的能力结构在逐渐形成。

（三）再拓展探究，拓能力素养

好活动一定能往下继续延伸，探究性练习能让学生的思维保持活跃。

题组4：

①长方体与正方体的体积比是（）。长方体的体积比正方体大（）%。

②圆柱的体积占正方体体积的（ ）%。

“圆柱的比”引导学生对不同立体图形进行关联性研究，唤醒学生联结更多的知识，用知识、用方法、用思想，让数学学习的思维和能力向更高层次进阶。

“玩转圆柱”四个项目的结构化学习，让学生经历了基于原有认知的结构化项目探究过程，从“学结构”到“用结构”。学生的数学学习方法、思维结构、策略意识都在学习过程中迁移发展，学生数学能力、知识素养都在这一过程中不断提升。