单井增强型地热系统性能分析
蒋坤卿,黄思浩,李华山,卜宪标
(1中国科学院广州能源研究所,广东广州510640;2中国科学院可再生能源重点实验室,广东广州510640;3广东省新能源和可再生能源研究开发与应用重点实验室,广东广州510640;4中国科学院大学,北京100049)
地热能作为一种新能源形式,与传统化石能源相比,性能稳定,可以连续性生产,对环境影响小,其开发过程不受气象条件影响[1-2]。尽管地热能有足够多的优势,但其目前的开发利用却并不顺利,传统的水热型地热能利用要求地下热储具有足够的温度和水量并且要易于采灌,而满足这些条件的热储并不多见[3-4]。具有广阔前景的EGS系统目前也面临着技术和经济问题[5-6]。近年来,一种新型的深井换热器(deep borehole heat exchanger,DBHE)因为不受地热热储的限制且没有回灌问题,逐渐引起人们的关注。
DBHE整体采用全封闭的同轴套管结构,可以采用水或者其他的工作流体进行换热。实际建设过程中将废弃油气井改造成DBHE可以省去钻孔过程,减少建设的初投资[7-8]。Morita等[9]针对DBHE进行了试验测试,在测试过程中得到的最大净热输出为370kW,最大出口温度为98℃。Bu等[10]指出间歇式的运行方式可以缩短DBHE的投资回收周期。Song等[11]指出内管的保温性能对DBHE的影响较大,而且在保温效果与成本方面存在一个最佳的保温长度。Deng等[12-13]对DBHE进行了现场测试以及仿真,研究了单井供暖系统中热泵与供水系统的优化问题并分析了DBHE的传热性能。Liu等[14]分析了层状的地下结构对DBHE换热性能的影响。Luo等[15]利用分段有限柱热源模型对DBHE进行了分析。Pan等[16]对影响DBHE换热的因素进行了敏感性分析,指出外管直径、井深以及流量对其热提取率影响最大。除此之外,还有部分研究者分析了DBHE在地热发电方面的应用表现及其影响因素[17-23]。
虽然DBHE在地热能利用方面有其特有的优势,但是它的单井换热量不高,限制其应用推广[24]。为了强化单井的换热能力,部分研究者在DBHE的基础上提出了新式的单井地热换热器[25-29]。Wang等[25]提出在DBHE底部外套管附近修建第二环空,在第二环空的外围建立人造热储,水作为二次循环流体以自然对流的方式将热量带至外管附近。Huang等[26]将热管与人造热储相结合,以二氧化碳为二次循环流体从人造热储中取热。Dai等[27]提出一种具有开式结构的DBHE,使单井可以与地下含水层之间进行对流换热。Cheng等[28]尝试在DBHE下方建立人造热储以强化单井的换热能力。Feng等[29]提出可以在含水层布置泵来驱动热储层的地热水与DBHE之间进行对流换热。
受到以上研究者的启发,本文提出了一种新型的单井增强型地系统(single-well enhanced geothermal system,SEGS)。通过在地热单井的周围建立人造热储引入对流换热,用以强化地热单井的换热效果。地热井在人造热储附近采用开式结构,使单井中的工作流体可以进入热储换热,这样既可以强化单井的换热能力,也不用担心传统的EGS系统所具有的难以在生产井与注入井之间建立水力连接的问题[30],而且由于整个换热过程不强制换热流体进出热储,循环泵功也相对较小。此外,因为仅仅在钻孔周围附近建设人造热储,所需的费用比双井EGS系统低,如果将合适的废弃油气井改造成SEGS,还可以进一步减少建设的初投资。本文建立了SEGS的二维数值模型,并利用数值模拟的方式分析了利用SEGS系统进行地热能开采的可行性,并对各种可能影响系统换热能力的因素进行了研究。
1 单井增强型地热系统
1.1 SEGS的基本原理
本文提出的单井EGS模型结构如图1所示,其基本结构和DBHE相似,只不过在同轴换热器的周围建立了人造热储,同轴换热器在热储附近使用开式结构,当换热流体从内管或者环空注入时,可以通过外管的开孔段进入热储参与换热。换热流体可以以对流的方式将热储的热量带至地热井中,同时在非开孔段,岩石中的热量也可以以导热的方式传递至同轴换热器的外管。
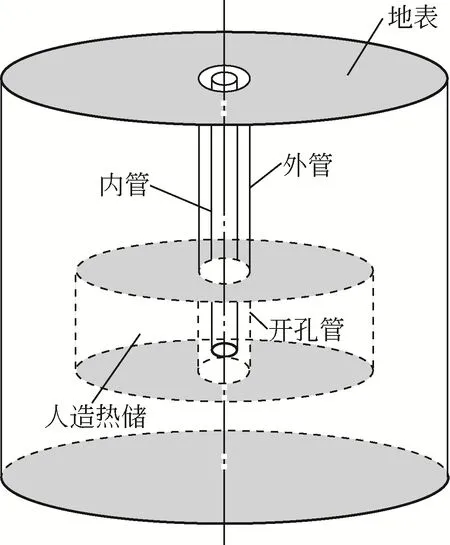
图1 SEGS结构
1.2 数值模型
(1)模型假设
本文在模拟过程中将人造热储等效为均匀且各向同性的饱和多孔介质,同时认为地下岩层的物性也是均匀且各向同性的。换热流体为水,在本文中水的热物性除黏度外认为保持恒定。本文考虑了水在驱动压头以及浮升力的共同作用下在热储区域的流动以及换热过程,换热过程中所涉及的自然对流现象由Boussinesq假设进行描述。水的黏度随温度的变化以式(1)给出[31]。

(2)连续性方程[式(2)]

式中,ρ为流体的密度;v为速度矢量。
(3)动量守恒方程
流体的动量守恒方程如式(3)。


对于多孔介质区域的动量方程,可以通过在式(3)的基础上加入基于达西定律的动量源项的方式实现,动量源项形式如式(4)所示。

式中,α为多孔介质的渗透率;μ为流体的黏度。
(4)能量方程[式(5)]
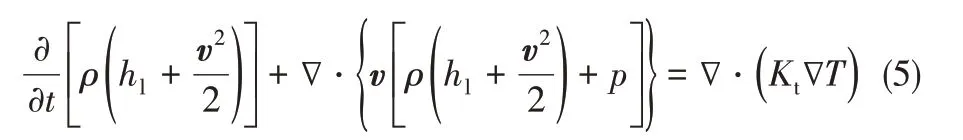
式中,hl为液体比焓;Kt为液体热导率。
在固体区域能量方程形式如式(6)所示。
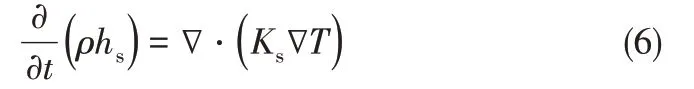
式中,hs为固体比焓;Ks为固体热导率。
式(5)和式(6)中,比焓的表达如式(7)所示。

式中,cp为相应介质的比热容;Tref为参考温度。
换热流体是以自然对流的方式在热储中流通,流速较低的流体与岩石之间有充分的时间进行换热,认为在传热过程中多孔介质固相以及液相的温度保持一致,即本文采用热平衡假设模型描述多孔介质中的换热过程,此热平衡模型[式(8)、式(9)]在法国Soultz地区的EGS项目中也是适用的[32]。

式中,hl为流体比焓;hs为固体比焓;ρl为液体密度;ρs为固体密度;Kl为液体热导率;Ks为固体热导率;Keff为多孔介质等效热导率;ε为孔隙率。
2 模型验证
本文对于岩层区域和人造热储区域的换热过程分开进行验证。岩层区域采用纯导热模型,人造热储区域采用多孔介质模型。导热模型和多孔介质模型分别与卜宪标等[33]和Li等[34]的试验结果进行对比。卜宪标等[33]对青岛的一个DBHE进行了供暖试验测试,试验井全长2605m,内管尺寸φ110mm×10mm,试验井更多详细参数请参考原文。试验入口温度约为5℃,体积流量约为30m3/h。其试验结果和本文模型的模拟结果如图2所示。结果表明本文模型的仿真数据与试验结果吻合较好。
Li等[34]对开式结构的地热同轴换热器进行了砂箱试验,其试验砂箱如图3所示,砂箱填充了粒径为2.5~3mm的玻璃珠以及具有一定温度的热水。同轴换热器的内管外径为9mm,开孔管的内径为30mm。入口水温为25℃,入口流量约为40mL/s,砂箱孔隙率为0.4。取玻璃珠的平均粒径为2.75mm,利用Kozeny-Carman方程[35]计算得到砂箱内饱和多孔介质的渗透率为7.68×10-9m2。试验结果与本文模型计算的结果绘制在了图4中,砂箱的初始温度分别为68℃、60℃和50℃。可以看到模拟结果与试验结果吻合情况良好,说明了多孔介质模型的准确性。
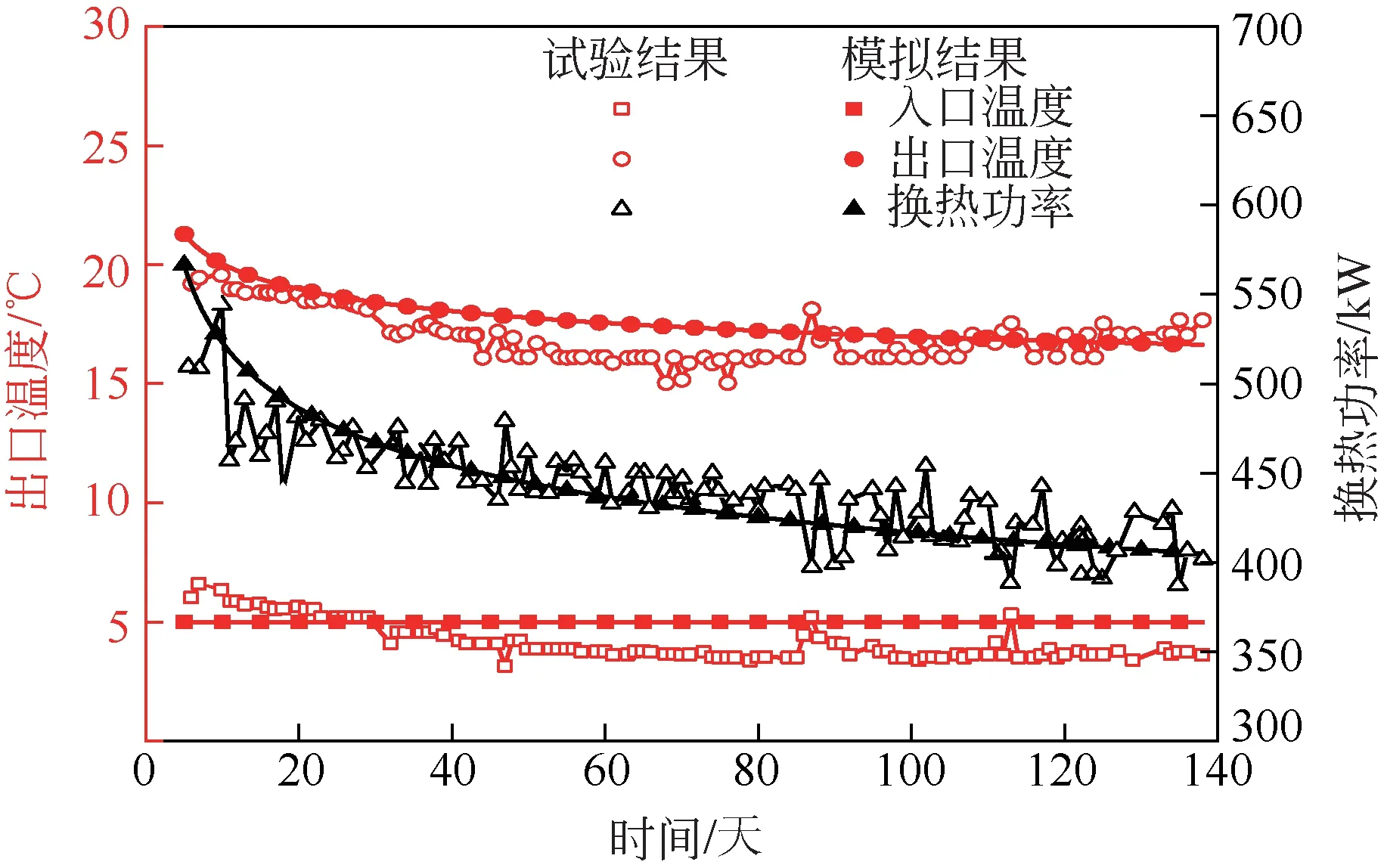
图2 导热模型模拟结果与试验结果对比

图3 试验砂箱
3 模型参数

图4 多孔介质模型模拟与试验结果对比
建立SEGS的二维数值模型并对其换热过程进行模拟。为了描述方便将计算域尺寸绘制在了图5中。图5中H1为换热器导热段的长度,H2为换热器开孔段的长度同时也是人造热储的厚度,H3为热储底部岩层的厚度,R1为人造热储的半径,R2为整个模型的半径。模型导热段的长度为2600m,人造热储的厚度H2和半径R1分别为400m和50m,模型的半径R2=R1+50m,H3固定为80m。同轴换热器的外管尺寸为φ244.5mm×8.94mm,内管尺寸为φ170mm×10mm,换热器外管与钻孔之间用水泥进行填充,固井水泥层的厚度为19mm。参考相关文献[32,36]中的参数设置,热储层的孔隙度设置为0.01,渗透率设置为1×10-12m2。地表的初始温度为15℃,地温梯度为30℃/km。模拟中涉及的其他相关物性列于表1中。模拟采用恒定的入口质量流量以及入口温度,入口质量流量为10kg/s,入口水温为5℃。

图5 计算域

表1 物性参数
用于离散整个计算域的结构网格数量为308334,其中在井内、近井区域以及热储区域进行了网格细化,网格质量良好,为了保证计算结果不受网格划分数量的影响,需要进行网格无关性验证,为此对几个具有不同网格数量的SEGS模型进行了数值模拟,并取第240小时的计算结果进行了对比,所得计算结果列于表2中。从表2中可以看到当网格数量少于231634时,SEGS的出口温度随网格数量有所波动,当网格数量大于231634时,SEGS出口水温已经相对稳定,因此本文模拟所用计算网格数量为308334是合理的。
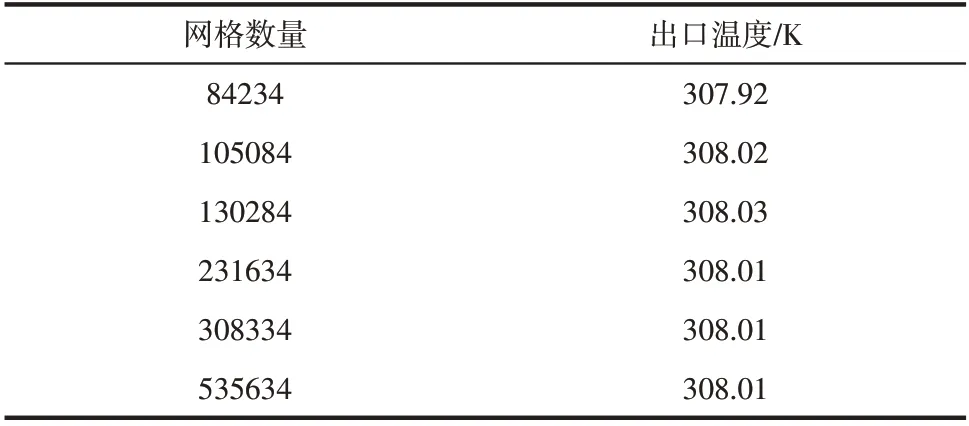
表2 网格无关性验证结果
4 结果与讨论
如前所述,SEGS的换热过程复杂,影响其换热的因素较多。本节将具体分析SEGS的短期和长期运行特性,并对可能影响其换热性能的因素如入口条件、固井水泥保温性能、热储层的结构参数以及单井的结构参数等进行分析。本文主要研究SEGS在建筑供暖方面的应用,供暖期取120天,供暖期结束之后到下一个供暖期之间为恢复期。
4.1 SEGS的短期性能表现
图6所示为SEGS以及DBHE在单个供暖季的功率对比情况。在DBHE的相关研究中,有研究者指出流体从环空注入由内管采出的运行方式有利于换热器的换热[37-38],而SEGS由于存在人造热储中的对流换热过程,其运行特性可能存在不同,因此模拟之初对SEGS两种不同的流体流向都进行了模拟。现规定流体从环空注入,从内管采出的流动方向为正流,反之为逆流。从图6中可以看到,无论SEGS按照哪种流向进行设置,其在单个供暖季的换热功率始终比DBHE高,采用逆流形式的SEGS换热功率明显高于采用正流动形式的SEGS,正流运行模式的SEGS以及DBHE在运行过程中换热功率都有所下降,其中DBHE的功率下降比较明显;逆流形式的SEGS单井换热功率在整个供暖期间都比较平稳,甚至在运行之初还略有上升。逆流模式的SEGS、正流模式的SEGS和DBHE第1个供暖季的平均换热功率分别为1603.6kW、1204.6kW和726.4kW,平均出口水温分别为43.3℃、33.8℃和22.4℃。以上分析表明,SEGS的换热功率较DBHE有明显的提升,尤其是逆流形式的SEGS,其单井的换热功率是DBHE的2.2倍。
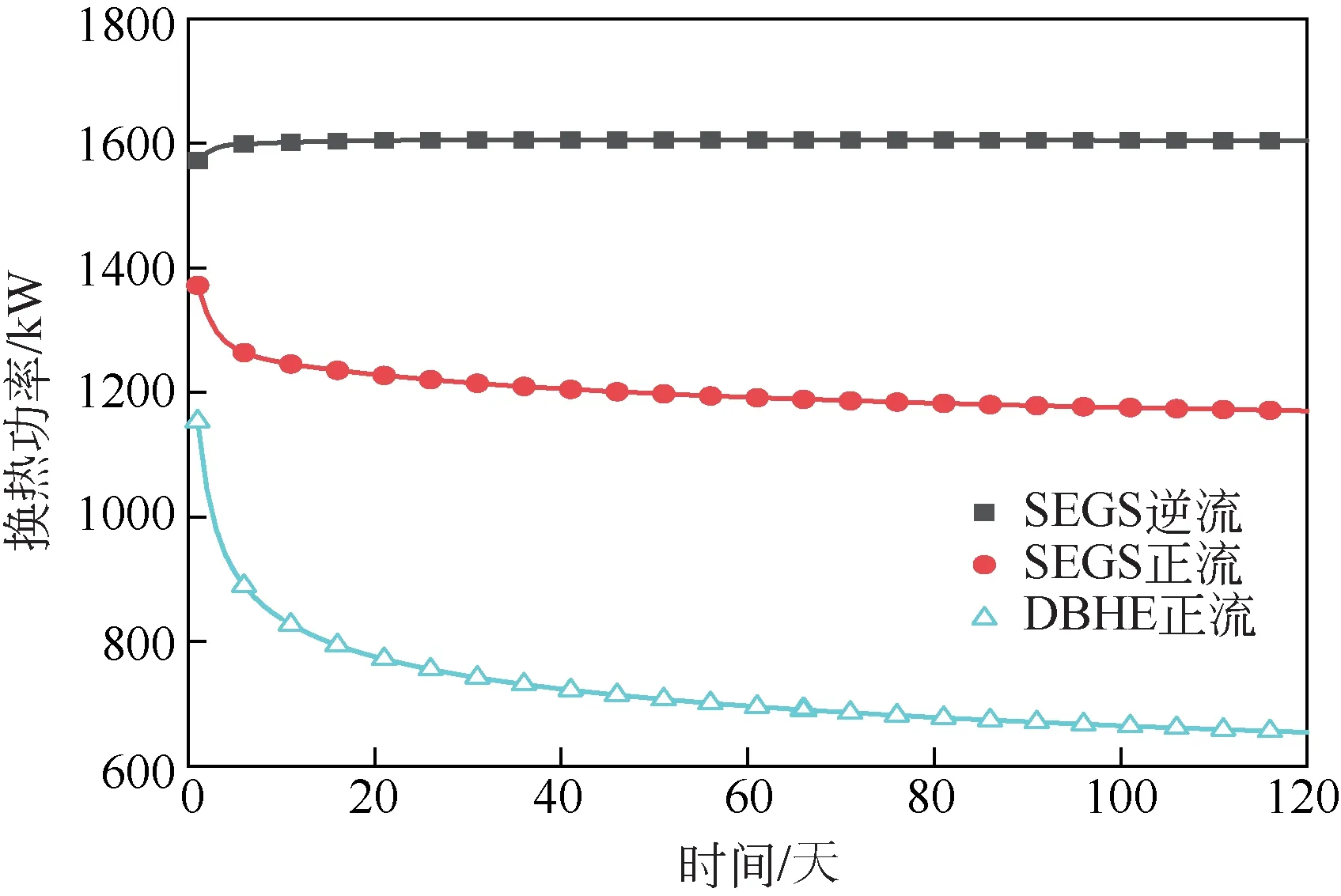
图6 SEGS和DBHE第一个供暖季换热功率随时间变化
SEGS良好的性能表现源于其在单井的换热过程中引入了对流换热的形式,对流换热可将距单井较远处的热量提取出来。图7所示为供暖季末采用两种不同流向形式的SEGS人造热储温度场变化情况,其中r值为距离单井轴心的距离,横坐标ΔT为人造热储初始温度场与第一供暖季结束后温度场的差值,人造热储的顶部深度为2600m,底部深度为3000m。从图中可以看到,两种运行模式的SEGS对储层的热影响都集中在储层底部,即SEGS的取热范围集中于储层底部,这与Cao等[39]的EGS模拟结果类似。在相同位置逆流形式的SEGS换热带来的储层温度变化更大,说明逆流形式的SEGS对热储层的热影响比正流形式的SEGS要更强一些。随着距井轴心半径的增大,SEGS对储层温度的影响越来越小,在半径r=25m处,正流形式SEGS运行所带来的储层温度变化已经难以看出,而逆流形式的SEGS在此处还略有影响,这意味着逆向形式的SEGS热影响范围也比正流模式的大。由上述分析可以看出,逆流的流动形式更有助于SEGS人造热储层对流换热的进行。

图7 不同流向下供暖季末人造热储温度场变化情况
4.2 SEGS的长期性能表现
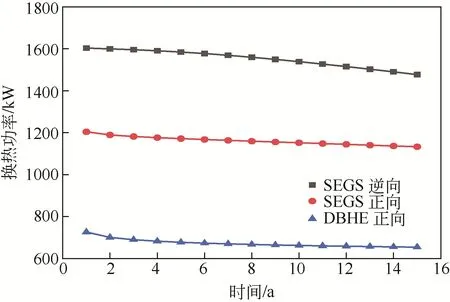
图8 两种地热井平均换热功率随时间的变化
图8所示为SEGS和DBHE各供暖季平均换热功率随时间的变化。整体上DBHE和SEGS的平均换热功率都在随时间下降,其中正流形式的SEGS和DBHE功率下降速度相对均匀,而逆流形式的SEGS在第4个供暖季开始功率下降变得比较明显,但是换热功率依然要比正流形式的SEGS高。图9所示为逆流形式的SEGS在第4个供暖季结束热储层的温度变化情况,可以看到在距换热器轴心50m处热储层的温度已经开始变化,而人造热储的半径同样是50m,这说明第4个供暖季末逆流形式的SEGS的热影响范围已经到达人造热储的边缘,这也是逆流形式SEGS在第4个供暖季之后换热功率开始下降的原因。从图8中还可以看到,即使长期运行之后SEGS的换热功率有所下降,其依然能保持较高的换热功率。在第15个供暖季逆流形式的SEGS平均单井换热功率为1477.2kW,正流形式的SEGS平 均 功 率 为1133.1kW,而DBHE仅 为654.2kW。可见长期运行模式下SEGS的换热能力也能得到保证。
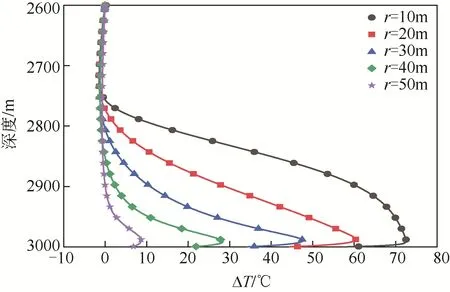
图9 逆流形式SEGS第4供暖季末热储温度场变化
综合以上分析,SEGS无论是在单个供暖季期间还是数个供暖季,其换热能力都比DBHE要好,而逆流形式的SEGS性能要好于正流形式的,因此建议对SEGS采用逆流的运行方式。接下来的所有分析都只针对逆流形式的SEGS展开。
4.3 固井水泥导热性对SEGS的影响

图10 第一供暖季末距井轴心0.5m处岩层温度变化情况
图10所示为第一个供暖季结束后距井轴心半径0.5m处岩层的温度变化情况,其中横坐标ΔT为岩层温度与初始地温的差值,纵坐标为深度。从图中可以看到当深度大于1500m时,岩层的温度相较于原始地温有所降低,井深越大处温度降低越厉害;当井深小于1500m时,岩层的温度相较于初始地温有所升高,井深越小处温升越高,地表处的温升已经达到了16℃。当井深大于1500m时,岩层的温度高于环空中的水温,水流动时在岩层中吸热使岩层的温度降低;而当井深小于1500m时,环空中的水温已经高于岩层的温度,此时水的热量会散失到岩层中,造成热量的浪费。
因此,需要在井深较小处考虑对外管进行保温。设置井深小于1500m处的固井水泥热导率分别为0.1W/(m·K)和0.01W/(m·K)重新开始计算,计算结果绘制在了图11之中。从图中可以很明显地看到,对外管采取保温措施之后单井的换热功率得到了提升,当水泥热导率为0.1W/(m·K)和0.01W/(m·K)时,相应的单井平均换热功率分别为1664.9kW和1713.4kW,与热导率为0.8W/(m·K)相比,换热功率分别提升了61.3kW和109.5kW。此外,对外管进行保温操作前后,SEGS的出口水温随时间的变化趋势发生了改变,而当固井水泥的热导率下降之后,单井在运行之初的功率变化情况由随时间上升变成了随时间下降。这是因为之前单井外侧固井水泥的热导率大,在运行之初换热器中的热量容易散失到地层中,导致单井功率在一开始就较低;随着单井的运行,近井周围的岩石由于被加热而温度升高,致使单井向岩石的热量散失变得困难,单井的功率开始上升。而水泥的热导率下降之后,SEGS向地温岩石的散热变得缓慢,便出现了单井功率下降的变化趋势。
4.4 热储厚度对SEGS的影响

图11 不同固井水泥热导率下SEGS的换热功率随时间的变化
默认条件下人造热储的厚度为400m,在保证热储半径以及单井深度不变的情况下,针对人造热储厚度分别为100m、200m、300m、500m、600m和700m的SEGS进行了模拟,所得结果绘制在图12之中,其中Δh表示热储厚度。从图中可以看到单井的平均换热功率和出口温度在开始时随着储层厚度的增加而增加,之后增长速度逐渐减小,最后还略有下降。这说明储层的厚度对SEGS的换热性能有很大的影响。当储层的厚度为100m时,单井的换热功率仅为900.2kW,储层厚度为300m时已经达到了1502.7kW。储层的厚度增大,单井周围对流换热的区域也就增大了,所以刚开始SEGS的换热性能也随之增大。但是当储层厚度超过一定限度时,储层上方温度相对较低的区域参与对流换热反而不利于单井换热性能的提升。因此,在建设SEGS时并不是热储厚度越厚越有利,而是需要综合考虑地温梯度、井深以及建设费用等因素以求单井的效益最大化,在本文默认条件下储层厚度为400m时已经有足够的换热功率。
4.5 热储半径对SEGS的影响

图12 不同热储厚度下SEGS的平均换热功率和出口水温

图13 不同热储半径的SEGS出口水温随时间的变化
图13所示为不同热储半径条件下单井出口水温随时间的变化。可以看到,SEGS的出口水温总体上随着热储半径的增大而逐渐增大,当热储半径小于60m时,出口水温随半径的变化比较剧烈,当热储半径大于60m时,出口水温随半径的变化比较小。图14为SEGS在单个供暖季平均换热功率随热储半径的变化情况,从此图可以看出单井的换热功率随热储半径的提升而提升,而且这种提升程度是逐渐降低的。热储半径由50m提升至90m,半径每增加10m带来的换热功率提升分别为102.7kW、67.0kW、43.8kW和29.2kW。由此可见,热储的径向尺度对SEGS的换热性能影响同样不可忽视,但是也不应盲目扩大热储的半径,由此带来的成本增加可能得不偿失。结合上一节对热储厚度的分析,在建设SEGS时需要综合考虑厚度和径向尺寸对其换热的影响,寻找最优的热储尺寸组合才能最大限度地发挥单井的换热潜力。

图14 SEGS平均换热功率随热储半径的变化
4.6 入口流量对SEGS的影响
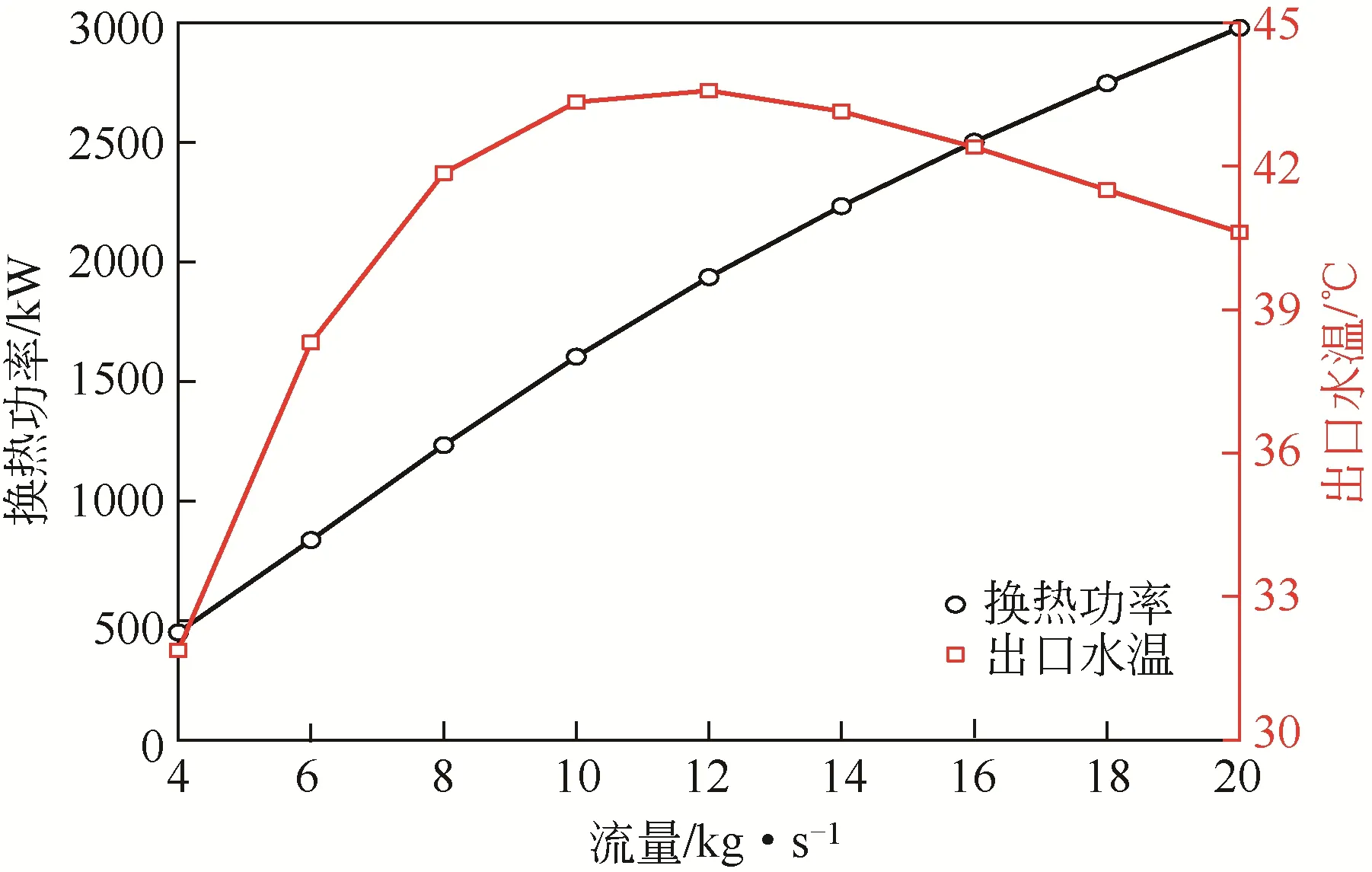
图15 不同进口流量下SEGS的平均换热功率和出口温度
图15所示为不同进口流量下SEGS的平均换热功率和出口水温。SEGS的换热功率与入口流量呈正相关的关系,入流流量越大换热功率越大。而出口水温一开始随流量的增加呈上升的趋势,当入口流量超过12kg/s时,出口水温开始随入口流量的增加而下降。这种现象是多种因素造成的,当入口流量较小时,管内水的流速较低,内外管之间的流体有充分的时间进行换热,导致外管水温降低内管水温增高;同时,当流体从内管进入外管时已经具备一定的高温,使得外管流体与岩层以及热储的温差过小,进而影响了热储区域的自然对流过程以及非热储区域的换热过程。此外,较小的流速也使得井底流体的驱动压头变小,不利于换热流体进入热储区域进行换热。
图16所示为供暖季末内管底部出口的水温随流量的变化。入口流量越小,内管出口水温越高,当流量为4kg/s时,内管出口水温超过了57℃,这样的高温流体进入环空显然不利于单井换热。因此,当流量较小时,随着入口流量的增大,单井的换热性能逐渐增大,SEGS呈现出口水温随流量增大的特征;当流量增大到一定程度之后,虽然单井的换热功率还在增加,但是单位时间内由于参与换热的流体量也在增加,所增加的换热量不足以将单位质量的流体温度升至足够的温度,导致出口水温下降。所以,在实际运行SEGS时,对于入口流量的选择应该慎重,过低的入口流量不利于SEGS的换热。

图16 内管平均出口温度随入口流量的变化
除了分析出口水温以及换热功率之外,本节增加对SEGS地下换热器的增量的分析,以确定入口流量改变时地热换热器的增量变化情况,为整个地热供暖系统的设计与优化提供依据。循环水经由循环水泵到地下换热器再返回地面的过程中,系统获得的增量ΔE由两部分组成,包括流体工质焓的增量和水泵输入压力功增量,而开口稳流系统中流体工质的焓又可分为热量和机械两部分;为了使理论分析具有一般性,可以假设循环水泵使流体压力的增加量恰好等于由于克服换热器的流动阻力所消耗的,最终地热换热器在换热过程中所得到的的净增量ΔE如式(10)所示[40]。
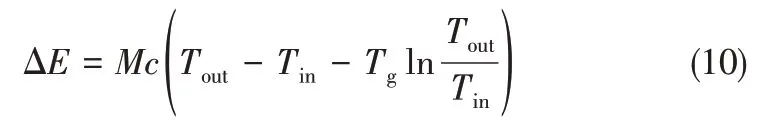
式中,M为换热流体的质量流量;c为水的比热容;Tout为出口水温;Tin为入口水温;Tg为参考温度,接下来的计算Tg均取值278.15K。
图17所示为在不同进口流量条件下SEGS在单个供暖季的平均增量,可以看到随着入口流量的增加,SEGS所获得的增量逐渐增大,当流量大于12kg/s时,增量增长速度开始变缓。这说明较大的入口流量对于SEGS的换热有利,这个结论与前面相同。但是当入口流量增大到一定程度,单位入口流量增加引起的增量开始减小;同时地面管道及换热设备随着流体流量的增加,其流动阻力也必然增加,进而会导致由流动阻力带来的损失增加,所以SEGS入口流量也不宜过大。

图17 不同入口流量条件下SEGS的增量变化情况
4.7 入口水温对SEGS的影响

图18 SEGS平均出口水温和平均换热功率随入口水温的变化
图18所示为不同入口水温条件下SEGS的出口水温和平均换热功率随时间的变化。SEGS的出口水温与入口水温的变化联系密切,当入口水温提升时,出口水温也在提升,当入口水温由5℃提升至30℃时,相应的平均出口水温分别为43.3℃、45.1℃、46.9℃、48.7℃、50.6℃和52.4℃。与出口水温变化趋势相反的是,SEGS的平均换热功率随着入口水温的提升而下降。当入口水温为30℃时,单井平均换热功率已经低至938.1kW。可见SEGS的出口水温以及换热功率对入口水温的变化极其敏感,可以通过降低入口水温提升SEGS的换热功率。
5 结论

图19 SEGS在不同进口温度下的逐日增量
(1)相比DBHE,SEGS的换热能力得到了较大的提升,无论是短期运行还是长期运行,其性能都十分可靠。相比换热流体从外管流入由内管流出的运行方式,采用与之相反的流动方式可以使SEGS的性能得到充分地发挥。逆流形式的SEGS换热功率为1603kW,是深井换热器的2.2倍。
(2)人造热储的厚度对SEGS的换热能力有较大的影响。因为地温梯度的影响,SEGS的换热功率先随热储厚度增加而增加,之后略有减小。人造热储的厚度为100m时,SEGS的平均换热功率为900.2kW,储层厚度为300m时,SEGS的平均换热功率为1502.7kW。
(3)SEGS的换热功率随人造热储半径的增大而增大,而且其增大速度逐渐降低。热储半径由50m提升至90m,半径每增加10m带来的换热功率提升分别为102.7kW、67.0kW、43.8kW和29.2kW。考虑到建设费用,不能盲目扩大人造热储的半径。
(4)SEGS出口温度较高,流体从环空流出时会向浅层岩石散失热量,通过改变外管周围的保温性能可以减少这种热量损耗,当固井水泥热导率为0.1W/(m·K)和0.01W/(m·K)时,单井平均换热功率与热导率为0.8W/(m·K)相比,分别提升了61.3kW和109.5kW。保温带来的换热功率提升不高,实际建设时要考虑到保温成本的问题,可以不用过分强调外管保温效果。
(5)入口水温以及流量对SEGS的换热表现影响明显。入口水温越小,单井的换热功率越大,同时出口水温也会随之减小;入口流量越大,SEGS的单井换热性能越好,当入口水温不变时,存在一个入口流量可以使SEGS的出口水温最高。

