FSRQ 0208−512的光学波段长周期光变分析和色指数变化研究*
陆 林 张皓晶 任国伟 张 欢 晏培琳 马凯旋
(1云南师范大学物理系昆明650092)
(2厦门大学天文系厦门361005)
1 引言
类星体各个波段的光变时标是一个很重要的物理参数,天体的长周期光变可以帮助我们研究其轨道和转动问题[1],通过类星体的轨道和转动问题可以研究天体的中心黑洞质量、内部结构、辐射区域等问题[2],一般研究此类问题的方法[3–4]有结构函数法[5]、离散相关函数法(DCF)[6]、period4方法[7–8]、功率谱[9]、Jurkevich方法[10]、加权小波Z变换法(WWZ)[11]和蒙特卡洛模拟的LombScargle periodogram(LSP)方法[12]等.从SMARTS(The Small and Moderate Aperture Research Telescope System)收集到了平谱射电类星体(FSRQ)0208−512(红移z=1.003)[5]的准同时性光学波段近10 yr的数据.由于类星体光学波段的观测受天气、设备等多种因素的影响,观测数据在时间序列上不连续,光变周期的研究会有较大的误差,如何提高精度一直是该研究方向上的热点问题.在本文中首次将该天体光学波段的离散数据应用WWZ和蒙特卡洛模拟的LSP方法来研究相应波段的光变周期,为类星体的长周期光变研究找到了一种新方法,通过WWZ[11]和蒙特卡洛模拟的LSP方法可以很好地得到非平稳信号的周期,并给出了相应周期的置信度,在这两种方法中我们得到了光学B、V、R波段都存在约为396 d的光变周期,置信度超过3σ.并且我们知道当色指数越大时,颜色会显得较红,当色指数越小时,颜色会显得较蓝,通过研究色指数(B−V)与B星等关系,可以反映出天体的变亮或变暗时的颜色变化,我们就可以进一步研究其中的物理机制.
2 观测数据研究
如图1所示为来自于SMARTS数据库的FSRQ 0208−512光学B、V、R波段的光变曲线,去除了因为天气或设备等其他原因没有观测的无效数据点,图中采用了约化的儒略日(MJD)[13],定义为:

式中JD为原始数据中非约化的儒略日,图1中Magnitude表示各个波段的星等值.

图1 FSRQ 0208−512的光变曲线.蓝色为光学B波段的光变曲线,橙色为光学V波段的光变曲线,红色为光学R波段的光变曲线.Fig.1 The light curve of FRSQ 0208−512.The blue line represents the light curve in the optical B band,the orange line represents the light curve in the optical V band,and the red line represents the light curve in the optical R band.
可以看出这3个波段的光变曲线变化趋势大致相同,各个波段的星等变化情况如表1,其中B、V、R波段的星等分别用B、V、R表示.从表1中可以清楚看到B波段的变化幅度为3.271星等,V波段的变化幅度最小为3.227星等,R波段的变化幅度最大为4.303星等,由此表明V波段相对于其他波段来说光变比较平稳,R波段变化最剧烈.

为了更好地描述各波段的活跃程度需要将星等值转化为流量值,采用其他文献[13]中所给出的流量与星等转化关系[14],将以上的3个波段的星等值转化为流量值.已知:

F为每一个波段所对应的流量值,m代表对应波段的星等值,在得到各个波段的流量之后可以采用光变指数A[15–16]来描述天体的活跃程度,光变指数越大代表天体越活跃:
式中,Fmax为相应波段的最大流量值,Fmin为相应波段的最小流量值.
在表2中给出了相应波段的最大流量值、最小流量值和光变指数,从表2中可以看出FSRQ 0208−512在光学B波段和V波段的变化幅度基本一致,并且在各个波段都较为活跃,尤其在R波段的变化最为活跃.

表1 FRSQ 0208−512各个波段的光变曲线变化情况Table 1 The light curve variation in each band of FRSQ 0208−512

表2 各个波段的流量的最大值和最小值和光变指数值Table 2 The maximum and minimum value of flux and the value of variability index in each band
3 光变曲线的长周期分析
从SMARTS数据库中获得星等数据之后,通过流量与星等转化公式得到各个波段的流量数据,并且从光变指数A[15–16]来看在光学波段都是很活跃的.接下来我们将采用蒙特卡洛模拟的LSP方法和WWZ[11]来计算各个波段的周期和相应的置信度.
3.1 用蒙特卡洛模拟的LSP方法分析长周期光变
计算隐藏在噪声中的周期性信号是天文数据时间序列分析中的一个重要目标.蒙特卡洛模拟的LSP[12]方法可以对非均匀采样的时间序列周期图进行相位修正[12],能够在一定范围内对非均匀采样的时间间隔引起的误报周期进行处理[12].因此,蒙特卡洛模拟的LSP[12]方法能很好地寻找隐藏在噪声中的准周期振荡光变.现在假定有这么一组时间序列x(tj),(j=1,2,3,···,N,N为数据的个数)[17],则时间序列的蒙特卡洛模拟的LSP的功率谱由以下的公式[17]所给出,Px(ωj)是以角频率(ωj=2πνj)为变量的功率谱函数,νj为所试探的周期频率,基本形式如下:

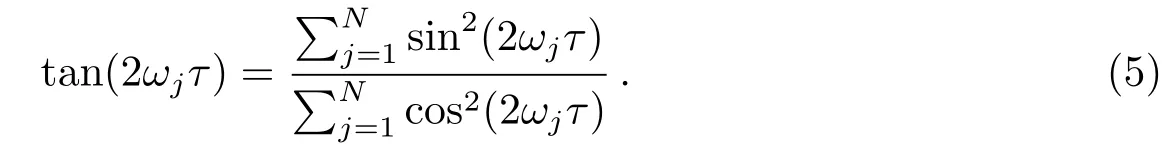
图1的光变曲线是一个非均匀的时间序列,要得到里面隐藏的周期非常困难,我们采用蒙特卡洛模拟的LSP方法来计算相应的周期和置信度,并且以这种形式使得周期图分析完全等价于正弦曲线对数据的最小二乘拟合.现在我们先对转化为流量之后的数据进行对数幂律拟合,得到蒙特卡洛模拟的LSP方法计算置信度所需参数幂律指数α[18].如图2为各个波段的对数幂律拟合和α的值[18].
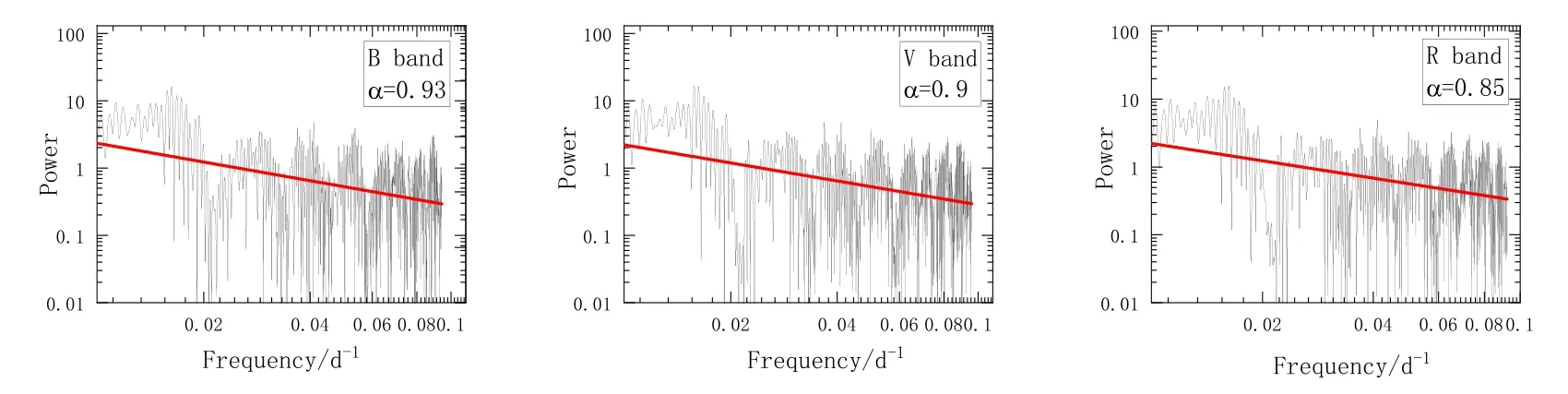
图2 FRSQ 0208−512光学B、V、R波段的幂律的对数拟合Fig.2 The logarithmic fitting of power law in optical B,V and R bands of FRSQ 0208−512
通过以上的对数幂律拟合,我们得到了各个光学波段的α值,在得到每一个波段的α值后我们需要将这些指数一一代入到蒙特卡洛模拟的LSP中,去计算出每条光变曲线的置信度和相应的周期.
图3中分别为光学B、V、R波段的蒙特卡洛模拟的LSP功率谱和相应的置信度.通过原始信号的功率谱与所给出的蒙特卡洛模拟的LSP功率谱进行对比,当出现超过3σ的周期频率时,可以计算出相应的周期,即所超过3σ的频率位置为相应原始信号的周期频率.图3中纵轴为相应波段的功率谱的对数值,横轴为相应的频率,单位为d−1,图中的红色曲线代表了相应波段的功率谱变化情况,黑色的曲线代表3σ即99.7%置信度,紫色的曲线代表2.6σ即99%置信度,橙色的曲线代表2σ即95%置信度,当图中出现了峰值高度最高超过3σ置信度,就可以找到了峰值点所处的频率值,对此处的峰值频率取倒数即为此波段置信度大于3σ的候选周期.
由图3我们看到了在光学B、V波段都存在一个置信度超过3σ的峰值,在光学R波段存在两个置信度超过3σ的峰值,相应的峰值频率保留4位小数分别为B波段(0.0026 d−1)、R波段(0.0026 d−1,0.0095 d−1)、V波段(0.0026 d−1).所以B、V波段相应的周期约为396 d,R波段的周期约为396 d和1052 d,但是在天体的准周期运动中,一般只有一个周期,所以在R波段的两个候选周期中有一个是伪周期,因此我们需要使用其他方法来对3个波段的数据进行计算,进一步确定真实周期.

图3 FRSQ 0208−512光学B、V、R波段的蒙特卡洛模拟分析结果Fig.3 The analysis result of Monte Carlo simulation in optical B,V and R bands of FRSQ 0208−512
3.2 用小波分析和傅里叶变换方法分析长周期光变
在经典的时间频率分析中一般采用傅里叶变换和小波分析.在使用傅里叶变换时为了求出某个频率ν的频谱f(ν),需要对全部时间段的信号f(t)进行积分运算.如果在任何有限的频段频谱f(ν)上都不能够确定这一小段内的信号f(t)时,也必须要对全频段进行积分,但是这样就会平滑掉非平稳信号中的突变成分,而且傅里叶变换中的突变成分可能还会存在吉布斯效应.在天文数据中往往获得的都是非等间距的离散数据,使用傅里叶变换和小波变换来分析天文数据时需要对数据进行插值处理,这样对数据的真实性有很大的损害[9],并且在使用傅里叶变换来处理这些非等间距的数据时可能还会出现伪周期,所以在基于小波变换的基础上Foster[19]提出了WWZ,这样不仅可以更加有效地处理非等间距的时间序列并发现候选周期,还可以在一定程度上反映出周期的稳定性.
WWZ是将时间序列投影到3个正交归一的时间序列坐标基函数上,即φ1(ti)=1,φ2(ti)=cos[ω0(ti−τ0)],φ3(ti)=sin[ω0(ti−τ0)],(i=1,2,3,···,N),并在投影上做了统计加权ωi=exp[−cω20(ti−τ0)2],将数据的不均匀通过权重调节,避免了周期分析受到数据过密的影响,其中使用的母函数为Morlet小波[19],WWZ中的参数Z定义为:

其中Neff为有效数据点个数,Vx、Vy分别为观测数据和模拟函数的加权变量.这个等式满足F分布,分子、分母的自由度分别为Neff−3和2.Neff、Vx、Vy表达式分别如下:

式中,x(ti)、y(ti)为时间序列即相应的模型函数,ωi为投影上的加权统计量,c为衰减因子,τ0为时移,ω0为尺度因子,ωλ为对应的测试频率(λ=1,2,3,···,n).
图4为FSRQ 0208−512的WWZ分析结果,左边红色显示了相应周期频率出现的位置,右边红色曲线显示相应波段的WWZ功率谱,可以得到周期频率为:B波段(0.0026 d−1)、R波段(0.0026 d−1)、V波段(0.0026 d−1),所以得到对应的周期都为396 d.在WWZ功率谱中,我们通过检验零假设虚假警报概率(FAP)[20–21]来估计相应周期的置信度,其相应的公式为[20–21]:P(>z0)=1−(1−e−z0)M,M为数据点的总个数,e为自然对数底数,z0为相应周期频率的功率,当虚假警报概率越小时所对应周期的置信度越高,结合以上的数据我们得到3个光学波段的FAP分别为:PB=2.5×10−28、PV=3.4×10−29、PR=3.8×10−26.可以看到3个波段的虚假警报概率远远小于以上对应的0.003的置信水平,所以对应的周期置信度大于3σ.
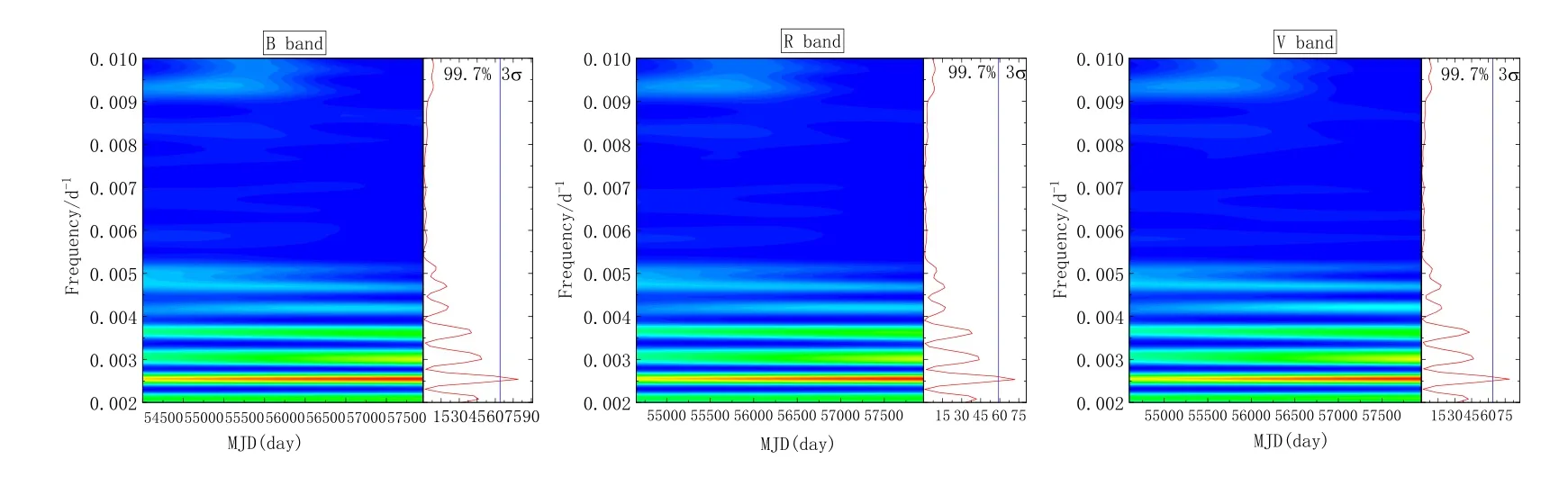
图4 光学B、R、V波段小波分析结果和相应的周期频率Fig.4 The Wavelet analysis results and corresponding periodic frequency in the optical B,R and V bands
在WWZ中揭示了相应周期频率的稳定性,通过LSP的蒙特卡洛模拟我们可能会得到相应周期的置信度,但是无法体现出相应周期频率的稳定性,所以在蒙特卡洛模拟的LSP方法中所得到的周期可能会有好几个,其中可能有些周期是不稳定的伪周期.通过WWZ方法,我们可以得到相应的周期频率,并且体现出相应的稳定性.在本文中我们还使用FAP方法,来获得相应周期的置信度,所以结合上面的分析,FSRQ 0208−512 3个光学波段的长周期为396 d,约为1.08 yr.
4 色指数
天体的颜色变化也是我们感兴趣的问题之一,一般采用色指数(B−V)来研究天体的颜色变化,同样我们也需研究色指数的变化趋势,当色指数较大时颜色较红,当色指数较小时则颜色较蓝.
从图5中可以看出FSRQ 0208−512光学波段(B−V)10 yr来的变化也较活跃,可以看到(B−V)有少量剧烈变化,发生大幅度变化的时间与前面的颜色变化并没有相隔太长时间,所以我们认为这不是因为观测数据缺失造成的,可能是在很短时间内产生了大量高频辐射导致的.
(B−V)的变化趋势也是人们很感兴趣的问题之一,因为色指数的变化反映了天体的颜色特征,一般人们会选取某个可见光波段的星等值与(B−V)做一元线性拟合,在本文中选取B波段星等与(B−V)做线性拟合.

图5 色指数(B−V)的变化曲线Fig.5 The variation curve of color index(B−V)
图6中的红色线代表色指数(B−V)与星等B的一元线性拟合直线,相应的线性拟合方程为:

所取样本点数为K=615,相关系数为r=0.114,置信水平为Pr=0.00456.通过以上的结果,我们得到了(B−V)与B的正相关关系,所以当B越小时(B−V)越小,即越亮越蓝.这个结果与Rani等[22]的结果一致:喷流中的激波模型表明激波沿着喷流传播,并且和一个高能电子区域发生作用,在激波后面的不同距离产生不同颜色的辐射,和更低频率的辐射相比,同步辐射产生的高能光子出现更快并且更接近激波波前,所以导致了色指数的变化,使得高频率的辐射变化幅度大于低频率变化幅度,导致了变亮时候变蓝,即越亮越蓝.
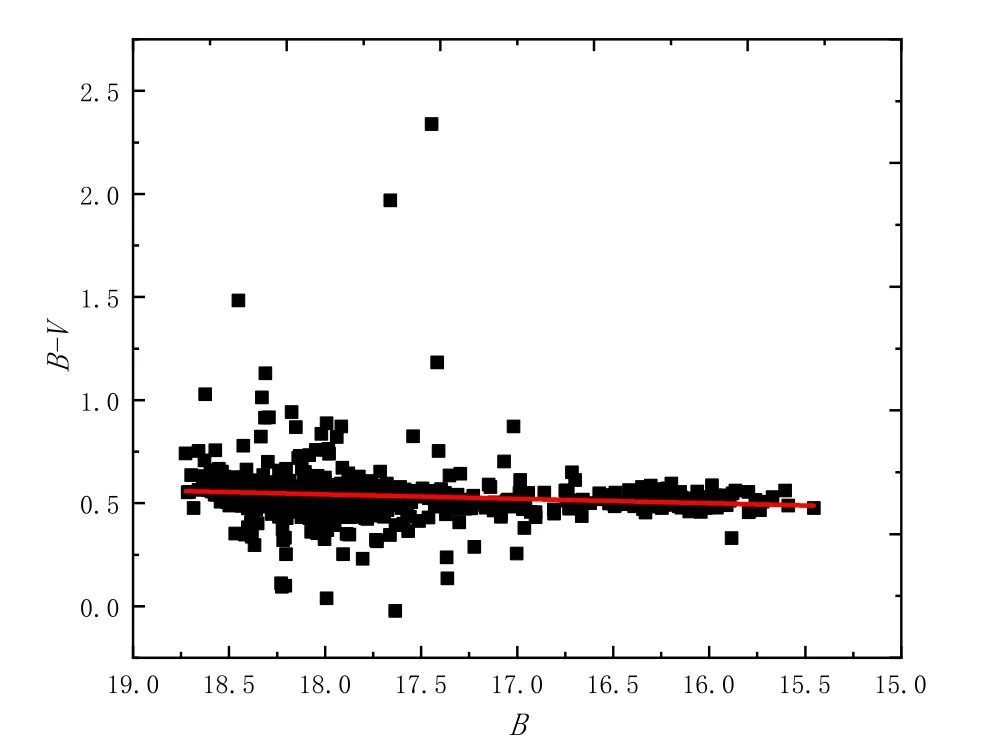
图6 (B−V)和B的线性拟合Fig.6 The linear fitting between(B−V)and B
5 中心黑洞质量和辐射区半径
5.1 中心黑洞质量
中心黑洞也是人们极为感兴趣的课题,对于类星体来说中心有一个超大质量的黑洞,很多的辐射现象是由中心黑洞引起的.在这部分我们通过长时标光变来计算其中心黑洞的质量,利用其他文献中[23]给出的关系:

式中α0.1是以0.1为单位的粘度参数,M6=M/106M⊙,M为中心黑洞质量,是吸积率,µ是广义应力张量参数.当µ=0.5时,,其中ME是爱丁顿吸积率,ε是吸积效率.爆发时间间隔主要取决于µ.Horiuchi等[24]建议,µ=0.5时磁场的逃逸速率会更低,此时,热极限周期时间为tcyc=2tburst,所以:

当α0.1=1、µ=0.5、时,我们采用3个波段1.08 yr的周期得到中心黑洞的质量约为0.12×106M⊙.这个结果是由于利用薄吸积盘理论的分析方法,没有考虑到黑洞自旋的影响,所以相比一般的平谱射电类星体的中心黑洞质量偏小.
5.2 辐射区半径
对于类星体的长周期光变现象目前还没有合适的物理模型,为了解释这个问题提出了双黑洞模型[25–26]、螺旋喷流模型[27–28]和薄盘的热不稳定性等[29].Wallinder等人利用薄盘不稳定性分析长周期T[29],通过长周期T可以确定出热不稳定性产生的区域[29]:

6 结论
在对FSRQ 0208−512光学波段的研究中,本文使用WWZ和LSP这两种方法相结合,分别给出了各个波段周期的稳定性并计算了周期置信度,我们发现:
(1)通过两种方法都在光学B、V、R波段发现了396 d(1.08 yr)的光变周期.但是在蒙特卡洛模拟的LSP方法中我们还得到了R波段存在1052 d(2.88 yr)的周期.在蒙特卡洛模拟的LSP方法中我们得到的是周期的置信度.而WWZ反映了周期的稳定程度,此处在蒙特卡洛模拟的LSP方法中得到的周期并没在WWZ中持续出现,所以本文得到的R波段1052 d的周期是伪周期.综合以上结果,我们所得到的3个波段的周期应为396 d.这个约396 d的周期在蒙特卡洛模拟的LSP方法中的置信度为99.7%~(3σ),在WWZ中的置信度也超过了99.7%~(3σ),而地球绕太阳的周期约为365 d,假设用地球绕太阳的周期作为某观测效应的真实周期,那我们所得结果相对于地球自转的相对误差为,式中Tresult为我们所计算的周期最终结果,Tearth为地球的公转周期,则我们所得最终结果和地球公转周期差值的绝对值为:|∆T|=|Tresult−Tearth|,那么|∆T|相对于地球公转周期的相对误差为:

相对误差不小于8%,远远超出了误差界,所以这个约1.08 yr的周期不可能是地球绕太阳365 d公转周期的观测效应产生的,可以排除地球绕太阳运行的影响.并且在文献[5]中给出了2008—2011年期间在光学波段观测到了3次爆发,因此以上的结果是可靠的;
(2)在对光学色指数(B−V)的研究中,色指数(B−V)与星等B做一元的线性拟合,置信度Pr=0.00456、相关系数r=0.114,由于B−V=kB+C是正相关的线性拟合方程,其中k为斜率、C为截距,当B星等越小时(B−V)就越小,FSRQ 0208−512表现为越亮越蓝;
(3)对于中心的超大质量黑洞,通过其他文献所给出的1.08 yr长周期与黑洞质量公式,结合本文3个波段共同的长周期数据我们得到中心黑洞质量M=0.12×106M⊙,辐射区半径RM=1.052×108km.由于是利用薄吸积盘理论的分析方法,没有考虑黑洞自旋的影响[23,31–33],所以比一般FRSQ中心黑洞的质量小.若使用其他方法[31–33],计算的黑洞质量约为108–109M⊙量级.但在本文中,目前此天体的观测数据较少,理论模型研究受到参数限制,本文方法不失为一种研究中心黑洞质量较为有效的方法.本文计算得到的辐射区半径相比其他文献[30]所给出的辐射区半径在相应的施瓦西半径下要大一个量级左右,由于其他文献[29]中所采用的黑洞质量要比本文中所用的黑洞质量大了一个数量级,当黑洞质量变小时施瓦西半径也变小,而同一个天体要产生相同的能量,相应的产能区要变大,所以此处我们所得的辐射区半径是合理的.
致谢感谢编辑部和审稿人在审阅本文时指出的问题和提出的宝贵修改建议.

