疏散星团M67成员星的两点相关分析*

郭文瀚 罗智坚 束成钢

(1上海包玉刚实验学校上海201620)

(2上海市星系与宇宙学半解析研究重点实验室上海200234)

(3上海师范大学数理学院上海200234)

1 引言

随着观测资料的不断扩大,现代数理统计方法在天文研究中扮演了越来越重要的角色,如两点相关函数、最近邻分析、渗流、功率谱分析、BA(Binning Analysis)和KS(Kolmogorov-Smirnov)检验、团分析和多重性函数等[1–11].其中,两点相关函数和渗流的应用较广泛[1–2,12–13].两点相关函数是研究星团中恒星空间分布情况的一种重要方法,它可以描述星团内恒星的空间分布与均匀随机分布之间的差别,对团星的成团性做出判定.渗流则主要用于探测样本中链状和网状结构的分布,对于样本的成团性并不敏感.本文的主要目的是探讨M67疏散星团中恒星的空间分布情况和成员星的成团性,故采用两点相关函数来进行统计研究.

与球状星团相比,疏散星团是一种中心聚度相对较低的恒星集团,由数十颗至数千颗恒星组成,外形较不规则;部分老年疏散星团呈近球形,中心聚度相对较好.一般来说,疏散星团的成员星有共同的起源,他们有相似的年龄和化学组成,由于疏散星团距离较近,许多基本天体物理参量的测量更为准确,它们的年龄、距离、金属丰度、自行等相对来说也更方便测定,有助于人们对恒星和银河系的结构及演化进行深入了解.疏散星团中成员星的确定方法已经相当成熟[14],许多疏散星团中也有足够数量的成员星,这为成员星的两点相关函数分析打下了良好的基础.本文将从最新公布的WEBDA(the Web version of Base Donn´ees Amas)数据库中收集疏散星团M67的观测资料进行两点相关函数分析,讨论其恒星的空间分布和动力学演化情况.

2 样本

WEBDA疏散星团表[15]是研究疏散星团十分重要的资料,由奥地利维也纳大学天文研究所编制而成,其中包括了许多疏散星团的测光和测谱数据.M67(NGC2682,α2000=8h51m18s,δ2000=11°48′.0)是其中被研究得最多的老年疏散星团之一,位于巨蟹座,年龄约为3.2×109–5×109yr[16],距离地球约800–900 pc[17],与银盘面的倾角约为15°[15].M67的成员星较为丰富(～1000颗[18]),距离也近,因而被广泛用于开展疏散星团结构与演化的研究.

由于投影效应的影响,星团观测的天区通常混有不同程度的场星污染.如何准确判定星团的成员星是所有星团研究工作的基础.通常人们利用观测天区中恒星的运动学资料(自行和视向速度)来去除场星的污染,从而相对准确地判定星团的成员.Sanders[19]根据恒星较高精度的自行速度资料,利用最大似然法最早完成了对M67所在天区B波段星等亮于17等的1866颗恒星的成员判定,并通过分析恒星的相对自行分布得出了1571颗成员星的成员概率,被收录到了WEBDA星团表中.此后,Girard等[20]、Zhao等[14]和赵君亮等[21–22]在Sanders[19]方法的基础上对成员星判定方法作了一定的改进,并对M67星团成员星重新进行了判断.但Girard等人只对M67天区中较亮的663颗恒星的成员概率进行了判别[20],而Zhao等[14]和赵君亮等[21–22]也只对M67区域内1067颗恒星进行了判别[14,21–22],数量较Sanders[19]少,且成员星的判定结果与Sanders[19]基本一致.近年来,随着Gaia巡天数据的陆续释放,基于Gaia空间高分辨率数据为基础的疏散星团成员星判定工作也取得了很大进展,如基于DR1和DR2数据的Cantat-Gaudin等[23–24]的工作及文献[25–26]等.但对于视差及自行测量,由于观测的历元差相对较短,Gaia仅对G波段星等亮于15等的亮端恒星具有高精度的观测.此外,利用Gaia数据对疏散星团成员星的判定大多是基于机器学习的聚类算法,如UPMASK(Unsupervised Photometric Membership Assignment in Stellar Clusters)[26]和RF(Random Forest)[24]等方法,与经典的、相对成熟可靠的Sanders方法具有较大不同.因此,本文采用WEBDA M67星表中Sanders[19]给出的1571颗恒星的成员概率,选取成员概率大于0.6的恒星作为M67的成员星进行研究,总共有451颗.这451颗恒星的成员概率之和为409,因而统计上可能混入团星的场星数为42颗,约占团星总数的9%.

3 两点相关函数的定义

如Schneider[27]和Mo等[28]所指出的,两点相关函数是用来描述天体分布状况的一个重要方法.空间两点相关函数P的定义为:在距离为r的两个体积元δV1和δV2中,同时发现两个天体的概率:

一般来说,两点相关函数有两种,一种为角相关形式,描述天体在天球上投影的分布,称为角两点相关函数;另一种表征天体在空间中的分布,称为空间两点相关函数.本文所讨论的两点相关函数指的是角两点相关函数,其计算公式为[1]:

其中,DD(θ)为样本中恒星间角距离在θ→θ+δθ的数目,RR(θ)为在同一区域内均匀随机分布的样本中,数据点间角距离在θ→θ+δθ的数目,〈RR(θ)〉表示对多次随机取样进行平均(本文随机取样1000次).我们用Shimazaki和Shinomoto[29]的方法计算了最佳的Bin-size取值,并根据两点相关函数的边缘效应[30–31],对δθ作了对数修正.根据计算出的ξ(θ),可以得出样本中天体分布相对于均匀随机分布的偏离程度与偏离状态.若ξ(θ)>0,样本为正相关,出现成团现象;反之,若ξ(θ)<0,样本呈负相关,出现空洞现象[27];ξ(θ)=0表示样本为均匀随机分布.对于ξ(θ)估计,我们可以很好地采用泊松误差[28]

来估计两点相关函数ξ(θ)的误差.在本文中,两点相关函数的角相关形式中所有的角度单位取′.

4 自相关分析

自相关分析用于检验一个样本是否在空间上成团.通常,样本的两点相关函数可以表示为θ的函数,并满足幂律分布[1]:

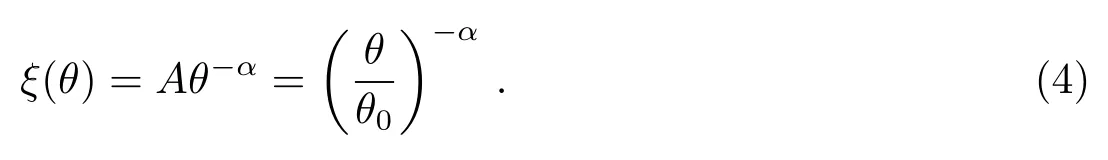
其中,A为相关强度,θ0为相关尺度,α为相关指数,A、θ0和α可以通过对上式取对数后进行线性回归拟合得到.

表1和图1(a)是M67中451颗成员星的两点自相关函数的计算结果.由于星团核区动力学演化以及两个恒星间距离不能太近因素的影响,在θ很小时(～3′)两点相关函数会产生偏离.本文仍然将最小θ值的数据点显示在图上,以“×”表示,但在进行线性回归拟合时将该数据点舍去.拟合时所用数据点用“°”表示,我们已根据误差考虑了每个数据点的权重(下同),拟合结果用虚线表示.

表1 M67样本成员星、场星的自相关分析Table 1 Self-correlation analysis of M67 member stars and field stars

图中可以看出,M67的自相关性非常好,相关强度为23.13±3.60(′)α,相关尺度为(24.30±6.71)′,置信水平大于99%.图1(b)是M67天区内,除去451颗成员概率大于0.6的成员星后的1118颗场星的两点相关函数.从图中可以看出,场星的自相关性非常低,相关强度为0.56±0.17(′)α,相关尺度为(0.28±0.10)′.对于均匀分布的场星,ξ(θ)理论上应该在0附近振荡,本文中ξ(θ)不为0的原因主要由银河系自身其他结构特征引起,场星自身成团信号较团星低一个量级以上,故本文的自相关分析是可信的.

图1 (a)M67全部成员星的自相关分析拟合;(b)场星的自相关分析拟合.Fig.1(a)Self-correlation analysis and fitting of M67 member stars;(b)Self-correlation analysis and fitting of field stars.

在星团形成和动力学演化过程中,团星间的动能均分会导致成员星之间出现能量(动能)交换.小质量成员星的运动速度将逐渐增大,大质量成员星的运动速度则逐渐减小.经过充分的动力学演化,在达到维里平衡后,星团将表现出空间质量分层效应和速度质量分层效应[32].McNamara和Sekiguchi[33]对疏散星团的空间质量分层有过详细的介绍.疏散星团的空间质量分层意味着不同质量区间的成员星会出现不同的径向分布密度轮廓,大质量成员星相对于小质量成员星有更大的中心聚度.

为了研究M67的质量分层效应,我们利用BATC(Beijing-Arizona-Taipei-Connecticut)大视场多色巡天3890˚A波段的测光数据[34],将M67的团星分为了3个不同光度范围的子样本,并分别计算了每个子样本的自相关函数.其中,子样本A有131颗恒星,星等范围mA≤13.3;子样本B有156颗恒星,星等范围mB∈(13.3,14.3],子样本C有107颗恒星,星等范围mC∈(14.3,15.3].表2和图2是各个子样本的自相关情况.

表2 M67中不同光度子样本的自相关分析Table 2 Self-correlation analysis of M67 member stars based on magnitude

从表2和图2(a)–(c)可以看出,M67不同光度范围的3个子样本均具有强自相关性,两点相关函数都能用幂律形式较好地拟合.其中,子样本A的自相关性最强,相关强度大于20(′)α,子样本B和C的相关强度值则相对较小,均小于10(′)α.从表2和图2中还可以看出,随着光度的减小,从子样本A到子样本C,两点自相关函数的相关强度和相关指数亦逐渐减小,说明M67的亮星与暗星具有明显的分维,成员星呈现出明显的空间质量分层效应,亮星较暗星具有更强的中心聚度.

图2 M67不同光度子样本的自相关分析拟合.(a)子样本A;(b)子样本B;(c)子样本C.Fig.2 Self-correlation analysis and fitting of M67 member stars based on magnitude.(a)subsample A;(b)subsample B;(c)subsample C.

团星的空间质量分层现象是星团经历长时间动力学演化的结果.Bica和Bonatto[35]定义了一个演化参数:

来衡量星团的动力学演化程度,其中,tc为星团的年龄,tr为星团的弛豫时标,即星团达到维里平衡所需要的时间.τ值越大,星团的动力学演化越充分.根据Chandrasekhar[36]对弛豫时标计算的公式:

其中,N为星团中恒星的个数,¯m为团星的平均恒星质量与太阳质量的比值,为星团的半光度半径,单位为秒差距[37],我们可以算出,M67的弛豫时标约为3×107yr[38].由于M67的年龄约为4×109yr,故演化参数τ≫1.这表明M67已经经历了长期的动力学演化,出现空间质量分层现象是合理的.

5 交叉相关分析

两点交叉相关函数常用于分析几组样本相互之间的关系.通过交叉相关分析能更深入地了解样本的空间成团性.一般地,两点交叉相关函数可通过下式计算:

其中,DD12(θ)是任意两组样本中,恒星间角距离为θ→θ+δθ的点对数目.

与两点自相关函数类似,两点交叉相关函数ξN12(θ)一般也满足幂律分布[1]:

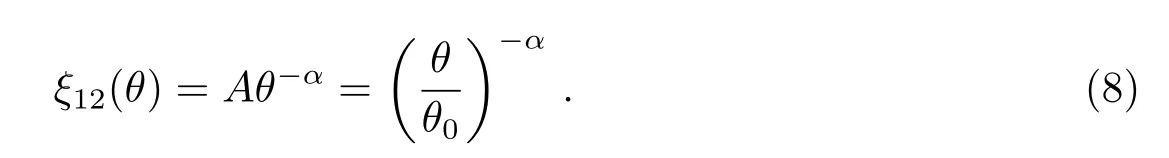
式中,A、θ0和α3个参数也可以通过对上式取对数后进行线性回归拟合得到.

M67中3个子样本A、B和C之间的两点交叉相关分析的计算和拟合结果见表3和图3.图3(a)、(b)和(c)中的虚线分别代表对子样本A–B、A–C和B–C的交叉相关分析的幂律拟合.

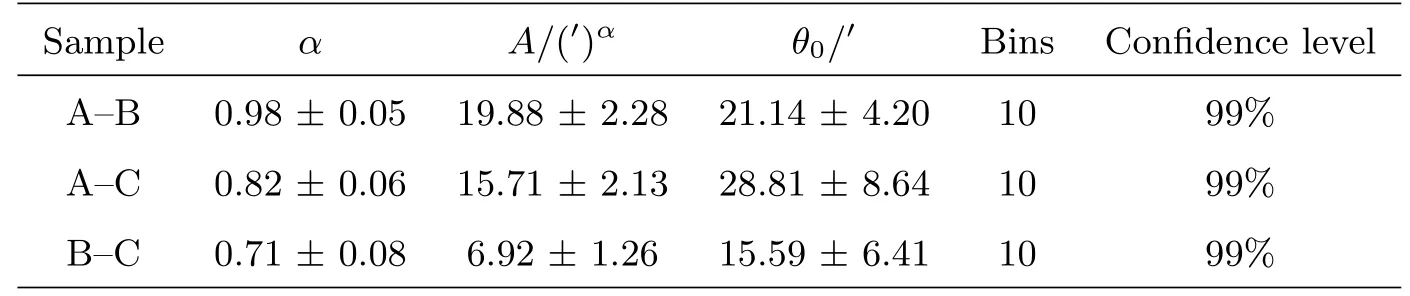
表3 M67各个子样本的两点交叉相关分析Table 3 Cross-correlation analysis of M67 member stars based on magnitude

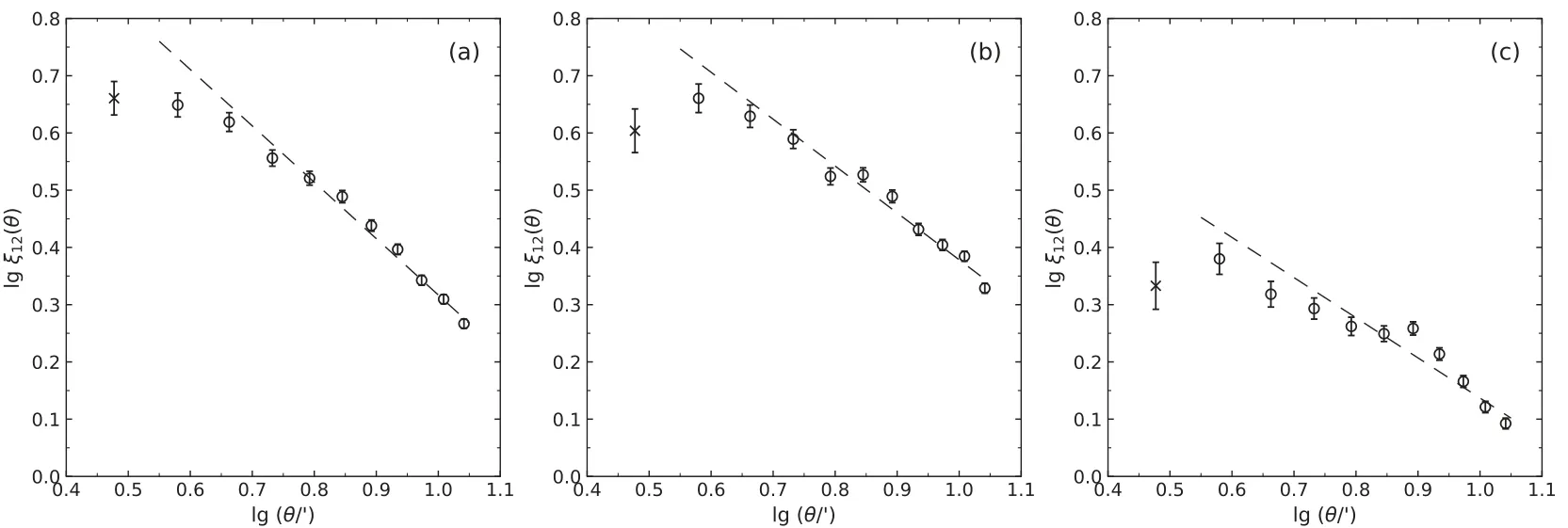
图3 M67成员星子样本的交叉相关分析拟合.(a)子样本A–B;(b)子样本A–C;(c)子样本B–C.Fig.3 Cross-correlation analysis and fitting of M67 member stars.(a)subsample A–B;(b)subsample A–C;(c)subsample B–C.

由表3和图3可知,M67中各个子样本之间存在明显的交叉相关性,说明M67中不同光度的成员星即使有不同的自相关强度和指数,但他们没有表现出绝对的空间质量分层,不同光度的成员星之间相互交织、相互渗透.同时,从表3和图3还可以看出,各个样本之间的两点交叉相关函数存在一定的差异.子样本A与子样本B之间的交叉相关强度和相关指数最大,分别为19.88±2.28(′)α和0.98±0.05,而较暗的子样本B和C之间的交叉相关强度和相关指数相对最弱,分别为6.92±1.26(′)α和0.71±0.08,说明随着星等的变小,M67子样本间的交叉相关强度逐渐减弱,相关指数也逐渐变小,这从另一角度说明了亮星相对于暗星具有更强的成团性,M67中存在空间质量分层现象.

6 总结与讨论

本文利用WEBDA数据库中归档的老年疏散星团M67的观测资料,对M67成员星进行了两点相关函数分析,讨论了团星的空间分布情况.在研究中,对M67的成员星判定采用了Sanders[19]的研究结果,并取用了成员概率p≥0.6作为团星的选择标准.同时,本文还利用Burstein等人给出的BATC大视场多色巡天3890˚A波段的测光数据[34],将M67的团星分成了3个不同星等(质量)范围的子样本,并对各个子样本自相关函数的差异和子样本间的交叉相关性进行了分析,探讨了M67团星的空间质量分层效应与动力学演化规律.

我们的研究结果表明,M67全体成员星的两点自相关函数能很好地用幂律形式来描述,其成员星的空间分布具有强成团性和自相似性.此外,按光度区间划分的3个子样本的两点自相关函数也能很好地用幂律形式来描述,但不同光度子样本的两点自相关函数之间存在明显的差异,亮星子样本比暗星子样本有更强的自相关强度和更大的自相关指数.这说明M67中大质量的成员星(亮星)具有更强的成团性及中心聚度,该星团在空间分布上已经出现了明显的质量分层现象.通过计算M67的弛豫时标并和年龄进行对比发现,M67的演化参数[35]τ≫1,表明在其演化过程中已经经历了充分的动力学演化,M67在两点相关函数统计分析上表现的空间质量分层现象从物理上来说是合理的.

本文进一步的研究还表明,M67中不同光度范围的子样本间的两点交叉相关函数也可以很好地用幂律形式来描述,表明不同光度区间的恒星之间没有表现出绝对的空间质量分层,亮星和暗星相互交织、相互渗透.此外,各子样本之间不仅存在明显的交叉相关性,且随着光度的减弱,交叉相关强度及相关指数也逐渐减弱,再次从另一方面证实了空间质量分层效应的存在.