我国西部罗兰台站定位性能分析*

燕保荣 李 云 郭 伟 华 宇

(1中国科学院国家授时中心西安710600)

(2中国科学院精密导航定位与定时技术重点实验室西安710600)

1 引言

罗兰导航系统(Long range navigation)是一种陆基、低频、脉冲相位调制的远程无线电导航系统[1],它以覆盖范围较广、传播稳定、抗干扰性能好的特点[2]著称,是全球卫星导航系统(Global Navigation Satellite System,GNSS)的有效备份和补充[3–5].近年来,卫星导航系统的缺陷日益突出,导致GNSS定位授时服务中断的事件频频发生,给国家经济和安全带来极大威胁.罗兰系统以其极强的抗干扰性能和较稳定的信号特征成为卫星导航系统补充和备份的最佳选择.鉴于此,各国都在积极发展以罗兰系统为代表的陆基无线电导航系统,以期在GNSS中断的情况下能够提供人们需要的定位授时精度.美国和英国的科研工作者针对罗兰系统定位授时精度差的特点,结合差分方法开展了附加二次时延的修正研究,在港口区域精密进近领域达到了10 m(95%)的定位精度[6–7].韩国也对附加二次时延进行了大量的研究工作,除此之外,还开展了增补台站以及信号处理方面的讨论[8–10].我国罗兰系统的发展以位于蒲城的长波发播台为代表,主要实现覆盖区域内的长波定时.为提高定时精度,近年来也不断开展了包括授时方法、接收机信号处理等相关方面的研究工作[11–15],甚至还开展了罗兰与卫星相结合的导航定位方法研究[16].位于我国东部海岸的罗兰台链,能够为近海区域的船舶提供定位服务[17–18].但作为卫星系统的有效备份,我国现有罗兰台站难以满足需求.鉴于我国幅员辽阔,罗兰发播台站主要集中在中部及东部海岸的现状,我国于2016年12月批复了国家基础设施建设项目“高精度地基授时系统”的建设规划,通过了在我国西部地区增补3个罗兰发播台站的建议,以期实现罗兰信号在我国的全面覆盖.

尽管在我国西部地区增补3个罗兰发播台站的目的是实现全国范围内的罗兰授时,但是将罗兰台站用于陆基定位也是未来发展的必然方向,可以成为我国北斗卫星导航系统的有效补充.本文以我国西部将要建设的3个罗兰台站为研究对象,以罗兰传播特性为出发点,结合定位授时算法和罗兰接收机的接收特点,分析罗兰系统在西部地区的定位性能,为罗兰系统的进一步发展提供理论基础.

2 罗兰信号传播与定位

2.1 罗兰信号传播时延

罗兰信号的载波频率为100 kHz,载波信号沿地球表面传播的形式为地波.信号由发射天线到达接收天线所经历的时间延迟称为罗兰信号的传播时延,其表示形式为:

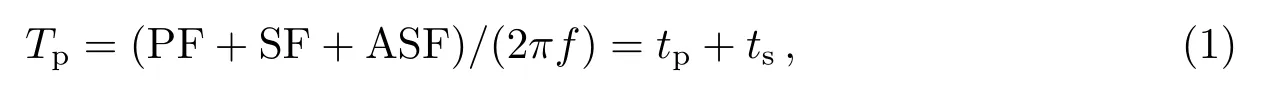
(1)式中,PF为一次相位因子(Primary Phase Factor),是指信号从发射台到接收点在大气中传播的相位延迟.SF为二次相位因子(Second Phase Factor),是指信号从发射台到接收点在纯海水路径中传播相对于空气中传播增加的相位延迟;ASF为附加二次相位因子(Additional Secondary Factor),指信号传播通过陆地相对于海水路径增加的相位延迟[19–20].f为载波频率,单位为Hz,tp为一次相位因子所对应的时间延迟,称为基本时延[21];ts为二次相位因子和附加二次相位因子所对应的时间延迟,即二次时延与附加二次时延之和.针对这两种传播时延,通常利用简化的模型[22]计算.当长波信号是在真实的大气中传播时,大气的折射率ns会对传播的授时信号产生影响,而大气折射率又是随时间和空间变化的量,会引起授时信号传播速度和方向的变化,从而影响传播时延.按照我国电磁波行业的标准将ns的平均值取为:ns0=1.000315.传播路径的距离可以根据收发两点的精确坐标按照标准椭球的大地线距离进行计算,用Rd表示.基本时延tp就可以表示为:

(2)式中,c表示真空中的光速,其值为:c=2.99792458×108m/s.ts反映了真实传播路径与大气传播中时间延迟的差异,由真实传播路径上衰减函数的相位表示:

(3)式中,w=2πf,是信号的角频率,单位为rad/s.argW是地波衰减函数W的相位,单位为rad.通常W与f、Rd、传播路径上的相对等效介电常数εe、等效电导率σe等参数有关,表示为W=W(f,Rd,εe,σe).根据国际电信联盟(International Telecommunication Union,ITU)(原国际无线电咨询委员会)关于大地传播类型的划分,7种典型地面类型分别为:平均海水、良导电地、潮湿地面、平均陆地、较干燥地、干燥地、甚干燥地,相应的相对介电常数、等效电导率等参数的取值见表1.依据表中的相关数据,计算了不同地面类型中二次时延与附加二次时延的和,即ts,ts与距离的变化关系如图1所示.从图1中可以看出,随着传播距离的增加,各种地面类型中的二次时延和附加二次时延的和也增加.

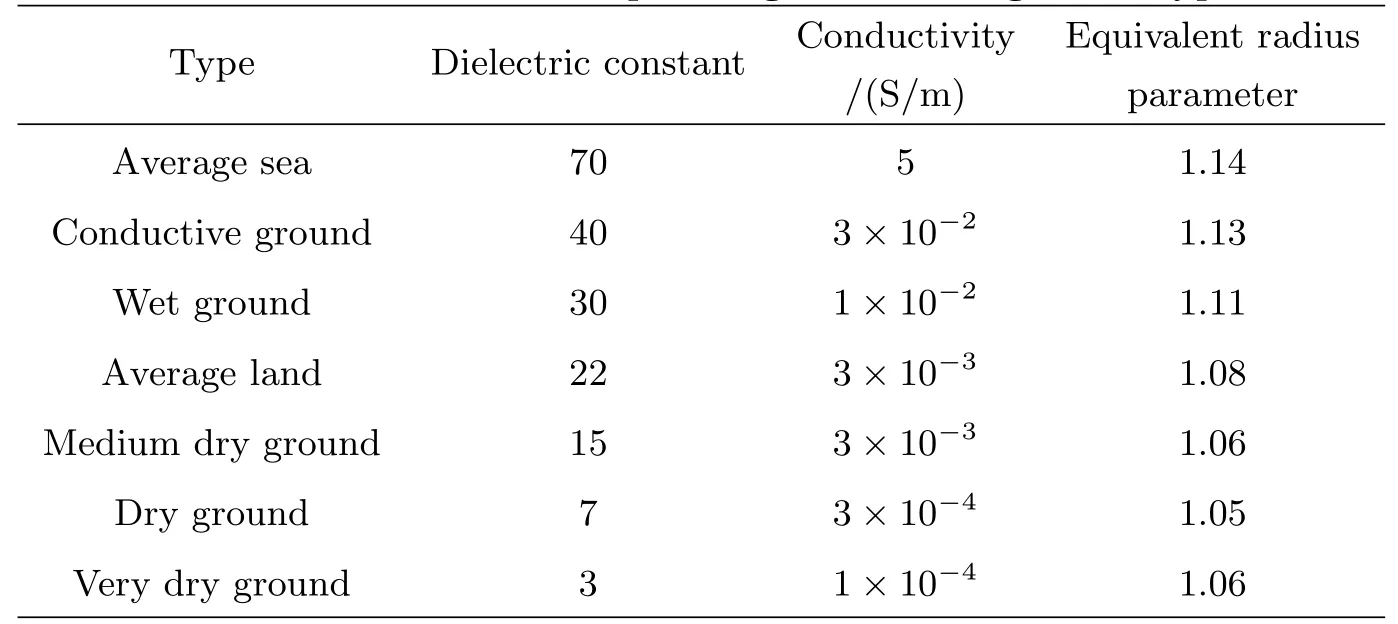
表1 各种地面类型对应的参数[22]Table 1 Parameters corresponding to various ground types[22]

图1 不同地面类型中ts与距离的关系Fig.1 The relation between propagation delay ts and distance in different types of ground

2.2 罗兰信号场强

罗兰的发播天线可以看成是一个简单的振荡电偶极子系统.在接收点,利用天线对罗兰信号进行接收,接收的信号是交变的电磁波信号,其传播必然符合电磁波传播的规律.任意接收点处地波垂直极化电场强度E的计算公式为[22]:

(4)式中,E的单位为µV/m,Rd的单位为km,发射台天线的实际辐射功率P,单位以kW计.为了描述方便,以dB形式表示场强,其形式如(5)式所示:

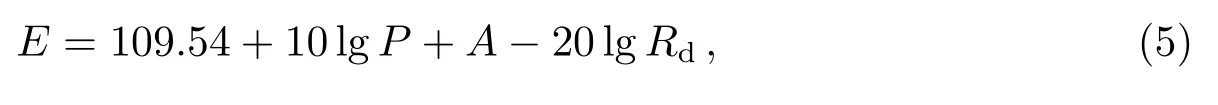
(5)式中,E的单位为dBµV/m,A=20 lg|W|,是以分贝为单位的地波衰减因子.从公式中可以看出,当传播距离和地面类型确定时,地波衰减因子也恒定,实际辐射功率每增加1 kW,接收点的场强增加3 dBµV/m.当天线辐射功率为1 kW时,计算的不同地面类型中场强随地面传播距离的关系如图2所示.从图中可以看出,随着传播距离的增加,各种地面类型中的场强都是逐渐减小.恒定距离上平均海水、良导电地、潮湿地面3种地面类型中的场强差异并不明显.在1000 km的距离上,3种类型中的场强分别为:37.9799 dBµV/m、38.0491 dBµV/m、37.0467 dBµV/m.其他4种类型的结果都小于前面3种,并且地面类型越干燥,传播路径上的衰减越大,接收点场强越小.在1000 km的距离上,甚干燥地中的场强可达−11.9256 dBµV/m,非常不利于罗兰信号的接收.

图2 不同传播介质中的场强随距离的变化趋势Fig.2 The variation of field strength with distance in different propagation media

接收点处罗兰信号场强的大小影响接收机对罗兰信号的接收,根据国际海运事业无线电技术委员会(Radio Technical Commission for Maritime services,RTCM)发布的增强型罗兰接收机最低性能标准要求[23],接收机能够捕获罗兰信号的场强不低于40 dBµV/m.

2.3 定位求解算法

罗兰系统最初采用基于3台2基线的双曲线测时差法进行定位,即在某一位置测量同一台链的两个副台相对于主台的时延差,进而转换为距离差,再利用双曲线定位原理进行定位解算[24].该方法利用时延差消除了罗兰接收机与罗兰系统之间钟差的影响,限制在单台链中求解.近十几年来,罗兰系统大多进行了升级改造,接收机也可以实现伪距的测量[25],出现了利用测量的伪距进行定位授时算法的研究.罗兰系统的伪距定位方程可以表示为:

其中,i是指第i个发播台,i=1,2,3···,ρi为伪距观测值,Rdi表示第i个发播台到接收机的大地线距离.台站位置已知的情况下,大地线距离是用户点2维坐标(φ,λ)的函数.φ和λ分别表示用户点的大地纬度和经度.ts表示传播介质不同于空气造成的传输时间延迟,即二次时延与附加二次时延的和.Tr为接收机本地时钟与罗兰系统的钟差,Pr表示接收系统的时间延迟,即从接收天线接收到信号到接收机输出相应的秒信号为止所经历的接收机处理时延.如果接收系统时延未标校,Tr与Pr可以合并作为一个未知量处理,用Tu表示.否则,Pr的影响可以直接从测量伪距中扣除.不考虑ts影响或者已知ts的情况下,对上面的伪距定位方程在假设的初始位置点P0(φ0,λ0,Tu0)进行局域线性化处理[23]:

该方程组中包含3个未知量,因此至少需要3个伪距方程,以矩阵形式表示:

其中,

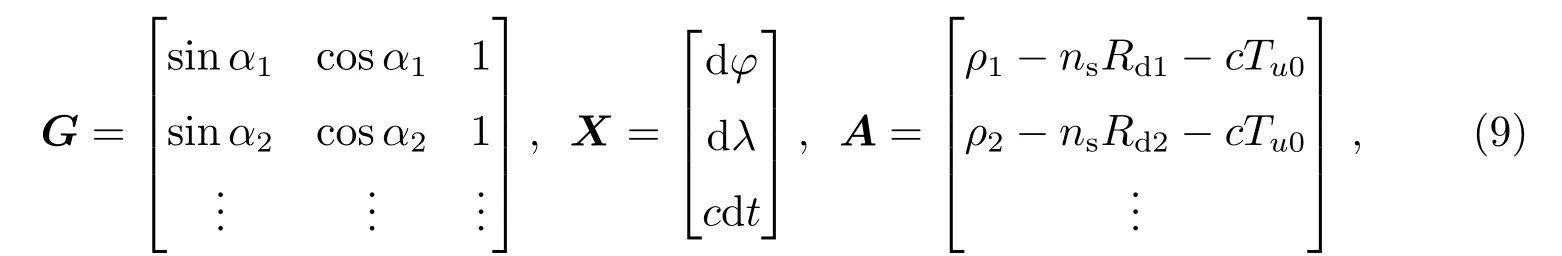
(7)式中αi表示接收点相对于各个发播台站的方位角.Rdi采用Vincenty公式计算.利用最小二乘方法计算:X=(GTG)−1GTA,然后以(φ0+dφ,λ0+dλ,Tu0+dt)更新初始位置点P0,迭代计算,直到X满足设置的阈值为止.罗兰系统的伪距定位求解算法与卫星的伪距定位算法类似,仅在计算Rdi时使用的方法不同.

3 西部台站定位性能

高精度地基授时系统将在我国西部地区新建3个罗兰发播台,其具体位置分别位于库尔勒(Korla)、敦煌(Dunhuang)和那曲(Naqu),结合原有位于蒲城(Pucheng)的长波发播台(呼号为:BPL)以及东部沿海的罗兰台链,实现罗兰信号对我国领域的全面覆盖.将西部罗兰台站用于覆盖区域内的定位,也是罗兰系统发展的必然趋势.罗兰系统的定位误差主要取决于两个因素:首先是伪距的测量误差,其次是用户站与发播台构成的几何精度因子(Geometric Dilution of Precision,GDOP).为了分析西部台站的定位性能,首先需要定性分析西部台站的信号覆盖区域,因为罗兰系统要实现定位,必须要求接收机能够接收到各个台站的发播信号.

通过前面罗兰信号场强部分的描述,罗兰接收机能够顺利接收到罗兰信号要求接收点处的场强应不低于40 dBµV/m.换言之,接收点处场强为40 dBµV/m对应罗兰接收机能够接收到信号的最远距离.假设天线的有效辐射功率为300 kW,分别计算罗兰信号在几种典型地面类型中传播时所对应的最远传播距离,计算结果见表2.从表中可以看出,平均海水所对应的最远传播距离最大,可达1961.371 km,其他几种地面类型中最远传播距离逐渐减小,这主要是由于信号在各种地面类型中的衰减因子不同.我国西部地区主要以沙漠、戈壁、干土为主,是典型的较干燥区域.因此,信号的最远接收距离约为1181.952 km,以该距离为半径,以我国西部新增台站为中心,西部3个台站的信号覆盖区域见图3(a)所示.当罗兰接收机位于3个台站的公共覆盖区域才能同时接收到3个台站的信号完成定位功能.因此,3个台站的公共覆盖部分才是定位区域.随着接收机接收性能的提升,接收的范围也会增加,当接收机能够接收不低于30 dBµV/m的信号时,较干燥地中最远的接收距离为1463.432 km,从而台站的覆盖范围和定位区域都会增加,见图3(b)所示.当接收机能够接收不低于20 dBµV/m的信号时,较干燥地中最大的接收距离为1749.927 km,信号覆盖范围和定位区域会更大.鉴于此,为使台站的定位覆盖区域增加,应进一步提升罗兰接收机的接收性能,使其能够在更低的场强环境中接收信号.

表2 罗兰信号在典型地面类型中对应的最远传播距离Table 2 The longest propagation distance among various ground types

定位误差主要由用户站与发播台站构成的几何精度因子以及用户站的观测误差决定,下面以3个台站的公共覆盖区域为研究对象,从几何精度因子和定位误差两个方面分析3个西部台站的定位性能.

3.1 西部台站GDOP值

用户接收点与发播台构成的GDOP是影响罗兰系统定位性能的一项关键因素[26],反映了发播台站几何布局对伪距观测误差的放大程度.在观测误差恒定的情况下,GDOP值越小,定位误差也越小.我国西部新增台站的位置分别位于库尔勒、敦煌和那曲.从台站的地理位置分析,3个台站的几何结构为三角形,几何布局较均匀.图4给出了西部台站在覆盖区域内的GDOP值,图中仅显示了GDOP小于20的部分,虚线包围的区域为定位区域.从图4中可以看出,3台站的中心区域的GDOP值较小,从中心区域向外,GDOP值逐渐增大.在西部台站的定位区域内,大部分区域的GDOP小于6,与定位区域外的GDOP相比,在定位区域内的GDOP值对观测误差的放大程度较小.

图3 西部台站的覆盖区域以及定位范围.地面类型为较干燥地.左图Rd=1181.952 km,E=40 dBµV/m,右图Rd=1463.432 km,E=30 dBµV/m.Fig.3 Coverage and positioning area of western stations.The ground type is medium dry ground.Left panel Rd=1181.952 km,E=40 dBµV/m,right panel Rd=1463.432 km,E=30 dBµV/m.

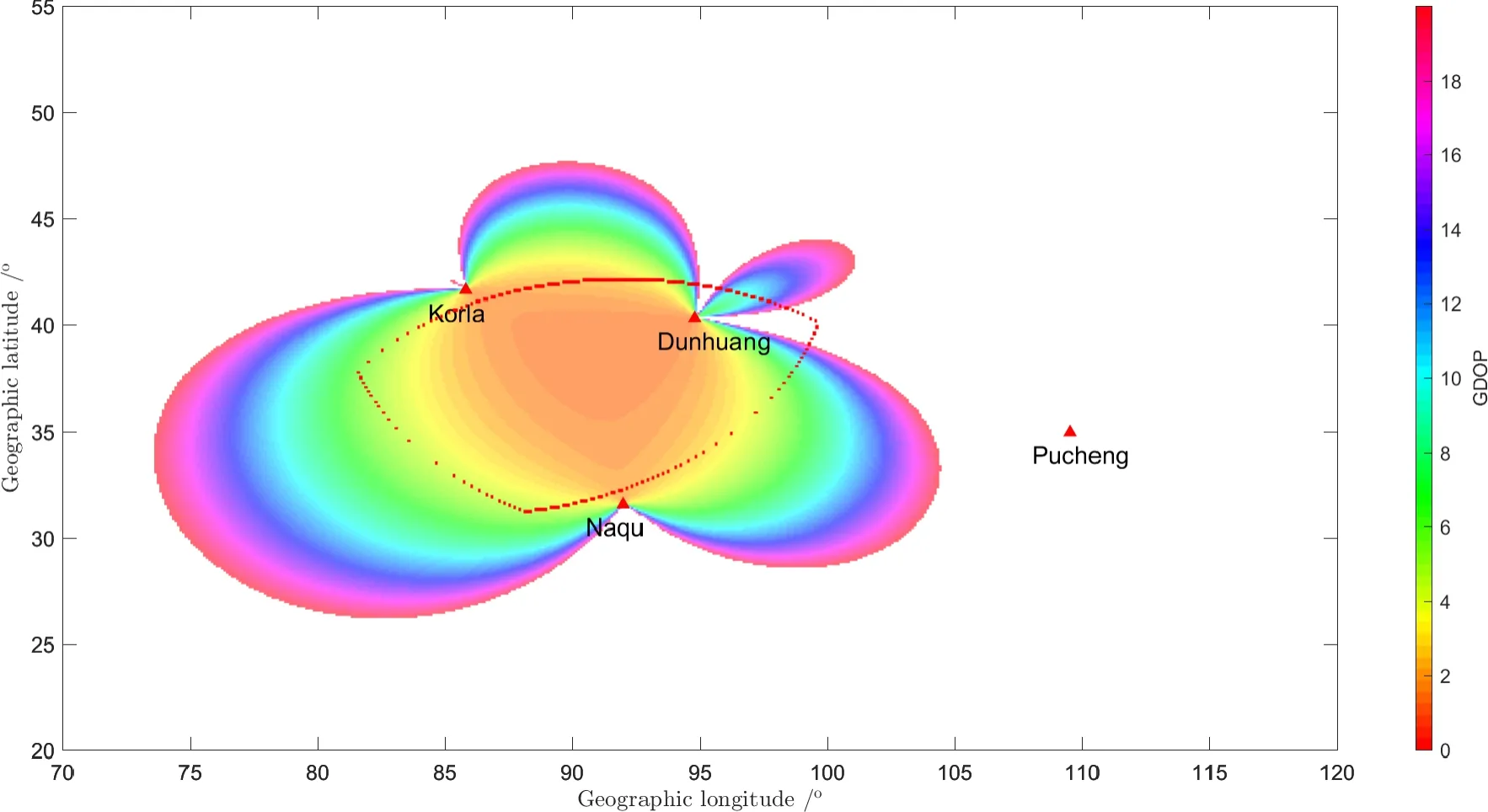
图4 西部台站的几何精度因子Fig.4 The GDOP of western stations

3.2 定位误差

定位误差是几何精度因子和伪距测量误差综合作用的结果.假设西部区域为较干燥区域,仿真计算发播台站到定位区域内任意一点的二次时延和附加二次时延值,用于定位解算,比较定位结果与仿真位置点的定位误差,分析台站的定位性能.为了描述方便,以工作区域内任意选择的3个点A、B、C为例,利用Vincenty公式计算发播台站到3点的距离.同时结合罗兰信号传播时延的公式计算ts,以此构造观测伪距值.接收机钟差在伪距观测值中体现为公共项,这里假设接收机钟差为零.表3给出了3点的仿真数据,其中,ρ为伪距,Lat和Log分别为纬度和经度,坐标值中的N代表北纬,E代表东经.

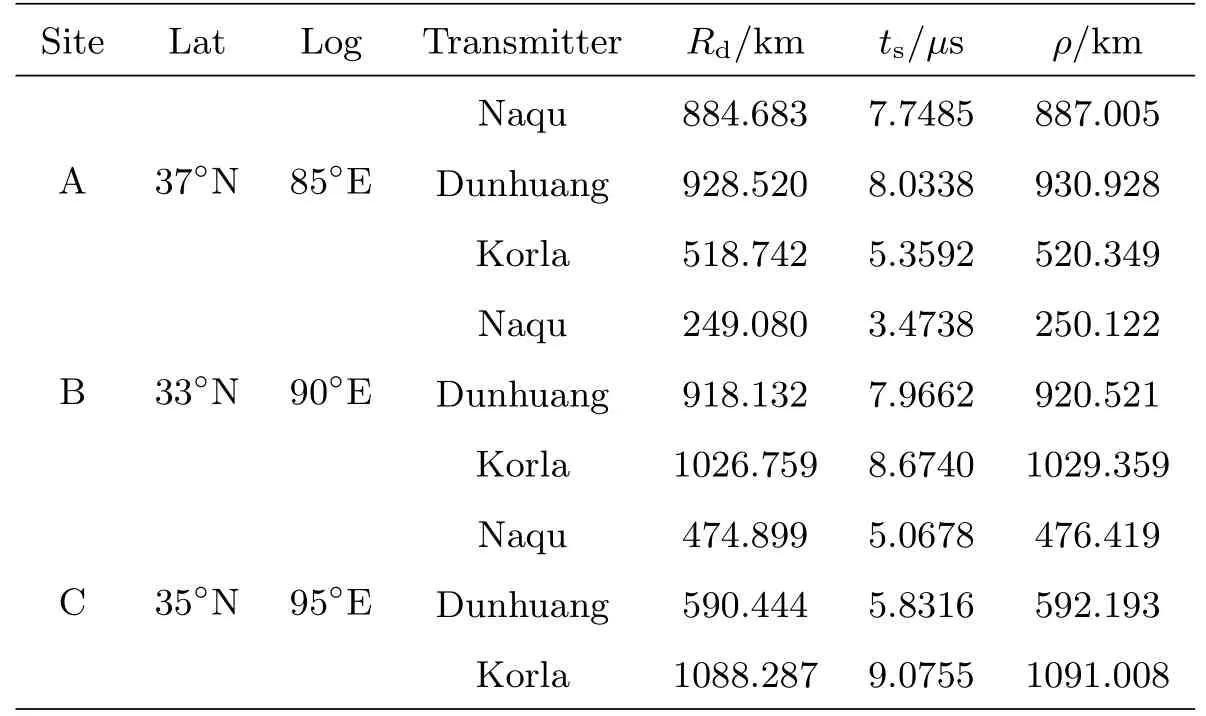
表3 测试点位置及伪距值仿真Table 3 Simulation of test point position and pseudo range

利用2.3节给出的定位求解算法和表3中的伪距值,计算A、B、C 3点的求解位置,数值解算结果分别为:A点(37.0005°N,84.9886°E)、B点(32.9925°N,90.0024°E)、C点(34.9939°N,95.0190°E),与表3给出的真实位置有些许的差异,定位误差表示为求解结果与真实位置的差值.可见,虽然二次时延和附加二次时延相对于基本时延是一个小量,但是依然会造成一定的定位误差.在定位中,纬度或经度方向0.001°的误差近似为108 m.因此,A、B、C 3点在纬度方向的定位误差(纬度误差)分别为:54 m、−810 m、−658 m,在经度方向的定位误差(经度误差)分别为:−1231 m、259 m、2052 m.采用同样的仿真方法计算一定范围内由3个台站解算的纬度和经度方向的定位误差,纬度方向和经度方向的计算结果如图5(a)和图5(b)所示.图中只显示了误差绝对值小于4000 m的部分.从图5(a)中可以看出,当3个台站位置固定时,由3个台站计算的纬度方向定位误差与纬度有关,在纬度37.5°附近,纬度误差的值较小,一般小于200 m,在纬度大于37.5°附近的区域,纬度的定位结果大于真实值,而在纬度小于37.5°附近的区域,纬度定位结果却小于真实值.在敦煌站东边的定位区域,纬度误差大于4000 m,在图形中未显示.该区域纬度误差较大与该区域的GDOP值有关.类似地,从图5(b)的结果看出,经度方向的定位误差与经度值有关,在经度90°附近,经度误差也较小,在经度小于90°的区域,经度的定位结果小于真实值,而在经度大于90°的区域,经度的定位结果大于真实值.同样,敦煌站东边的定位区域,经度误差也大于4000 m.在定位覆盖区域内,以纬度和经度方向定位误差小于10000 m为界,计算定位解算点与真实位置的径向误差.统计结果表明,计算区域内径向误差小于1000 m的点约占总计算量的40.8%,径向误差大于1000 m且小于4000 m的点约占总计算量的53.8%,这两部分占了总量的94.6%,即定位区域内94.6%的径向误差小于4000 m.

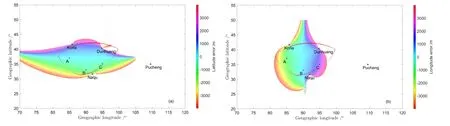
图5 纬度方向(左)和经度方向(右)的定位误差Fig.5 The position error in latitude(left)and longitude(right)directions

4 结论

本文在罗兰信号传播时延预测的基础上分析了不同地面类型中电参数对传播时延的影响以及时延和场强随距离的变化关系.从计算结果可知,地面电参数对传播时延和场强都有影响.在恒定的距离上,相比其他的地面类型,海水引起的二次时延最小.随着传播距离的增加,二次时延也会增加.接收点的场强与天线发播功率、接收点距离发播台的距离以及地面类型等因素有关.随着距离增加,场强大致呈减小趋势.根据罗兰接收机最低性能标准,在满足接收条件的情况下分析了西部台站的覆盖范围和定位区域,然后基于观测伪距给出了椭球面上基于伪距的定位求解算法.在西部台站位置固定的情况下,仿真了定位区域内的几何精度因子,并结合罗兰信号传播特性,计算了西部台站覆盖范围内的定位误差,尤其是伪距中包含二次时延和附加二次时延影响情况下纬度和经度方向的定位误差.结果表明,西部台站的几何布局较为合理,但是由于二次时延和附加二次时延的影响,纬度和经度方向定位误差较大.在台站位置确定的情况下,为提高定位精度,必须采用差分等抑制观测误差的方法削弱二次时延的影响.为扩大罗兰台站定位区域及使用范围,接收机的接收能力有待进一步提升.