姿态卡尔曼滤波对FAST馈源舱BDS/SINS组合导航位姿精度的提高*

李明辉 姜 鹏 于东俊 宋本宁 骆亚波 孙京海

(1中国科学院国家天文台北京100101)

(2中国科学院大学北京100049)

(3长沙理工大学交通运输工程学院长沙410076)

1 引言

目前,500 m球面射电望远镜(The Five-hundred-meter Aperture Spherical radio Telescope,FAST)是世界口径最大且灵敏度最高的单口径射电望远镜(图1).FAST的接收机安装在30吨重的馈源舱底部,馈源舱位置和姿态的测量精度会影响接收机的对准精度.为了提高对馈源舱位置和姿态的导航精度,采用北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)和捷联惯性导航系统(Strap-down Inertial Navigation System,SINS)组合的导航方式.一般情况,将BDS与SINS两者的位置和速度信息分别做差,差值作为卡尔曼滤波算法的量测值,对组合导航系统的状态量进行最优估计[1–2].但随着卫星导航精度的提高,采用多天线技术可以解算出载体的姿态[3–4],将姿态差值也作为量测值,卡尔曼滤波算法的量测值维度就可以由原来的6维扩充到9维,从而提高导航信息状态量最优估计的精度.如果采用传统的BDS多天线定姿算法,用3个姿态角表示空间姿态旋转矩阵,那求解过程需要采用泰勒级数将非线性方程转化成线性方程,解算过程复杂.为了简化姿态求解,本文采用罗格里德矩阵空间坐标转化方法[5–6],规避非线性解算问题,降低空间旋转矩阵求解复杂度.

图1 FAST示意图Fig.1 Illustration of the FAST

2 基于罗格里德矩阵的姿态解算模型

姿态求解是确定一个坐标系相对另一个坐标系的空间转换关系.首先,馈源舱的姿态导航就是确定馈源舱坐标系相对于导航坐标系的转动情况;其次,SINS系统内部进行姿态导航的陀螺是以地心惯性系和地球坐标系为参考系的;再次,FAST望远镜内部设备众多,为了坐标系统一,人为定义了一个FAST坐标系.

2.1 坐标系定义

f-FAST坐标系:对FAST馈源舱的导航是将FAST坐标系作为参考系的,FAST坐标系的原点是望远镜基准球面的球心,xf轴指向地理东向,yf轴指向地理北向,zf轴垂直于当地水平面指向天向;

b-馈源舱坐标系:其原点为馈源舱的重心,yb轴指向馈源舱运动方向,xb轴在水平面内垂直yb轴,zb轴垂直于水平面,3轴遵守右手定则;

e-地球坐标系:原点为地球中心,xe轴和ye轴在地球赤道平面内,其中xe轴指向本初子午线,ze轴为地球自转轴,并指向北极,地球坐标系为右手直角坐标系;

i-地心惯性坐标:原点为地球中心,xi轴和yi轴在地球赤道平面内,其中xi轴指向春分点(赤道面与黄道面的交线再与天球相交的交点之一),春分点是天文测量中确定恒星时的起始点,zi轴为地球自转轴,并指向北极.惯性传感器的输出就是以该坐标系为参考基准的;

n-导航坐标系:原点定义为运载体的重心,xn轴指向地理东向,yn轴指向地理北向,zn轴垂直于当地旋转椭球面指向天向.

BDS多天线方法解算馈源舱姿态时,先要解算b系到f系的旋转矩阵,然后由旋转矩阵求解出航向角ψ,俯仰角θ,横滚角γ.e系、i系、b系和n系用于求解SINS的位置,速度和姿态更新过程.对比f系和n系,可见他们的3轴指向是一样的,只是原点不同,所以可认为f系和n系是平移关系,所以BDS多天线馈源舱姿态解算的等于SINS姿态更新求解的.

2.2 空间姿态旋转矩阵解算

设f系坐标与b系坐标变换关系如(1)式,式中,Xf、Yf、Zf是BDS接收机在FAST坐标系(f系)的坐标,xb、yb、zb是BDS接收机在馈源舱坐标系(b系)的坐标,是空间姿态旋转矩阵,∆Xf、∆Yf、∆Zf是平移量.

(4)式中含有a、b、c和∆Xf、∆Yf、∆Zf6个未知数,但馈源舱上分布3个北斗接收机,可以列9个方程式,按最小二乘拟合原则,当未知数个数小于方程式个数时会引入残差量,(4)式的右边分别引入残差量εx、εy、εz,设残差向量为V.设拟合参数=[a;b;c;d;e;f],其中d=−∆Xf−c∆Yf−b∆Zf,e=c∆Xf−∆Yf−a∆Zf,f=b∆Xf+a∆Yf−∆Zf.设常数项L=[xb−Xf;yb−Yf;zb−Zf],当选用3个北斗天线坐标时,L是9×1的向量.设系数矩阵A1,1号天线的系数矩阵如(5)式,A2和A3分别是2号和3号天线的系数,应用3个天线时,A是9×6的矩阵.

所以(4)式可以改写成矩阵形式,如(7)式:

3 BDS/SINS组合导航

BDS/SINS组合导航可以确定运动物体的空间位置、速度和姿态,单台BDS导航可以确定物体的位置和速度,3台以上BDS共同导航时,还可以确定物体空间姿态,但卫星导航稳定性差,会有如卫星信号丢失、多路径效应等问题.SINS导航是自主导航系统,不受外界干扰,但SINS导航算法是积分过程,初始值误差和系统误差都分别被积累,使得导航结果快速发散.将两者结合使用,可以提高导航的稳定性和精确度.

3.1 天线分布

馈源舱是一个正六边体,在其顶部选择等间隔的3个顶角分别放置北斗天线,天线构型是等边三角形,边长约9 m,天线分布俯视图如图2.

图2 北斗天线在馈源舱的分布示意图Fig.2 Distribution diagram of Beidou’s antenna on the feed cabin

3.2 姿态卡尔曼滤波方程

卡尔曼滤波是一种最优递推滤波方法,是对系统状态的线性最小方差无偏估计.卡尔曼滤波方程包括空间状态方程和量测方程,如(9)式所示,

式中,下标k表示k时刻,k/k−1表示由k−1时刻向k时刻转移.Xk是k时刻的状态向量,Zk是量测向量,ϕk/k−1是状态转移矩阵,Hk是量测矩阵,Γk/k−1是系统噪声分配矩阵,Wk−1、Vk分别是系统噪声向量和量测噪声向量,都是均值为零的高斯白噪声,且系统噪声协方差阵Qk是非负定的,量测噪声协方差阵Rk是正定的.

其中E表示求期望.根据卡尔曼滤波公式[3],状态一步预测为:

状态一步预测均方误差阵为:

滤波增益为:

状态估计为:

状态估计均方误差阵为:

将(12)式代入(13)式中可知,Qk越小,滤波增益Kk越小,(14)式中的对的贡献越大,物理意义是系统噪声越小,系统状态在状态估计(14)式中占的权重越大;而Rk越小,Kk越大,(14)式中的Zk对的贡献越大,即量测噪声越小,测量向量在估计中占的权重越大.所以在滤波时,噪声参数Qk和Rk的选取很重要,对滤波结果影响很大.

状态向量X是15维的,

式中,ϕ是SINS失准角,∆v是SINS速度误差,∆p是SINS位置误差,ε是陀螺器件误差,σ是加速度计器件误差,下标1×3表示矩阵是1行3列.传统卡尔曼滤波中,量测向量Zk一般选取的是卫星导航位置参数与SINS导航位置参数的差值和两者的速度差值.在第1部分,采用北斗多天线方案可以解算出姿态参数,所以在量测向量中增加卫星导航姿态参数与SINS导航姿态参数的差值,这样提高导航精度.姿态卡尔曼滤波中,量测向量Zk的形式如下:

式中下标B表示北斗导航数据,S表示SINS导航数据,次下标E、N、U分别表示东向、北向、天向,v、L、λ和h分别是速度、纬度、经度和高度.

4 实验数据分析

实验数据为2020年9月16日北京时间14:11–14:15期间望远镜为跟踪观测模式时,BDS接收机和SINS内加速度计、光纤陀螺的实时数据.将两者数据用于组合导航解算,求解出馈源舱实时姿态和位置,然后与理论规划数据进行对比,获得Rmse(Root Mean Squared Error)值.组合导航中,采用两种滤波方法,方法1是量测向量Zk只包括BDS和SINS的速度差值和位置差值的传统滤波;方法2是姿态Kalman滤波,量测向量Zk如(17)式所示,增加了两者的姿态差值.两种方法的对比结果如图3–8所示,其中图3–5显示的是两种滤波方法下馈源舱的实际导航姿态与理论规划姿态的误差值,图3是姿态中横滚角的误差值,图4是姿态中俯仰角的误差值,图5是姿态中航向角的误差值;图6–8显示的是两种滤波方法下馈源舱的实际导航位置与理论规划位置的误差值,图6–8分别是xf、yf、zf轴位置的误差值.图中的红线表示姿态滤波方法的导航结果与理论规划数据的误差值,蓝线表示传统滤波方法的导航结果与理论规划数据的误差值.图例的avp中a表示BDS与SINS的姿态(attitude)差值,v表示BDS与SINS的速度(velocity)差值,p表示BDS与SINS的位置(position)差值.

图3 两种滤波方式的横滚角误差值对比图Fig.3 Error value of roll angle with different filters

图3中红线表示姿态滤波方法解算下,馈源舱实际横滚角与理论横滚角的误差值,蓝线是传统滤波方法下,实际与理论俯仰角的误差值.两种滤波方法的误差值稳定性情况相似,误差数据波动幅值也相似,但姿态滤波方法的误差均值的绝对值小于传统滤波方法,表明姿态滤波方法的横滚角精度更高.图4是俯仰角误差对比图,结论与图3相似.

图5是航向角误差对比图,在组合导航中航向角的最优估计是最难的,因为航向角不准确所引起的误差量级远小于俯仰角和横滚角引起的误差量级,所以在滤波中容易被视为系统误差而滤除,导致航向角很难通过传统滤波方法进行优化.从图中可以看出姿态滤波方法的误差值区间明显更小且均值更小,姿态滤波的航向角误差均值是0.020°,传统滤波的航向角误差均值是0.028°.在均方根误差值上,姿态滤波的优势更明显,Rmse值由传统滤波的0.0035°,下降到0.0017°,表明姿态滤波可以使航向角精度稳定性提高一倍.

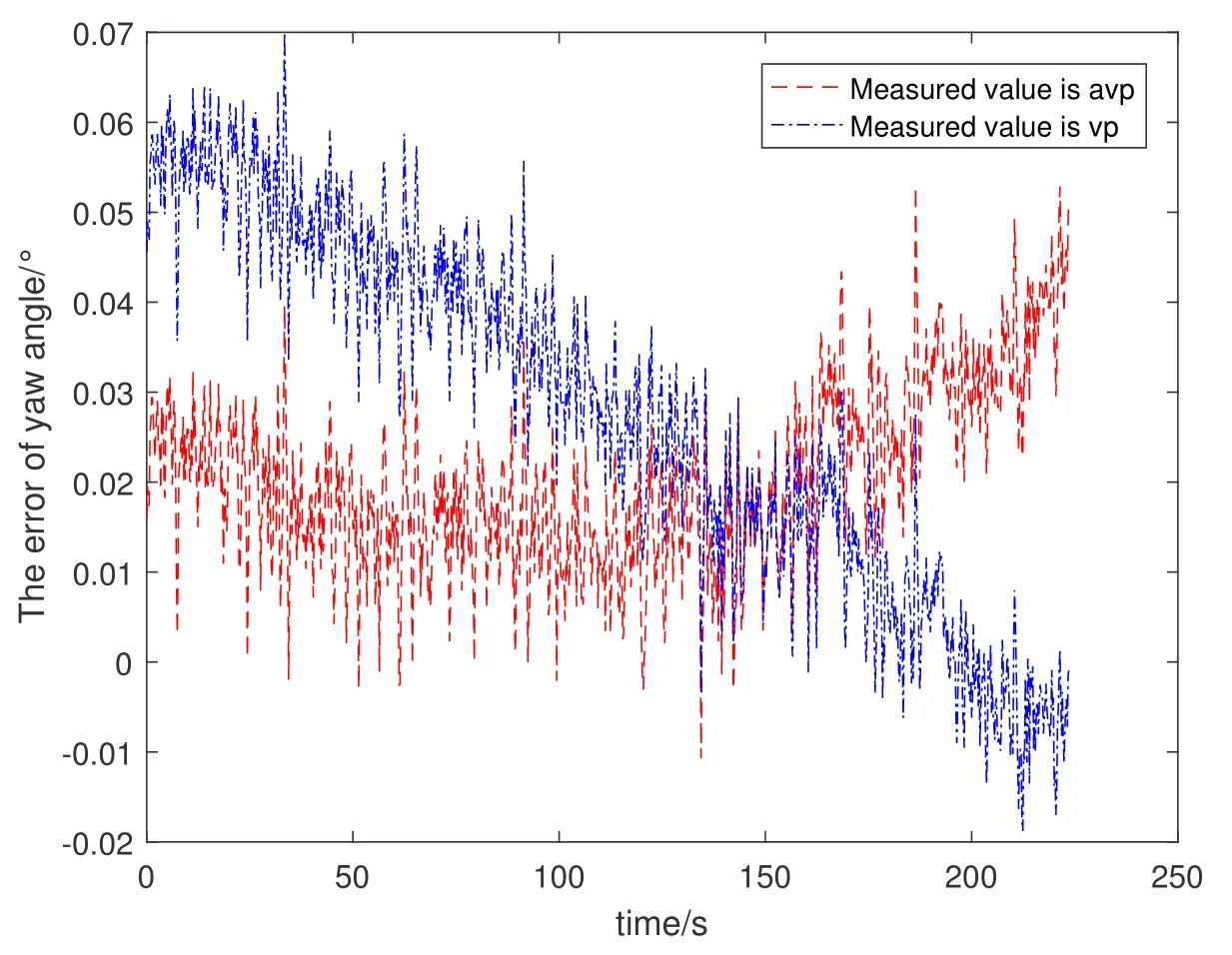
图5 两种滤波方式的航向角误差值对比图Fig.5 Error value of yaw angle with different filters

图6 两种滤波方式在xf轴位置误差对比图Fig.6 Error value of position in xf axis with different filters

图7 两种滤波方式在yf轴位置误差对比图Fig.7 Error value of position in yf axis with different filters

图6–8是两种滤波方法下,导航位置与理论规划位置的误差对比.从图6可见,姿态滤波可以使xf轴位置精度有所提高.从图8可见,在zf轴位置上,姿态滤波与传统滤波效果基本相同.从图7可以看出姿态滤波对yf轴位置的精度提高明显,姿态滤波的yf轴位置的误差均方根是0.00638 m,传统滤波的yf轴位置的误差均方根是0.00736 m,表明姿态滤波可以使yf轴位置精度提高.

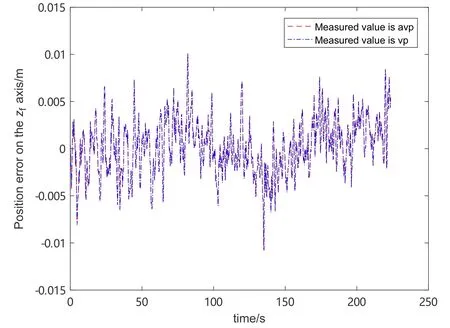
图8 两种滤波方式在zf轴位置误差对比图Fig.8 Error value of position in zf axis with different filters

5 结论

采用两种滤波方法,对获得的组合导航结果进行分析,将位置和姿态的Rmse值列入表1中.从表1可见,在传统卡尔曼滤波的测量向量Zk中增加姿态差值后,馈源舱组合导航结果的精度有提高,尤其对于导航中最不容易进行最优估计的航向角,姿态滤波可以使航向角的精度提高一倍.此外,yf轴位置精度提高了13%,但增加了姿态差值的同时,也增加了量测噪声协方差阵Rk的维度,增加了滤波器参数调节的工作量.

表1 两种滤波方法的馈源舱组合导航结果Rmse值Table 1 The Rmse of the integrated navigation results with the difference filtering methods