基于小波变换的射频干扰消除方法的研究*

林天琪 吴亚军 朱人杰 徐志骏

(1中国科学院上海天文台上海200030)

(2中国科学院大学北京100049)

(3中国科学院射电天文重点实验室南京210023)

1 引言

近年来射电天文快速发展,一方面,国内上海天马65 m射电望远镜、500 m口径球面射电望远镜(FAST)相继投入运行,新疆奇台110 m射电望远镜、云南景东120 m脉冲星射电望远镜等正在预研.另一方面,国际上平方公里阵(SKA)项目开始建造,其他大量的望远镜投入使用和升级,如:阿塔卡马大型毫米波/亚毫米波阵列(Atacama Large Millimeter/Submillimeter Array,ALMA)、下一代的甚大天线阵(Next-Generation VLA,ngVLA)、国际低频阵列(Low-Frequency Array,LOFAR)、默奇森宽场阵列(Murchinson Widefield Array,MWA)、加拿大CHIME(Canadian Hydrogen Intensity Mapping Experiment)天文望远镜等.与此同时超宽带致冷接收系统的研究也取得进展,这些技术将射电观测的灵敏度推向前所未有的高度,在此背景下射频干扰(RFI)成为一个日益突出的问题.

对RFI缓解技术的方法可分为3类[1]:第1类是防止RFI信号进入天文数据.在《无线电规则》和《中华人民共和国无线电频率划分规定》文件中,都通过对频段和发射功率的相应要求来保护射电天文业务.在望远镜选址工作中,也会尽可能挑选远离人类活动的区域,并建立无线电宁静区域[2].第2类是实时去除数据中的RFI信号.实时去除RFI信号,可以在数据接收后对数据进行基于软件和硬件的实时处理操作.WSRT(Westerbork Synthesis Radio Telescope)利用FPGA(Field Programmable Gate Array)执行初始频域滤波,然后利用累积求和对接收到的数据进行阈值处理[3].在相控阵中利用辅助天线、自适应调零等方法也可以很好地消除RFI信号[4].第3类是在相关和数据集成或数据缓冲之后去除RFI.现今对射频干扰后相关消除的技术繁多,文献[5–6]提出了利用形态运算符、SumThreshold方法、背景拟合技术相结合,组合成一个通用方法来处理RFI信号.该方法成功地用于几个干涉望远镜,包括LOFAR、WSRT、VLA(Very Large Array)、GMRT(Giant Metrewave Radio Telescope)、ATCA(Australia Telescope Compact Array)、Arecibo、MWA以及单碟望远镜Parkes.文献[7–9]中提出了一种基于谱峰度的RFI提取算法,通过判断数据的谱峰度(SK)来识别RFI信号并标记.该算法利用得到的SK估计值的期望统计方差,定义了RFI检测的阈值.

上述几种方法能够很好地根据数据特性对数据是否有干扰进行标记,但不能实现数据干扰的消减.而在文献[10]中利用了独立成分分析法来消除射频干扰信号,将射频干扰信号从信号中分离.独立成分分析能够很好地消除干扰信号,但需要多通道的数据进行分析.本文提出了基于2维小波变换的方法标记和消除射频干扰,对信号中存在的干扰进行标记,并能够将信号中的射频干扰信号去除.将数据的时间频率序列作为原始数据,用小波变换中的系数作为干扰存在的判据对数据进行标记,利用绝对中位差作为阈值将干扰信号分辨出来,通过改变变换后的小波系数对数据进行处理.实验证明,该方法提高了数据的信噪比,能够很好地标记干扰信号并进行消除.

2 理论基础

2.1 射频干扰信号分析

对于接收到的天文信号,可以建立一个这样的模型:

其中S(n)为所需的天文信号,W(n)是系统接受的噪声信号,I(n)为RFI信号.对于接受到的信号X(n),n为采样序号.在没有经过处理前,所需的天文信号会淹没在噪声信号中,对于RFI信号的消除可以提高信噪比,使得天文信号在后续的处理中受到RFI信号的影响更小.

射电望远镜接收信号时可能会接收到发生在局部频率范围内,但在时间上具有连续性的信号,这类信号就是窄带RFI.移动通信、GPS卫星导航、电视广播等都属于窄带RFI,其数学表达式为:

其中INB为窄带RFI信号,j是虚数单位,A、f、θ分别为干扰信号的幅值、频率和相位,这类信号在经过傅里叶变换之后能够清楚地分辨出来.在数据接收的过程中也会接收到一些宽带的干扰信号.其中存在由于雷击、电子设备短路等情况造成的瞬时宽带RFI,也有输电电缆、以太网电缆等持续的宽带RFI信号.其数学表示为:

其中,式中IBB为宽带RFI信号,Al、fl、θl分别为第l个干扰分量的幅值、频率和相位,L为RFI源的个数.

在实际的观测中,望远镜接收到的信号可以用时间频率序列来表示,RFI信号在图像中也能够很好地辨别出来.有短时间发生突变的较小干扰信号,也有贯穿整个图像的宽带持续信号.图1(a)中竖线为宽带脉冲RFI信号,横线为窄带RFI信号,图1(b)中也存在宽带持续时间信号,RFI往往并不是单一形式存在的,天文观测中存在着复杂的电磁环境,RFI信号交叠存在,使得去除信号更为复杂.

图1 宽带及窄带RFI信号的时间频率序列.图(a)中横线为窄带RFI信号,竖线为宽带脉冲RFI信号,图(b)是宽带持续RFI信号.Fig.1 Time-frequency sequence of wideband and narrowband RFI signals.The horizontal line in panel(a)is the narrowband RFI signal,the vertical line in panel(a)is the broadband pulsed RFI signal,and panel(b)is the broadband continuous RFI signal.

2.2 2维离散小波变换

在处理时间频率序列时,可以将其看作是一个2维图像进行处理.由于小波变换能够覆盖整个频域并且具有变焦特性,通过选择合适的滤波器可以极大减小不同特征间的相关性,在不同频段中可以利用不同的窗口对数据进行处理.在文献[11]中,也利用了一维小波变换进行RFI信号消除.小波变换在图像处理中得到了广泛的应用,因此选用2维离散小波变换对时间频率图像进行处理.

小波变换是一种信号的时间-尺度分析方法,是近代信号分析和处理的一种重要手段.小波变换在时频两域都具有表征信号局部特征的能力,是一种窗口大小固定不变但形状、时间窗和频率窗都可以改变的时频局部分析方法.通过小波变换,对信号进行多尺度的细化分析,能够有效地从信号中提取信息.

由于数据为2维信号f(x,y),因此采用2维离散小波变换对信号进行分解.2维离散小波变换需要一个2维尺度函数和3个2维小波ψH(x,y)、ψV(x,y)、ψD(x,y).ψH(x,y)、ψV(x,y)、ψD(x,y)分别表示信号沿行(H)、列(V)和对角线(D)方向的变化[12–13].

对于给定的尺度函数φr,p,q(x,y)和平移基函数(x,y):

其中,r为尺度参数,p、q分别为沿着x、y方向上的平移参数.对于像素为P×Q大小的图像,经过小波变换分解后的低频系数为:

其中,wφ(r0,p,q)为分解后的低频系数,r0是分解后第0层的系数.经过小波变换分解后的高频系数为:

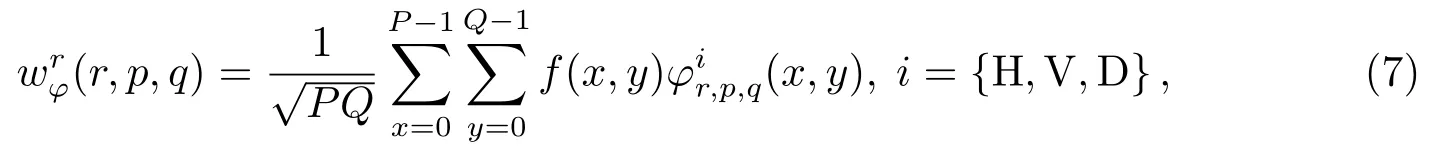
2.3 RFI信号在小波系数中的体现

将数据进行小波变换后,可以得到低频和高频的小波系数,由于RFI存在的形式多种多样,在系数中体现也不尽相同.

对于持续宽带RFI信号,经过小波变换后RFI能量会更多地体现在小波变换的低频部分.在图像中加入高斯信号作为原始信号,再加入一定宽度的信号作为宽带RFI信号.经过小波变换,得到分解后的低频和高频系数如图2所示.由于宽带信号分布映射到时间频率序列图像中占用的面积较大,所以信号分解的小波系数能量会集中在信号的低频部分,但是在加入的信号边缘处,也会在小波分解后的高频系数中存在.

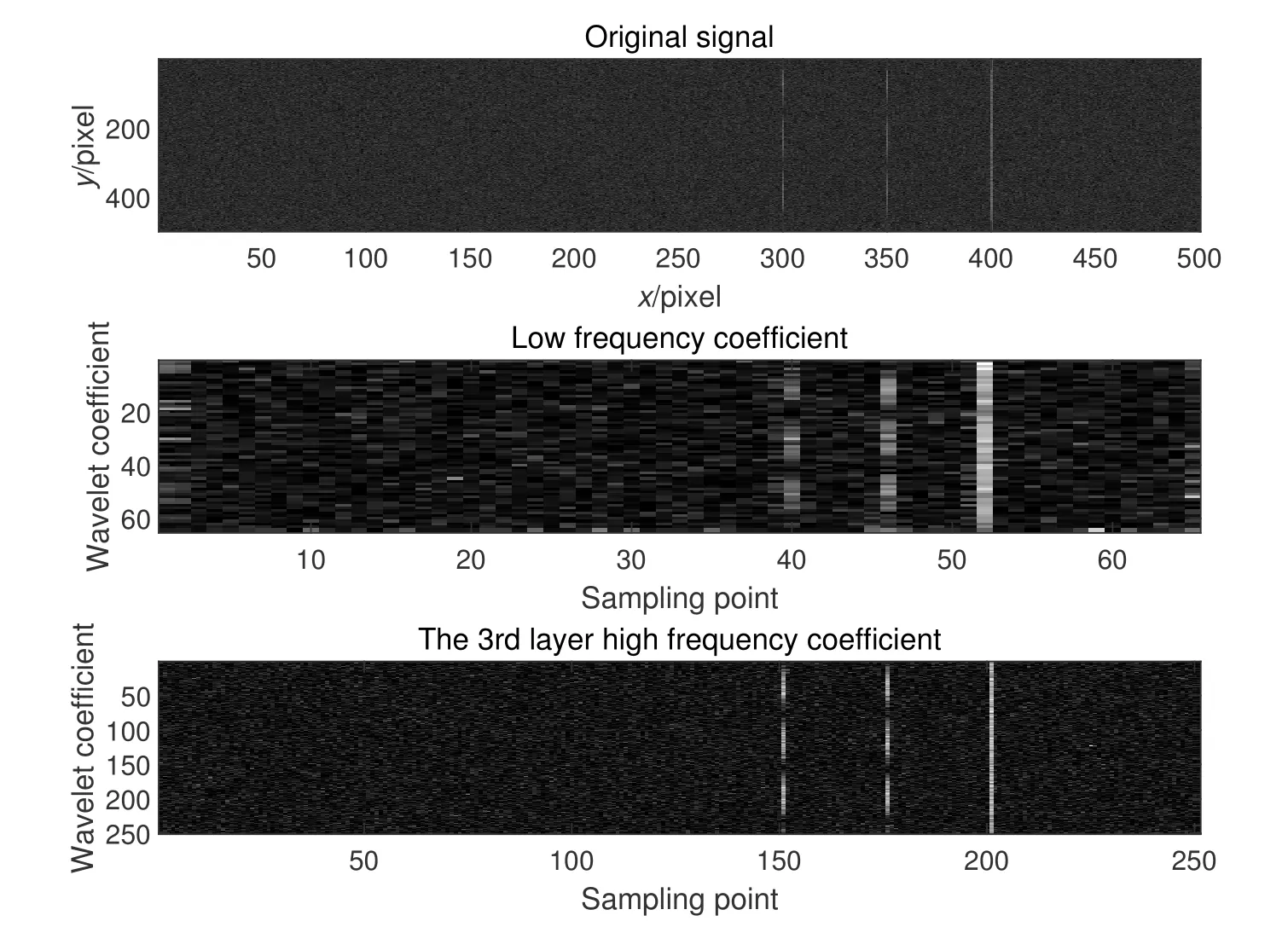
图2 窄带RFI在小波变换中的体现.上图为原始信号,中图为小波分解后的低频信号,下图为小波分解后的第3层高频信号.Fig.2 The embodiment of narrowband RFI in wavelet transform.The top panel is the original signal,the middle panel is the low frequency signal after wavelet decomposition,and the bottom panel is the third layer of high frequency signal after wavelet decomposition.

而对于RFI信号中的宽带脉冲信号、窄带信号以及只有一个突变值的点频瞬时信号,在时间频率序列中往往表现为一条直线和一个很亮的点.它们的信号不一定会出现在低频信号中,但会因为具有突变性而在高频系数中得以体现.

在高斯图像中加入窄带信号和带有突变值的点信号,经过小波变换后得到低频和高频系数,如图3所示.当窄带信号较强时,信号也可以在低频系数中有所体现,但对于信号较弱或者不连续时,会在高频系数中体现得更加明显.

本文采用绝对中值滤波的方式对于小波变换后的系数进行处理.由于天文信号大多淹没在高斯噪声中,所以可以近似看成高斯信号,绝对中位差(Median absolute deviation,MAD)作为检测单变量样本中样本差异性的稳健度量,相较于利用均值和标准差,MAD能够更好地判别出信号中的异常值,可以大大减少其对于数据集的影响.在文献[14–15]中,也利用了MAD方法对RFI信号进行去除.对于给定的信号X(x1,x2,···,xK),其中K为样本个数,其MAD值如下:

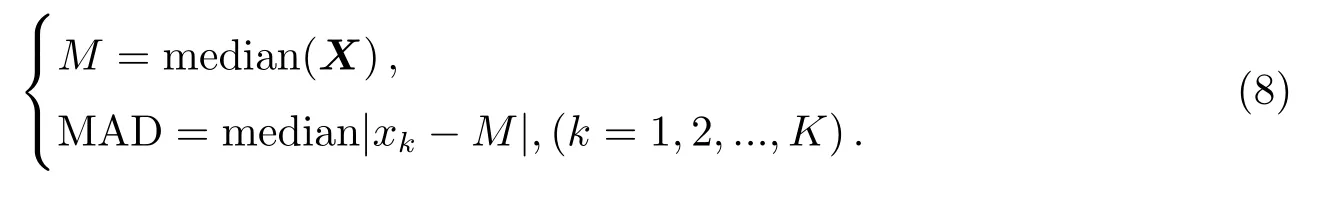
当分布为正态分布时,使用σr=1.4826×MAD作标准差σ的一致估计量.相较于样本差和方差更不容易受到异常值的影响.

3 数据处理分析

3.1 RFI信号标记

由于干扰信号在低频中大多能够体现出来,对于RFI信号的标记,我们利用小波变换得到的低频系数做阈值处理.为了确保标记的精度,应尽量选择较小的小波阈值层数,将小波基函数与信号值进行卷积,通过处理标记低频系数的阈值来标记RFI信号.

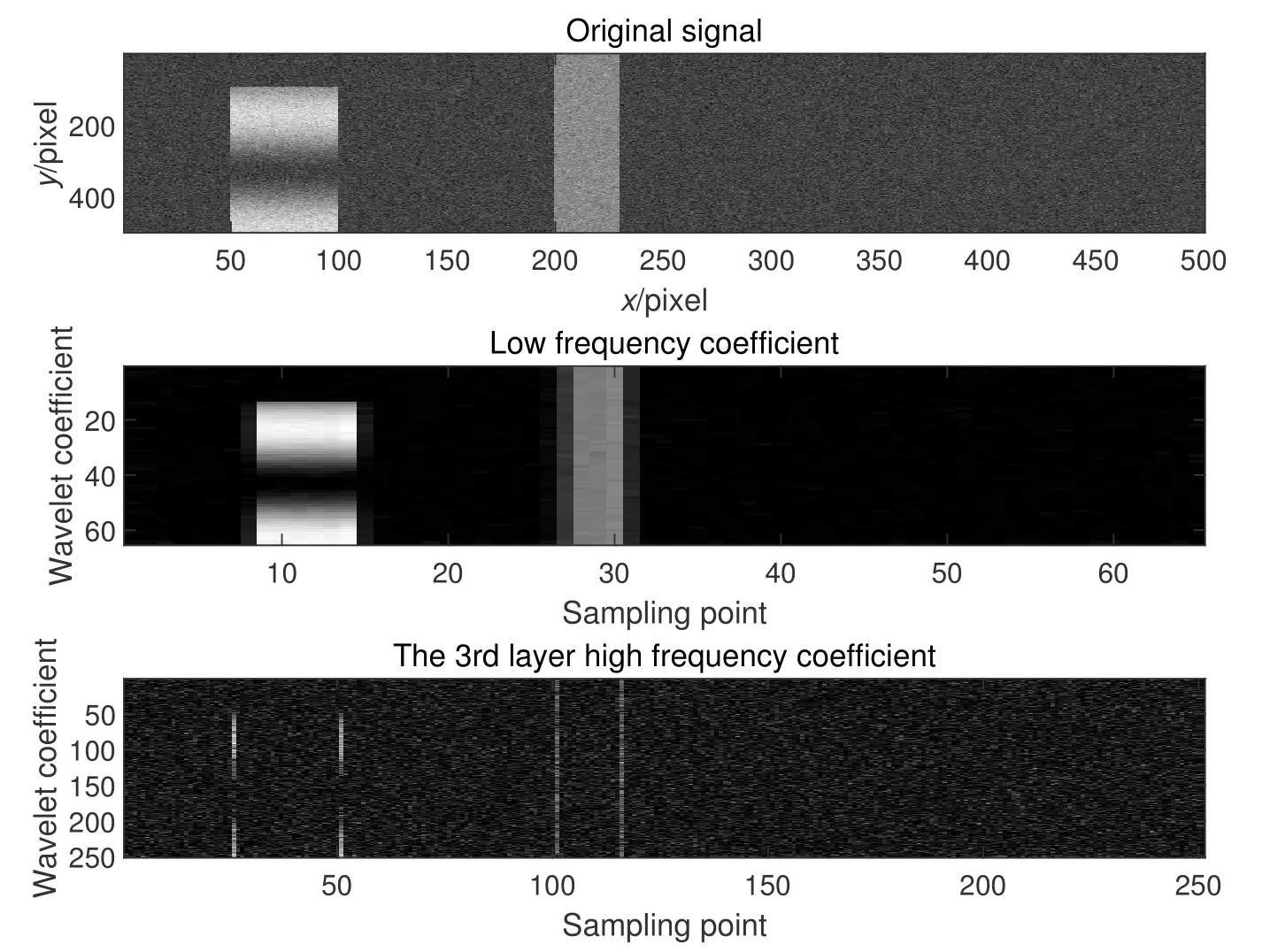
图3 宽带RFI在小波变换中的体现.上图为原始信号,中图为小波分解后的低频信号,下图为小波分解后的第3层高频信号.Fig.3 The embodiment of broadband RFI in wavelet transform.The top panel is the original signal,the middle panel is the low frequency signal after wavelet decomposition,and the bottom panel is the third layer of high frequency signal after wavelet decomposition.

利用时间频率序列作为信号原始图像,对信号进行处理得到小波系数.若原始数据波动较大,可以先对数据做平滑滤波.处理后的数据如图4所示,图中的横线为计算得到的阈值.从图中能够明显看到有干扰的部分模值相对较大,其中超过阈值的部分将被标注出来.数据标注后,将小波系数还原,选择处理前后变化值较大的数据进行标记.

快速射电暴(FRB)是一种高能量、持续时间为毫秒的无线电脉冲.不考虑传播中的闪烁和散射,FRB是一个持续时间短的宽带结构,与脉冲星中观察到的单脉冲类似,当FRB穿过电离层时,信号会产生与频率相关的时延,传播信号的长波比短波要慢上许多,经过消色散的处理之后,可以通过不同频率上数据的叠加来识别FRB的存在.RFI也会干扰FRB的识别.图5是一个带有RFI的FRB数据,数据有336个通道,观测波段为1120–1465 MHz,采样间隔为0.0012 s.对数据进行标记后,通过填充随机数的方式,对标记的干扰信号进行处理,得到进行数据标记处理和消除色散后的结果.图中可以看出信噪比由标记之前的5.06变为8.60.

图4 时间频率序列及其系数阈值处理.上图为原始信号,下图为小波低频系数与阈值的比较图,图中横线为阈值.Fig.4 Time-frequency sequence and its coefficient threshold processing.The top panel is the original signal,the bottom panel is the comparison diagram of wavelet low-frequency coefficients and the threshold,and the horizontal line in the figure is the threshold.

3.2 RFI信号去除

在将信号图像进行2维小波变换后,干扰信号具有更大的模值.在进行RFI信号去除的工作中,期望能在原始数据尽可能不变的情况下更好地消除RFI干扰信号.为了尽量保留更多的原始数据,对于低频系数,先将得到的超出阈值的系数进行低通滤波,再与原始系数相减,使得更多的信号被留存下来.

干扰信号的去除过程如图6所示,具体的操作步骤如下:

(1)对要处理的信号图像进行多层小波变换后,得到各层的小波系数;

(2)对于低频系数,需要对得到的小波系数进行低通滤波,去除有干扰的信号,留下变化较大的信号.图7为系数处理的过程,其中标记为蓝色的线为小波分解后的系数,红色的线为滤波后的信号,黄色的线是小波系数与滤波后结果的差值;

(3)将处理后的小波系数进行阈值处理,选择MAD阈值λ,将高于阈值的系数置零,得到估计的小波系数;

(4)处理后的小波系数重构,得到去除干扰信号的图像.

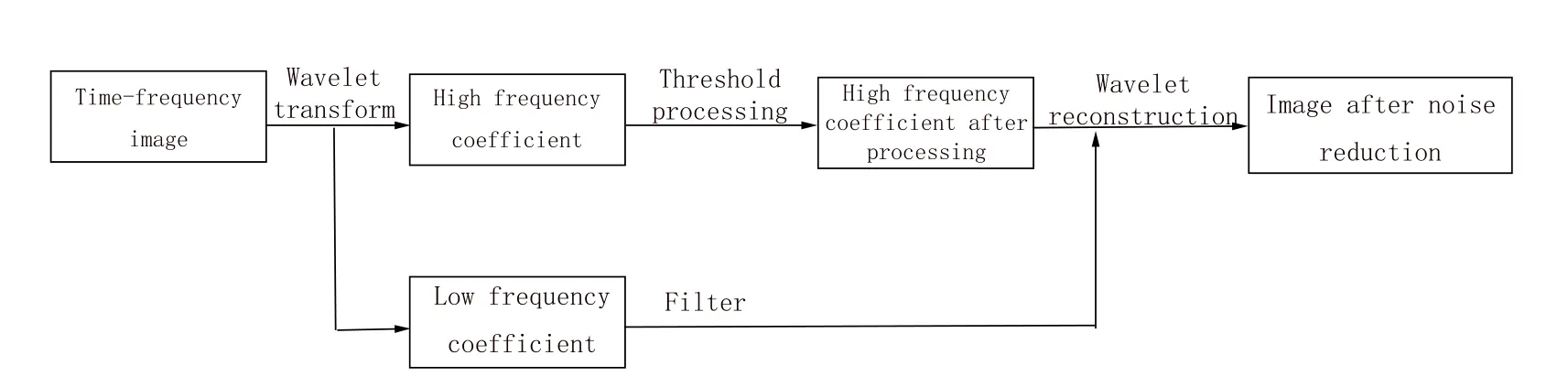
图6 RFI信号去除过程Fig.6 RFI signal removal process

图7 小波系数处理.蓝色为原始信号,红色为滤波后的信号,黄色为最终结果.Fig.7 Wavelet coefficient processing.Blue is the original signal,red is the filtered signal,and yellow is the final result.

在去除时间频率序列的RFI信号时,首先对数据进行小波变换,将标记的低频系数进行平滑处理.然后对标记的高频系数进行阈值处理,最后将信号进行还原.还原信号的结果如图8.图8是一个同时带有FRB信号和噪声信号的数据,数据有221个通道,观测波段为2189.5–2300 MHz,采样间隔为0.002 s.可以看到经过处理后噪声数据被消减,并且保留了FRB信号,信噪比从7.56变为9.11.

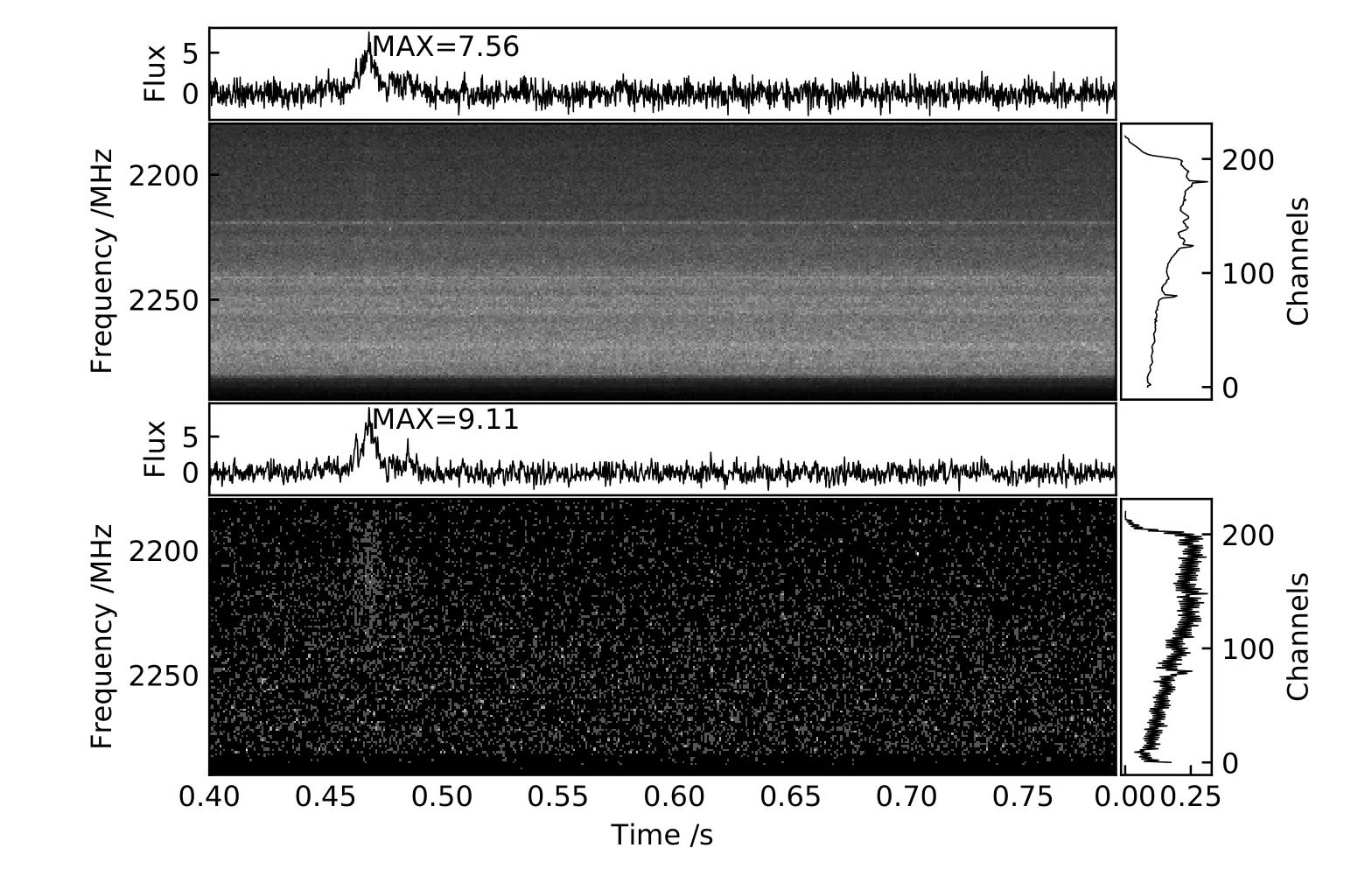
图8 RFI信号去除结果.上图是处理前的图像,下图是处理后的图像,MAX为数据的最高信噪比.Fig.8 The result of RFI signal removal.The top panel is the image before processing,the bottom panel is the image after processing,and MAX is the maximum signal-to-noise ratio of the data.

4 总结与展望

本文提出了用小波变换来标记和去除时间频率序列中的干扰信号,数据通过小波变换之后,利用低频系数标记出干扰信号,并对小波系数中的高低频系数分别处理,利用绝对中位差作为阈值来消除干扰信号.通过对仿真数据和实际观测的数据进行测试,证实该方法能够提高数据的信噪比.由于在信号判别过程中使用的是小波变换的低频系数,如果分解的层数过多,很有可能会扩大数据的标记范围.而对于一些强度不高的信号点,有可能未被标记出来.在干扰数据与信号数据重叠的时候,进行随机数据替换可能降低信号的信噪比.射频干扰信号纷繁复杂,利用阈值处理的结果仍然会有误判和少判的情况存在,后续可以继续优化阈值处理方法,如利用系数间相关性去除干扰信号.