社会模拟算法优化的随机共振轴承故障诊断研究∗

余满华，姜 宏，章翔峰，李晓巍

(新疆大学 机械工程学院，新疆 乌鲁木齐830047)

0 引言

随机共振因其能将噪声能量转化为微弱特征信号能量，从而增强微弱信号的特点，被学者们广泛用于处理强噪背景下的微弱故障信号[1,2]．然而，随机共振由于绝热近似理论，限制了其在实际工程中的应用．二次采样随机共振[3]、参数归一化随机共振[4]、调制随机共振[5]、移频变尺度随机共振[6]和基于频率信息交换的随机共振[7]等扩大了其工程应用．Liu等[8]分析了频率信息交换过程中两次傅立叶变换存在能量泄露的可能性，从而提出在时域上的频率交换，进一步提高精度和扩大了随机共振的工程应用．

轴承作为旋转机械的关键零部件，随机共振也被用于轴承微弱故障诊断研究[9]．滚动轴承局部损伤对振动信号具有调制作用，而包络解调信号可有效地反映此类故障类型[10]．但包络信号是非零均值的非对称信号，若使用双稳态随机共振对包络信号进行处理时，包络信号会越过中介势垒进入负半区势阱，从而引入无意义的频率成分．对此，冯毅等[11]提出了将包络信号作为多稳态随机共振模型系统的输入，实现轴承滚动体微弱故障的诊断．

随机共振系统参数严重影响输出结果，为了自适应的优化系统的参数，张仲海等[12]利用粒子群算法优化随机共振系统参数．还有采用果蝇优化算法[13]、鲸鱼优化算法[14]、人工鱼群算法[15]等启发式优化算法自适应选取系统参数，但存在收敛速度慢且易陷入局部最优等问题．Balochian Saeed等[16]发现了社会民众向社会或行业领军人才学习的现象，研究其规律并建立数学模型，提出了全局收敛速度快、预先设定参数更少的社会模拟优化算法，并用于悬臂梁和压力容器等工程设计方面．

综上分析，本文提出了一种社会模拟算法优化多稳态随机共振的轴承故障诊断方法，将高频特征信号的包络信号变换到低频区，以信噪比为优化自适应函数，利用社会模拟优化算法获得最佳系统参数，从而实现轴承微弱故障诊断．

1 基本理论

1.1 多稳态随机共振

随机共振现象是由非线性系统、微弱特征信号和噪声共同协作产生．本文中非线性系统是过阻尼系统，其方程表达式为[11]：

式中：U(x)为势函数，s(t)为微弱故障特征信号，n(t)为噪声．

文献[17]提出了可以处理非对称信号的多稳态势函数模型，如图1所示，具有3个势阱和2个势垒，其势函数表达式为：

图1 多稳态势函数模型Fig 1 Multi-stable potential function model

式中：参数a和b为正实数，c为实数．

1.2 社会模拟优化算法

Balochian Saeed等[16]发现社会民众模仿和学习

领军人才行为的现象，受此启发，首次提出社会模拟优化算法．在这个优化算法中，“follower”代表个体方案，“leader”代表每次迭代最优方案的适应度值，其详细步骤如下．

（1）初始化

首先，初始化最大迭代次数K、“follower”的人群个数Pop和被优化变量的个数N，初始化第i个方案“follower”的所有变量如式（3）.

lb和ub表示第j个变量的下限和上限，rand表示服从(0，1)正态分布的一个随机数．

其次，利用目标优化函数初始化每个方案的适应度值；

最后，将最大适应度值的方案“follower”定为“leader”方案，其值等于leader．

（2）模仿

首先，计算每个“follower”与“leader”之间的差距“difference”；

如果difference=0，则令difference=rand；

其次，更新每个“follower”中的变量；

最后，更新最优的“follower”方案和leader值；

（3）终止条件

本文选择的终止条件是：判断是否超过预先设置的最大迭代次数，如果没有，则返回步骤（2），反之，结束优化过程，获取最优方案．

2 基于社会模拟算法的随机共振轴承故障诊断

对于故障轴承振动信号存在的调制特性，采用Hilbert变换解调，获得包含故障特征频率信号的包络信号．对于高频率的实测信号，本文采用频率交换[8]和变尺度将高频信号变换至低频，以满足随机共振的条件．随机共振的效果评价指标一般采用输出信噪比，见（6）式，其达到最大值时，非线性系统、微弱低频信号和噪声三者处于最佳的匹配状态．

式中：w表示信号频率，S(w)表示信号能量，N(w)表示噪声能量，P表示输出信号总能量．

基于社会模拟算法较快的收敛速度和较强的全局搜索能力，以信噪比为自适应随机共振的评价指标，搜索系统参数的全局最优值，实现微弱信号的检测．基于社会模拟算法的系统参数优化具体步骤如下：

（1）设定“follower”规模、迭代次数和变量个数．设“follower”的人群个数Pop，最大迭代次数K，多稳态势函数被优化参数的个数N；

（2）初始化“follower”．确定参数a, b, c的寻优范围，在该范围内随机生成第k=0代所有“follower”；

（3）计算初始化的所有“follower”的适应度值（随机共振系统输出信号的信噪比），并将最大值赋予leader；

（4）更新“follower”．经（4）式计算每个“follower”与“leader”之间的差距“difference”，再通过（5）式更新每一个“follower”和计算其适应度值，并判断其是否大于leader，若大于，则更新leader，反之，不更新；

（5）若满足终止条件（超过最大迭代次数K），则转至（6），否则转至（4）；

（6）输出最优“follower”（信噪比最大时的系统参数最优组合），并将参数带入随机共振系统，实现微弱信号检测．

综上所述，基于社会模拟算法的多稳态随机共振轴承故障诊断流程如图2所示．

图 2 基于社会模拟算法的多稳态随机共振轴承故障诊断流程图Fig 2 Fault diagnosis flow chart of multi-stable stochastic resonance based on social mimic optimization algorithm

3 工程应用

本次实验验证所用数据来自美国Case Western Reserve University 轴承数据中心，轴承型号为6205-2RS JEM SKF 深沟球轴承，其相关参数见表1．轴承实验信号的采样频率为12 kHz，选取的采样数据长度为24 000，驱动轴转速n=1 750 r/min，所选轴承内圈故障深度尺寸为0.177 8 mm，根据轴承内圈故障频率经验公式可得f0=157.5 Hz，图3为轴承内圈故障信号的时域图和频谱图，且信噪比SNR=−29.207 5．对故障信号进行Hilbert包络解调，其包络谱如图4所示．由图3的时域图中看不出信号的周期性，由于轴承故障特征信号被调制的缘故，在频域图中也找不到故障频率．只从包络谱中也不能准确的进行故障诊断，由于极低频率信号的幅值较为突出（远超过了特征频率），且在f0=157.5 Hz周围还有很多频谱线，很难准确判断．

表1 6205-2RS JEM SKF 深沟球轴承相关参数（单位：mm）Tab 1 Relevant parameters of deep groove ball bearing 6205-2RS JEM SKF

图3 原始轴承故障信号Fig 3 Original bearing fault signal

根据所提方法，设过滤低频区信号对故障信号干扰的高通滤波器带宽B= 30，在频率交换[8]的过程中所用到的高通滤波器、低通滤波器和带通滤波器的带宽也是B= 30，基准低频为10 Hz，变换载波频率为147.5 Hz．设变尺度过程中频率压缩比为200，二次采样频率变为fsr=12 000/200 Hz=60 Hz，随机共振的计算步长h= 1/fsr，故障特征频率for= 10/200 Hz=0.05 Hz．设人群（follower）的数量为30，最大迭代次数为50，设非线性系统参数[17]为a= [0,30]，b=[0,10]，c=[−10,10]．由社会模拟算法优化系统参数，经9次迭代后就得到系统最佳参数组合为a=3.509 1，b=0.113 3，c=−1.462 4，将最优参数带入多稳态随机共振系统，获得如图5所示的时域图和频域图，且信噪比SNR=−2.462 4．从时域中能清晰的看到故障信号的周期性，在频谱图的区域放大，图中能够清晰的看到故障特征频率是唯一且最突出的谱线，实现了轴承的故障诊断，验证了所提方法的有效性．通过压缩还原和频率交换，将低频区的故障特征频率恢复到高频区，如图6所示，能清晰的看到突出的故障特征频率．图6中的频率幅值与图5（b）有偏差，这是因故障特征频率恢复到高频区时，低通滤波和频率变换的影响．

图4 原始轴承故障信号的包络谱图Fig 4 Envelope spectrum of original bearing fault signal

图5 基于社会模拟算法优化的系统输出信号Fig 5 System output signal optimized based on social mimic optimization

为了证明社会模拟算法的优越性，采用粒子群算法对多稳态随机共振系统的参数进行优化．设粒子群规模数量也为30，最大迭代次数也为50，学习因子c1=c2= 2，初始惯性权重w=rand，惯性权重上下限为w1=0.9，w2=0.4[12]，其他参数一样．由粒子群算法优化系统参数，经25次迭代后就得到系统参数最佳组合为a=14.812 4，b=9.346 8，c=0.380 0（由于变尺度压缩的存在，在参数优化时数据点数变成原始点数的200倍，优化时间均稍微较长，所以并未在优化时间上作比较）．将最优参数带入多稳态随机共振系统，获得如图7所示的时域图和频谱图，且信噪比SNR=−4.825 4．从时域图中大概能看到故障信号的周期性，但是不清晰，在频谱图的区域放大，图中能够清晰的看到故障特征频率是唯一且突出的谱线，能实现轴承的故障诊断，但是从整个频域上来看，还存在大量高幅值的谱线，从而未能使时域图的故障特征信号的周期性清晰显现．通过频率交换，将低频区的故障特征频率恢复到高频区，如图8所示，能清晰的看到突出的故障特征频率．但其幅值小于图6中的频率幅值（也可以用图5（b）与图7（b）的中频率幅值相比较），说明其噪声的转化率不高，也说明粒子群算法优化所得的系统参数不如社会模拟算法，亦证明社会模拟算法的优化性能优于粒子群算法．

图6 故障特征频率恢复到高频区后的频谱图Fig 6 Frequency spectrum of fault characteristic frequency recovered to high frequency

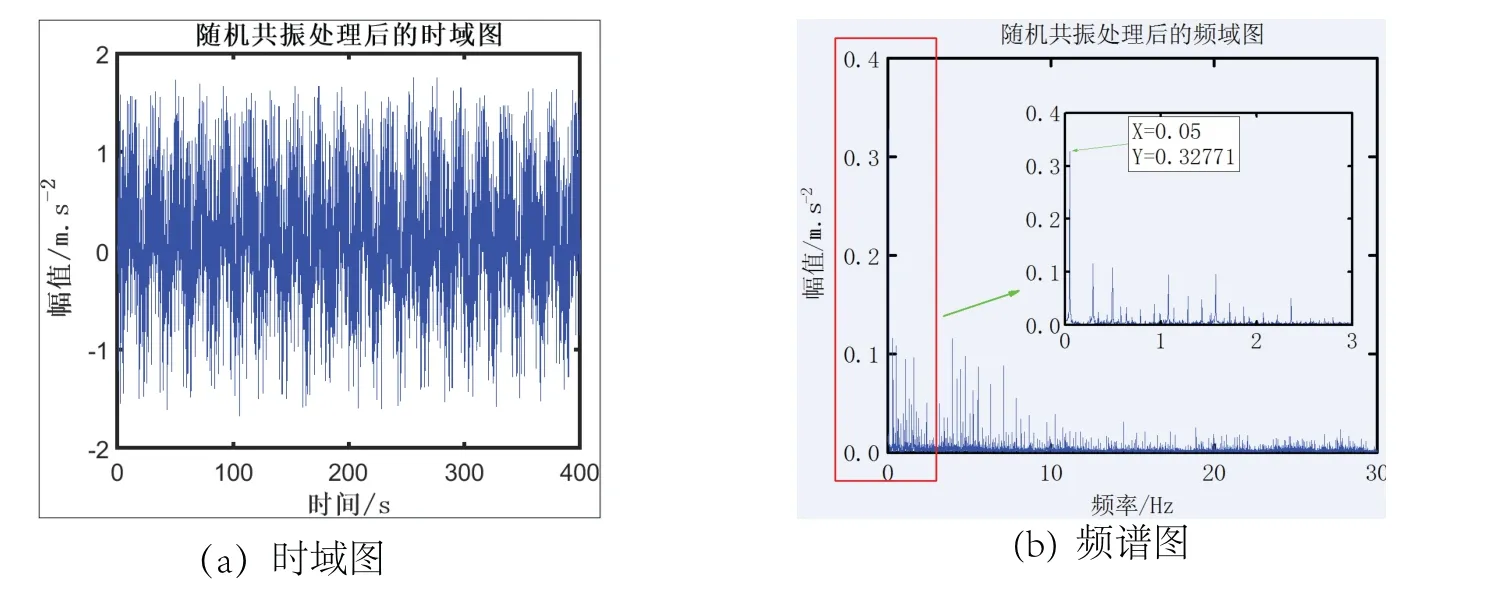
图7 粒子群算法优化的系统输出信号Fig 7 System output signal optimized by particle swarm optimization

图8 故障特征频率恢复到高频区后的频谱图Fig 8 Frequency spectrum of fault characteristic frequency recovered to high frequency

4 结论

经过对比优化系统参数达到最优所需迭代次数、系统输出故障特征幅值以及信噪比，得出社会模拟算法优于粒子群算法，具有优化收敛速度更快，全局搜索能力更强的特点，能够搜索到最佳的系统参数组合．

对具有调制特点的轴承故障信号进行Hilbert包络解调，并将经过频率交换和变尺度变换的包络信号作为多稳态随机共振系统的输入，能实现轴承微弱故障诊断，因此所提方法具有一定的工程应用价值．