Total Domination Versus Total Outer Connected Domination in Trees∗

ZHUANG Wei

(School of Applied Mathematics,Xiamen University of Technology,Xiamen Fujian 361024,China)

Abstract: Total domination number γt(G), is one of the most important domination parameters, which was introduced by Cockayne et al. in 1980. In recent years,a variant of total domination number have been extensively studied,namely,total outer connected domination number γtc(G). It is well known that γt(G)≤γtc(G). In this paper,we show that if T has no strong support vertex,we have thatIn addition,we provide a constructive characterizations of the trees achieving equality in the bound.

Key words: total domination;total outer connected domination;tree

0 Introduction

LetG=(V,E) be a simple graph without isolated vertices, and letvbe a vertex inG. The open neighborhood ofvisN(v)={u∈V|uv∈E}and the closed neighborhood ofvisN[v]=N(v)∪{v}. The degree of a vertexvisd(v)=|N(v)|. For two verticesuandvin a connected graphG,the distanced(u,v)betweenuandvis the length of a shortest(u,v)-path inG.The maximum distance among all pairs of vertices ofGis the diameter of a graphGwhich is denoted bydiam(G). A leaf ofGis a vertex of degree 1, and a support vertex ofGis a vertex adjacent to a leaf. A support vertex that is adjacent to at least two leaves we call a strong support vertex. A subdivided star is a graph obtained from a star on at least two vertices by subdividing each edge exactly once.

Total domination is one of the most important domination parameters. A total dominating set of a graphGwith no isolated vertex is a setSof vertices ofGsuch that every vertex inV(G) is adjacent to at least one vertex inS. The total domination number ofG,denoted byγt(G),is the minimum cardinality of a total dominating set ofG. A total dominating set ofGof cardinalityγt(G)is called aγt(G)-set. A survey of total domination in graphs can be found in [1]. In recent years,some parameters which are closely related to total domination have been extensively studied. In this paper,we mainly study one of them,namely,total outer connected domination,which is a variant of total domination.

The study of total outer connected domination in graphs was initiated in[2].A setDis a total outer connected dominating set ofGifDis a total dominating set ofGand the subgraph induced byV(G)Dis connected. The minimum cardinality of a total outer connected dominating set inGis thetotal outer connected domination number,denoted byγtc(G). A total outer connected dominating set ofGof cardinalityγtc(G)is called aγtc(G)-set. It is well know thatγt(G)≤γtc(G).

In this paper,we show that ifThas no strong support vertex,we have thatIn addition,we provide a constructive characterization of the trees achieving equality in the bound.

1 Total domination versus total outer connected domination in trees

Our aim in this section is to investigate the ratio between total domination number and total outer connected domination number,and present a constructive characterization of the families of trees achieving the upper bound.

From the definitions of total domination number and total outer connected domination number,we have the following observations.

Observation 1[3]LetGbe a connected graph that is not a star. Then,there is aγt-set that contains no leaf ofG.

Proposition 1[4]LetDbe aγtc-set of a connected graphGof ordern≥3 and minimum degreeδ(G) = 1. ThenDcontains all support vertices ofG. If moreoverγtc(G)≤n−2,thenDalso contains all leaves ofG.

Theorem 1LetTbe a nontrivial tree,we have that 1

In this theorem,both of the lower bound and the upper bound are optimal.Clearly,and Cyman et al.characterize the extremal trees in[5].

On the other hand,given any treeT,and construct a sequence of treesT0(=T),T1,T2,···,the treeTi+1is obtained fromTiby adding a vertex and joining it to one of the support vertices ofTi,i=0,1,2,···. By Observation 1,the total domination number of the resulting trees have never changed in this process, but from Proposition 1 and the definition of total outer connected domination number,the total outer connected domination number is constantly increasing. It means that when the numbernis sufficiently large,the ratioi s close to ∞. So we will discuss the trees which have no strong support vertex in this section.

For our purposes, we define a labeling of a treeTas a partitionS= (SA,SB,SC) ofV(T) (This idea of labeling the vertices is introduced in[6]). We will refer to the pair(T,S)as a labeled tree. The label or status of a vertexv,denoted sta(v),is the letterx∈{A,B,C}such thatv∈S x.

I didn t understand the words, nor did most of us. For we were not the German Afrikakorps but the British Eighth Army---the Desert Rats. Yet we were captivated by this mysterious voice that somehow reached deep into our thoughts and memories.

Let U be the family of labeled trees that:

(i)contains(P4,S0)whereS0is the labeling that assigns to the two leaves of the pathP4statusC,and to the two support vertices statusA;

(ii)is closed under the operation P1that is listed below,which extend the treeT′to a treeTby attaching a tree to the vertexv∈V(T′).

Operation P1: Letvbe a vertex with sta(v) =A. Add a pathv1v2v3v4, a vertexuand the edgesuv2,uv. Let sta(v1)=sta(v4)=C,sta(v2)=sta(v3)=Aand sta(u)=B(Fig 1).

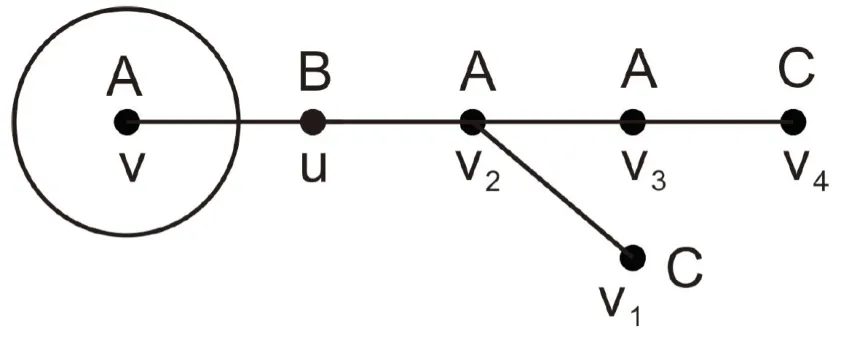
Fig 1 The operation P1

Let(T,S)∈T be a labeled tree for some labelingS.Then there is a sequence of labeled trees(P4,S0),(T1,S1),···,(Tk−1,Sk−1),(Tk,Sk)such that(Tk,Sk)=(T,S). The labeled tree(Ti,Si)can be obtained from(Ti−1,Si−1)by the operation P1.

In what follows,we present a few preliminary results.

Observation 2LetTbe a tree of order at least 4 andSbe a labeling ofTsuch that (T,S) ∈U. Then,Thas the following properties:

(b)A vertex is labeledCif and only if it is a leaf;

(c)SB∪SCis a independent set ofT,and

(d)The setSAis the uniqueγt-set ofT;

(e)Take anyx∈SB∪SC,and the setV(T){x}is aγtc-set ofT.

From Observation 2(c),2(d)and 2(e),the following corollary can be derived immediately.

Corollary 1LetTbe a nontrivial tree andSbe a labeling ofTsuch that(T,S)∈U. Then

Theorem 2LetTbe a nontrivial tree which has no strong support vertex,we have thatwith equality if and only if(T,S)∈U for some labelingS.

ProofWe proceed by induction on the ordernofT(As mentioned above, we only need to consider the trees which have no strong support vertex). The result is immediate forn≤4. Letn≥5 and assume that for every treeT′satisfyingwe have,with equality if and only if(T′,S′)∈U for some labelingS′.

The result holds when diam(T)≤3. Moreover,ifthen. Hence,we may assume that diam(T)≥4. LetP=v1v2···vtbe a longest path inTsuch thatd(v3)as large as possible. We know thatd(v2)=2. LetDbe aγt-set ofTcontaining no leaf,thenv2,v3∈D. If(N(v3){v2})∩D≠∅,then letT′=T−{v1,v2}andRbe aγtc-set ofT′. We have thatγtc(T′)+2 ≥γtc(T)andγt(T)−1 ≥γt(T′). It means thatSo we consider the case that(N(v3){v2})∩D=∅.

Claim 1d(v3)=2.

Assume thatd(v3)>2, thend(v3) = 3 andv3is a support vertex ofT. Suppose thatd(v4)>2, andu1is a neighbor ofv4outsideP. Then, the component ofT−u1v4containingu1, sayT1, is either a path of length 3,u1u2u3, or a path of length 4,uu1u2u3(Each of the other cases is either similar to the case we have argument or contradicting to the assumption that(N(v3){v2})∩D=∅). In either case, letT′be the component ofT−v4u1containingv4. Then,γtc(T′)+4 ≥γtc(T)andγt(T)−2 ≥γt(T′). It means that

Hence,d(v4) = 2. And then, letT′andT′′be the component ofT−v4v5containingv5andv4, respectively. Then,andγt(T)−2 ≥γt(T′).It means tha.Suppose next thatThen we have equality throughout the above inequality chain. In particular,andγtc(T′)+5=γtc(T). By induction,(T′,S′)∈U for some labelingS′. Ifv5has statusBorCinS′,then by Observation 2(e),R′=V(T′){v5} is aγtc-set ofT′, and moreover,R′∪(V(T′′){v4}) is a total outer connected dominating set ofT. That is,γtc(T′)+4 ≥γtc(T),a contradiction. Thus,v5has statusAinS′. LetSbe obtained fromS′by labelingv1and the leaf-neighbor ofv3with labelC,v2andv3with labelA, andv4with labelB. Then,(T,S)can be obtained from(T′,S′)by operation P1.Thus,(T,S)∈U.

By Claim 1, we have thatd(v3) = 2. Ifd(v4) ≥3, letube a neighbor ofv4outsideP. Due to (N(v3){v2})∩D= ∅and the choice ofP, the component ofT−uv4containinguis a pathP3, whereuis one of the leaves of this path. LetT′=T−{v1,v2,v3}whend(v4)≥3,andT′=T−{v1,v2,v3,v4}whend(v4)=2. Similar to the above argument,we always have that