Consensus of Multi-Agent Systems with Directed Intermittent Communications∗
YU Zhiyong,YU Shuzhen,JIANG Haijun
(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: This paper studies the consensus of second-order multi-agent systems (MASs) with general directed intermittent communications. Firstly,a directed spanning tree transformation method is applied to get the consensus error system. Moreover,some consensus conditions based on the coupling strengths and the communication width are obtained by using the Lyapunov stability theory and matrix inequalities. Finally,a numerical example is given to verify the theoretical result.
Key words: multi-agent systems;consensus;directed intermittent communications
0 Introduction
Last decades have witnessed the rapid development of cooperative control for MASs. This research field includes consensus control,rendezvous control,formation control and so on. The consensus of MASs,as one of the most important research topics,has received much attention since it has been widely applied to various areas,such as traffic control,sensor networks,mobile robots and unmanned aerial vehicles[1−4].
The consensus means that a number of agents achieve agreement about some variables of interests, such as position,velocity, and attitude by communicating with all agents. The main task of consensus is to devise the protocols which only rely on neighbor’s information. One pioneer work on consensus of MASs is[5],in which a general framework of first-order consensus was proposed. The existing consensus works can be simply categorised into leaderless consensus and leaderfollower consensus. In [6], the intermittent saturated controller was designed to study the semi-global leader-following consensus. The leader-following consensus with intermittent control and adaptive control was considered in[7].These works concerned leader-following consensus on directed graphs. However,many research works on leaderless consensus of MASs mainly focused on some special graphs, such as undirected graph[8], strongly connected graph[9], balanced graph[10], and so on. For general digraphs,the linear MASs with periodic intermittent communication was considered in[11]. However,there is still little work on consensus of second-order MASs with aperiodically intermittent communication and general nonlinear dynamics.
This paper aims at proposing a novel method to study consensus of second-order MASs with general directed communication. Compared with existing works,the main contributions of this paper can be summarized as follows: (1)According to the reordering scheme, a directed spanning tree transformation method is derived, which can transform the consensus problem into the stability of the zero solution of the error system. (2)For second-order MASs with general digraphs and nonlinear dynamics,a directed and aperiodically intermittent communication protocol is designed and some criteria for reaching consensus are obtained.
1 Preliminaries and Model formulation
For convenience,some notations are given in this section.Rnis then-dimensional Euclidean space. N+denotes the set of positive integer numbers.INis the identity matrix with dimensionN.1and0are column vectors with each entry being 1 and 0,respectively.ONdenotes theN-dimensional zero matrix. For a matrixC,Cijrepresents its entry in theith row andjth column. For a matrixB,BT,λmin(B)andλmax(B)represent its transpose,the minimum and the maximum eigenvalues ofB,respectively.B>0 meansBis a positive definite matrix. ‖·‖is the Euclidean norm. ⊗represents the Kronecker product.diag(·)denotes the diagonal matrix.
Consider a second-order MAS with inherent nonlinear dynamics,in which thei-th agent is described by
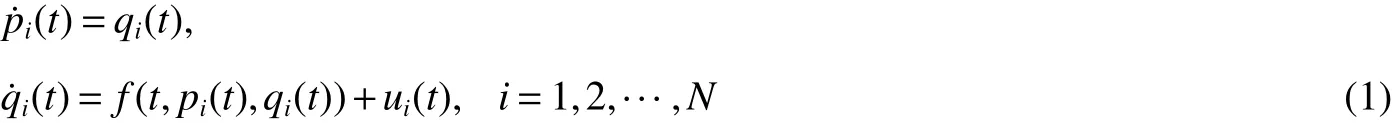
wherepi(t)∈Rn,qi(t)∈Rn,andui(t)∈Rnare the position state,velocity state,and the control input.f:R+×Rn×Rn→Rnis a continuously differentiable vector-valued function which represents the inherent nonlinear dynamics.
In the following,some related definitions and assumptions are given.
Definition 1[12]in which thei-th row of ˜Mhas only one entryαiand only one entry −αiwithαi≠0,and other entries are zeros. Let
Definition 2[13]The consensus for second-order MAS(1)is said to be reached if for any initial conditions,
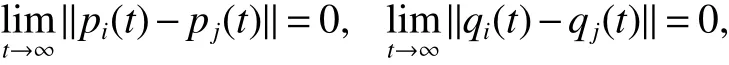
wherei,j=1,2,···,N.
Assumption 1For anyp,y,q,µ∈Rnandt≥0,there exist two nonnegative constantsρ1andρ2such that
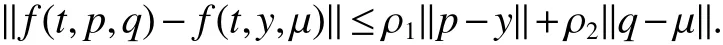
Assumption 2The communication graphG=(V,E,A)contains a directed spanning tree,andis a directed spanning tree ofG.
Remark 1The reordering scheme proposed in [12] is also applied. In the directed spanning tree, all nodes are divided into three categories:the root,the stem,and the leaf. In the directed spanning tree,we denotevikas the parent node of nodevk+1for 1 ≤k≤N−1,then(vik,vk+1)is a directed edge ofSpecially,whenk=1,vik=v1,andviik−1represents the parent node ofvik. Then the following lemmas are given.
Lemma 1[12]Suppose that the digraphG= (V,E,A) contains a directed spanning treeis the weighted adjacent matrix. The element ofsatisfiesand,otherwise. LetHbe an(N−1)×Nmatrix and its element satisfies
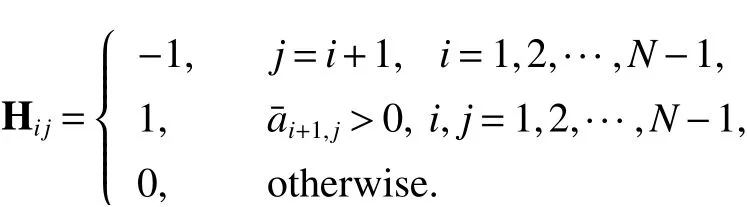
Then,the consensus for second-order MAS(1)can be realized if and only if
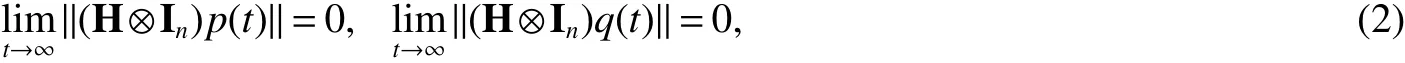
where
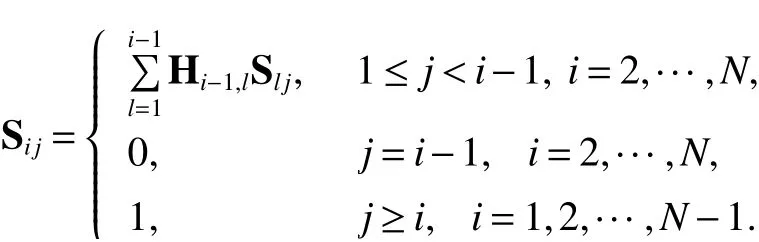
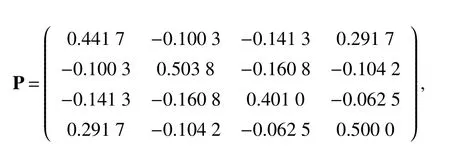
Lemma 3If Assumption 1 holds,then for any matrix Λ>0,there exists a symmetric matrixP>0 such that

ProofBecause ofGcontaining a directed spanning tree,all eigenvalues ofLhave positive real parts except for a simple zero eigenvalue[14]. Based on the analysis of Lemma 2, all eigenvalues ofKhave positive real parts, so the matrix −Kis Hurwitz. Hence,there exists a symmetric positive definite solutionPsatisfying the Lyapunov equation(3).
2 Main Results
The system(1)with aperiodically intermittent communication is described as follows
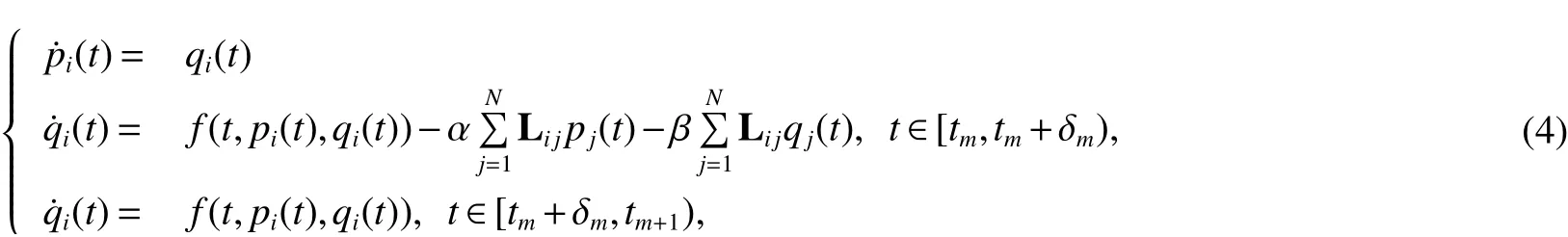
whereαandβare coupling strengths,δm,denotes the communication width in themth time interval,m∈N+andt1=0.


The error dynamics of system(4)is written as
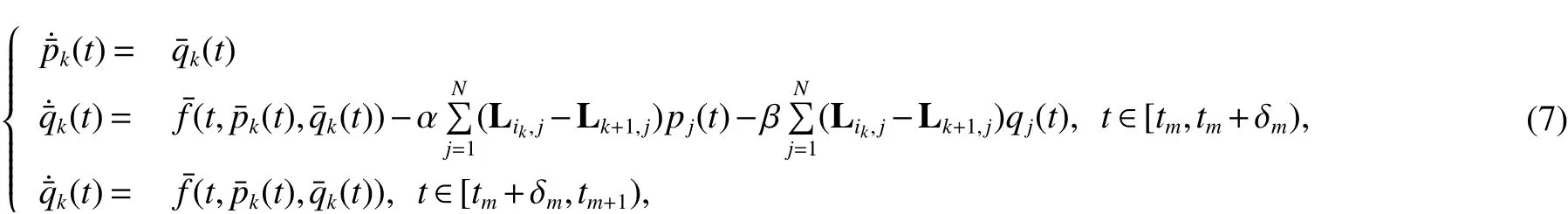
Oh, did not the youngest sister listen eagerly to all these descriptions? and afterwards, when she stood at the open window looking up through the dark blue water, she thought of the great city, with all its bustle25 and noise, and even fancied she could hear the sound of the church bells, down in the depths of the sea
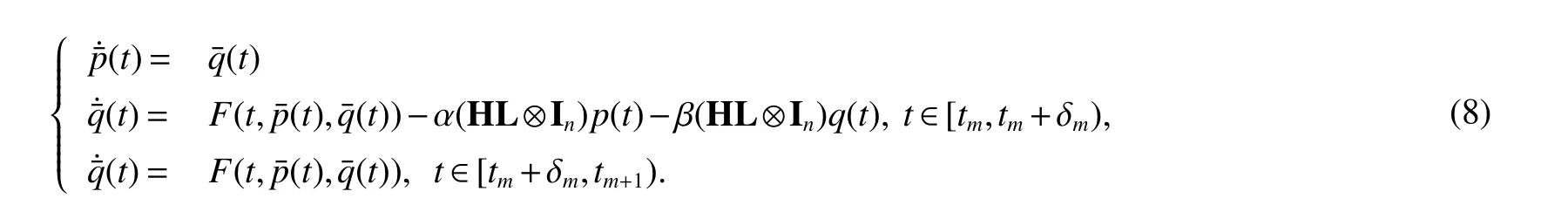
Theorem 1Under Assumption 1 and Assumption 2,the second-order MAS(4)can achieve consensus if the following conditions are satisfied

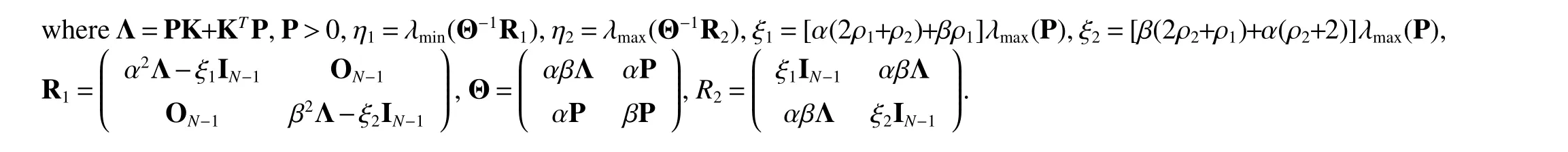
ProofWe consider the following Lyapunov function candidate
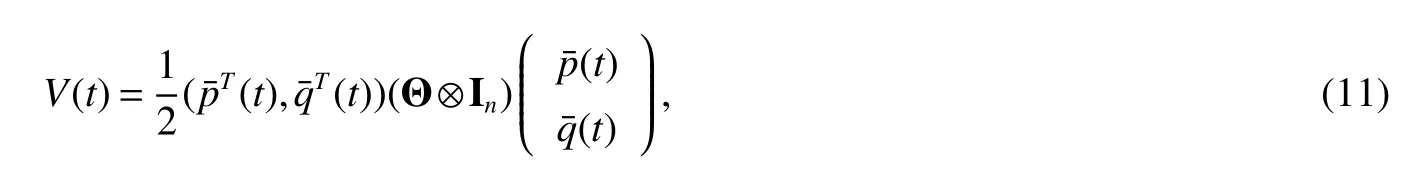
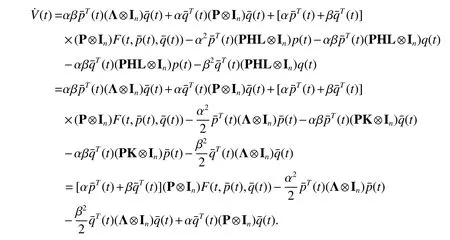
Based on Assumption 1,it has
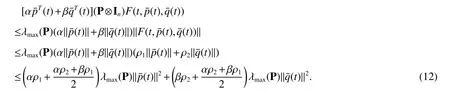
In combination with(13),the equation(12)is written as
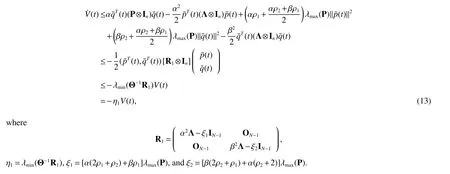
Fort∈[tm+δm,tm+1),m∈N+,based on Assumption 1,the time derivative ofV(t)with equation(8)is
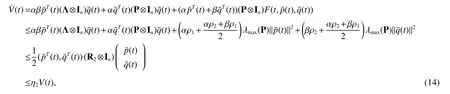
where
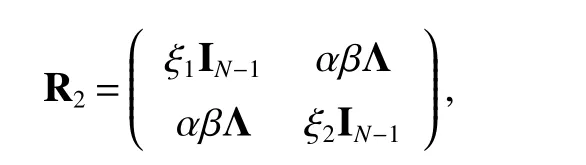
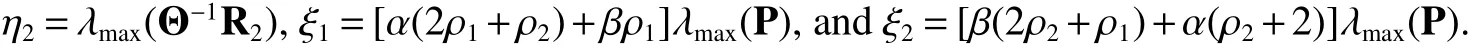
In combination with the above process,we have
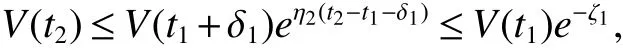
whereζ1=η1δ1−η2(t2−t1−δ1). Applying the mentioned condition(10),one getsζ1>0. Employing induction,it has that,for any positive integerm,
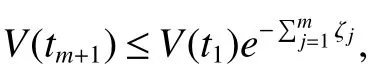
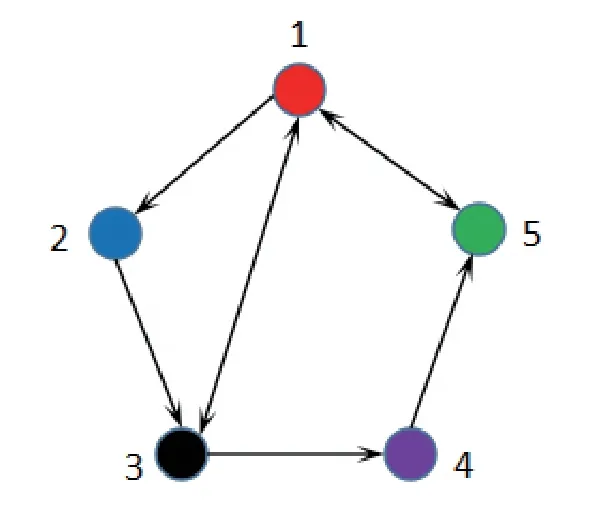
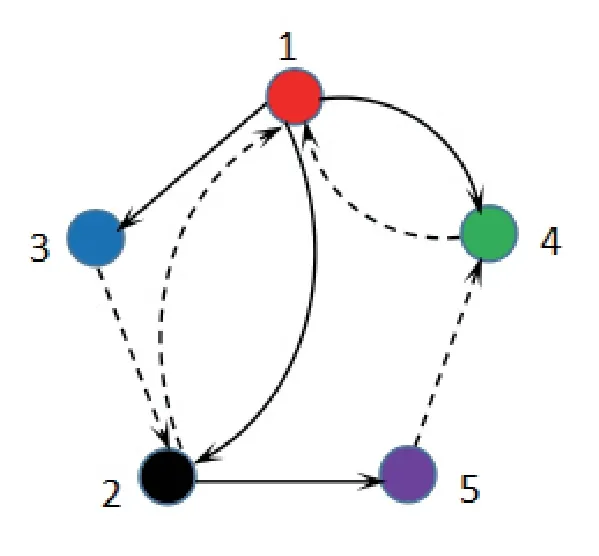
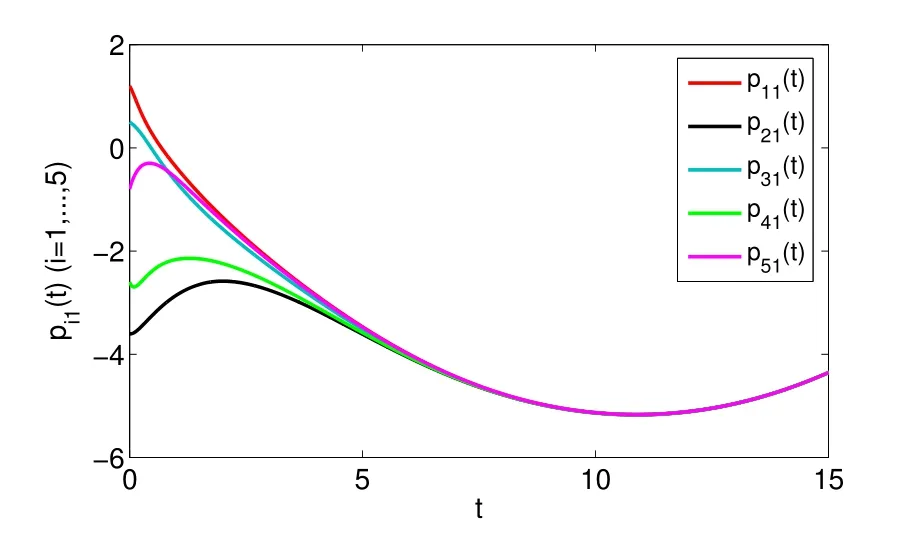
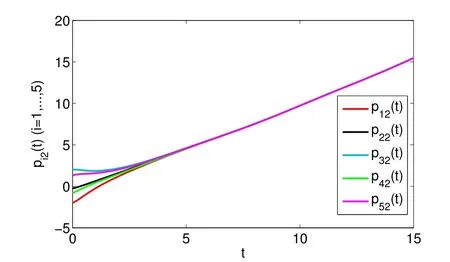
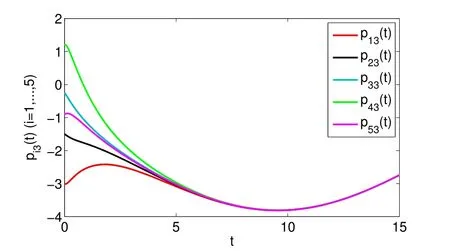
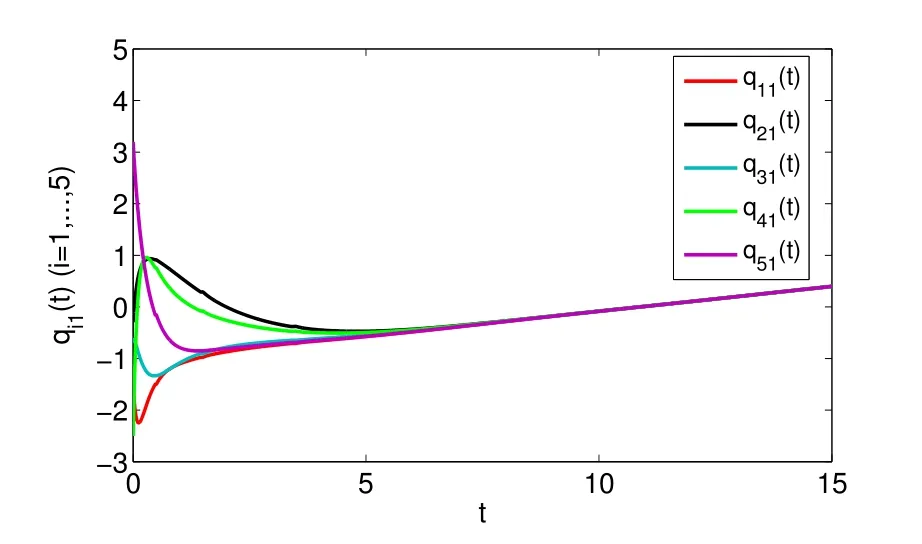
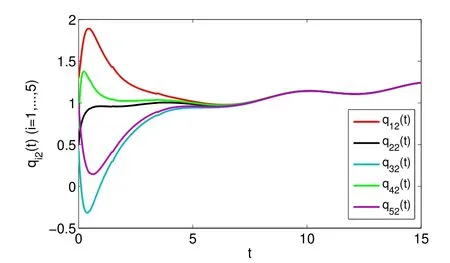
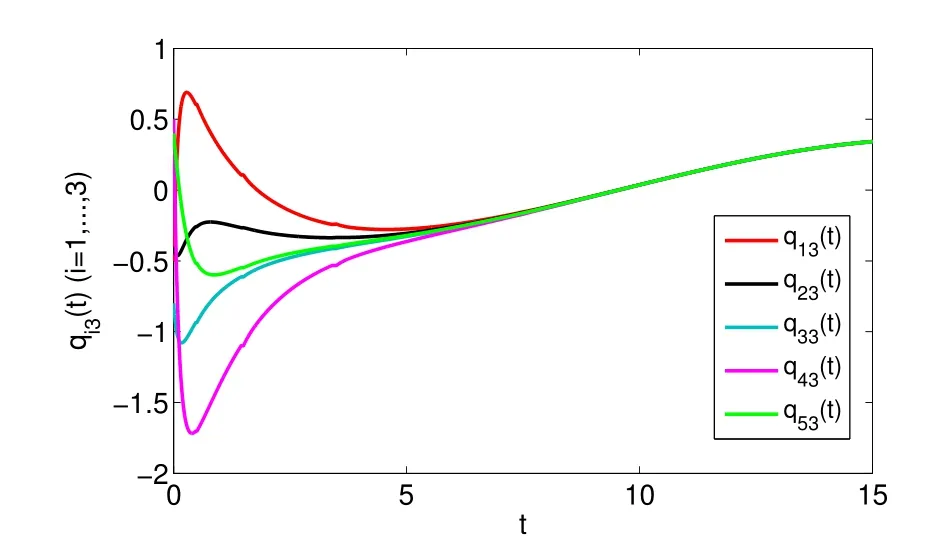
whereζj=η1δj−η2(tj+1−tj−δj)>0,j=1,2,···,m. For arbitraryt>0,there existss∈N such thatts+1≤t whereK0=eωmaxη2V(t0),which indicates that all agents exponentially reach consensus. In order to illustrate the effectiveness of the protocol,a simulation example is presented. Consider the MAS(4)with five agents. The information communication among all agents is described by Fig 1 with the weight on each edge being 1. By reordering scheme,the communication graph is given as Fig 2,where the solid lines denote the directed spanning tree. The nonlinear function isf(t,pi(t),qi(t))=0.05sin(pi(t))+0.05cos(qi(t)),wherepi(t),qi(t)∈R3,i=1,···,5. It is easy to verify that Assumption 1 is satisfied. According to Lemma 2,one has Choose α= 2, β= 3, then it is easy to get thatξ1= 0.378 3,ξ2= 3.825 2,λmin(Λ) = 0.999 6>max{0.094 6,0.425 0}. By simple calculation, one obtainsη1=0.563 7η2=9.540 0, and=0.944 2. Hence, we choose=0.95. Then the conditions of Theorem 1 are satisfied.Choosing the initial conditionsp1(0)=(1.2,−2,−3)T,q1(0)=(−1.5,1.3,−0.5)T,p2(0)=(−3.6,−0.25,−1.5)T,q2(0)=(−0.3,0.5,−0.4)T, p3(0)=(0.5,2,−0.25)T,q3(0)=(−0.6,0.45,−0.8)T, p4(0)=(−2.6,−0.8,1.2)T,q4(0)=(−2.5,0.7,0.5)T, p5(0)=(−0.8,1.3,−0.9)T,andq5(0)=(3.2,1,0.4)T.Then,all agents’state trajectories are presented in Figs 3~Figs 8. Fig 1 The graph G Fig 2 The reordered graph G Fig 3 Trajectories of pi1 Fig 4 Trajectories of pi2 Fig 5 Trajectories of pi3 Fig 6 Trajectories of qi1 Fig 7 Trajectories of qi2 Fig 8 Trajectories of qi3 In this paper,we employ a directed spanning tree transformation method to study the consensus of second-order MASs with nonlinear dynamics. A directed intermittent communication protocol is proposed, and some conditions to achieve consensus are obtained by using Lyapunov stability theory and inequality techniques.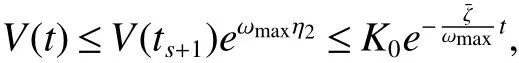
3 Numerical simulations

4 Conclusion

