不可压缩的Brinkman-Forchheimer方程的回溯两重网格法∗

王小娟, 贾宏恩

(太原理工大学 数学学院, 山西 晋中030600 )

0 引言

考虑不可压缩的Brinkman-Forchheimer方程:

其中：Ω是Rn(n=2或3)中有界连通并具有Lipschitz连续的区域, 其边界为∂Ω,u是流体速度,p是压力,ν>0是粘度系数,f是体力, Forchheimer项α|u|r−2u(2 ≤r<∞,α>0)是由Forchheimers定律导出的, 用来描述各种物理情况, 如多孔介质流动、摩擦效应以及某些耗散机制等.

方程(1)具有非线性和单调性. 近年来, 一些学者致力于Brinkman-Forchheimer方程数值分析的研究. 如文献[1]研究了Brinkman-Forchheimer方程的收敛性和连续依赖性; 文献[2]给出了求解这一问题的混合有限元方法,证明了弱解的存在唯一性并进行了误差估计; 文献[3]讨论了混合有限元方法的超收敛性, 也可参考文献[4-7].

文献[8]提出了求解非线性问题的两重网格法, 该方法先在粗网格上求解一个非线性方程作为细网格的迭代初值近似,然后在细网格求解线性问题,与传统的方法相比可以节省大量的计算时间,已被广泛应用于求解其他非线性方程[9−14]. 文献[15]提出求解Navier-Stokes方程的回溯两重网格法.

本文将采用回溯两重网格法求解问题(1). 该方法需要先在粗网上求解非线性方程,再在细网格上求解Stokes问题, 然后在粗网格上线性校正. 最后, 通过数值实验验证算法的有效性及稳定性.

1 符号和准备工作

Wk,p表示Sobolev空间,其中范数和半范为‖·‖k,p和|·|k,p.L2(Ω)上的内积空间定义为:

引进如下的双线性、拟线性和三线性形式:

并且有以下不等式成立[4−7]:

引理1[15]假设Ω的边界满足强Lipschitz条件, 下面三线性形式的不等式成立:

其中：当n=2时,s=∊>0(任意小); 当n=3时,

方程(1)的弱形式: 求(u,p)∈(X,M) 使得

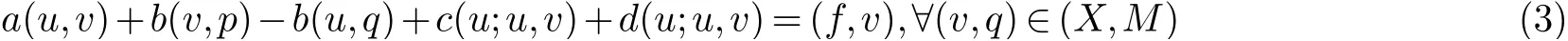
问题(3)的解的存在性和唯一性, 详见文献[7].

2 两重网格法

(A1) 对于∀(v,q)∈(Hk+1(Ω))2×Hk(Ω),k≥1, 存在(Iηv,Jηq)∈Xη×Mη使得

‖v−Iηv‖0≤Cηk+1‖v‖k+1, ‖v−Iηv‖1≤Cηk‖v‖k+1, ‖q−Jηq‖0≤Cηk‖q‖k, 其中C是与η无关的正常数.

(A2) LBB条件: 存在与η无关的正常数β使得, 其中η=H或h.

方程(3)的混合有限元格式是: 求(uη,pη)∈Xη×Mη使得

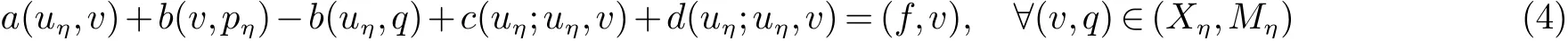
问题(4)的存在性、唯一性及收敛性分析, 参见文献[7].

引理2[6−7,15]设(u,p),(uη,pη)(η=h或H)分别是方程(3)和(4)的解,对于有:

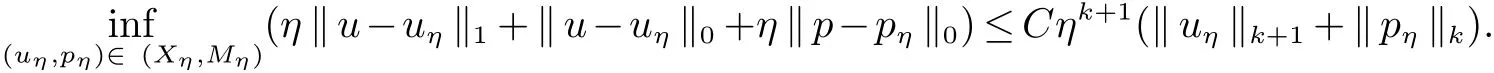
下面给出两重网格法:

步骤1: 求(uH,pH)∈(XH,MH), 使得对于∀(v,q)∈(XH,MH)有

步骤2: 求(uh,ph)∈(Xh,Mh), 使得对于∀(v,q)∈(Xh,Mh)有

步骤3: 求(eH,εH)∈(XH,MH), 使得对于∀(v,q)∈(XH,MH)有

其中：u∗=uh+eH, p∗=ph+εH.

为了便于分析, 将内积空间定义为:Yη=(Xη,Mη)(η=H或h)和Y=(X,M), 定义范数为, 并引入连续双线性形式AH:Y×Y→R和BH:Y×Y→R使得

则两重网格法的步骤2和步骤3可以改写为:AH和BH在Y×Y上连续且依赖于|uH|1. 当H足够小, 可以证明|uH|1≤|uH−u|1+|u|1≤CH(|u|2+|p|1)+|u|1≤C(u,p). 并且AH和BH满足[15]:

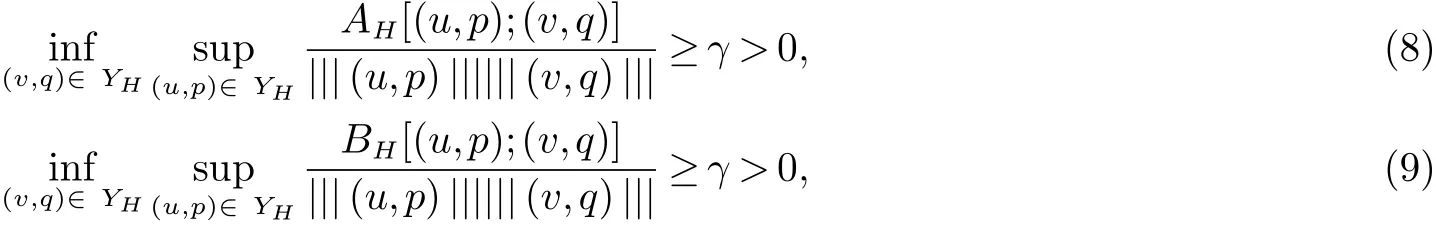
引入Galerkin投影(Q,R): Y→YH满足BH[(w,t);(v−Q(v,q),q−R(v,q))]=0,∀(w,t)∈YH,(v,q)∈Y.

为了导出v−Q(v,q)的L2估计, 令(φ,ϕ)∈Y满足

因为u是非奇异解, 所以(φ,ϕ)存在唯一. 若(10)是H2正则的, 则对∀f∈(L2(Ω))n, 解

引理3若u是非奇异解, 则(Q,R)满足:

证明(I) 利用(9)式和BH的连续性得：

然后利用三角不等式证明.

(II) 令(φf,ϕf)为(10)式的解, 对于右边f=v−Q(v,q)∈(L2(Ω))n. 通过计算

设w=v−Q(v,q),t=q−R(v,q), 然后利用投影性质, (2)式, 引理1, 引理2和嵌入定理得：

再利用上述不等式和插值不等式得:

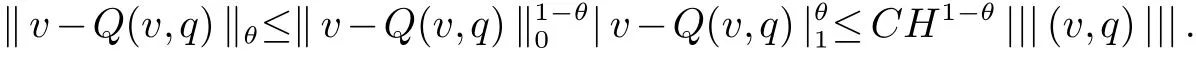
(III) 当(v,q)∈Y∩((H2(Ω))n×H1(Ω))时, 利用(IHv,JHv)∈YH和(8)式得：

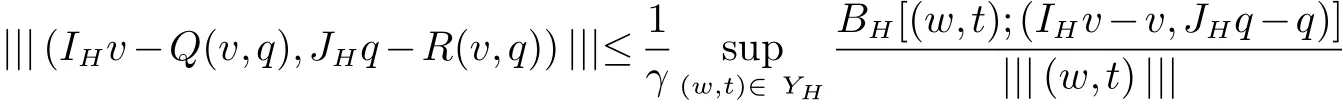
然后, 利用三角不等式和插值的性质得：

再重复以上步骤并利用(11)式得:

最后, 利用插值不等式和(12)式证明结论.

3 能量误差估计

定理1假设XH⊂Xh⊂X,MH⊂Mh⊂M满足逼近性假设及LBB条件. 记(u,p)为(3)式的解且则有:

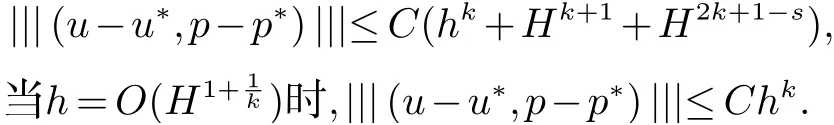
其中:u∗=uh+eH,p∗=ph+εH,C为常数. 当n=2时,s=∊>0(任意小); 当n=3时,

证明首先, 考虑步骤2之后的误差, 误差满足:

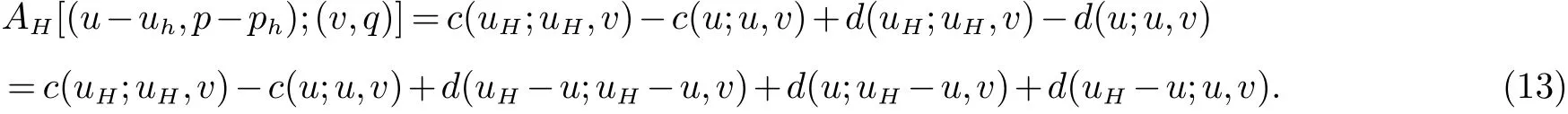
由(13)式及AH的连续性得:

根据三角不等式, (A1), (2)式, (8)式, (14)式, 嵌入定理, 引理1和引理2得:

利用(3)式和(6)式得:

然后, 由(3)式, (7)式和(Q,R)的定义得:

(17)式减去(16)式, 且u∗=uh+eH,p∗=ph+εH得:

再由三角不等式, (A1)和(9)式得：

记

然后, 利用(2)式, 嵌入定理, 引理1, 引理2和引理3分别估计Sj(j=1,···,11):

最后, 将(19)式代入(18)式证明定理.

4 数值算例

在这部分进行数值实验. 第一个例子是用光滑精确解验证算法的收敛阶. 第二个例子是用方腔驱动流证明算法的稳定性. 另外, 我们将比较标准有限元算法和两重网格法的CPU时间. 所有的算法都是用有限元软件FreeFem++[16]实现.

4.1 收敛测验

问题(1)的精确的解:

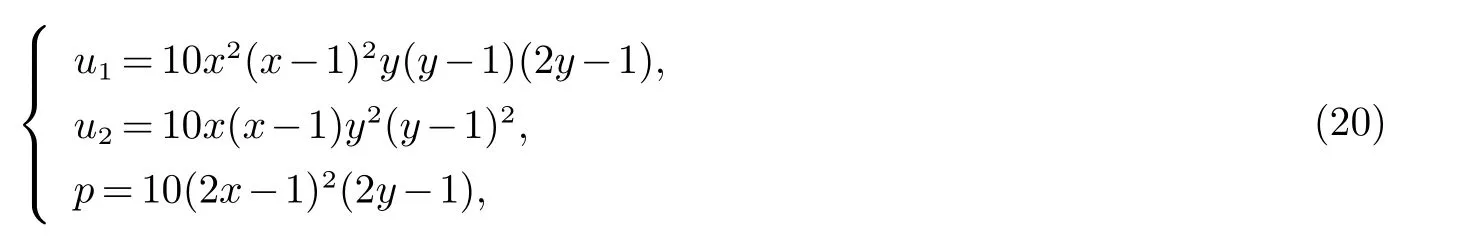
其中f是将精确解代入(1)式所得.

取Ω=[0,1]×[0,1],h=1/49,1/64,1/81,1/100,1/121, 采用P2−P1元时,取r=3,α=1,ν=0.1; 采用P1b−P1元时,取r=4,α=10,ν=1. 数值结果分别见表1～表6.

表1 利用P2 −P1元的标准有限元算法的数值结果Tab 1 The numerical results of the standard finite element method using P2 −P1 element

表2 利用P2 −P1元的两重网格法的数值结果Tab 2 The numerical results of the two-grid method using P2 −P1 element

表3 利用P2 −P1元的两种方法的CPU时间(单位: s)Tab 3 The comparison of the CPU times (unit: s) for two methods using P2 −P1 element

表4 利用P1b−P1元的标准有限元算法的数值结果Tab 4 The numerical results of the standard finite element method using P1b−P1 element

表5 利用P1b−P1元的两重网格法的数值结果Tab 5 The numerical results of the two-grid method using P1b−P1 element

表6 利用P1b−P1元的两种方法的CPU时间(单位: s)Tab 6 The comparison of the CPU times (unit: s) for two methods using P1b−P1 element

由表1、表2得: 采用P2−P1元时所有的收敛阶完全符合理论分析;由表4、表5知: 采用P1b−P1元时速度的收敛阶可以达到理论值, 而压力的收敛阶比理论分析高. 此外, 两种方法的收敛阶几乎相同, 但两重网格法比标准有限元方法节省了60%以上的CPU时间, 见表3和表6, 所以回溯两重网格法更有效.

4.2 方腔驱动流

在区域Ω=[0,1]×[0,1]上进行计算, 在没有其他体力的情况下, 流动是由施加在顶部边界上的切向速度场驱动的. 在∂Ω上施加速度的法向分量为零, 切向分量除沿顶部的边界设为1其余为零. 采用P2−P1元取h=1/25及不同的r,α,ν比较两种方法的CPU时间, 见表7. 然后取r=3,α=10,ν=1和r=4,α=10,ν=0.1分别描述两种方法的流线和压力等高线, 如图1～图4所示.

表7 两种方法的CPU(时间: s)比较Tab 7 The comparison of the CPU times (unit: s) for two methods

通过图1～图4和表7可以观察到: 这两种方法的流线和压力等值线几乎相同, 但两重网格法比标准有限元方法节省时间. 因此, 回溯两重网格法是稳定的并且比标准有限元方法更有效.

图1 标准有限元法的流线（左）和压力等值线（右）Fig 1 The streams (left) and pressure contours (right) of the standard finite element method

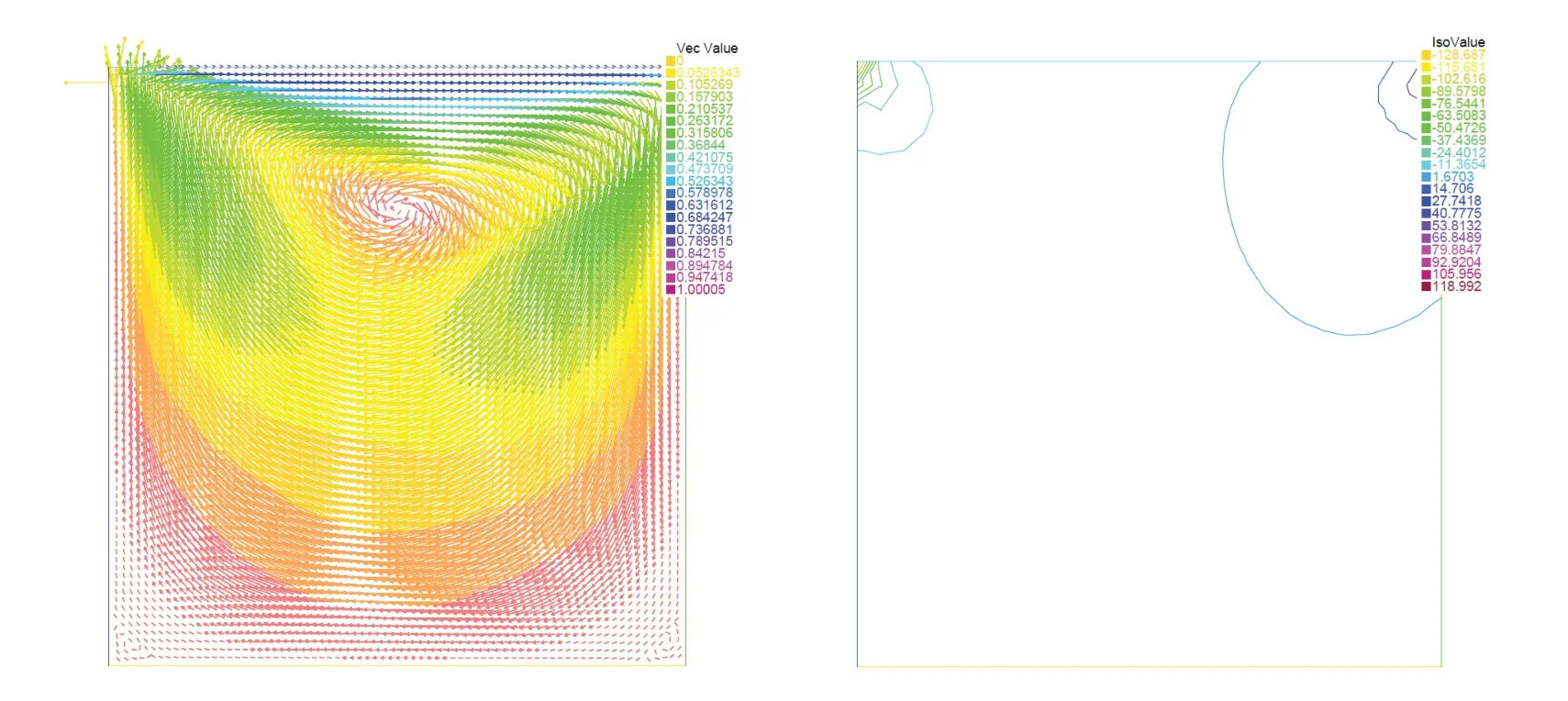
图2 两重网格法的流线（左）和压力等值线（右）Fig 2 The streams (left) and pressure contours (right) of the two-grid method

图3 标准有限元法的流线（左）和压力等值线（右）Fig 3 The streams (left) and pressure contours (right) of the standard finite element method

图4 两重网格法的流线（左）和压力等值线（右）Fig 4 The streams (left) and pressure contours (right) of the two-grid method

5 结论

本文讨论了不可压缩的Brinkman-Forchheimer方程的回溯两重网格法. 通过两个数值实验对理论分析进行验证，可知该算法是稳定的, 两种方法具有相同的收敛阶, 但是在保持相同的收敛阶时两重网格法可以节省大量的时间, 因此回溯两重网格法更有效.