基于L-R混沌系统和双重扩散的图像加密算法∗
费敏,李国东
(新疆财经大学统计与数据科学学院,新疆 乌鲁木齐830021)
0 引言
图像中包含的数据跟文本信息有很大区别,主要在于包含的数据量较为丰富且冗余度高.现如今,海量的文本、图片、音频以及视频在网络上传送,这些文件隐秘安全的传送引起学者们的重视.设计既安全又高效的加密算法是一项具有重大现实意义的研究课题,这关系到国家信息安全和人们隐私的安全.混沌因其具有很强的初值敏感性、有界和拓扑传递性、分岔和长期不可预测性、分数维特性以及内在随机性等特点,常用于图像加密.
马聪等[1]利用两个以上的混沌系统对明文做两次置乱扩散达到加密的目的,创新点在于对位级和像素级图像都进行了加密,加密步骤紧密相关,还加入了Hilbert置乱,该算法解决了加密时选用混沌系统结构单一的问题,能非常好地隐藏明文图像信息.王瑶等[2]为了解决当前加密方案使用单向扩散导致抗破译性能较弱的问题,将非线性S盒与双向扩散相结合设计一种密钥与明文相关的图像加密算法,不仅可以将图像内容高度隐藏,而且高效安全.牛莹等[3]运用改进的约瑟夫对图像置乱,运用DNA动态编码对图像扩散,还加入了密文反馈机制完成图像无损加密,算法创新点在于密钥、加密算法与明文紧密关联,能够抗数据丢失攻击,在密文信息被拦截攻击破坏时具有恢复能力,有效提高了算法的安全性,但是算法使用的混沌系统结构较为单一.
本文针对混沌系统结构相对单一,密钥、部分加密算法与明文无关,使用单向扩散导致加密算法安全性不高等问题,给出一种“双向扩散置乱”加密结构、密钥与明文关联的图像加密方案.其大致框架:首先,对超Lorenz混沌系统迭代生成混沌序列并对其预处理,从明文中选择部分像素点,并与选出的部分明文像素点运算共同产生第二级密钥;其次,利用三维Rossler混沌和第二级密钥生成加密需要的密码;最后,使用密码和三维Rossler映射对图像进行正-逆向扩散和置乱.仿真实验表明该算法在保证具有更高安全性的同时提升了加密效率.
1 混沌理论和约瑟夫问题
1.1 超Lorenz混沌[4]
超Lorenz混沌的动力学方程为

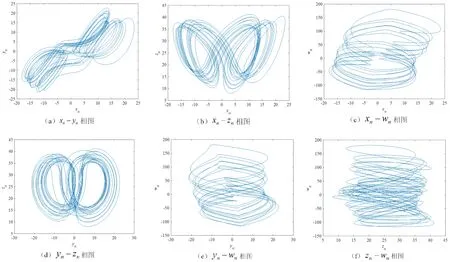
图1 超混沌Lorenz系统相图Fig 1 Phase diagram of hyperchaotic system
1.2 Rossler混沌
Rossler混沌系统最早在1976年被挖掘[8−13],将Rossler映射用在图像加密中.Rossler混沌方程组为

式(2)中:x,y,z为系统变量,a,b,c为系统参数;当a=0.2,b=0.2,c=5.7时,系统是混沌的,系统的复杂程度与参数a的取值呈正比.对超Lorenz混沌系统迭代生成序列,做预处理后作为方程组(2)的初始值,图2展示了迭代系统200 000次产生的混沌吸引子.
1.3 约瑟夫环问题的基本描述
这是一个循环遍历问题,编号为1,2,···,n的人按照顺时针方向围着一张圆桌坐在其周围,给定一个长度m,从编号为1的报数,到m的那个出局;从它的下一个继续从1报数,到m的那个继续出局;按照这个过程开始循环,循环到最后一个出局[12].将这一过程用函数表达,即f(n,m).其中:n为元素总数,m为步长.具体的例子,函数f(9,3)的解法是将1,2,3,4,5,6,7,8,9这些元素围成圈,按顺时针方向循环遍历并且删除第3个元素,被删除的元素顺序为3,6,9,4,8,5,2,7,1.郭毅等[12]将约瑟夫函数拓展为f(n,m,r,D,g), 其中:参数r为起点,D为循环方向,g为间隔[13].
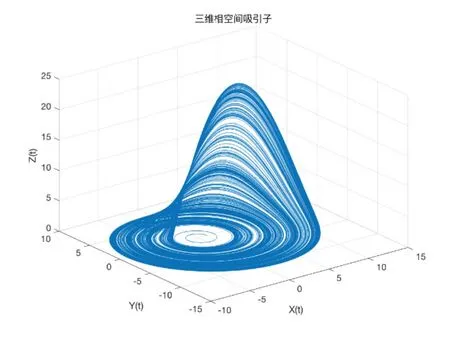
图2 L-R混沌系统奇异吸引子Fig 2 Singular attractor of L-R chaotic system
2 L-R双混沌系统的图像加密算法
2.1 加密流程
加密方案主要分成3个步骤:(1)正向扩散;(2)动态约瑟夫置乱;(3)逆向扩散.图3给出了加密流程.
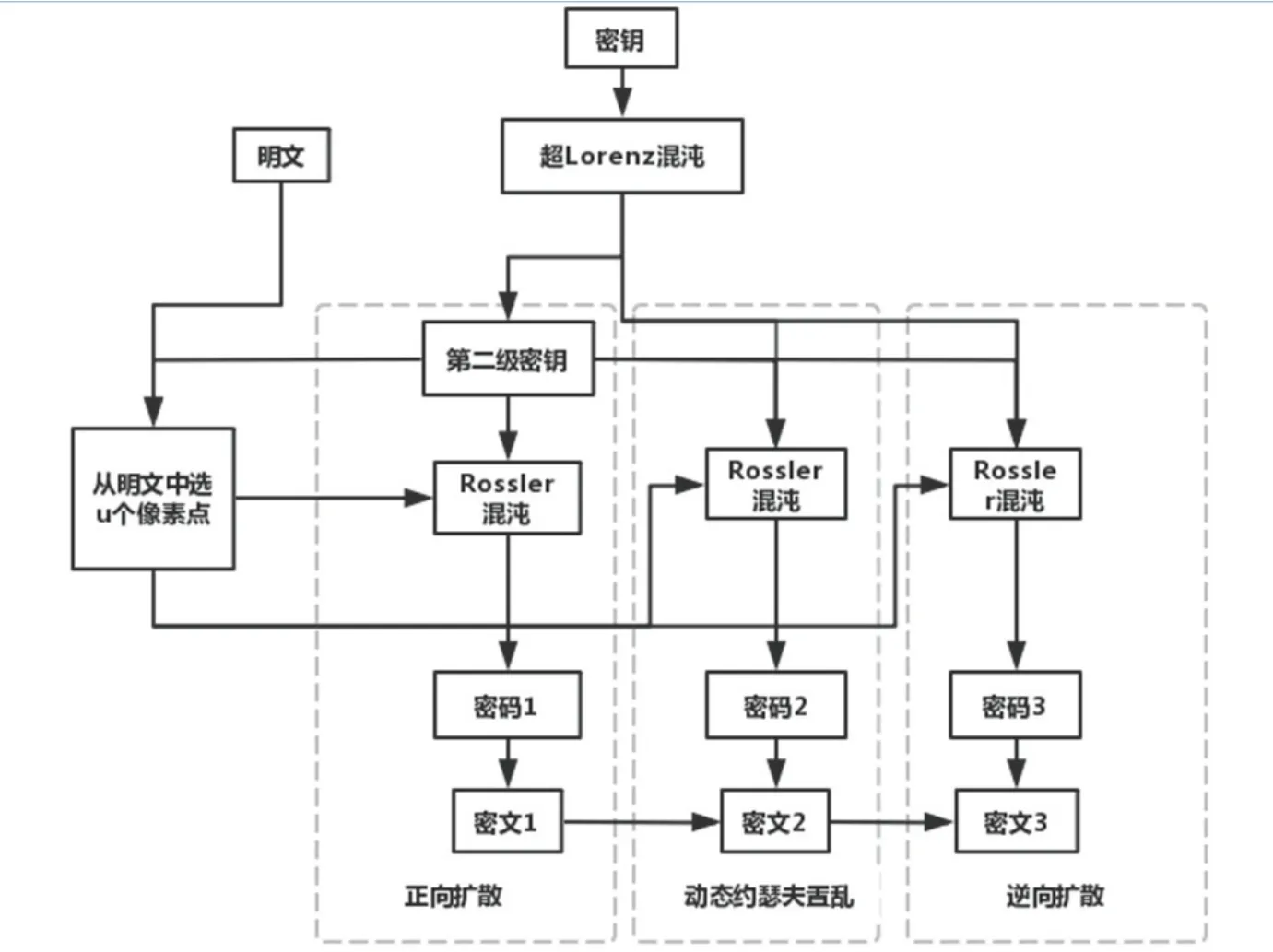
图3 图像加密流程Fig 3 Image encryption process
2.2 加密具体步骤
首先,通过初始密钥K来迭代超Lorenz混沌,运用产生的混沌序列通过给定的筛选规则从明文选出一部分像素点,用数学归纳法对前人的运算规则进行改进,运用改进后的运算规则和部分像素值运算,可得4条序列,将这4条序列做简单运算作为第二级密钥{x0,y0,z0};代入三维Rossler映射迭代得到3个混沌序列,其次按设定好的运算规则将其转化为整数序列,用来达到“双扩散-置乱”加密的目的,详细步骤如下:
步骤1首先读图,将大小记为m=M×N,其次,按从左到右再从上至下的扫描顺序扫描明文图像展开为一维向量,记做I={Ii|i=1,2,···,m}.
步骤2将初始密钥K={xL0,yL0,zL0,wL0}和系统参数值{a=10,b=8/3,c=28,r=−1}作为超混沌Lorenz映射的初始值和参数.使用四阶龙格库-塔法进行迭代式(1)r1+r2+2 000次跳过映射的过渡态;再迭代u次,得到4个序列,记为ua,ub,uc,ud,{uai,ubi,uci,udi|i=1,2,···,u},其次通过式(3)将序列ua,ub,uc,ud整数化,得到4个一维向量,记做ux,uy,uz,uw,即ux,uy,uz,uw,{uxi,uyi,uzi,uwi|i=1,2,···,u}.最后,继续迭代M×N次,得到4个序列,记做sx,sy,sz,sw,{sxi,syi,szi,swi|i=1,2,···,M×N}.
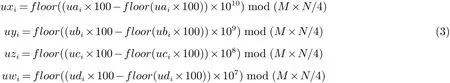
步骤3运用序列ux,uy,uz,uw和式(4)的运算规则从向量I中选择部分像素点放在PU中,即PU是一个1×u的向量.
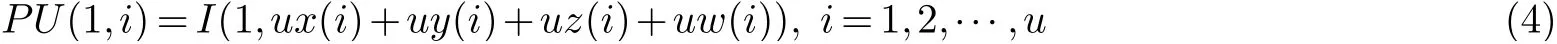
如果一维向量PU与混沌序列sx,sy,sz,sw用文献[6]“逐次相加取模运算”的计算规则,会增加加密所需要的时间;以序列sx和矩阵PU为例,其过程如图4所示.
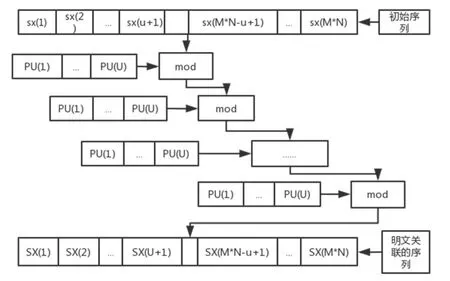
图4 所筛选像素与原始序列运算规则Fig 4 Operation rules of filtered pixels and original sequence
现对文献[6]中规则进行改进,先详细分析运算规则可得结论:因PU的大小已固定且小于序列sx的大小,则i∈[1,u−1],序列中第i个元素与PU的前i个元素集合对应;在i∈[u,M×N−u+1],序列中第i个元素与PU的u个元素集合对应;在i∈[M×N−u+2,M×N],序列中第i个元素与PU的后M×N−i+1个元素集合对应,图5为详细过程.具体改进方法如下:先算原始混沌序列中每一元素对应的明文像素点的值的总和,得到一条长为M×N的序列,具体过程由图6给出;其次对该序列和原始混沌序列做加法和取模运算得到新混沌序列.改进后能提升加密效率.
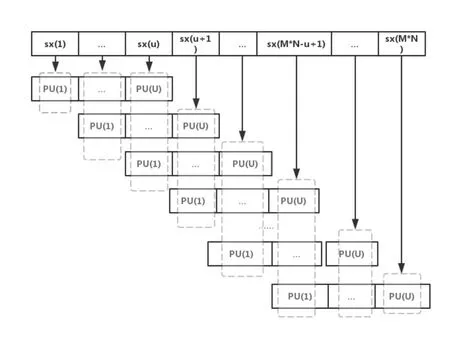
图5 筛选像素与混沌序列的对应规则Fig 5 Corresponding rules of filtering pixels and chaotic sequences
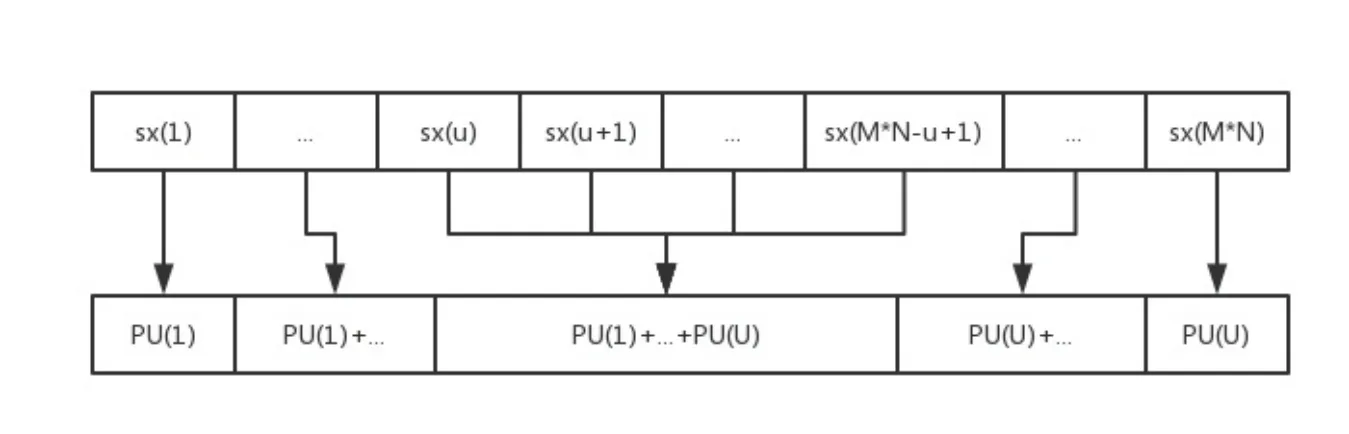
图6 混沌序列与筛选像素和的对应规则Fig 6 Corresponding rules of chaotic sequence and filtered pixel sum
步骤4借助式(5)分别计算序列sx每一个元素对应明文像素点集合的和值,得到M×N的一维向量,记为px,px={pxi|i=1,2,···,M×N}.
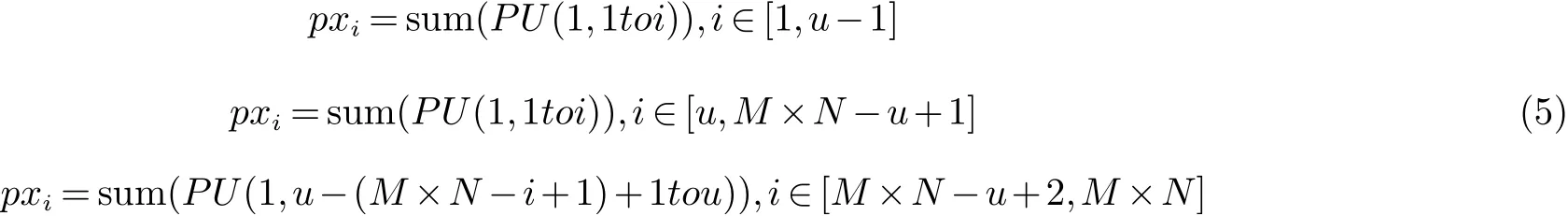
步骤5重复步骤4三次,计算出序列sy,sz,sw对应的一维向量py,pz,pw.
步骤6借助式(6)将序列sx,sy,sz,sw和px,py,pz,pw进行加法和取模运算,得到跟明文有关的序列,记做psx,psy,psz,psw,{psxi,psyi,pszi,pswi,|i=1,2,···,M×N},将其进行简单相加运算得到三条序列{psxi,+psyipsyi+pszi,pszi+pswi|i=1,···,M×N}作为三维Rossler混沌的初始值.

步骤7将三维Rossler映射初始值和系统参数a=0.2,b=0.2,c=5.7代入式(2),迭代步长为0.002,迭代次数为M×N,得到3个一维向量,记做xi,yi,zi,{xi,yi,zi|i=1,2,···,M×N}.其次通过式(7)将三条序列整数化,生成三条序列,记为X,Y,Z,{Xi,Yi,Zi|i=1,2,···,M×N}.
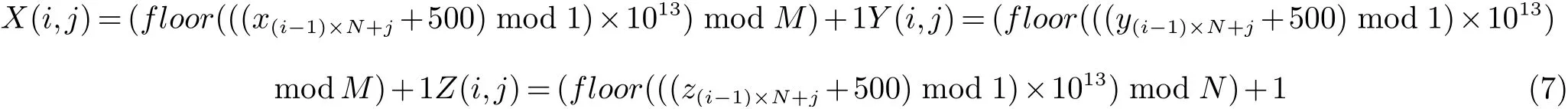
其中:i=1,2,···,M,j=1,2,···,N.
步骤8将序列X作为加密向量,运用式(8)和式(9)对I向量进行正向扩散,加密后的向量记为C1={C1,j,j=1,
···,M×N}.
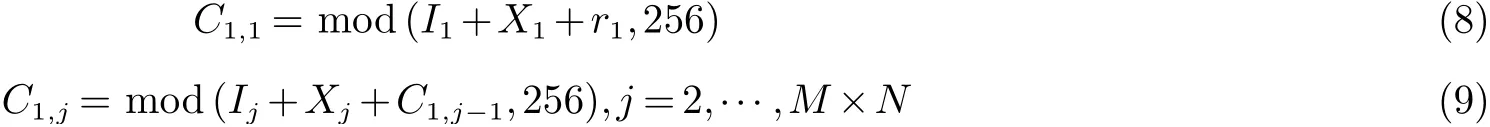
步骤9将C1转换为矩阵形式,用动态约瑟夫对C1图像置乱,将约瑟夫遍历与混沌系统结合,把约瑟夫遍历中的步长m拓展成为一个序列M(m1,m2,···,ms),在对约瑟夫圈进行遍历时,删除第i个元素时使用步长mi.为使步长不断变化,让混沌序列Y替代M序列,输入到约瑟夫函数中,对C1图像每行像素的位置按照约瑟夫遍历的顺序调整,再对C1图像中每列像素的位置按照约瑟夫遍历的顺序调整,得到的密文图像记为C2.
步骤10将序列Z作为加密向量,运用式(10)和式(11)对C2向量进行逆向扩散,加密后的向量记为C3={C3,j,j=1,···,M×N},将其转化为矩阵形式,记为最终密文图像D.
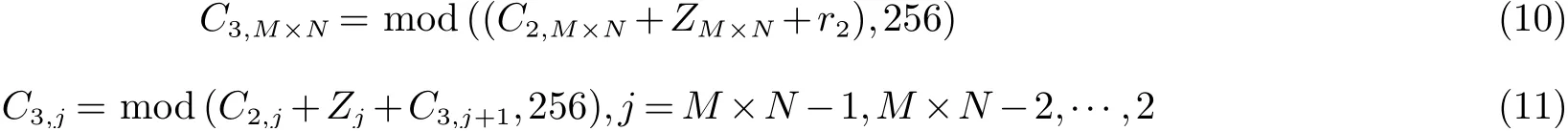
3 仿真
选用Lena图像进行实验仿真,所使用的计算机配置为4G内存,Windows7操作系统,1.90 GHz处理器,Lena图像的分辨率为256×256,大小为192 KB[14−17].算法在Matlab R2018a 环境下进行仿真,其中,超Lorenz混沌的参数设置为{a=10,b=8/3,c=28,r=−1},超Lorenz混沌初始密钥为K={xL0,yL0,zL0,wL0,r1,r2,u},数值为{xL0=3.313 3,yL0=12.054 6,zL0=40.887 9,wL0=−34.567 7,r1=89,r2=118,u=16},Rossler混沌参数是{a=0.2, b=0.2,c=5.7} ,图7给出仿真结果.

图7 实验结果Fig 7 Experimental results
4 加密算法安全性分析
4.1 速度测试
以灰度图像Lena例,大小为256×256,按照本文给出的算法加解密200次,计算平均加解密时间分别为0.755 8, 0.763 4,由表1可知,与文献[8]相比,本文设计的算法拥有更快的加密速度.

表1 本文与文献[8]的加解密时间Tab 1 Encryption and decryption time of this paper and reference [8]
4.2 直方图分析
图8给出直方图分析结果,从图8可以看出加密得到的密文像素值频率分布是非常均匀的,在一定程度上说明加密算法有将图像的统计特性隐藏的足够好的能力,说明算法具有抗统计攻击能力[18−20].
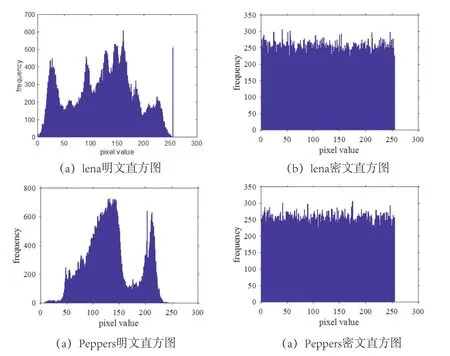
图8 明密文直方图Fig 8 Histogram of ciphertext
4.3 密钥空间及敏感性分析
衡量加密算法的好坏要计算它的密钥空间[21].密钥空间足够大才能抗穷举攻击.加密效率高的加密算法的密钥长度至少为2128,才有抵抗暴力破解的能力.加密方案初始的7个密钥分别是:{xL0,yL0,zL0,wL0,r1,r2,u},其中,xL0∈(−40,40),yL0∈(−40,40),zL0∈(1,81),wL0∈(−250,250),r1∈[0,255],r2∈[0,255],u∈[1,256];其中,xL0,yL0,zL0,wL0是浮点数,精度达到了10−15,而r1,r2,u则是整数,步长为1.即算法密钥空间具体是:2×40×2×40×81×2×250×(1015)4×256×256×256 ≈4×1075远远大于2128,因为210≈103,所以密钥空间4×1075≈2252,从表2可知,与文献[1]相比,给出的算法密钥空间更大,有抗穷举攻击的能力.

表2 本文与文献[1]的密钥空间Tab 2 2 Key space of this paper and reference [1]

图9 密钥敏感性测试Fig 9 Key sensitivity test
对超Lorenz混沌系统的初值进行2×10−14的微小扰动,当xL0=3.313 3+2×10−14时,图9(a)为解密得到的图像,说明给出的加密方案有很强的密钥敏感性,给密钥做肉眼看不到的微小改变都无法获得正确解密图.
4.4 明文敏感性分析
像素变化比率(简称NPCR)表示明文一个像素值变化密文像素值变化的比率,NPCR越接近100%,加密效果越好[22].D1表示密文,D2表示明文,公式为:

归一化平均改变强度(简称UACI)指两图全部对应位置像素点差值和最大差值比值的均值.UACI越接近33.4635%越好,公式为:
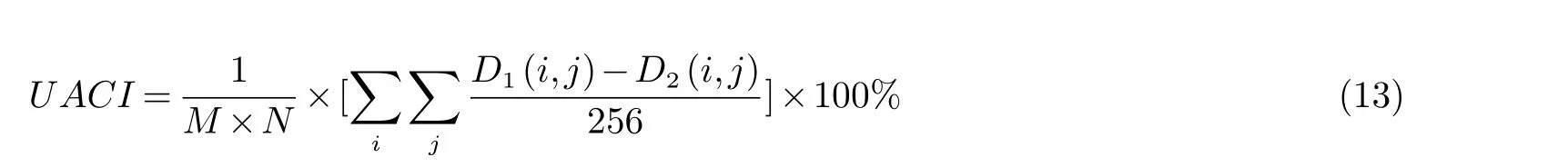
对明文中任意一点像素值进行非常微小的变动,通过计算,此时NPCR和UACI分别为99.83%和33.43%,均非常接近理想值,对比文献[1],结果如表3所示.

表3 明文敏感性分析Tab 3 Plaintext sensitivity analysis
4.5 相邻像素相关性分析
根据式(14),截取2 000对像素点(x,y)进行分析,计算结果如表4和图10.由表4、图10可知,明文图像相邻像素点相关性高,相关系数在1附近,密文图各方向像素间相关系数都在0附近,说明本文加密算法达到了理想效果.同文献[1]比较,本文给出的算法加密得到的密文相关性系数值更小,有抗基于相关特性攻击的能力.

式中:
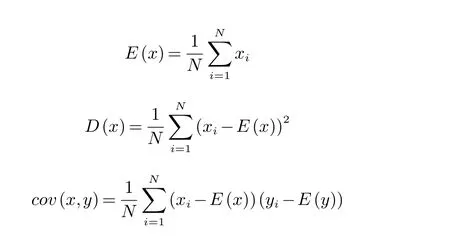

表4 明文和密文相邻像素间相关系数Tab 4 Correlation coefficients between adjacent pixels of plaintext and ciphertext
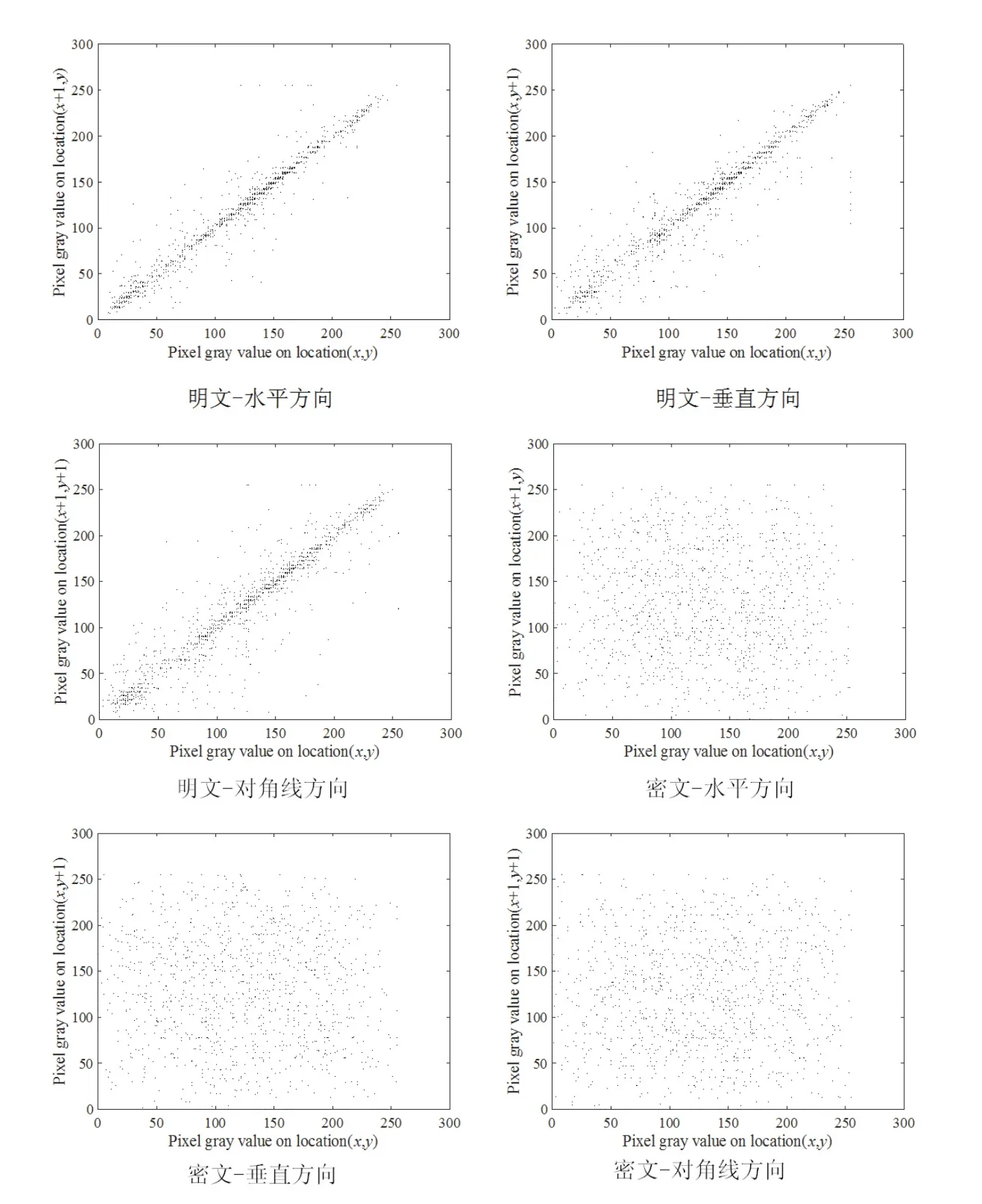
图10 明密文各方向相邻像素相关性Fig 10 10 Correlation of adjacent pixels in each direction of ciphertext
4.6 信息熵
根据Shannon定理,信息熵反映了一个序列的随机性[23].对256个灰度级的灰度图像而言,信息熵越靠近8越好.为体现加密方案较为优秀,对Lena图像的明文与密文信息熵进行对比,根据式(15)计算信息熵的结果见表5,式中m(i)指的是灰度值i出现的概率.由表5可知,与使用文献[1]中给出的加密算法生成的密文的信息熵相比,使用本文所给出的加密算法生成的密文信息熵更加接近理想值8,表明本文算法加密效果更好.


表5 信息熵结果Tab 5 Information entropy results
5 结论
本文给出的基于L-R混沌和双重扩散的图像加密算法的密钥与明文图像相关联,也就是给定相同的密钥但是不同的明文图像都会对应不同的密码.设定两级密钥和更加高效的运算规则来产生混沌序列.此外,该算法运用约瑟夫遍历与混沌系统相结合,使约瑟夫遍历中步长不断发生变化的方法来置乱图像.加密体系结构为“正向扩散-动态约瑟夫置乱-逆向扩散”.通过Matlab实验分析说明算法具有高的加密效率与高的安全性,密文直方图呈现均匀分布,具有很强的抗统计、差分和穷举攻击能力,安全性高,并且该算法解决了混沌加密系统结构单一以及与明文无关的问题.

