函数空间的拓扑结构

2021-05-29 01:37杨寒彪杨忠强

汕头大学学报（自然科学版） 2021年2期

杨寒彪，杨忠强

（1.五邑大学数学与计算科学学院，广东江门 529020；2.汕头大学理学院数学系，广东汕头 515063）

1 引言

函数空间是众多数学分支的研究对象，例如，泛函分析，复分析，拓扑学等.一般来说，函数空间由一族函数的集合上赋予各种结构后得到.例如，赋予代数结构后可以得到向量空间，赋予度量和拓扑后可以得到度量空间和拓扑空间.也可以把线性结构和拓扑结构结合后得到拓扑线性空间等.

本文希望总结一些我们了解的关于函数空间的拓扑结构问题的答案.这个问题的一般形式为：设X，Y是两个赋予一定结构的集合，例如，拓扑结构，线性结构等.F（X，Y）表示从X到Y的一些映射所构成的集合，例如，连续映射等.我们希望探讨在F（X，Y）上赋予一个自然的拓扑Γ后得到拓扑空间FΓ（X，Y）的拓扑结构，即，证明这个空间同胚于哪个经典的空间.当然，为了完成这个工作，对空间FΓ（X，Y）的性质的探讨也是必不可少的.在几乎所有的情况下，空间FΓ（X，Y）都是无限维的（当Y是零维拓扑空间时，往往是例外），所以无限维拓扑学的方法对解决这个问题是举足轻重的，这个问题也构成了无限维拓扑学发展的重要动力之一.

本文中，R是实数集合并赋予通常拓扑和序，I＝[0，1]，N＝{1，2，…}是R的子集，并遗传R的拓扑和序，Rn是n-维Euclidean空间.

我们定义几个常见的无限维空间，这些空间是我们需要的典型空间和模型空间.Hilbert方体是指乘积空间Q＝[－1，1]N.进一步，我们能定义它的以下子空间：

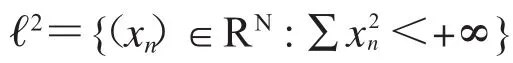
2 同胚于ℓ2的空间

设X是紧度量空间，Cu（X，R）表示从X到R的全体连续函数且赋予一致收敛拓扑，那么，众所周知，Cu（X，R）是一个可分的Banach空间.

我们首先看Fréchet提出的一个问题：

问题 2.1.（Fréchet问题）ℓ2≈RN是否成立

Anderson在文献[1]中证明了ℓ2≈RN.从而肯定的回答Fréchet问题.Anderson论文的关键之处是给出了Hilbert方体Q的吸收子等概念，为无限维拓扑的创立开启了大门.所以，我们有必要介绍一下这个概念.

首先，我们介绍Z-集的概念，Z-集是无限维拓扑学的基本概念之一，由Anderson在文献[2]中给出.其来源于几何拓扑学，是有限维拓扑学中边界集在无限拓扑学的对应概念.设X是拓扑空间，A是X中的闭集，若对X的任意开覆盖U，存在连续映射f:X→XA使得（f，idX）≺U，则称A是X中的Z-集，这里idX表示X上的恒等映射，（f，idX）≺U表示对任意的x∈X，存在U∈U使得f（x），idX（x）∈U.这时，我们称f和idX是U接近的.用Z（X）表示X中所有Z-集构成的集族.可以表示为可数多个Z-集之并的集称为Zσ-集.文献[1]证明了Q中的Z-集有下面的重要性质：

定理2.1.（Q中Z集的无扭性质）设A，B∈Z（Q）且A≈B，则存在同胚h:Q→Q使得 h（A）＝B，即（Q，A）≈（Q，B）.

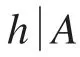
定理2.2.设 L，M是Q的两个吸收子，则（Q，L）≈（Q，M）.

Anderson还证明了 B（Q）和Σ都是Q的吸收子.因此（Q，B（Q））≈（Q，Σ）.利用上面的结论，Anderson在文献[1]给出了下面的结果：

定理 2.3.（Anderson定理）ℓ2≈RN.

几乎同时，Kadec在文献[4]证明了，所有与ℓ2不同胚的可分无限维Banach空间都同胚于RN，于是结合二者我们可以得到：

定理2.4.（Anderson-Kadec定理）所有可分无限维Banach空间都同胚于RN.

推论2.1.若X是无限紧度量空间，则Cu（X，R）≈RN.

进一步，定理2.4被推广为：

推论2.2.所有可分的，无限维的，拓扑完备的局部凸拓扑线性空间都同胚于RN.

上述推论中，局部凸的条件能否去掉曾经是无限维拓扑学研究的最重要的未解决问题之一.1994年，Cauty在文献[5]中给出了一个例子说明了这个条件不可去掉.

3 Hilbert方体流形的拓扑特征及其应用

我们知道Hilbert方体Q与Hilbert空间ℓ2是两个最重要的无限维空间.更一般的，我们可以定义Q-流形与ℓ2-流形.设X是可分度量空间，若X存在一个开覆盖U使得U中成员都是同胚子Q（相应的ℓ2）中一个开集，则称X是Q-流形（相应的ℓ2-流形）.上世纪70年代在60年代工作的基础上对Q-流形和ℓ2-流形进行了深入的研究得到了很多深刻的结果.由于这些工作使得无限维拓扑学登堂入室了，也对确定函数空间的拓扑结构问题起到非常大的作用.不相交的胞腔性质（下面简写为DCP）是Toruńczyk在文献[6]中引入的.设（X，d）是度量空间，若对任意的自然数n，对任意的连续映射f:In×{0，1}→X，X 的任意开覆盖 U，存在连续映射 g:In×{0，1}→X 使得（f，g）≺U且g（In×{0}）∩g（In×{1}）＝，则称X有DCP.1971年，Anderson和Chapman在文献[7]中把定理2.1推广到Q-流形上，得到了Q-流形中Z集的无扭定理.

定理3.1.（Q-流形中Z集的无扭性质）设M是紧的Q-流形，A是紧空间.F:A×I→M是一个同伦且F0和F1是Z-嵌入（即他们都是嵌入且其像是M中Z-集），则存在同伦H:M×I→M使得：

（i）.H0＝idM；

（iii）.对任意的t∈I，Ht:M→M是同胚.

对于空间Q＝M中任意两个同胚的Z-集C，D，我们一定能找到一个满足定理3.1条件的A＝C和同伦F:A×I→Q使得F（0A）＝C且F（1A）＝D，从而定理3.1确实推广了定理2.1.定理3.1说明了M中两个“同伦”的Z-集（即定理3.1的假定中的F的存在性）F（0A）和F（1A）可以通过一个M上同胚实现.但是不同于Q，定理2.1对Q-流形M是不成立的.即若C，D是M中两个同胚的Z-集，则未必有（M，C）≈（M，D）.例如，M＝Q⊕Q×S1，这里S1是单位圆周.任取点p∈Q和q∈Q×S1，则{p}≈{q}且他们都是M中的Z-集，但显然（M，{p}）（M，{q}）.1969年，Anderson和 Schori在文献[8]中证明了Q-流形的稳定定理：

定理3.2.（Q-流形的稳定定理）设M是紧的Q-流形，则M×Q≈M.

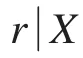
定理3.3.令M是紧的Q-流形，X是一个ANR，f:M→X是胞腔像的，则f可以用同胚逼近的充分必要条件是X有DCP.

利用映射梯的工具，Edward证明了每一个紧的ANR与Q的乘积都是Q-流形在胞腔像映射下的像（Miller-West定理），每一个紧的ANR都与一个多面体同伦等价.最后，Toruńczyk在文献[9]（参考文献[10]）中证明了划时代的结果：

定理3.4.（Toruńczyk Q-流形特征定理）设X是紧度量空间，则X是Q-流形当且仅当X是有DCP的ANR.

定理3.5.（推论）设X是度量空间，则X≈Q当且仅当X是有DCP的AR.

对于U⊂X，令

由{U-，U＋:U 在 X 中开}在 Cld（X）生成的拓扑称为 Viectoris拓扑，记为 CldV（X）.由{U-，（XC）＋:U在X中开且C在X中紧}在Cld（X）生成的拓扑称为Fell拓扑，记为CldF（X）.几乎与Toruńczyk给出他的特征定理的同时，Curtis和Schori在文献[11]利用West的一个定理证明了超空间定理：

定理3.6.（Curtis-Schori-West超空间定理）.设X是度量空间，CldV（X）≈Q当且仅当X是非平凡的Peano连续统，即，连通的，局部连通的紧度量空间.

在文献[12]中，我们把这个定理推广的非紧的度量空间，证明了下面的定理：

进一步，如果X是可数多个有限维的闭子空间的并，那么有

在文献[13]中，Banakh和Voytsitskyy回答了我们的一个问题，证明了：

定理3.8.设X是度量空间，那么

当且仅当X是局部紧的，非紧的，局部连通的，不含紧连通分支的度量空间且可以表示为可数多个有限维的闭子空间的并.

苏轼（宋）有诗云：“横看成岭侧成峰，远近高低各不同.不识庐山真面目，只缘身在此山中”.当我们视X中的一个闭集为它的特征函数后，我们可以认为定理3.6，定理3.7和定理3.8给出了从X到{0，1}的上半连续函数的子集在一种自然的拓扑下的拓扑结构.这个观点对于理解后面两节的内容是有用的.

4 HIilbert空间ℓ2-流形的拓扑特征及其应用

进一步，Toruńczyk在文献[14]（参考文献[10]）中给出了类似于定理3.5的ℓ2-流形的特征定理.首先，我们需要一个定义.设X是可分度量空间，我们说X有强离散性质是指对X的任意开覆盖U，对于任意的连续映射f:Q×N→X，存在连续映射g:Q×N→X 使得（f，g）≺U且{g（Q×{n}）:n∈N}是 X 中的离散子集族.

定理4.1.（Toruńczyk ℓ2-流形特征定理）可分度量空间X是ℓ2流形当且仅当X是拓扑完备的有强离散逼近性质的ANR.

利用上面特征定理，我们可以确定很多函数空间的拓扑结构.例如，在文献[15]，酒井证明了：

定理4.2.令X是非平凡的紧度量空间，Y是可分完备的ANR且不含孤立点，那么，赋予紧开拓扑的函数空间Cco（X，Y）是一个ℓ2-流形.

设X是度量空间，对一个上半连续映射f:X→I，我们定义下面的概念：

（2）如果存在x0∈X使得f（x0）＝1，那么称f是正规的；

（3）假设X＝Rn.如果对于任意的α∈（0，1]，[f]α＝{x∈Rn:f（x）≥α}是凸集，那么称f是模糊凸的；

（4）假设X＝Rn.对任意的α∈（0，1]，[f]α星型集，那么称f是模糊星型集.

基于文献[16]的思想，我们能定义下面的概念.如果上半连续函数f:X→I满足上面的（1），那么，我们称f为模糊紧统.用USCC（X，I）表示X的所有模糊紧统.注意当X是紧的，那么，USCC（X，I）＝USC（X，I）.如果上半连续函数 f:Rn→I满足上面的（1）-（3）（相应的（1），（2），（4）），那么我们称 f是一个模糊数（模糊星型数）.设 Y⊂Rn是闭凸集且包含原点O，令K（Y）（SO（Y））表示所有支撑包含在Y中的模糊数（以O为每一个[f]α的星心的模糊星型数）.

对于 f，g∈USCC（X，I），令

end（f）＝{（x，t）∈X×I:t≤f（x）}，send（f）＝end（f）∩（suppf×I）.

使用他们，我们能够在USCC（X，I）上定义三种度量：

D（f，g）＝dH（endf，endg）＜∞，

D'（f，g）＝dH（sendf，sendg）＜∞.

对于p≥1，令

这里 dH是 Hausdorff度量.这样，（USCC（X，I），D），（USCC（Rn），D'），（K（Y），Lp）等是度量空间.

在文献[17-18]中，我们证明了：

定理4.3，令Y是Rn中包含原点的非平凡凸闭子集，那么

（1）（K（Y），D）≈Q⇔（SO（Y），D）≈Q⇔Y 是紧的；

（2）（K（Y），D）≈∑⇔（SO（Y），D）≈∑⇔Y是非紧的.

在文献[19-20]中，刘文娟和张丽丽证明了：

定理4.4.令Y是Rn中包含原点的非平凡凸闭子集，那么（K（Y），D'）≈（SO（y），D'）≈ℓ2.

在文献[21]中，我们证明了：

定理4.5.令Y是Rn中包含原点的非平凡凸闭子集，那么

（1）（K（Y），Lp）≈Q⇔（SO（Y），Lp）≈Q⇔Y 是紧的；

（2）（K（Y），Lp）≈∑⇔（SO（Y），Lp）≈∑⇔Y是非紧的.

我们在文献[22]证明了：

定理4.6.如果X是无限的局部紧非紧可分度量空间，那么

（USCC（X，I），D）≈∑.

张丽丽和Dijkstra在文献[23]证明了：

定理4.7.令X是非平凡的紧的，连通的，局部连通的度量空间或者X＝ℓ2或者X＝Rn.那么

（USCC（X，I），D'）≈ℓ2.

刘文娟等在文献[24]推广了这个结果，证明了下面的定理：

定理4.8.令X是非平凡的，连通的，局部连通的，可分度量空间.那么

（USCC（X，I），D'）≈ℓ2.

下面给出几个与拓扑动力系统有关的函数空间的拓扑结构.设X是紧度量空间，对任意的 f∈C（X，X）和 X 的任意有限开覆盖 U，V，f－1（U）和 U∨V＝{U∩V:U∈U，V∈V}也是X的有限开覆盖.用#（U）表示U的子覆盖的最小个数.那么，我们能够定义f关于覆盖U的拓扑熵为

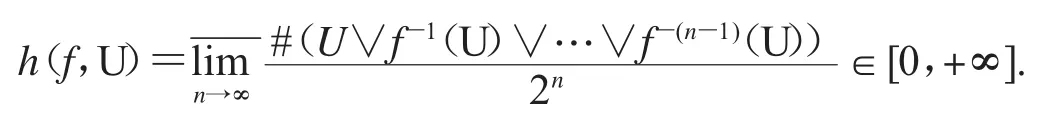
进一步，f的拓扑熵被定义为

对于 α∈[0，∞]，我们使用H＞（aX），H≤（aX）等表示空间C（uX，X）中所有拓扑熵大于α，小于等于α的映射组成的子空间等.

如果对任意的非空开集对U，V，都存在n∈R使得U∩f－（nV）≠，那么我们称f是传递映射.用E（X）表示所有传递映射构成的Cu（X，X）的子空间，表示其闭包.

在文献[25]，作者们证明了：

定理4.9.对任意的α∈[0，＋∞]，我们有

H＞a（I）≈H≥a（I）≈ℓ2.

因此，我们提出下面的问题：

问题4.1.确定空间H＝∞（I），H＜a（I），H＝0（I）的拓扑结构.

在文献[26]，我们证明了：

定理4.10.

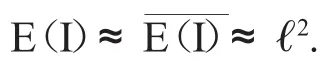
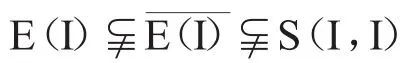
5 非拓扑完备的无限维流形

Toruńiczyk Q-流形特征定理（定理 3.4）和 Toruńiczyk ℓ2-流形特征定理（定理4.1）本质上依赖于这两种流形的完备性.但是，更早的Q中的吸收子并不是拓扑完备的而具有拓扑上的唯一性，即，定理2.2成立.受此启发，人们开始研究一般的Q中的吸收子概念并证明其唯一性.设C是一个拓扑的，闭遗传的空间类，这里，所谓拓扑的是指如果X∈C且X≈Y，那么，Y∈C；所谓闭遗传的是指如果X∈C且Y是X的闭子空间，那么，Y∈C.令

（M0，C）＝{（M，C）∈M0×C:M是紧度量空间且C是M的子空间}.

（i）.Y∈C，

（ii）.Y包含在X的一个Zσ-集中，

（iii）.（X，Y）是（M0，C）-强万有的.

那么，我们称（X，Y）是（M0，C）-吸收子.

设X是可分可度量化空间.如果对任意包含X作为子空间的可分度量空间Y，X都是Y的Fσ-子集，那么，我们称X是绝对Fσ-空间.用Fσ记所有绝对Fσ空间构成的空间类.同理，可以定义绝对 Fσδ-空间和 Fσδ-空间类.可以证明，（M0，Fσ）- 吸收子就是第二节定义的Q中的吸收子，而且定理2.2可以推广为：

定理 5.1.如果（X，A）和（Y，B）都是（M0，C）-吸收子，那么，

（X，A）≈（Y，B）.

1991年，在文献[27]，Dobrowolski等证明了：

定理 5.2.（Dobrowolski-Marciszewski-Mogilski定理）（Q，c0）是（M0，Fσδ）-吸收子.如果X是可数的非离散的度量空间，那么，赋予点态收敛拓扑的函数空间Cp（X，R）同胚于c0.

自2005年以来，我们开始研究一种由超空间拓扑导出的函数空间.对于Tychonoff空间 X 和上半连续函数 f：X→I，end（f）∈Cld（X×I）.对任意的 A∈USC（X，I），令

endA＝{end（f）：f∈A}⊂Cld（X×I）.

于是，作为超空间CldF（X×I）的子空间，我们能够得到函数空间endFA.

下面我们主要考虑 A＝USC（X，I）和 A＝C（X，I）的情况.

在文献[28]，酒井和上原证明了下面的定理：

定理5.3.如果X是无限的紧的度量空间，那么，endFUSC（X，I）≈Q.

相比空间endFUSC（X，I）的拓扑结构问题，我们更关注空间endFC（X，I）和空间对（endFUSC（X，I），endFC（X，I））的拓扑结构问题，这个无疑也更困难.从2005 年到 2018年，我们经过一系列的文章探讨了空间对（endFUSC（X，I），endFC（X，I））的拓扑结构问题.为此，我们在文献[29]中证明了下面的工具性定理：

定理 5.4.令（X，Y，Z）是 3元空间组，那么（X，Y，Z）≈（Q，Σ，c0）的充分必要条件是：

（1）.X≈Q，

（2）.Y可以写成满足下面条件的可数个子集（Yn）n之并：

（a）. 对任意的 n，Yn∈Z（Yn＋1）∩Z（X），

（b）. 对任意的 n，（Yn，Yn∩Z）是强（M0，Fσδ）-万有的，

利用此，最终证明了下面的定理，见文献[29-36]：

定理5.5.设X是度量空间，那么，endFC（X，I）可度量化的充分必要条件是X是局部紧可分可度量化的（后来我们发现这个简单结果是文献[37]中结论（见定理5.5）的推论）.这时有

注意到，上面最后一个结论成立的必要条件是X是可度量化的，因此，上面定理中的所有条件也是必要的.但是，X是可度量化的并不是endFC（X，I）是可度量化的必要条件！事实上，在文献[37]中，McCoy和Ntantu证明了：

定理5.6.如果X是Tychonoff空间，那么，endFC（X，I）是可度量化的充分必要条件是X满足下面的条件：

（i）.X是弱局部紧的，即，对任意的紧集K，存在开集U使得是紧的且K⊂；

（ii）.X是半紧的，即，存在可数紧集族C使得任意的紧集都包含在C的一个成员中；

利用这个结论，我们在2014-2017年证明了下面的定理，见文献[38-41].

定理5.7.设X是k-空间且endFC（X，I）是可度量化的，那么

和定理5.5不同，X是k-空间并不是endFC（X，I）是可度量化的必要条件.事实上，可以证明，当X变化时，可度量化的endFC（X，I）有多达2c个互不同胚的空间（相比之下，如果我们要求X是k-空间，由定理5.7，可度量化的endFC（X，I）仅有可数个互不同胚的空间，非平凡的情况仅有两个）.因此，完全给出endFC（X，I）的拓扑分类是不可能的！

但是，这个课题仍然有很多问题可以研究.例如，令βN是N的Cěch-Stone紧化，q∈βNN，那么，商空间Xq＝（I⊕N∪{q}）/1＝q满足endF（Xq，I）是可度量化的，当然，

Cp（N∪{q}，I）也是可度量化的，我们能提出如下问题：

问题5.1.给出空间Cp（N∪{q}，I）和空间endF（Xq，I）的关系，是否有Cp（N∪{q}，I）≈endF（Xq，I）？

2015年，在文献[42]，杨寒彪等推广了定理5.5，得到了函数空间的值域为dendrite时的对同胚性质，证明了下面的定理：

定理5.8.令X是仅包含有限孤立点的紧可度量化空间，Y是dendrite（不包含闭环的皮亚诺连续统）.则：

（endFUSC（X，Y），endFC（X，Y））≈（Q，c0）.

2020年在文献[43]，杨寒彪等推广了定理5.8，得到了函数空间的值域为树并且其赋予的方向与定理5.8相反时候的同胚性质，证明了下面的结论：

定理 5.9.令 X 是皮亚诺连续统，Y 是包含 n 个分支{S1，S2，···，Sn}的树.则：

这里CUP（Si）＝{f∈C（X，T）:maxf（X）∈Si}，这里endFCUP（Si）是可缩空间.

越野在文献[44]中应用文献[35]的思想证明了下面的结论：