IRVEA：一种改进角度惩罚距离的RVEA算法

郭华，韦伟，谢承旺,2，潘嘉敏，程文旗，谢子若

IRVEA：一种改进角度惩罚距离的RVEA算法

郭华1，韦伟1，谢承旺1,2，潘嘉敏1，程文旗1，谢子若3

（1. 南宁师范大学 计算机与信息工程学院，广西 南宁 530000；2. 华南师范大学 数据科学与工程学院，广东 汕尾 516600；3. 华东交通大学 软件学院，江西 南昌 330013）

多目标和高维多目标进化算法致力于平衡收敛性和多样性。经典的RVEA算法利用角度惩罚距离方法平衡收敛性与多样性，但它仍存在不足，从而对算法的性能产生不利影响。课题组提出一种改进的角度惩罚距离方法IAPD以更好地平衡算法的收敛性和多样性，并将IAPD策略嵌入RVEA中，以取代原始的APD方法，设计了一种改进角度惩罚距离的RVEA算法，即IRVEA。IRVEA与其他三种经典的高维多目标进化算法一同在3-、5-、8-和10-目标的WFG1～WFG6测试问题上进行IGD性能测试，结果表明：该算法在平衡收敛性和多样性上具有显著优势。由此表明IRVEA算法是一种有前途的高维多目标进化算法。

高维多目标优化；进化算法；改进角度惩罚距离；参考向量

1 引言

在科学计算与工程实践中存在大量需要同时优化多个目标的问题，它们通常被称为多目标优化问题[1]（multi-objetive optimization problem，MOP）。MOP各目标之间往往相互冲突，改善其中一个目标将导致其他一个或多个目标性能的恶化。因此MOP一般不存在单个最优化能同时优化所有目标，其求解结果往往是一组折中解，即Pareto解集或非劣解集[2]。

进化算法（evolutionary algorithm，EA）是一类基于群体搜索的启发式方法，它运行一次可获得一组解，而且它具有内在并行性，可显著地改善算法的搜索性能。自20世纪80年代以来，研究者基于不同的背景和视角陆续提出了一些用于求解MOP的进化算法，即多目标进化算法[3–5]（multi-objective evolutionary algorithm，MOEA）。根据这些MOEA算法的主要特征可将它们粗略地分为基于支配关系、基于分解和基于指标等三种主要的类型，而且，这些算法在求解目标数较少的MOP（即含有2至3个目标）时具有较好的性能，并取得了令人鼓舞的结果[6]。

随着社会经济的发展，现实中不断涌现出需要同时优化更多目标的问题，即高维多目标优化问题[7]（many-objective optimization problem，MaOP）。这些MaOP问题的目标数通常不少于4。MaOP的出现给基于Pareto支配的MOEA算法带来了巨大挑战，其原因在于：1）Pareto最优性无法有效区分高维目标空间中解个体的优劣，使得进化算法的选择压力骤降，难以驱使种群逼近Pareto前沿[8]；2）高维目标空间中解个体分布稀疏，它们产生的后代与双亲间的差异较大，使得进化算法的变化算子面临失效的困境[9]；3）在高维目标空间中为保持种群的多样性需评估解个体的邻域拥挤度，而这需要巨大的计算开销[10–11]，因此如何有效保持高维目标种群的多样性亦具挑战性。

鉴于这些困难和挑战，Deb等[10]利用参考点的方法在高维目标空间产生一组均匀分布的参考点以引导种群搜索，期望获得一组均匀分布的Pareto近似解。在此基础上，Cheng等[12]提出一种参考向量引导的高维多目标进化算法RVEA（reference vector guided evolutionary algorithm，RVEA），该算法的关键在于利用角度惩罚距离（angle penalized distance，APD）的标量化方法动态平衡高维目标优化的收敛性和多样性。然而，APD方法并不能有效地平衡算法的收敛性和多样性，其原因在于：在进化搜索的前期，APD强调种群的收敛性而牺牲了多样性；而在搜索的后期，APD为了维护种群的多样性而忽视了收敛性。基于此，为有效平衡高维多目标进化算法的收敛性和多样性，这里提出一种改进的基于参考向量的高维多目标进化算法IRVEA（improved reference vector guided evolutionary algorithm，IRVEA）。IRVEA算法的主要创新在于：提出一种改进的角度惩罚距离方法IAPD（improved angle penalized distance，IAPD），它能有效地平衡高维目标种群的收敛性和多样性以获得高质量的解集。IRVEA与三种高效的高维多目标进化算法，即RVEA[12]、NSGA-Ⅲ[10]和MOEA/DD[13]，一同在WFG[14]系列测试问题上进行性能实验，结果表明IRVEA算法具有显著较优的收敛性与多样性之综合性能。

2 预备知识

2.1 多目标优化问题的定义

为不失一般性，一个最小化MOP可表示如下：

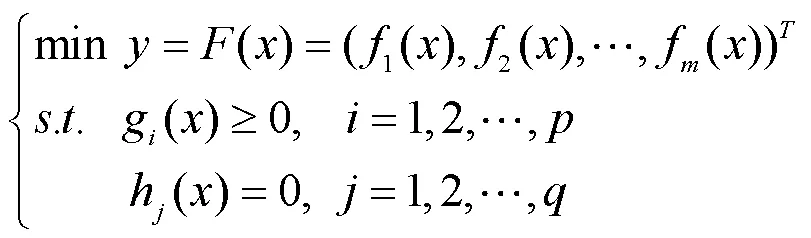
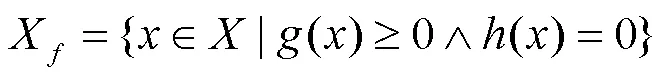
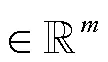
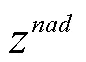
2.2 角度惩罚距离APD

经典的RVEA算法利用角度惩罚距离APD方法动态平衡高维目标优化的收敛性和多样性。APD利用解点与理想点之间的欧式距离度量收敛性，用解向量（解点）与参考向量之间的锐角来度量多样性。相比于基于惩罚的边界相交法（penalty-based boundary intersection, PBI）采用欧式距离度量多样性，APD则是利用基于角度的距离度量方法，它一方面更易于进行规范化，另一方面在优化目标数上更易于扩展[15]，而这对高维目标优化显得尤为重要。

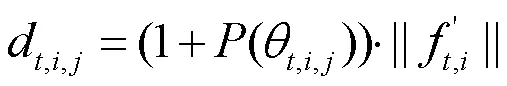
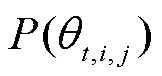
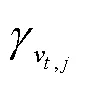
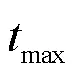
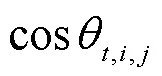
3 改进角度拥挤距离的RVEA算法

3.1 APD方法的缺陷

由于APD方法在算法搜索的前期强调收敛性而忽视多样性，在后期重视多样性而忽略了收敛性，因而在有效平衡高维目标算法的收敛性和多样性方面存在不足，下面通过图1说明存在的问题。

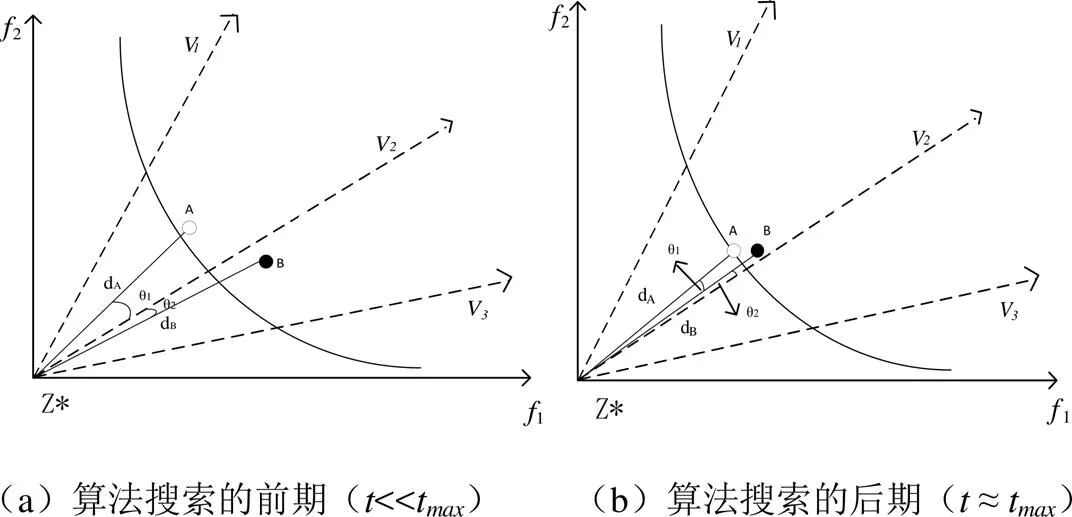
图1 APD方法存在的不足

如图1（a）所示，个体A和B均与参考向量2进行了关联，并有A2成立。如果利用APD机制选择个体，由于前期APD机制强调收敛性而忽视多样性，则个体A将被选中进入下一代。但需看到，个体A和B到原点的距离相差很小，而它们与参考向量的夹角1和2相差却较大。综合来看，个体B更应该保留至下一代。当算法搜索后期，种群已较稳定地逼近于Pareto前沿，此时各个体与原点之间的距离（即收敛性）相差不大。如图1（b）所示，个体A和B与参考向量2进行了关联，并有A2成立。如果利用APD机制择优个体，由于搜索后期APD更侧重多样性，因此个体B被选中进入下一代。但是，个体A实际上是支配个体B的，因此选中个体A而非个体B则更能促进收敛。换言之，在搜索后期，APD机制可能会淘汰Pareto非劣解而选中被支配解，因而算法性能存在下降风险。

3.2 改进的角度惩罚距离方法

针对3.1小节中APD方法存在的不足，这里提出一种改进的角度惩罚距离方法（improved angle penalized distance, IAPD）。以下给出IAPD方法的数学描述，如公式（6）所示：

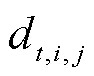
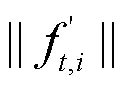
3.3 IRVEA算法流程

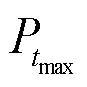
算法1：IRVEA算法流程

输入：最大进化代数t，一组均匀分布的单位权值向量0= {0,1,0,2, …,0,N}。

步骤1：随机产生规模为的初始代种群0；

步骤2：WHILE<t

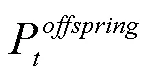
步骤7：环境选择:P+1=Environmental-selection(P，V)；

步骤8：参考向量的自适应调整:V+1= Reference-vector-adaption(，P+1，V，0)；

步骤9：=+1；

步骤10：END WHILE；

算法1的第7步执行环境选择涉及4个主要步骤，分别是：1）种群的划分，即将个体的目标值向量转换后计算各个体与参考向量之间的角度，以确定个体所属的子种群（关联的参考向量）；2）IAPD选择策略，即分别计算个体的IAPD值，并选择值最小的个体进入下一代；3）采用角度向量精英保留策略，保持种群规模不变。需要指出的是，这里的环境选择策略与RVEA的环境选择策略类似，所不同的是，这里是通过计算IAPD值而非APD值来择优个体。考虑篇幅限制，算法1的环境选择策略省去，读者可参阅文献[12]。

4 实验与分析

为验证IRVEA算法的性能，这里将它与当前主流的高维多目标进化算法，即RVEA、NSGA-Ⅲ和MOEA/DD一同在3-、5-、8-和10-目标的WFG[14]系列测试问题进行IGD[17]性能测试，各算法在每个测试例上均独立执行20次获得IGD指标的均值和方差，并利用显著水平为0.05的Wilcoxon秩和检验来分析各算法获得近似解集的性能在统计意义上的差异，以获得有说服力的结论。

4.1 测试问题

实验利用WFG1～WFG6测试问题作为基准测试函数考察算法的性能。采用WFG系列函数的原因是：1）该系列测试问题的目标数和决策变量数是可扩展的；2）WFG系列问题的真实PF是已知的，而且PF具有不同的难度特征，它们对算法逼近真实PF构成了巨大挑战。表1列出了WFG系列测试问题的难度特征。

表1 WFG1～WFFG6测试问题的难度特征

4.2 性能指标

为了综合评估算法的收敛性和多样性，本文采用反转世代距离（inverted generational distance，IGD）。IGD指标可以同时度量近似解集的收敛性和多样性，原因在于：实验所采用的测试问题的真实PF是已知的，通过在真实PF上均匀采样多样性的点，计算这些采样点到近似Pareto解点之间的距离，既能反映解集的收敛性又能反映多样性。一般而言，IGD指标值越小，表示近似解集的收敛性和多样性越好。假设P是MOP问题真实PF的代表解集，IGD性能指标可利用公式（7）进行计算：

4.3 实验结果与分析

为了验证IRVEA算法的有效性，这里将本文算法与3种具有代表性的高维多目标进化算法，即NSGA-Ⅲ，RVEA，MOEA/DD一同在WFG1～WFG6测试函数上进行了IGD指标性能比较。实验中考察的目标数目分别为3、5、8和10个目标，其分别对应的种群规模设为92、212、156和276。

表2给出了IRVEA、RVEA、NSGA-Ⅲ和MOEA/DD四种算法在WFG1～WFG6共24个测试实例上的IGD均值与方差，以及它们的优劣对比。表现最优的IGD值用粗体标注。从表2可以看出，IRVEA、RVEA、NSGA-III和MOEA/DD分别获得了11、6、7和0个最优的IGD均值。从表2的Wilcoxon秩和检验的结果可知，IRVEA算法的净胜得分（劣于的数目减去优于的数目即为净胜得分）相比于RVEA、NSGA-Ⅲ、MOEA/DD算法，分别为7、9和20。由此可见，IRVEA相比其他三种对比算法，它在求解WFG系列测试函数具有显著较优的性能。究其原因，IRVEA中的改进的角度惩罚距离能够更好地平衡收敛性与多样性，因而能够获得相对较好的解题性能。

表2 四种算法在WFG系列测试函数上的IGD均值与方差

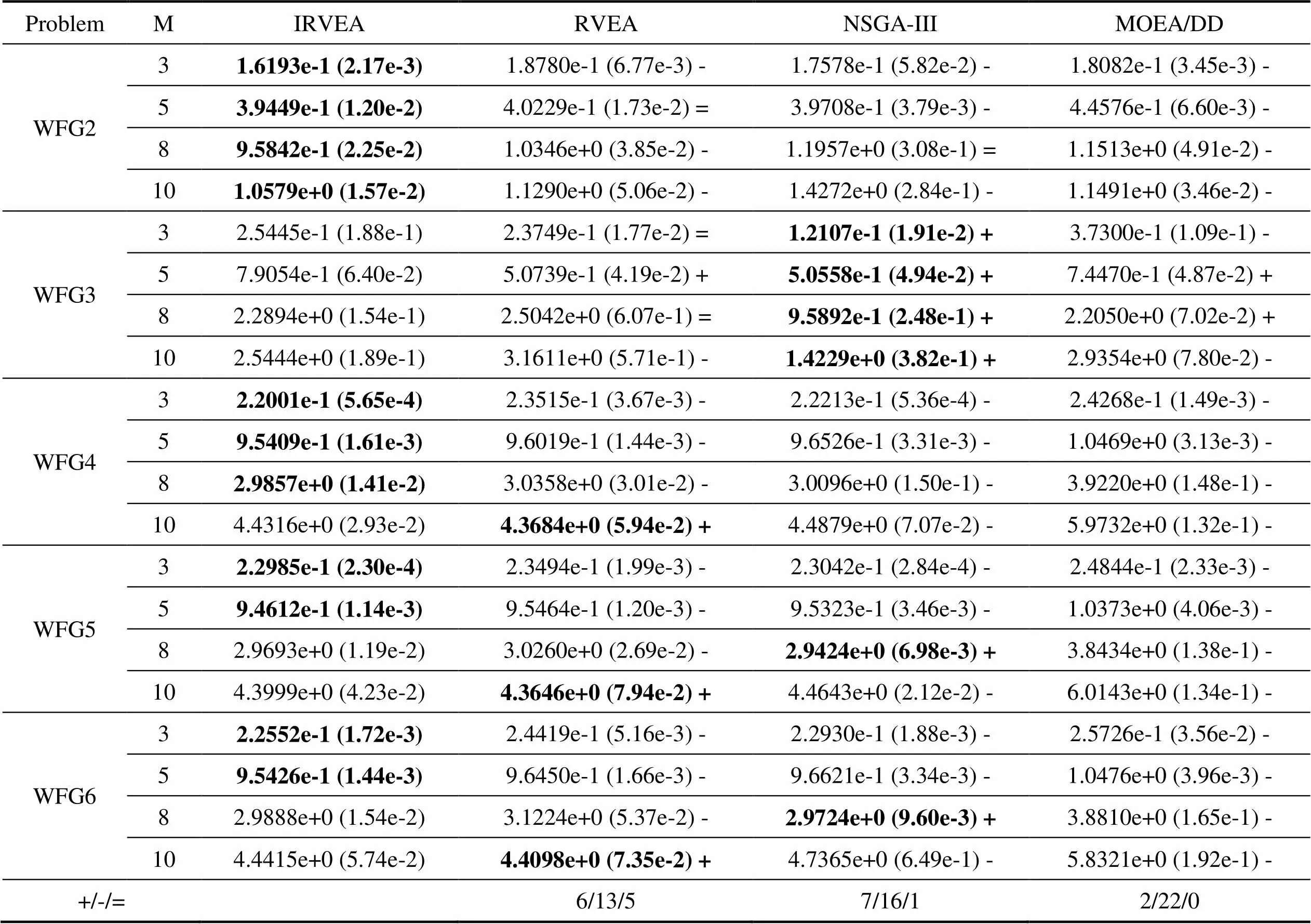
表2 四种算法在WFG系列测试函数上的IGD均值与方差（续）

注：‘+’、‘-’和‘=’分别表示该结果显著地优于、劣于和统计上无差别于IRVEA算法

4 结论

课题组针对经典RVEA算法中基于APD的不足，提出一种改进APD的方法，即IAPD。随后将该算子嵌入到RVEA算法中以替代原有的APD方法，并由此构造一种改进的RVEA算法，即IRVEA。新算法与三种经典的高维多目标进化算法一同在WFG1～WFG6测试问题上进行IGD性能指标测试，结果表明，本文算法能够更好地平衡高维目标空间中解群的收敛性与多样性，它将是一种有前途的高维多目标优化器。未来将利用一些更加复杂的MaOP检验本文算法的性能,并利用该算法求解现实应用中的一些MaOP。

[1] DEB K. Multi-objective optimization using evolutionary algorithms: an introduction[M]// Multi-objective evolutionary optimization for product design and manufacturing. Springer, London, 2011: 3–34.

[2] ZHOU A, QU B Y, LI H, et al. Multiobjective evolutionary algorithms: A survey of the state of the art[J]. Swarm and evolutionary computation, 2011, 1(1): 32–49.

[3] 谢承旺, 王志杰, 夏学文.应用档案精英学习和反向学习的多目标进化算法[J]. 计算机学报, 2017, 40(3):757–772.

[4] MA H, SHEN S, YU M, et al. Multi-population techniques in nature inspired optimization algorithms: A comprehensive survey[J]. Swarm and evolutionary computation, 2019, 44: 365–387.

[5] Falcón-Cardona J G, Coello C A C. Indicator-based multi-objective evolutionary algorithms: A comprehensive survey[J]. ACM computing surveys (CSUR), 2020, 53(2): 1–35.

[6] TIAN Y, CHENG R, ZHANG X, et al. A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2018, 23(2): 331–345.

[7] ISHIBUCHI H, AKEDO N, NOJIMA Y. Behavior of multi-objective evolutionary algorithms on many-objective knapsack problems[J]. IEEE Transactions on Evolutionary Computation, 2014, 19(2): 264–283.

[8] TIAN Y, WANG H, ZHANG X, et al. Effectiveness and efficiency of non-dominated sorting for evolutionary multi-and many-objective optimization[J]. Complex & Intelligent Systems, 2017, 3(4): 247–263.

[9] Purshouse R C, FLEMING P J. On the evolutionary optimization of many conflicting objectives[J]. IEEE transactions on evolutionary computation, 2007, 11(6): 770–784.

[10] DEB K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based non-dominated sorting approach, part I: solving problems with box constraints[J]. IEEE transactions on evolutionary computation, 2013, 18(4): 577–601.

[11] JAIN H, DEB K. An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach, part II: Handling constraints and extending to an adaptive approach[J]. IEEE Transactions on evolutionary computation, 2013, 18(4): 602–622.

[12] CHENG R, JIN Y, OLHOFER M, et al. A reference vector guided evolutionary algorithm for many-objective optimization[J]. IEEE transactions on evolutionary Computation, 2016, 20(5): 773–791.

[13] LI K, DEB K, ZHANG Q, et al. An evolutionary many-objective optimization algorithm based on dominance and decomposition[J]. IEEE Transactions on Evolutionary Computation, 2014, 19(5): 694–716.

[14] HUBAND S, HINGSTON P, BARONE L, et al. A review of multi-objective test problems and a scalable test problem toolkit[J]. IEEE transactions on evolutionary computation, 2006, 10(5): 477-506.

[15] 谢承旺, 李凯, 廖国勇.一种带差分局部搜索的改进型NSGA2算法[J]. 计算机科学, 2013, 40(10):235–238+273.

[16] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182–197.

[17] ZITZLER E, THIELE L, LAUMANNS M, et al. Performance assessment of multi-objective optimizers: An analysis and review[J]. IEEE Transactions on evolutionary computation, 2003, 7(2): 117–132.

IRVEA: A New RVEA Approach with Improved Angle Penalty Distance

GUO Hua1,WEI Wei1, XIE Cheng-wang1,2, PAN Jia-min1,CHENG Wen-qi1, XIE Zi-ruo3

（1. School of Computer and Information Engineering, Nanning Normal University, Nanning Guangxi 530000; 2.School of Data Science and Engineering, South China Normal University, Shanwei, Guangdong 516600; 3. School of Software, East China Jiaotong University, Nanchang, Jiangxi 330013, China）

Multi-objective and many-objective evolutionary algorithms are devoted to balance convergence and diversity. The classical RVEA approach uses the angle penalty distance method to balance the convergence and diversity, but it still has shortcomings, which results in the adverse impact on the performance. An improved angle penalty distance method, that is IAPD, is proposed to better balance the convergence and diversity, and the IAPD strategy is embedded in the original RVEA to replace APD method, then the improved RVEA, that is IRVEA, is designed to solve MaOPs effectively. The IRVEA is compared with the other three typical many-objective evolutionary algorithms based on IGD indicator on WFG1 to WFG6 with 3-, 5-, 8-, and 10- objectives, respectively. The empirical results show that the proposed IRVEA has significantly advantageous over the peer algorithms in terms of convergence and diversity. Therefore, the IRVEA is a promising solution for MaOPs.

many-objective optimization problems; evolutionary algorithm; improved angle penalty distance; many-objective evolutionary algorithm; reference vector

TP181

A

2095-9249（2021）06-0062-06

2021-10-10

国家自然科学基金（61763010）；广西自然科学基金（2021GXNSFAA075011）；广西研究生教育创新计划项目（YCSW2020194）

郭华（1996—），女，甘肃陇南人，硕士研究生，研究方向：智能计算和多目标优化。

谢承旺（1974—），男，湖北武汉人，教授，博士，研究方向：智能计算，E-mail: chengwangxie@m.scnu.edu.cn

〔责任编校：陈楠楠〕