基于用户满意度的电动汽车无序充电影响研究

谢远德，邓沙丽

基于用户满意度的电动汽车无序充电影响研究

谢远德，邓沙丽

（萍乡学院 工程与管理学院，江西 萍乡 337000）

为了研究电动汽车大规模无序充电对电网的影响，首先，对用户出行时刻、出行距离进行分析；其次，根据用户充电量引入超时惩罚费用概念，计算所有用户充电费用；最后，以用户充电满意度最大为目标，充电时间、充电功率、用户需求等为约束条件，建立单目标非线性规划模型，并对某小区仿真。结果表明，无序充电下，电网最大负荷达到了2051.5KVA，出现了过载、超负荷运行、峰上加峰等不良情况，不利于电网运行安全稳定性；峰谷差高达1228.35KVA，峰谷差率比基础负荷峰谷差率增加了5.38%，达到59.88%。

电动汽车；无序充电；用户满意度；非线性规划

传统汽车的动力能源主要来源于汽油燃烧，这不仅会加剧我国化石能源短缺的窘迫现状，还会产生污染尾气，背离了我国“绿色环保”发展理念[1–2]。而电动汽车作为一种新兴产业，以电产能，具有“无污染、低噪声、节能环保”的特点，它的出现，有效地缓解了环境能源问题[3–4]。随着电动汽车数量持续增长，充电需求也在不断增加，这无疑会给电网带来巨大的冲击[5]，不少学者对该问题展开了研究[6–10]。

郝越[11]为分析不同功率的电动汽车无序充电过程，采用多项式拟合论证了充电量与时间的关系，并基于拉格朗日乘数法建立优化模型；郑晶晶[12]等对用户行为特性进行分析，建立了电动汽车无序充电数学模型，并运用蒙特卡洛法模拟仿真，但该模型考虑的因素过于单一，存在一定局限性；杨昕然等[13]基于复杂网络理论，以城市交通网为约束，评估了电动汽车在恶劣充电场景下无序充电对电网的影响；罗庆[14]在IEEE33节点算例系统的基础上，考虑充电需求的增加，研究了电动汽车随机充电对电网的影响，但该方法只考虑了电动汽车渗透率；徐佳夫[15]等在 Simulink平台搭建住宅区充电站模型，根据无序充电下的负荷分布和车载机模型，研究了不同时刻电网的谐波电流；何若太等[16]为分析无序充电时空特性，建立了基于出行链下电动汽车出行的时空模型，提出蒙特卡罗法模拟负荷曲线；王利利等[17]充分考虑电动汽车接入电网时的影响和效益，针对不同的充电策略，提出了各样的评估方法并建立了相应的数学模型，进行了实验仿真；付坤[18]总结电动汽车的日均用电需求，并分析用户充电行为的时空特性，得到了电动汽车充电负荷的时空分布曲线，但未将时间细分，导致误差较大；周思宇[19]对电动汽车无序充电负荷影响因素进行研究，并采用蒙特卡洛对规划区域进行负荷预测，从不同角度验证了无序充电对配电网的不良影响；刘阿理[20]基于现有统计数据，分析了电动汽车耗电量的影响因素，建立了充电负荷模型，但容易出现过拟合现象。

基于电动汽车用户到达充电站进行充电是相互独立的，具有较大的随机性、灵活性和不确定性的特点，将一天时间平均划分；从电动汽车用户行为的角度，根据用户充电量引入了超时惩罚费用概念，同时以用户充电满意度最大为优化目标，以充电功率、充电时长等为约束条件，建立单目标非线性规划模型，对电动汽车无序充电对电网负荷的影响进行研究。

1 用户行为分析

电动汽车用户日出行特征对充电需求有着较大的影响。图1为电动汽车用户出行时刻分布规律图，该图反映了用户每天开始出行时刻的分布规律以及出行比例。

图1 用户出行开始时刻分布规律

用户日出行距离的分布规律如图2所示，该图准确地反映了私家电动汽车用户出行不同日行驶里程分布。

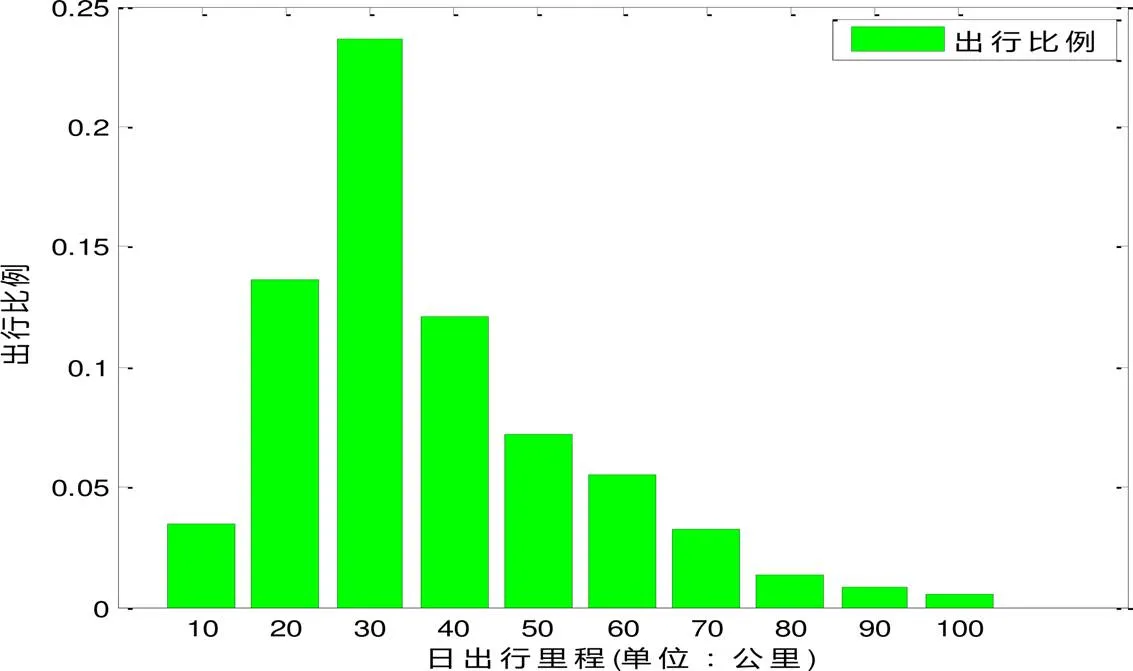
图2 电动汽车日出行距离分布规律

2 电动汽车无序充电研究

由于电动汽车在一天时间内任何时刻都有可能接入电网，为了准确地得到电动汽车的初始荷电状态和接入电网时间，考虑将一天时间平均分成96个时段，每个时段均为15min，所有时段组成了一个集合，在每个时段的开始时刻更新电动汽车的接入信息，其中主要包括电动汽车数量、每辆电动汽车的初始荷电状态、用户电动汽车荷电状态期望值以及电池容量等信息。具体如图3所示：

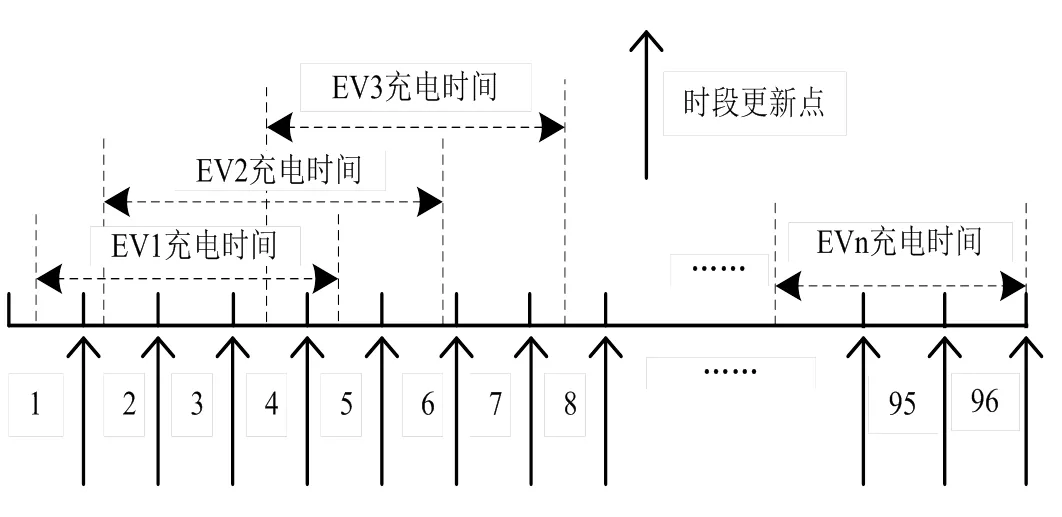
图3 时段更新示意图

电动汽车用户选择是否充电与电动汽车的初始荷电状态（State of Charge，SOC）有关，当电动汽车电池的初始荷电状态不满足出行需求或者由出行剩余里程引起心理焦虑时，用户会选择充电，反之则不充电。假设每个电动汽车用户都有一个初始荷电状态以及充电结束的荷电状态期望值，初始荷电状态就是用户的荷电状态期望值与用户下一次出行所需电能的差值，即：

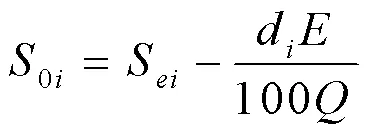
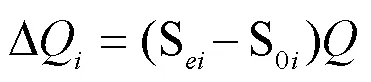
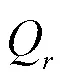
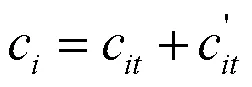
由于用户在达到阈值时间内只需要支付期望充电量的费用，令4表示充电电价，因此得到此费用为：

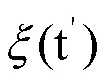
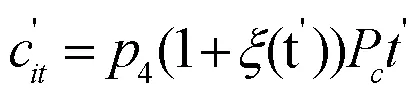
惩罚系数主要与超过阈值充电量的充电时长有关，当该时间为0时，表示用户充电未超时，此时惩罚系数也为0；随着此时间不断变长，惩罚系数也会随之不断增大，因此，不妨定义惩罚系数与超时长成正比的关系，即：

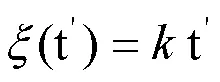
综上所述，第电动汽车用户选择充电产生的费用为：

为了得到无序集中充电下一天内所有用户充电的总费用0，将一天内各电动汽车用户的充电费用累加起来，则有：

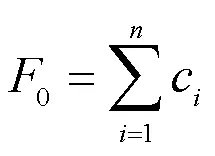
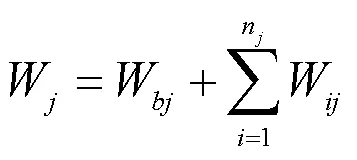
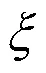
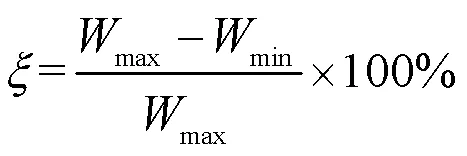
3 用户充电满意度

居民用户一般都有固定的生活作息规律，他们更愿意按照自己的意愿选择充电时间。因此，在无序充电模式下，只考虑EV用户充电满意度，即以平均每个用户满意度最大为优化目标建立数学模型。

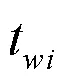
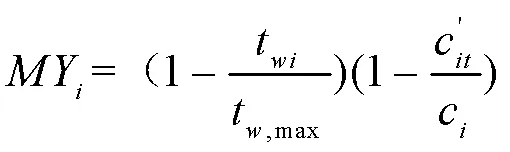
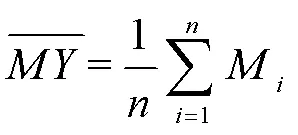
3.1 约束条件

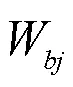
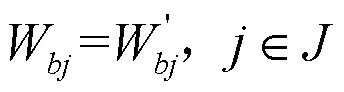
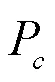
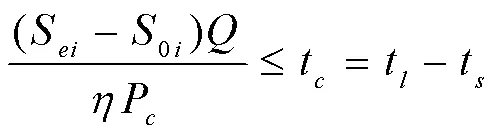
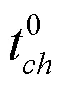
选择充电的电动汽车用户在结束充电时的真实电量应该不小于用户的荷电状态期望值。显然，充电量不可能大于电池容量，即：

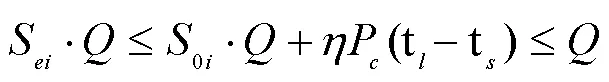
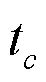
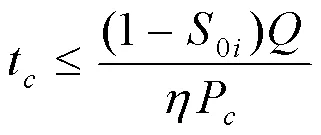
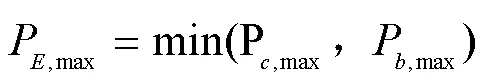
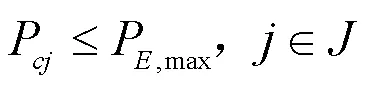
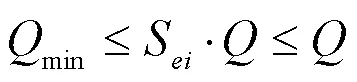
无论是何时何地何种情况，任意时段正在充电的电动汽车数量都不得大于电动汽车总数量，既满足：

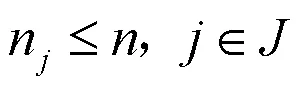
由式（12）∽（21），得到电动汽车无序充电下的数学优化模型为：

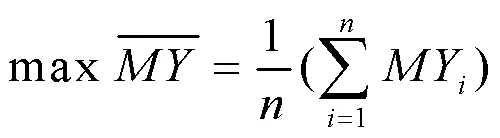
3.2 算法实现

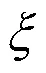
4 实例仿真

某小区住户数量为350户，占地面积约为25000m2，由一台2000KVA的配电变压器供电，车位配比为1:1.5，该小区最大负载率为80%（负载率是指该变压器实际承担的负荷与电网容量之比，用于反映变压器的承受能力，其中变压器经济运行最佳上限为75%∽80%）。一般情况下，住宅小区内的居民都有一定的作息规律。为了方便清楚地验证电动汽车接入电网充电时的影响，只考虑小区居民正常生活的基本用电状况和电动汽车充电所需的电量，其他形式的用电暂不考虑。

根据上述内容设定的仿真环境，对该居民小区的典型日用电状况进行分析，仿真结果如图4所示：

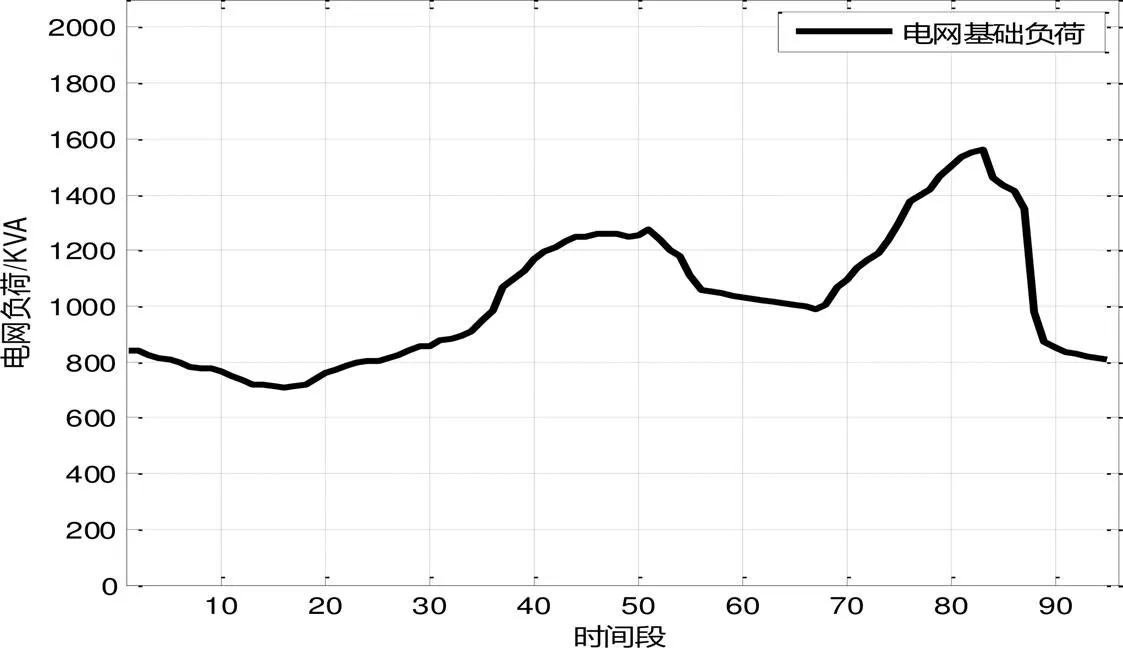
图4 电网基础负荷曲线图

从图4可知，若配电变压器只需提供满足居民日常生活用电量，在任意时刻都不会出现过载、超负荷的情况。从整体来看，电网负荷曲线出现了一次低谷时段和两次高峰时段。其中，在夜间11:00到早上7:00左右，居民处于睡眠状态，用电少，电网负荷处于低谷，而到了中午11:30到13:00左右和晚上19:00到22:00左右，居民用电量增加，电网负荷出现了高峰。尤其是晚上，除了一些家用电器的使用，居民需使用电灯、热水器等电器，再加上公共用电基础设施，导致电网负荷迅速上升，接近小区电网最大负载率。

在一日一充或多充的充电模式下，为了满足居民用户的充电需求，在每个停车位都配置充电桩。在用户其他用电负荷无干预的情况下，仿真小区居民无序充电结果如图5所示：

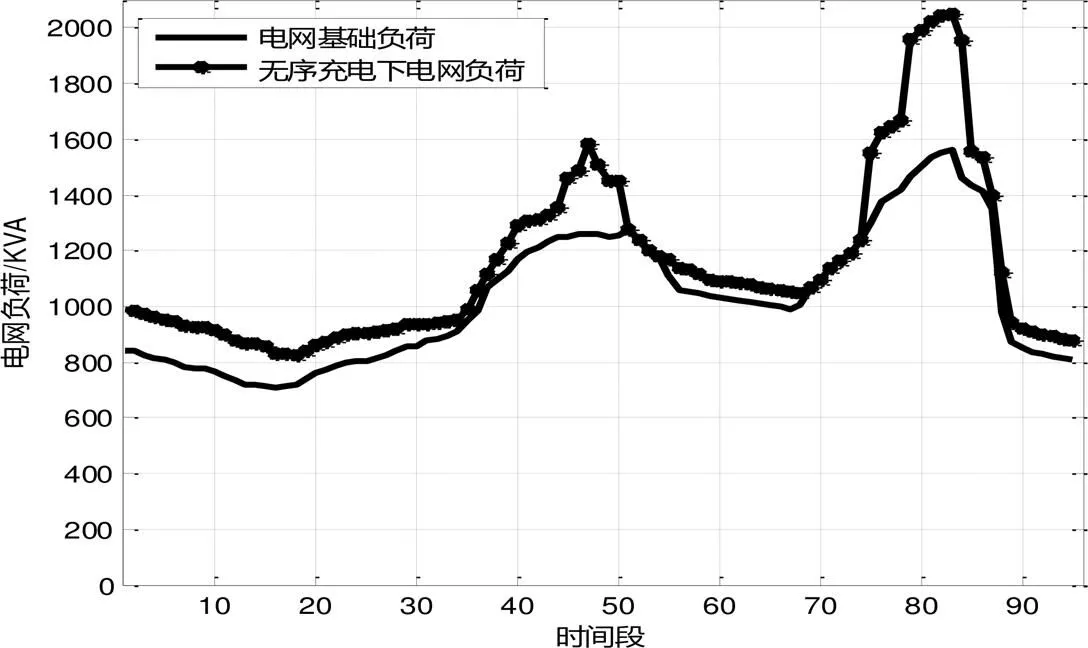
图5 无序充电下电网负荷

从图5中可知，若用户完全按照自己的生活作息规律选择充电，会导致峰上加峰的现象，甚至出现了过载、超负荷，影响了用电质量及电网安全运行。从整体看，电网负荷曲线在相同的时间出现了一次低谷时段和两次高峰时段。在低谷时段，极少用户选择充电，导致用电少，电网负荷曲线增加不明显；而在中午和晚上，电网负荷曲线明显增加，说明选择充电的用户多，尤其是晚上19:00—22:00，电网实际负荷已经在短时间内超过了电网最大负荷，这是因为经过一天的使用后，电动汽车剩余电量不足以满足用户下一次的出行需求，因此，大部分用户都会选择充电。

表1 无序充电下峰谷差率及费用

从表1可知，小区基础用电最小负荷仅为710.3KVA，而最大负荷达到1561.1KVA，临近该小区的最大负载率，但未超过配电变压器的范围，能够满足居民日常生活用电；小区电网基础负荷峰谷差为850.8KVA，峰谷差率为54.5%；接入电动汽车充电后，由于EV用户按照自己的生活作息习惯选择充电时间，只有少部分充电时间长的用户才会选择夜间充电，导致电网最小负荷偏低，只有823.15KVA，而最大负荷达到了2051.5KVA，出现了超负荷、峰上加峰等负面情况，不利于电网运行安全稳定性；峰谷差高达1228.35KVA，峰谷差率也有所上升，达到59.88%，比基础负荷峰谷差率增加了5.38%，电动汽车无序充电费用为2118元。

5 结论

为研究电动汽车无序充电对电网系统的影响，首先从用户出发时刻以及出行距离等特征进行分析，其次，通过用户荷电状态期望值与电动汽车的初始荷电状态，计算得到用户充电量，根据用户充电量引入了超时惩罚费用概念，计算得到电动汽车无序充电下的总费用，以电动汽车用户的人均满意度最大为目标，充电时长、充电功率、用户需求等为约束条件，建立了约束条件下的单目标数学优化模型，并通过实例仿真分析验证了模型的准确性。结果表明，在无序充电模式下，电动汽车接入电网会导致峰上加峰、峰谷差率变大的现象，甚至出现了过载、超负荷等不良情况，无法保障用电质量，对电网运行造成了负面影响。后续工作可以充分考虑用户侧和电网侧，提出实现用户-电网双赢局面的有序充电策略。

[1] 黄小晴. 基于需求的电动汽车充电站网络优化布局[D]. 南昌: 南昌航空大学, 2019: 50.

[2] 虞小辉. 计及多能互补的电动汽车充电站优化配置及规划研究[D]. 南京: 南京邮电大学, 2020: 84.

[3] 梁梦梦. 基于用户满意度的电动汽车充电站规划研究[D].成都: 西南交通大学, 2020: 80.

[4] 叶露. 基于双层规划的电动汽车充电站选址模型[D]. 成都: 西南交通大学, 2020: 83.

[5] 王睿. 电动汽车充电负荷预测方法及有序充电策略研究[D]. 北京: 北京邮电大学, 2020: 63.

[6] Zhang S, Zhu J, Wang B, et al. Multi-objective optimization charging strategy for plug-in electric vehicles based on dynamic Time-of-use price[J]. Power system protection & control, 2017, 2（1）: 28-34.

[7] Sun X, Wang W, Su S, et al. Coordinated charging strategy for electric vehicles based on time-of-use price[J]. Automation of electric power systems, 2013, 37(1): 191–195.

[8] Sun Qiang, Xu Fangyuan, Tang Jia et al. Study on modeling of aggregated charging load of electric vehicles and control strategy by adjusting capacity boundaries based on demand response[J]. Power system technology, 2016, 40（9）: 2638–2645.

[9] 周步祥, 何飞宇, 魏金萧, 等. 基于实时最优恒定功率的电动汽车有序充电策略[J]. 电测与仪表, 2021, 58（12）: 18–23.

[10]汪天允, 张浩. 基于人工鱼群算法的电动汽车优化充电策略[J/OL]. 电测与仪表, 2021（1）: 1–6[2022-03-02].http://kns.cnki.net/kcms/detail/23.1202.th.20210118.0959.002.html.

[11] 郝越. 电动汽车无序充电的影响分析[J]. 通信电源技术, 2019, 36(11): 94–96+100.

[12] 郑晶晶, 闫志杰, 李伟, 等. 基于蒙特卡洛法的电动汽车无序充电对电网的影响分析[J]. 电气传动自动化, 2019, 41（5）: 1–5.

[13] 杨昕然, 吕林, 向月, 等. “车-路-网”耦合下电动汽车恶劣充电场景及其对城市配电网电压稳定性影响[J]. 电力自动化设备, 2019, 39（10）: 102–108+122.

[14] 罗庆. 电动汽车充电对电网的影响及有序充电研究[D].杭州: 浙江大学, 2016: 74.

[15] 徐佳夫, 王旭红, 李浩, 等. 无序充电模式下电动汽车对住宅区配电网谐波影响研究[J]. 电力科学与技术学报, 2019, 34（2）: 61–67.

[16] 何若太, 刘澄, 王颖, 等. 基于出行链的电动汽车无序充电对配电网影响的时空特性分析[J]. 电气应用, 2018, 37（21）: 29–35.

[17] 王利利, 李猛, 全少理, 等.电动汽车的主动管理及其对配网的影响建模[J]. 电测与仪表, 2017, 54（3）:60–66.

[18] 付坤. 电动汽车的行为模拟及充放电调度策略研究[D].济南: 山东大学, 2021: 95.

[19] 周思宇. 电动汽车充电负荷对配电网的影响及有序充放电策略[D]. 徐州: 中国矿业大学, 2020: 87.

[20] 刘阿理. 居民区电动汽车有序充电策略及其对配电网的影响研究[D]. 成都: 西南交通大学, 2020: 75

Research on the Impact of Disorderly Charging of Electric Vehicles Based on User Satisfaction

XIE Yuan-de, DENG Sha-li

(School of Engineering and Management, Pingxiang University, Pingxiang, Jiangxi 337000, China)

The purpose is to study the impact of large-scale disorderly charging of electric vehicles on the power grid. First, the user’s travel time and travel distance is analyzed; Secondly, the concept of overtime penalty fee is introduced based on the user’s charging amount to calculate all user charging fees; Finally, a single-objective nonlinear programming model is established and simulated with the maximum user charging satisfaction as the goal and charging time, charging power and user demand as the constraints. The results show that under disorderly charging, the maximum load of the grid reaches 2051.5 KVA, and there are undesirable situations such as overcharge, overload operation, and peak on peak, which are not conducive to the safety and stability of grid operation; the peak-to-valley difference is as high as 1228.35 KVA, and the peak-to-valley difference rate increases by 5.38% to 59.88% compared with the base load peak-to-valley difference rate.

electric vehicles; disorderly charging; user satisfaction; nonlinear planning

U491.8

A

2095-9249（2021）06-0018-06

2021-12-07

国家自然科学基金项目（52062038）；江西省教育厅科学技术研究项目（GJJ212717）；江西省研究生创新专项资金项目（YC2019-S344）

谢远德（1994—），男，江西赣州人，助教，硕士，研究方向：优化与建模、电动汽车。

〔责任编校：陈楠楠〕