开放式教学模式探索

钟顺

摘 要 在教学过程中，以“科氏力实验系统”为教学案例，提出了一种课堂教学、实验探索与自主学习相结合的教学模式。在该教学模式下，使得学生在学习中实践，在实践中学习，逐步学会主动驾驭知识，提高综合应用所学知识解决实际问题的能力。

关键词 教学模式 教学案例 科氏力 相对运动

中图分类号：G642                                    文献标识码：A    DOI：10.16400/j.cnki.kjdkx.2021.01.015

Abstract In the teaching process， taking "Coriolis force experimental system" as a teaching case， a teaching mode of combining classroom teaching， experimental exploration and autonomous learning is proposed. In this teaching mode， students can practice in learning， learn in practice， gradually learn to actively control knowledge， and improve the ability of comprehensive application of knowledge to solve practical problems.

Keywords teaching mode; teaching case; Coriolis force; relative motion

0 引言

科氏力是1835年由法国气象学家科里奥利提出的。[1][2]若以旋转体系为参照系，一个质点的直线运动往往会偏离原有方向，使质点偏离原有轨迹的力就是科里奥利力，简称科氏力。像河床的冲刷，炮弹轨道的偏转，大气环流、热带气旋、季风等的偏转和偏移都受到科氏力的影响。[3][4]

1 科氏力实验系统模型

图1所示刚性圆盘可绕定轴转动。盘上1、2 处各装一个可绕圆心轴转动的小圆盘，两盘之间套有皮带。小盘1处的同轴电机可带动小盘O1、O2转动。大盘不动时，小盘1相对大盘以角速度 r转动，同时靠摩擦力带动皮带以速度Vr相对大盘运动，此时没有变形，如图1中虚线所示。当大盘绕轴逆时针以角速度 e 缓慢转动时，若小盘转动方向与大盘同向，则皮带产生分开（外凸）变形，如图中实线所示。若小盘转动方向与大盘反向，则皮带产生靠拢（内凹）变形。

取皮带上的小段质量 m作为动点，动系固连于大盘，亦即非惯性参考系。由于牵连加速度很小， m上的牵连惯性力忽略不计。科氏惯性力主要是由坐标系的转动与物体在动坐标系中的相对运动引起的，而科氏加速度为aC= ，科氏惯性力为。大盘逆时针转动时，aC 和FIC的方向分别由图1所示。

由于受到质点质量的影响，此种方法不能精确求出科氏惯性力的理论值，但是对皮带中的科氏惯性力的有效结论是：变形部分皮带中任意质点所受的科氏惯性力都相等。

2 弹性简支梁模型的简化及计算

依据科氏力实验系统的变形及受力特征，将其简化成弹性简支梁模型。取两小电机轮轴圆心的距离即变形部分皮带的长度为简支梁总长I。

分析弹性简支梁模型的受力图2可知，弹性梁同时受到均布的科氏惯性力FIC和非均布的离心力Fe的作用。有，

其中是弹性梁到圆心的距离如图2所示。通过计算可知离心力的垂直分量沿着弹性梁也是均布的。

利用结构力学的单位载荷法可求解出此简支梁的弯矩图，如图3所示。中点的弯矩值即最大弯矩值为。

3 弹性简支板模型的简化及计算

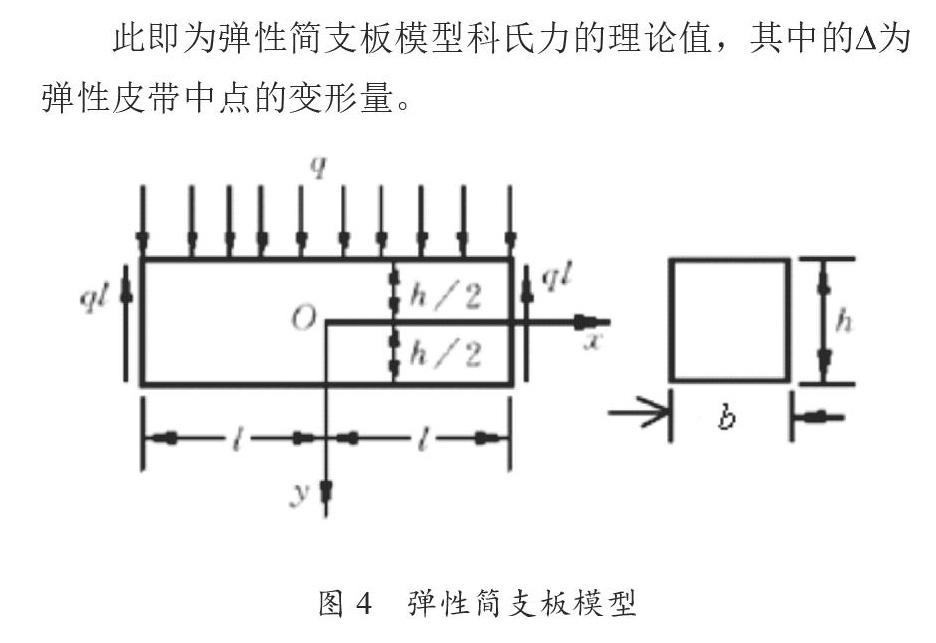
将变形部分皮带简化为弹性简支板模型，如图4所示。其中ql = FIC +Fey ，为科氏惯性力，Fey为离心力沿y轴的分量。2l为变形部分皮带的长度，h为变形部分皮带的厚度，b为变形部分皮带的宽度。由此弹性梁沿y轴方向的变形与所受的均布载荷q的关系，求出皮带中点科氏力的值。

此即为弹性简支板模型科氏力的理论值，其中的 为弹性皮带中点的变形量。

4 结论

该开放性教学模式，是以可转动圆盘皮带轮上的皮带为研究对象，以理论力学、弹性力学、结构力学知识为理论依据，以“科氏力实验系统”为联系纽带进行研究，不仅再现了科里奥利力及科氏加速度现象，而且还求出了在不同的转动关系下弹性皮带产生的变形，并用相关的数值方法解方程，从而得出变形与科氏力之间的关系。

在这一教学中，让学生亲自实践了力学建模、实验实践、理论分析、数值仿真的全过程。这一开放式的实践教学活动，使学生在科研活动、工程实践能力和创新意识等诸多方面都得到有效的训练和提高。

参考文献

[1] 贾启芬，刘习军.理论力学[M].北京：机械工业出版社，2014.

[2] 劉习军，贾启芬.振动理论及工程应用[M].北京：机械工业出版社，2017.

[3] 周松鹤，徐烈烜.工程力学[M].北京：机械工业出版社，2003：31-35.

[4] 王润富.弹性力学简明教程[M].北京：高等教育出版社，2004：113-125.